一类特殊分式线性方程的新解法

钱云

（巢湖学院，安徽 巢湖 238000）

一类特殊分式线性方程的新解法

钱云

（巢湖学院，安徽 巢湖 238000）

讨论了一类特殊类型的分式线性微分方程的求解。通过观察题设条件，给出两种较为简洁的新解法，并将其与常规解法进行了比较。

分式线性方程；变量分离方程；恰当方程

1 引言

对于分式线性微分方程

通常的解法是借助于平面上两直线的相关位置，分为三种情况加以讨论[1-3]。记

对于l1，l2重合或平行的情形，引入的变量变换简单易解；而对于l1，l2相交的情形，则需要借助于坐标轴平移公式，进行两次变量变换化为变量分离方程进行求解，计算量较大。本文将讨论此种情形下满足一定条件的特殊类型分式线性微分方程，给出较为简便的两种解法，举例给出其应用。

2 满足一定条件的两种解法

对于分式线性微分方程（1），当

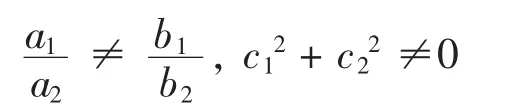
且a2＋b1=0时，我们给出两种不同的解法。

所以它是恰当方程。

3 解法实例

注 以上两种方法对于（1）中c1=c2=0的情形也有效，能起到简化计算的效果。通常对于分式线性方程，化为齐次方程，利用变量变换化为变量分离方程进行求解。若满足a2+b1=0，则可以直接引入变量变换u=a2x+b2y，化为变量分离方程，或按恰当方程方法进行求解，计算显得更方便。下面举例说明。

我们首先用常规的方法求解（解法1），再用本文给出的两种方法求解（解法2、解法3），并比较它们之间的异同。

比较上面的几种解法，可以看出，解法2、解法3计算显得更方便。

参考文献：

[1]周义仓，靳祯，秦军林.常微分方程及其应用[M].北京：科学出版社，2003.

[2]庄万.常微分方程习题集[M].济南：山东科学技术出版社，2005.

[3]丁同仁，李承治.常微分方程教程[M].北京：高等教育出版社，2003.

[4]王高雄，周之铭，朱思铭，等.常微分方程：第三版[M].北京：高等教育出版社，2006.

NEW SOLUTIONS FOR A SPECIAL FRACTIONAL LINEAR EQUATION

QIAN Yun
（Chaohu College,Chaohu Anhui 238000）

This paper discusses some new solutions for a special fractional linear ordinary differential equation,that isBy means of observing the given condition,two new concise solutions are presented and are compared with the traditional solutions.

Fractional linear differential equation；Separation of variables；Exact equation

0175.1

A

1672－2868（2016）06－0001－04

责任编辑：杨松水 校对：陈 侃

2016－10－15

安徽省级教学研究项目（项目编号：2012jyxm492）；安徽高校省级自然科学研究项目（项目编号：KJ2012A205）；巢湖学院科研启动经费项目

钱云（1964－），男，安徽庐江人。巢湖学院应用数学学院，教授。研究方向：基础数学。