基于相同数据位的SoC测试数据压缩方法

黄贵林

（巢湖学院，安徽 巢湖 238000）

基于相同数据位的SoC测试数据压缩方法

黄贵林

（巢湖学院，安徽 巢湖 238000）

随着VLSI技术的不断发展，集成电路所需的测试数据量也在不断增加，给测试带来了一系列问题，对自动测试设备(ATE)的存储容量提出了挑战，有限的带宽延长了测试数据传输时间。为此，提出了一种针对相同数据位的测试数据压缩及解压算法。数据位为全0或全1的数据块，编码压缩为仅为两位的控制位和编码位，与同类经典方案相比，实验表明该方案有效提高了测试数据压缩率，平均压缩率达到63.58%，且编码算法简单。

数据块；测试数据；压缩；无关位

1 引言

“芯片内集成的晶体管数目每18个月将增加一倍”[1]，集成电路在按照摩尔定律这个规律在发展。工作频率的提高和单个芯片的集成度的不断提高，给测试提出新的要求，包括数量巨大的测试数据是测试首先需要解决的问题，并且呈不断发展的态势。与此同时，ATE的存储容量有限和传输带宽有限，使得测试成本也在不断提高，也延长了测试时间，测试数据压缩能在一定程度上解决上述问题。

目前经典的测试数据压缩方法有很多，总的来说可以分为三种[2]：编码压缩方法、基于广播扫描的压缩方法[3－4]、基于LFSR结构的压缩方法[5－6]。其中，编码压缩是一种广泛使用的测试数据压缩方案，根据数据块与编码位的一一对应的关系对数据块进行编码压缩,如：Golomb码[7]、FDR码[8]、ALT-FDR[9]、EFDR[10]、RL-HC[11]、9C[12]、BM[13]和交替与连续长度码[14]等。哈弗曼[15－17]编码也属于编码压缩，它是一种高效的静态编码方法，所得到的平均编码长度最短，但随着参与编码压缩数据块的增加，其解压结构复杂程度呈指数级增长，为此提出了SHC[18]、OSHC[19]，它们都是基于Huffman的测试数据压缩算法。OSHC和SHC将出现频率高的数据块进行Huffman编码，出现频率低的数据块不参与Huffman编码，并利用控制位和地址位进行共享编码。

本文考虑测试集中大量存在的全0或全1数据块，充分发掘测试集当中具有这种特性的数据块，能够将其编码为长度只有两位的控制位和控制位。测试集当中存在的大量无关位，可以随意填充，大量数据块可以填充为全0数据块或全1数据块，为本文方案的使用提供了理论依据。

2 本文思想

2.1 相同数据位

定义：对于每个集成电路的测试集，是由若干条测试向量构成，每条测试向量，是由若干测试位构成，而且每条测试向量的位数相同。测试集包含若干条测试向量，每条测试向量拥有大量的无关位x，在实际测试时，该无关位可以设定为0，也可以设定为1。除了无关位x，其他测试位均由由0或者1组成，而且1和0的分布具有连续分布的特点。测试向量当中，存在大量的连续的0，或者连续的1，这些连续的0或1，称为相同数据位。另外，无关位x可以设定为0或者1，提高了相同数据位的存在的可能性，提高了后续编码效率。

2.2 编码方法

设定变量数据块长度bl，按照bl将测试集划分成bl个长度相同的数据块。在划分的过程当中，测试向量可能出现不能等长划分的情况，最后一个数据块长度可能小于bl，为此在测试向量即最后一个数据块末尾添加若干个无关位X，使划分得到的数据块等长。压缩是以数据块为单位进行压缩的，每一个数据块压缩后是由两个部分构成的，压缩后的数据分为两个部分控制位和编码位。控制位为1位，编码位为1，或为0，或为原始测试数据块。

（1）划分数据块。

（2）填充无关位。

如果数据块当中，只含有1和无关位x，则将其填充为1；

如果数据块当中，只含有0和无关位x，则将其填充为0；

如果数据块当中，既含有0，也含有1，对于数据块当中的x，可填充为1，也可填充为0；

（3）编码，压缩数据块，编码得到数据控制位和编码位。

填充得到的数据块当中，只有1或者0。

如果数据块为全0数据块，则编码压缩得到的数据为00，第一个0为控制位，第二个0为编码位，表示全0数据块；

如果数据块为全1数据块，则编码压缩得到的数据为01，第一个0为控制位，第二个1为编码位，表示全1数据块；

如果数据块为非全0或非全1数据块，则编码压缩得到的数据为控制位1+原始数据块；

2.3 编码算法

pattern_number和pattern_length分别为测试集的测试向量个数和测试向量长度。

将每条测试向量，划分成bn个数据块，且长度相等为bl。

bn=(pattern_length+bl-1)/bl。

bit[i][j][k]为第i(0≤i≤pattern_number-1)个测试向量的第j(0≤j≤bn-1)个数据块的第k(0≤k≤bl-1)位。

（1）初始化i=0；

（2）初始化j=0；

（3）初始化k=0；

（4）for（i=0；i＜pattern_number；i++）

（5）for(j=0；j＜bn；j++)

（6）{

（7） for（k=0；k＜bl；k++）

（8） 如果bit[i][j][k]为全0，则数据块bit[i][j]压缩为00；

（9） for（k=0；k＜bl；k++）

（10） 如果bit[i][j][k]为全1，则数据块bit[i][j]压缩为01；

（11）否则，则数据块bit[i][j]压缩为1+数据块bit[i][j]；

（12）}

2.4 编码实例

对于实例测试向量，将其划分成如表1所示的等长的长度为6的7个数据块，其中x为无关位，在测试过程中，可以将其设定为1或为0。数据块0000xx，可以设定为全0数据块，数据块1xx111，可以设定为全1数据块。对于全0数据块或全1数据块，可以将其压缩为控制位0和编码位0或者1。因此数据块0000xx压缩为00，1xx111压缩为01。同理，数据块111111、数据块000000，编码位为01、00，压缩后的数据由控制位和编码位构成。

对于数据块010101、数据块01x10x为非全0或全1数据块，不能按照上述情况进行压缩，采用特殊方法进行处理，得到控制位置1，编码位为被压缩数据块本身。

综上所述，测试向量0000xx1xx11111111100 000010101001010101x10x，压缩为0001010011010101010101101x10x，由42位压缩为29，其中x可为1，也可为0。

表1 编码实例

3 解码体系结构及原理

本方案的解压体系结构主要是由FSM和计数器构成，如图1所示，‘enb’是输入使能信号，‘data_in’接收压缩后的测试数据。‘flag’为MUX的通道选择信号。‘dcr’用于计数器减1，‘rt’用于指示计数器的复位0状态,计数器计数范围为编码数据块长度。

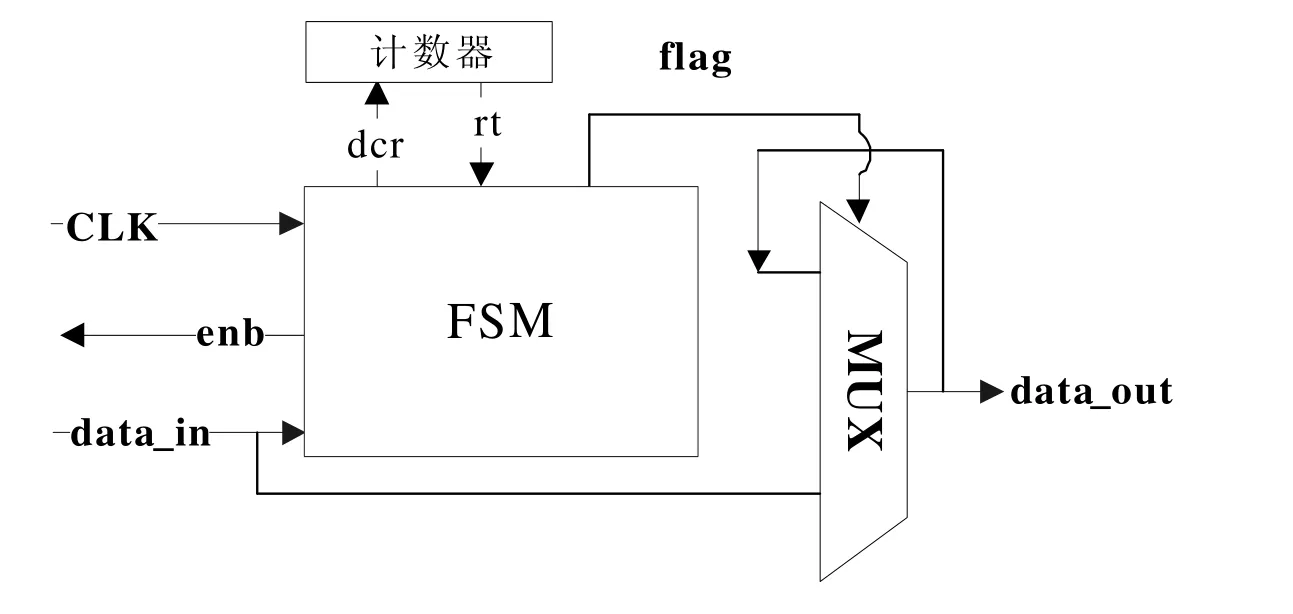
图1 测试解压结构

（1）若‘data_in’为低，解压全0或全1数据块压缩数据。则‘enb’为高，则‘flag’为低，‘flag’选通data_in当中的数据进入MUX，解码得到全0或全1数据块第1个测试数据位，进入被测电路。然后，‘flag’为高，‘flag’选通data_out当中的数据0或1进入MUX，继续成为data_out，获得与第1个数据位相同的后续测试数据位。data_out当中的测试位，反复作为MUX的输入。直至‘rt’为高，‘enb’为低，解码获得整个数据块的全0或全1测试数据位。

（2）若‘data_in’为高，解压非全0或全1数据块压缩数据。则‘enb’为高，则‘flag’为低，‘flag’选通data_in当中的数据进入MUX，解码得到非全0或全1数据块第1个测试数据位，进入被测电路。然后，‘flag’继续为低，‘flag’ 继续选通data_in当中的数据进入MUX，获得非全0或全1数据块的后续数据位。直至‘rt’为高，‘enb’为低，解码得到整个非全0或全1数据块。

与图1所示FSM相对应的有限状态机的状态转换图，如图2所示，它包含S0、S1、S2、S3等4个状态。S0～S1是接受控制位，S1～S2是接受编码位，S2的循环是得到与编码位相同的数据块后续测试位。S0～S3是接受控制位，S3的循环是从data_in中直接接收数据块后续测试位，作为解压得到的测试位。

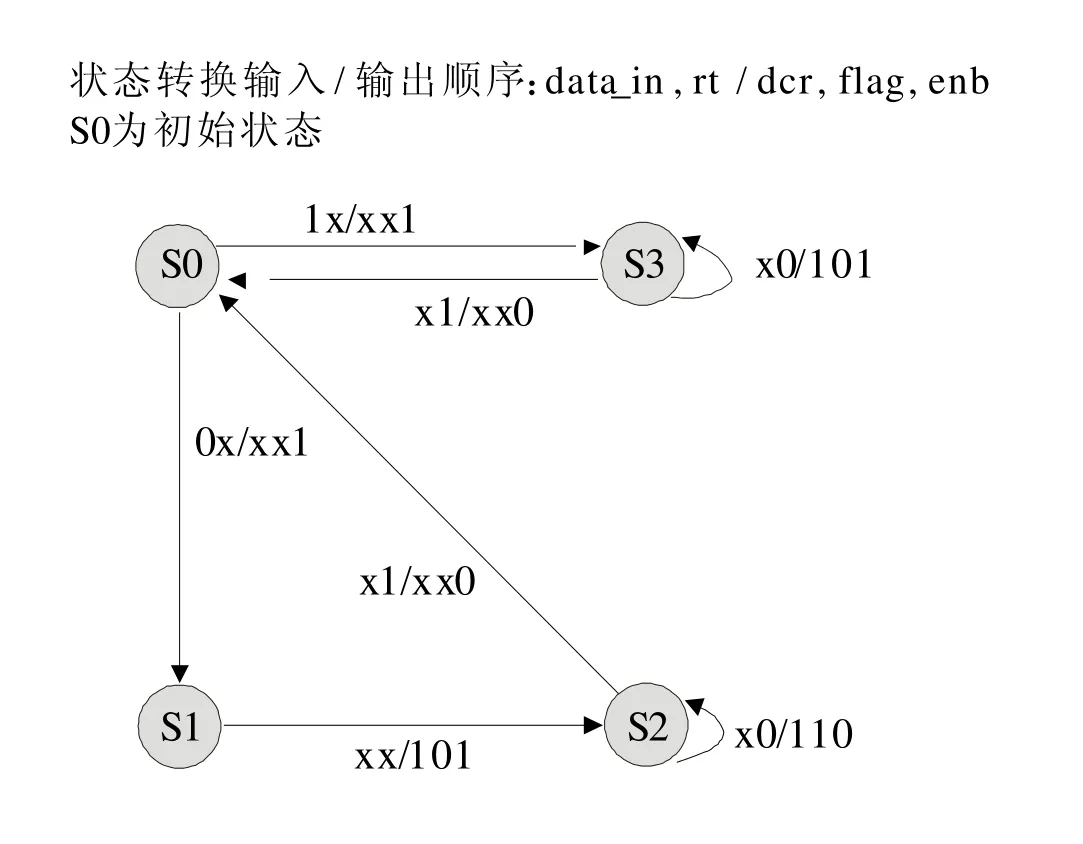
图2FSM状态转换图

4 实验结果

为客观说明本文算法的实践意义,采用Visual C++作为实验工具, 选用并压缩6个ISCAS’89标准电路的测试集。实验结果如表2所示，表中所有数据都为压缩率，第12列为采用本文方案的压缩效果，并与BM、9C、RL-HC、EFDR、ALT-FDR、FDR、GOLOMB、VIHC、SHC、OSHC等经典压缩方案进行对比。第8行、第12列为平均压缩率63.58%，都高于其他绝大数方案的压缩率。

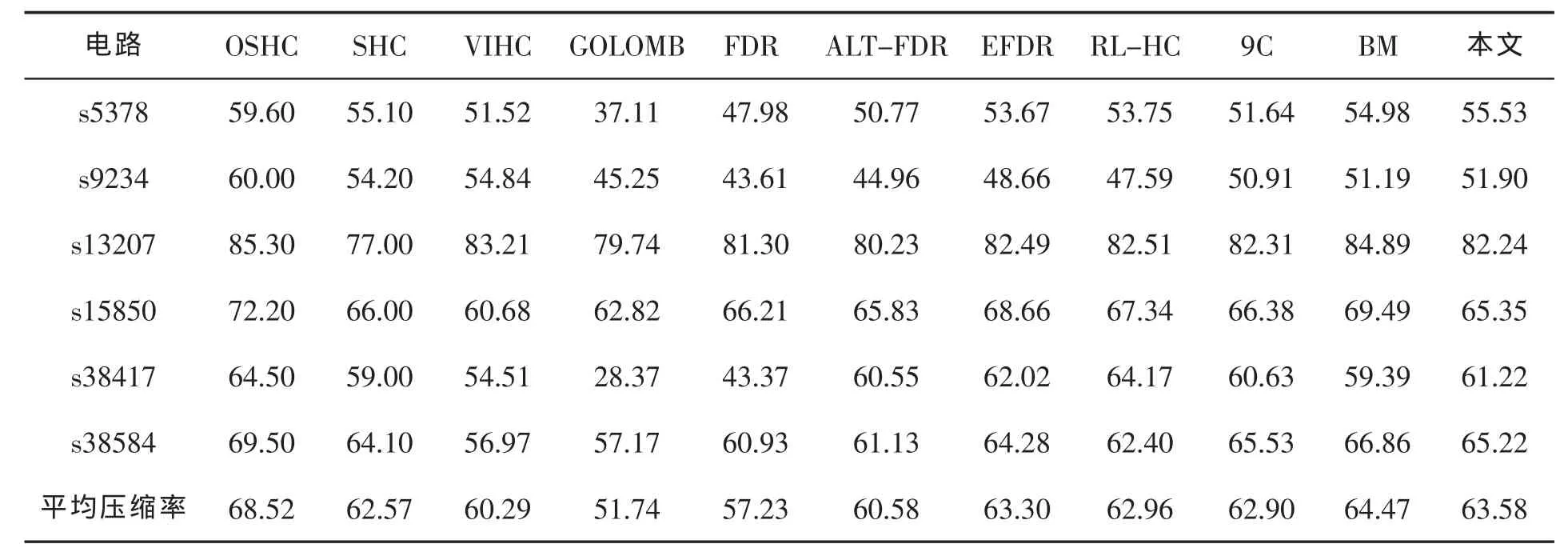
表2 实验结果

5 结论

本文利用测试集当中大量存在连续的测试位0或者大量存在的连续的测试位1这种特征。将其压缩成一位控制位和一位测试位，为本文方案压缩奠定了重要基础和提供了可能。与同类方案相比，具有较高的测试数据压缩率，且压缩的对象为定长的测试数据块，在一定程度上，简化了测试过程中的数据解压过程。

[1]MOORE G.Progress in digital integrated electronics[C].Proceedings of International Electron Device Meeting（IEDM）Teeh.Digest，1975:11-13.

[2]TOUBA N A.Survey of test vector compression techniques[J].IEEE Des.Test Comput.,2006，（4）:294-303.

[3]MITRA S，Kim K S.XPAND:An efficient test stimulus compression technique[J].IEEE Trans.Compute rs,2006，（2）:163-173.

[4]俞洋，彭喜元，张毅刚.基于重复子向量的测试数据压缩算法[J].仪器仪表学报，2009，（2）:356-361.

[5]KOENEMANN B.LFSR-coded test patterns for scan designs[C].Proceedings of European Test Conference,Munich,Germany,1991:237-242.

[6]YI M X，LIANG H G，ZHAN K H，et al.Optimal LFSR-Coding test data compression based on test cube dividing[C].Proceeding of International Conference on Computational Science and Engineering（CSE 2009），2009:698-702.

[7]ANSHUMAN C，KRISHNENDU C.Test data compression and decompression based on internal scan chains and golomb coding[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2002，（6）:715-722.

[8]ANSHUMAN C，KRISHNENDU C.Test data compression and test resource partitioning for system-on-a-chip using fre－quency-directed run-length（FDR）codes[J].IEEE Transactions on Computers,2003，（8）:1076-1088.

[9]CHANDRA A，CHAKRABARTY K.A unified approach to reduce SoC test data volume,scan power and testing time[J].IEEE Trans.Computer-Aided Design Integrated Circuits Syst.,2003，（3）:352-363.

[10]El-MALEH A H，Al-ABAJI R H.Extended frequency-directed run length code with improved application to system-ona-chip test data compression[C].in Proc.9th IEEE Int.Conf.Electron.,Circuits Syst.,2002:449－452.

[11]NOURANI M，TEHRANIPOUR M.RL-Huffman encoding for test compression and power reduction in scan application[J].ACM Trans.Des.Autom.Electron.Syst.,2005，（1）:91－115.

[12]TEHRANIPOOR M，NOURANI M K.Nine-Coded compression technique for testing embeddedCores in SoCs[J].IEEE Trans.VLSI Systems,2005，（6）:719-731.

[13]El-MALEH A H.Efficient test compression technique based on block merging[J].IET Comput.Digit.Tech.,2008，（5）:327－335.

[14]梁华国，蒋翠云.基于交替与连续长度码的有效测试数据压缩和解压[J].计算机学报，2004，（4）:549-554.

[15]GONCIARI P T，Al-HASHIMI B，NICOLICI N.Improving compression ratio,area overhead,and test application time for system-on-a-chip test data compression/decompression[C].in Proc.Design Automation Test in Europe,Paris,France,2002: 604-611.

[16]欧阳一鸣，邹宝升，梁华国，等.基于部分游程翻转的SoC测试数据压缩[J].电子测量与仪器学报，2010，（1）:23-28.

[18]JAS A，GHOSH-DASTIDAR J，NG M E，et al.An efficient test vector compression scheme using selective huffman coding[J].IEEE Trans.Computer-Aided Design of Integrated Circuits and Systems,2003，（6）:797-806.

[19]KAVOUSIANOS X，KALLIGEROS E，NIKOLOS D.Optimal selective huffman coding for test-data compression[J].IEEE Trans.Computers,2007，（8）:1146-1152.

A STUDY ON THE TEST DATA COMPRESSION METHODS OF SYSTEM-ON-CHIP（SOC）BASED ON THE SAME TEST DATA BITS

HUANG Gui-lin
（Chaohu College,Chaohu Anhui 238000）

With the continuous development of very large scale integration（VLSI）,the amount of test data required by integrated circuits is increasing,which causes a series of problems to test,and brings great challenges to the storage capacity of automatic test equipment（ATE）.The limited bandwidth of ATE lengthens the transmission time of test data.Therefore,a new algorithm of test data compression/decompression is proposed based on the same bits of test data.For the data block whose data bits are all 1 or 0,the code is compressed into only two-bit control bit and two-bit encoding bit.Compared with the other classical ways,the experimental results shows that this way effectively improved the compression ratio whose average ratio increases by 63.58%,and the encoding algorithm is simpler.

Data block；Test data；Compression；Independent bit

TP302

A

1672－2868（2016）06－0015－05

责任编辑：杨松水 校对：陈 侃

2016－10－08

巢湖学院校级科研资助项目（项目编号：XLY-201409）；安徽省省级教学研究项目（项目编号：2014jyxm331）；安徽省省级特色专业计算机科学与技术省级特色专业（项目编号：2013tszy020）；安徽省高校省级教学团队（项目编号：2016jxtd083）

黄贵林（1985－），男，安徽望江人。巢湖学院信息工程学院，助教。研究方向：片上系统与片上网络的综合与测试。