一般混合微分系统第二特征值的上界估计

卢亦平，钱椿林

(苏州市职业大学 数理部，江苏 苏州 215104)

一般混合微分系统第二特征值的上界估计

卢亦平，钱椿林

(苏州市职业大学 数理部，江苏 苏州 215104)

考虑一般混合微分系统第二特征值的上界估计.利用试验函数、分部积分和不等式等估计方法与技巧，获得用第一特征值来估计第二特征值的上界的不等式，其估计系数与区间的度量无关.其结果在常微分方程的研究和应用中起着重要的作用.

一般混合微分系统；特征值；特征函数向量；上界

1 主要结果

设a b,( )⊂R是一个有界区间，考虑如下一般混合微分系统的特征值估计问题.

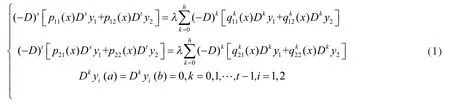
ij ij ji ijqx qx

k() ()= ，i，j=1，2，k=0，1，…h；2≤k＜s≤t，为正整数.设任意的

k

ij ji

ξ =[ ]

ξξ

12T，满足

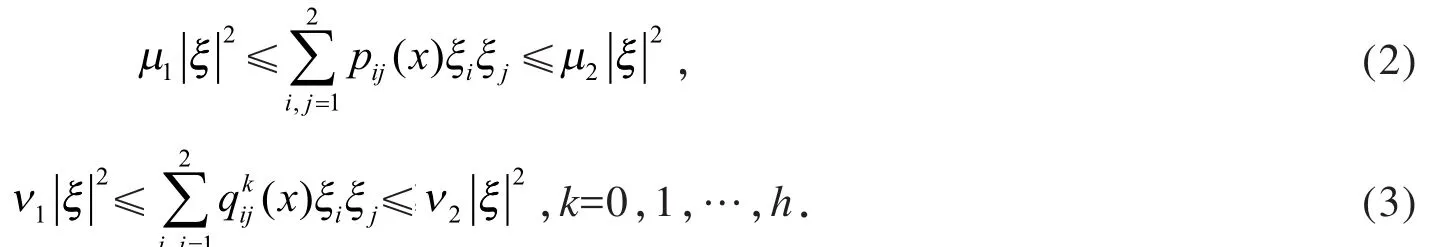
式中μ1，μ2，v1，v2为正实数.

把问题(1)写成矩阵形式，设

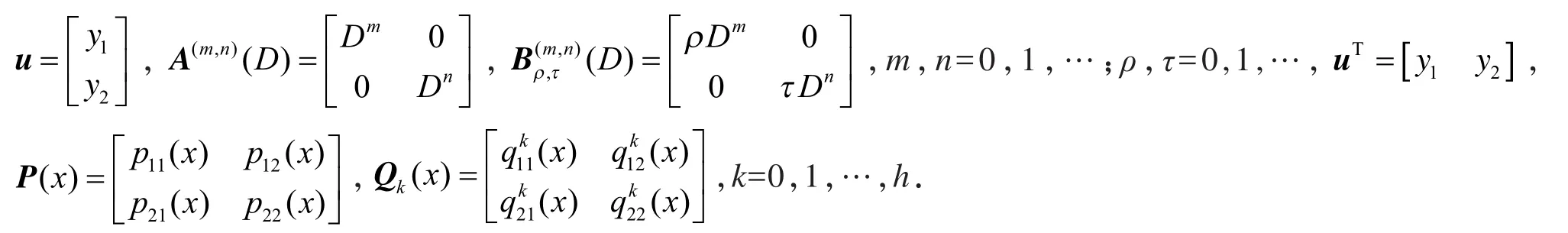
则问题(1)化为如下等价的矩阵形式

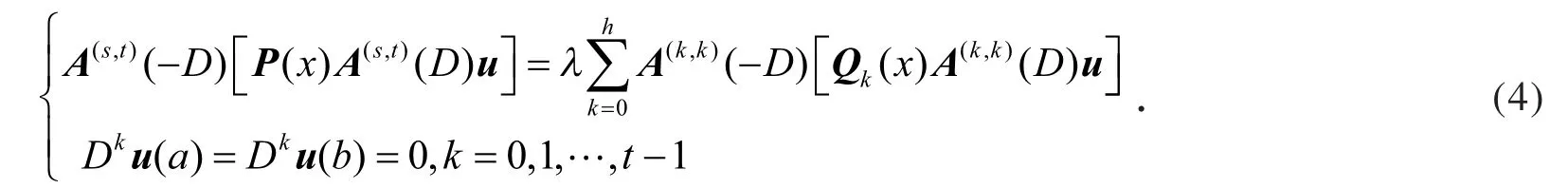
微分方程的特征值估计已有结果[2-5]，相同阶微分系统特征值估计也有结果[6-8].在本文中，考虑一般混合微分系统的问题，将文献[6]~文献[8]推广到不同阶的微分方程组成的方程组的情形.运用文献[9]中的方法，对于问题(1)获得了用第一特征值来估计第二特征值的上界的不等式，其估计系数与区间的度量无关.其结果在物理学和力学中有着广泛的应用，在常微分方程的研究中起着重要的作用.

定理设λ1，λ2分别是问题(1)的第一、第二特征值，且0<λ1≤λ2，n=1，2，…，h，则有() ()= = (k=0，1，…，h)，得到文献[1]中的式(5)、式(6)，所以文献[1]的结果是本文中的一个特例.且本文结果比文献[1]更优，即

注1取px px

12 21 0

() ()= =，qx qx

12 21 0

k k

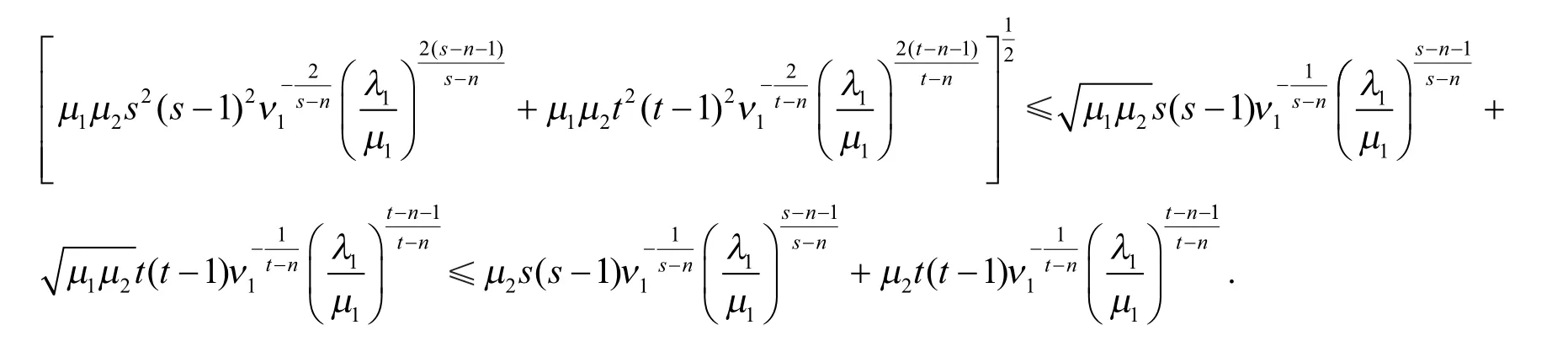
注2适当选取正整数n使得式(5)和式(6)的左端达到最小.

2 定理的证明

设λ1是问题(4)的第一特征值，相应于λ1的特征向量函数为u1，简记u=u1，且满足

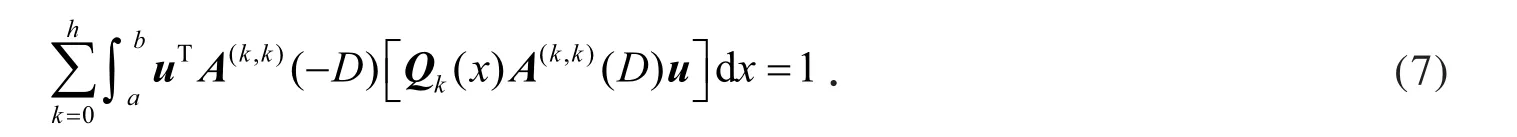
利用分部积分和式(7)，得

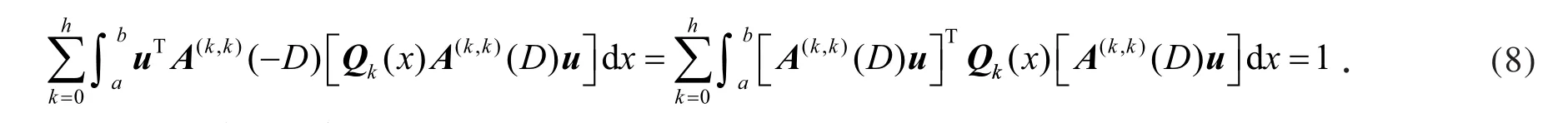
利用分部积分和式(8)，有

利用式(2)和式(9)，得

利用式(10)，有

利用式(3)和式(8)，得

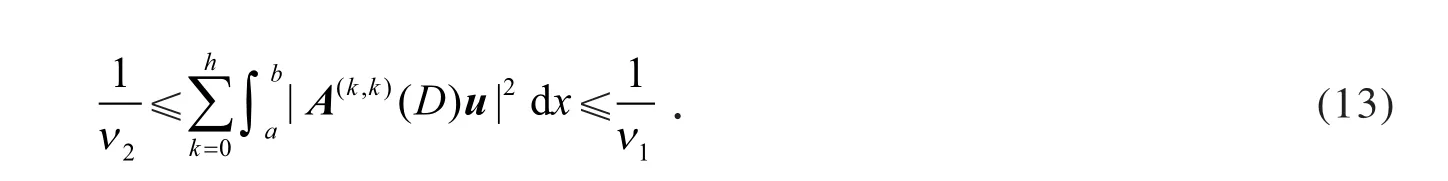
利用式(13)，有

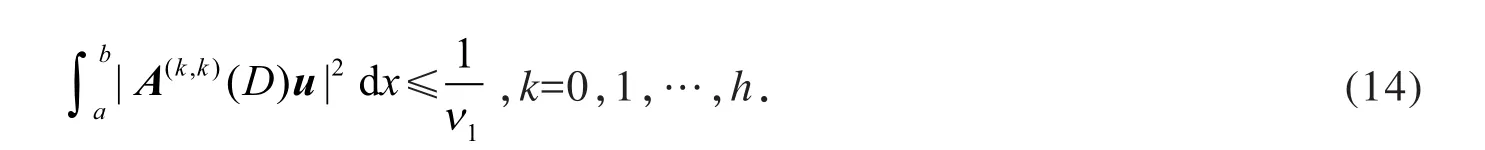
利用式(14)，得

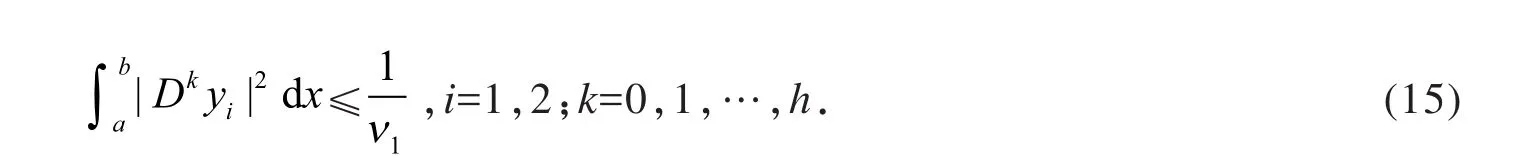
设φ () ( )

x x g= - u，

利用分部积分，直接计算得

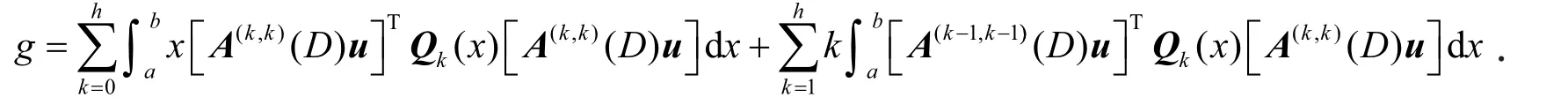
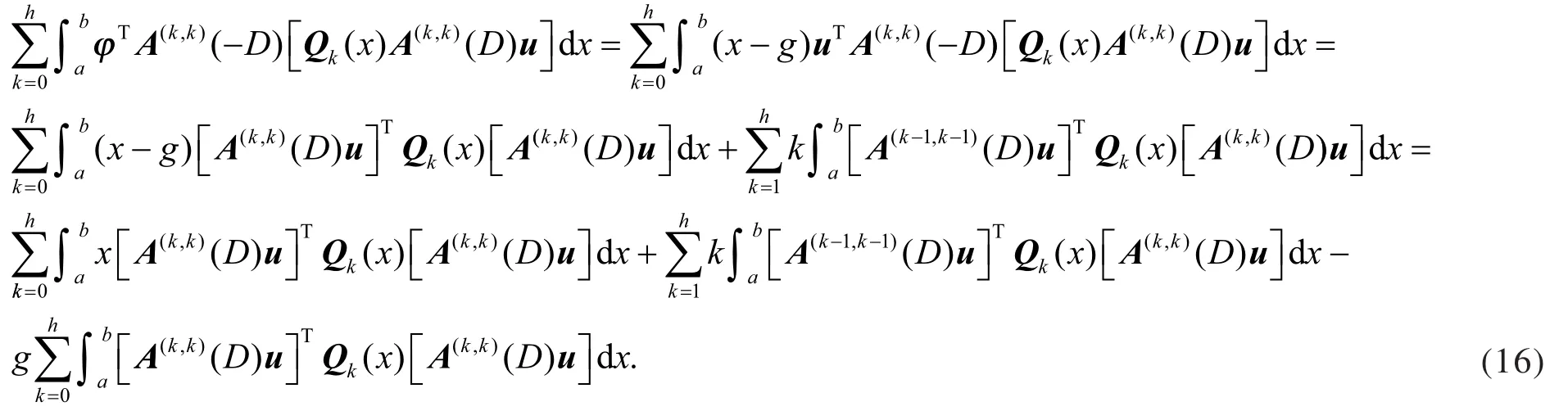
，式(16)等于0，即

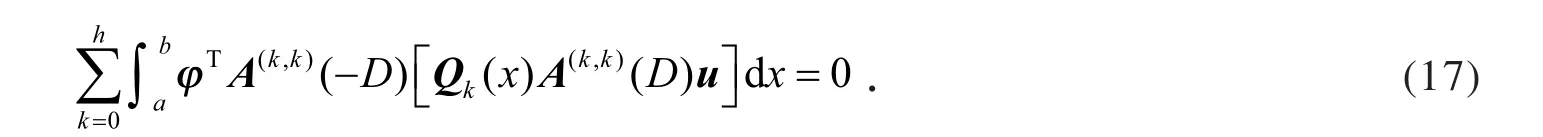
由式(17)知，φ与u广义正交，且满足

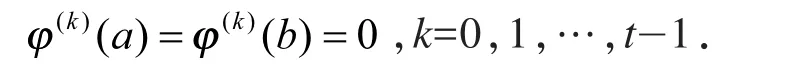
利用Rayleigh定理，则下列不等式成立

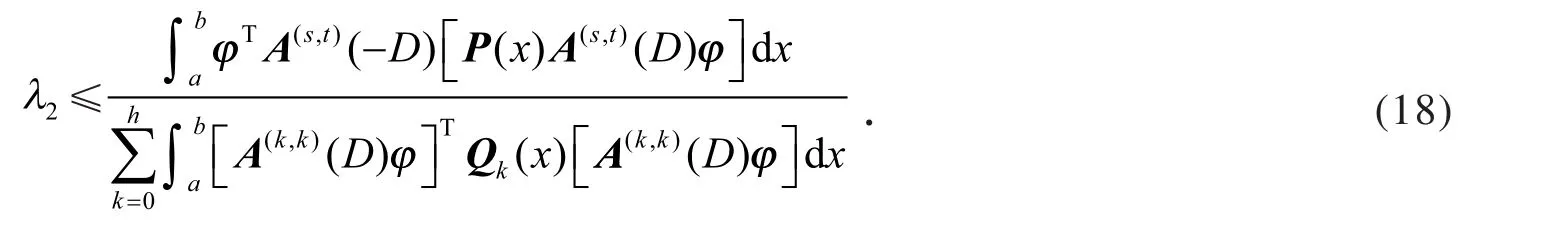
计算得

利用分部积分和φ () ( )

x x g= - u，有

即有

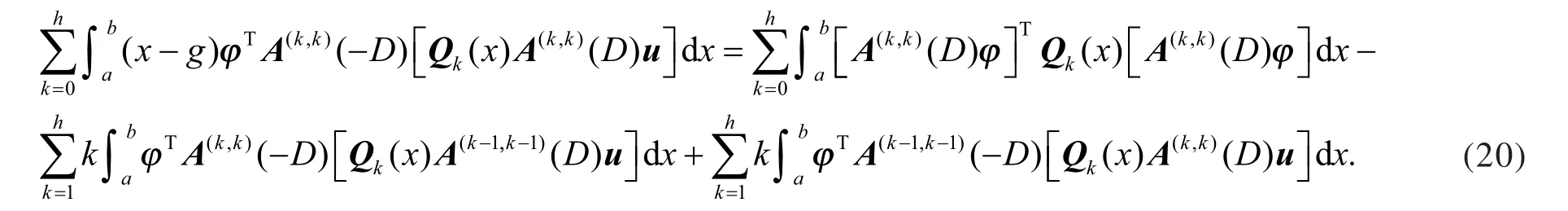
结合式(19)和式(20)，得

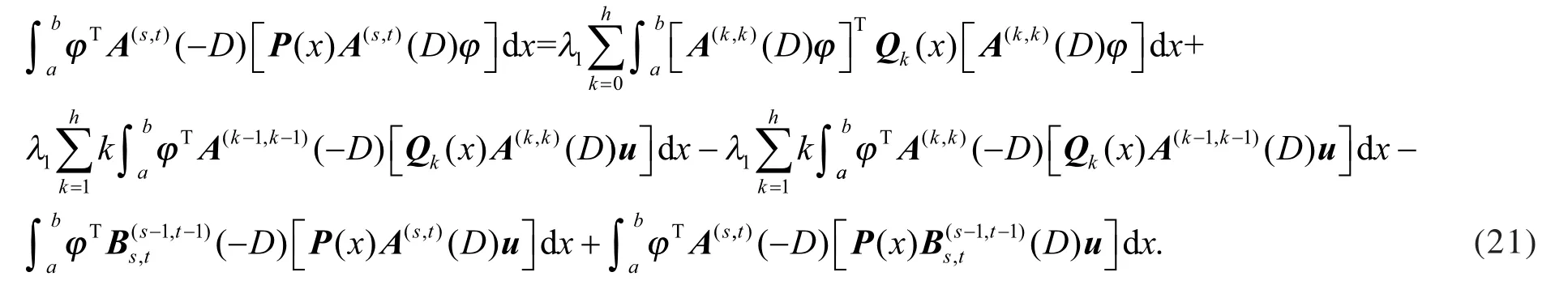
假设

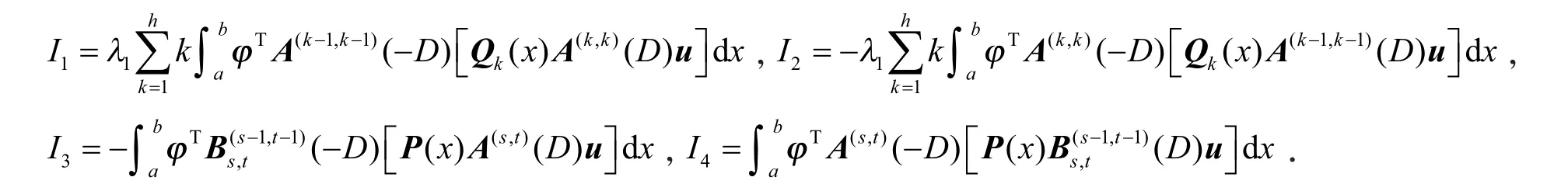
利用式(21)，有

利用式(18)和式(22)，有

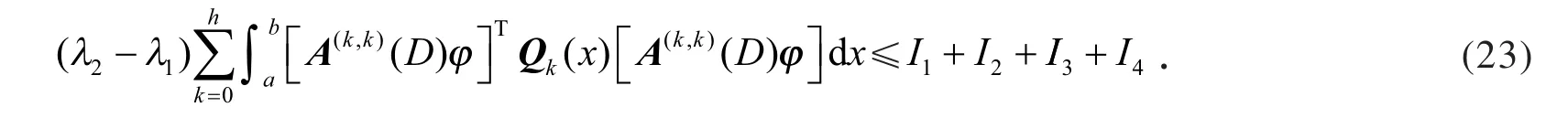
引理1设y是问题(4)所对应第一特征值λ1的特征向量函数u的某一分量，n=0，1，…，h，则

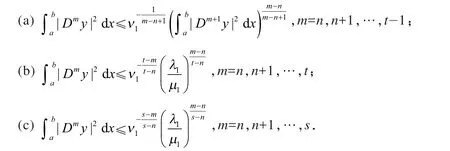
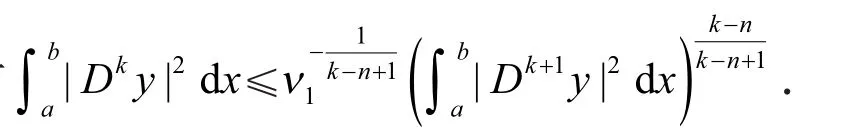
当m=k+1时，利用分部积分、Schwarz 不等式和归纳假设，得

一种基于CCBⅡ空气系统的机车受电弓气动控制失效分析与处置…………肖洪江 王自强 刘海军 (3-46)

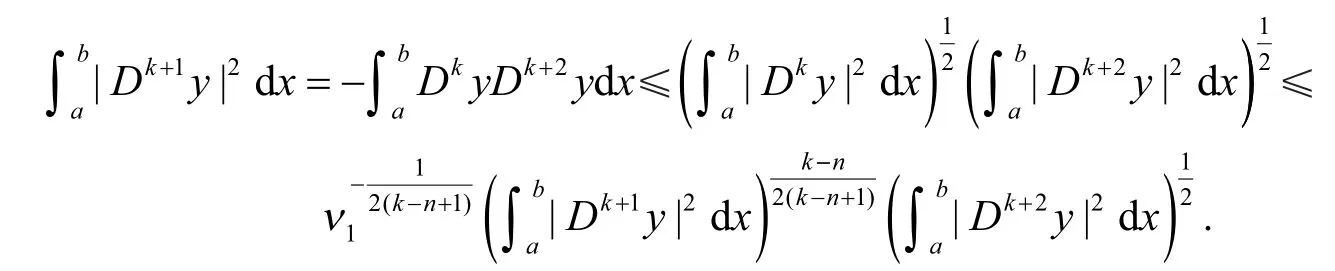
化简整理，得

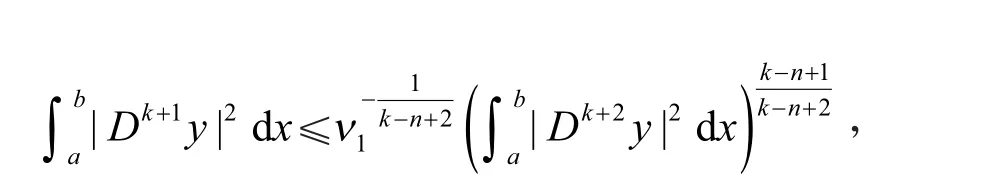
即引理1(a)成立.

对于(b)，反复运用引理1(a)和式(11)，得

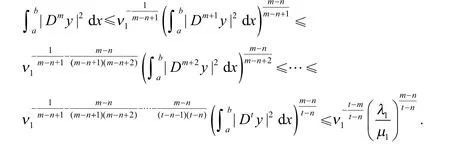
即得引理1(b)成立.对于(c)，类似地，利用证明引理1(b)的方法和式(11)，同样可得引理1(c)成立.

引理2设u是问题(4)所对应第一特征值λ1的特征向量函数，则，

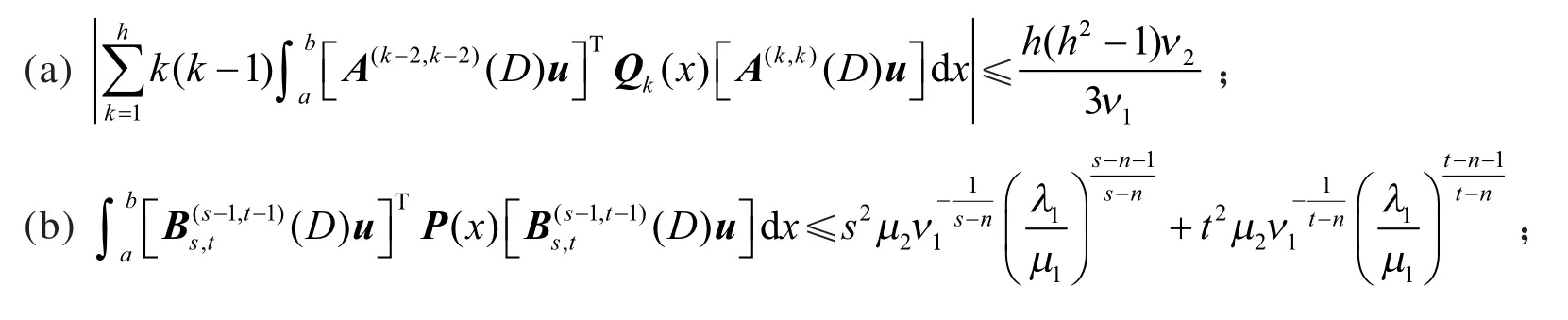
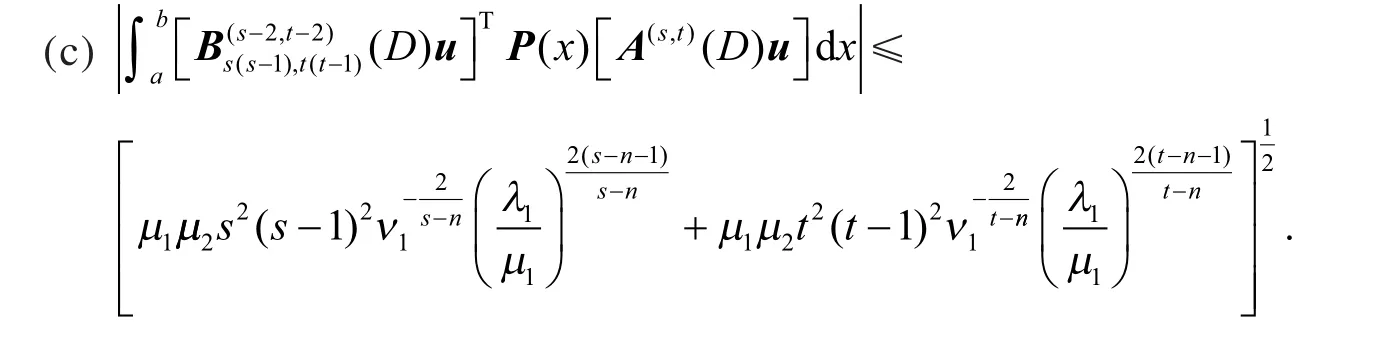
证对于(a)，利用式(3)和式(14)，得

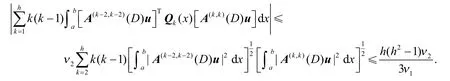
对于(b)，利用式(2)、引理1(b)和引理1(c)，得

对于(c)，利用式(2)，Schwarz 不等式、引理1(b) 和引理1(c)，得

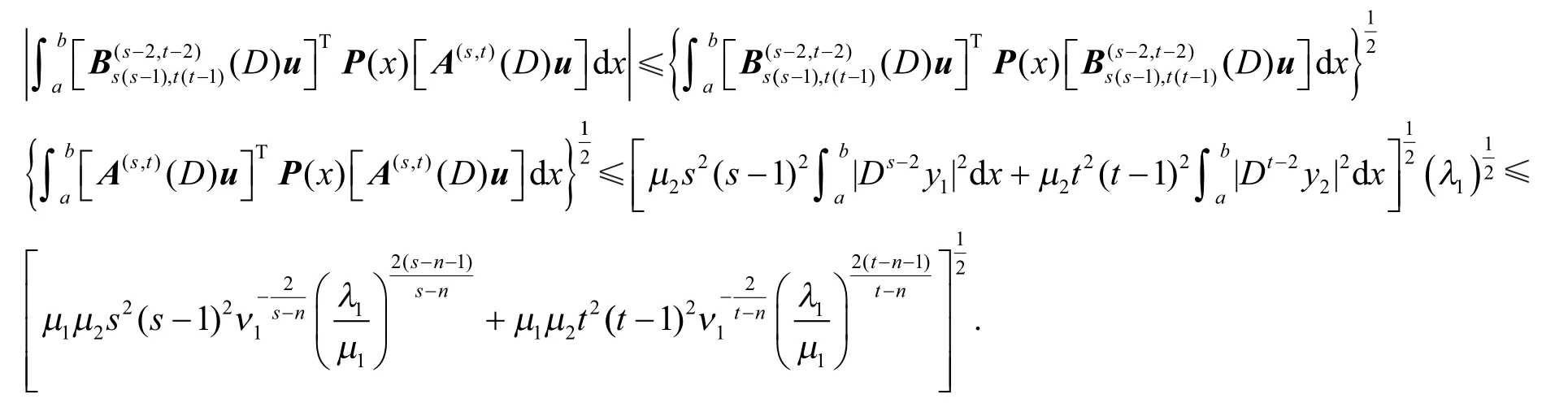
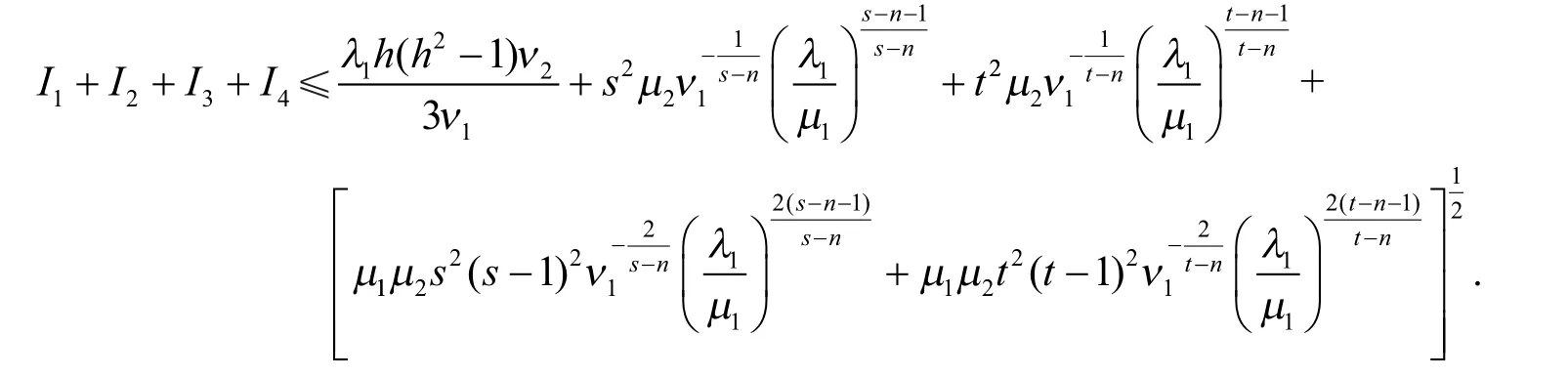
证利用分部积分和φ () ( )

x x g= - u，得

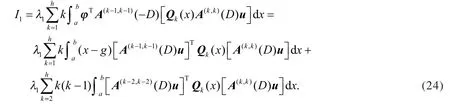
类似地，可以得到

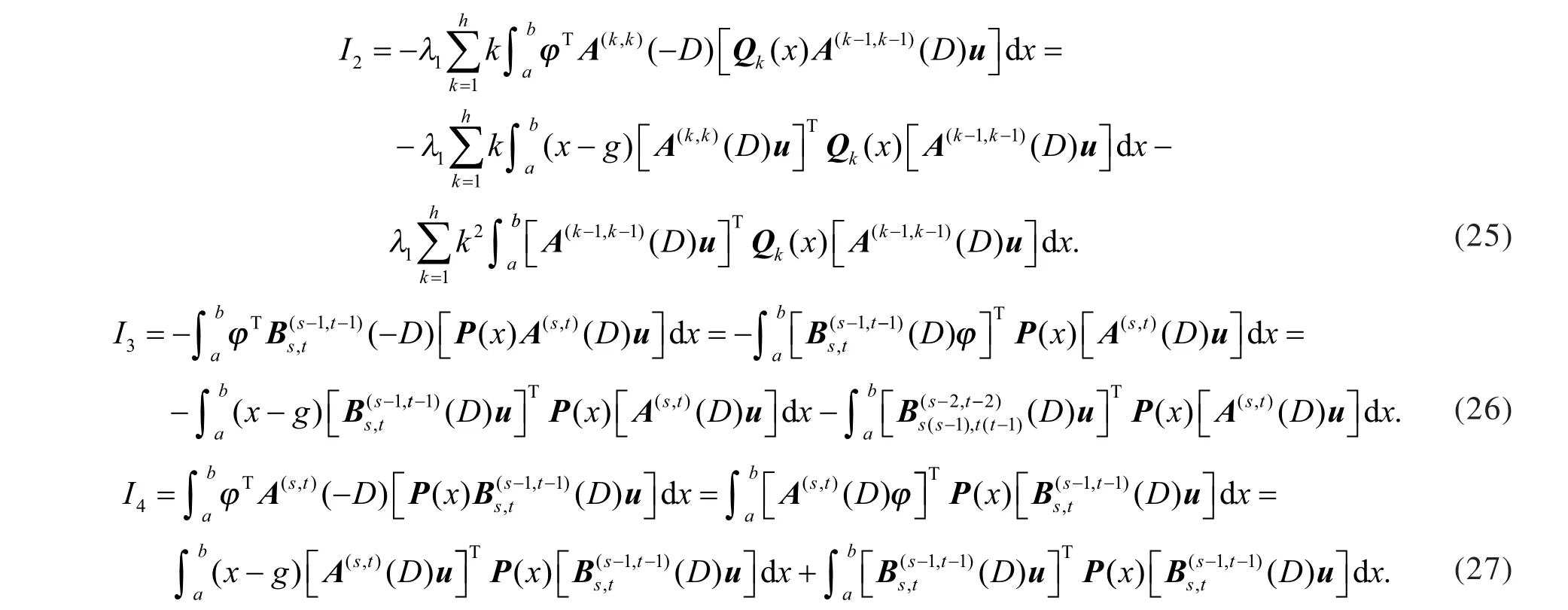
利用式(24)、式(25)、式(26)和式(27)，得

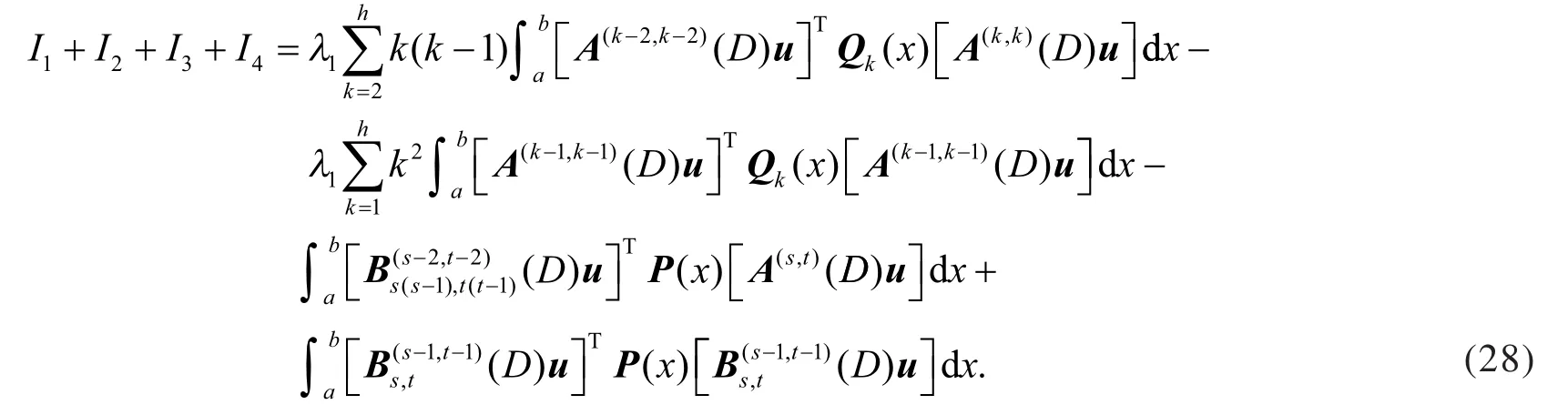
利用式(28)和引理2，得

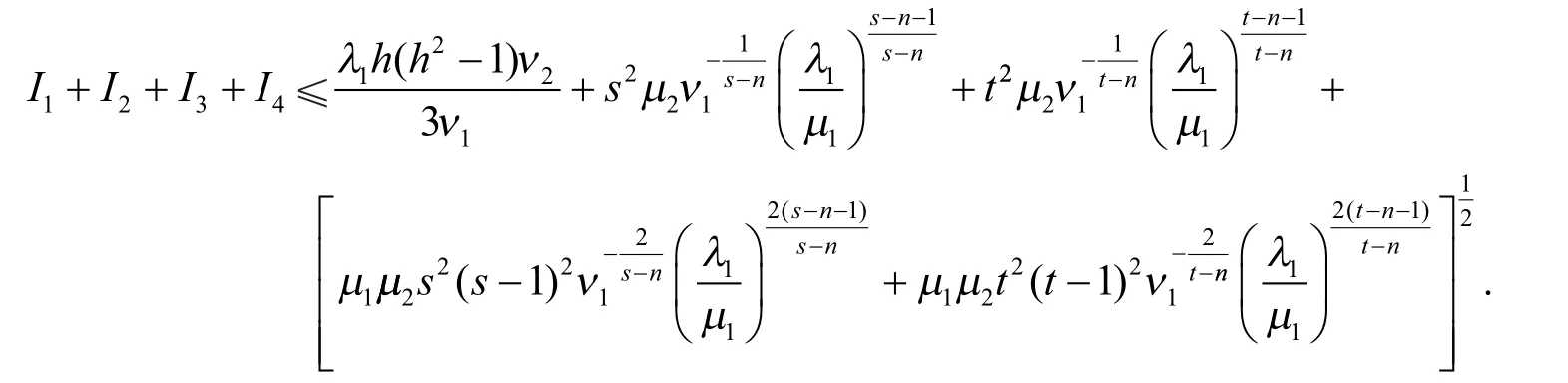
引理4对于φ与λ1，有

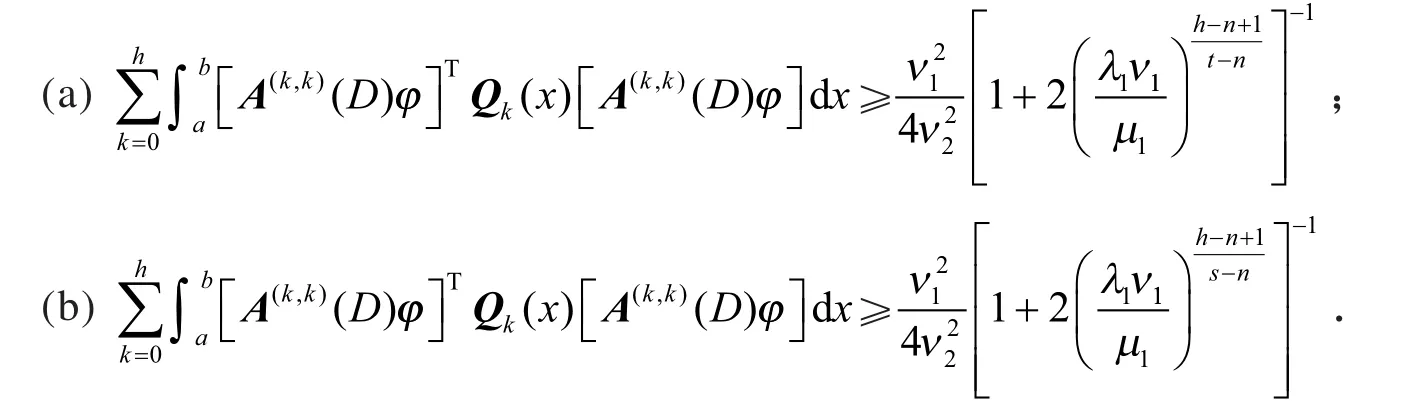
证利用分部积分和φ () ( )

x x g= - u，得

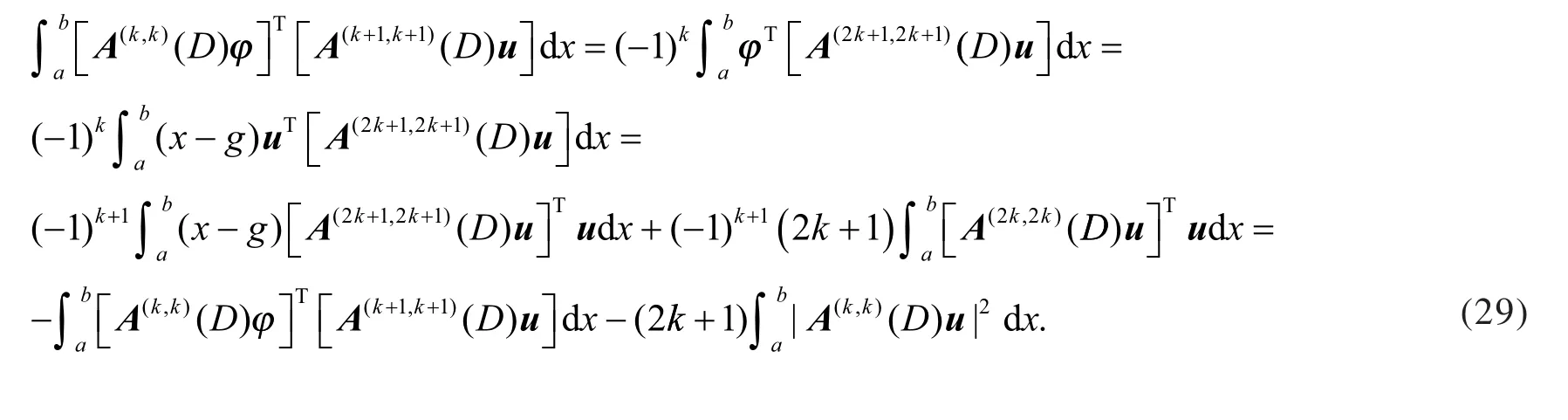
利用式(29)，得

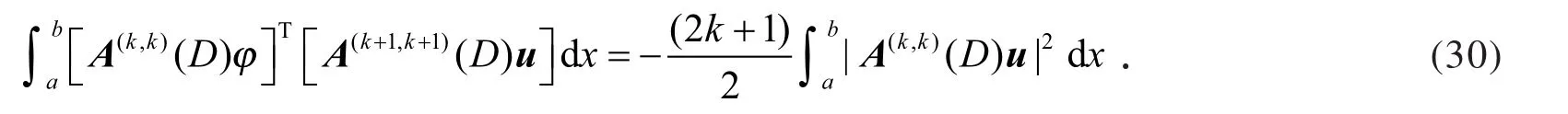
利用式(30)，得

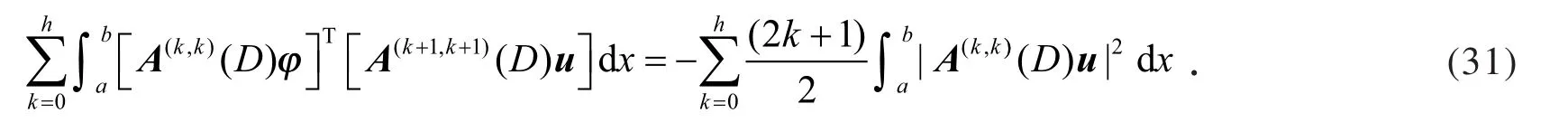
利用式(3)和式(13)，得

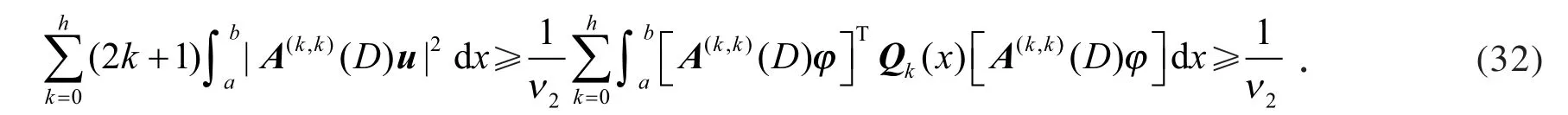
利用式(31)、式(32)、式(3)、式(13)、引理1(b)和Schwarz 不等式，得

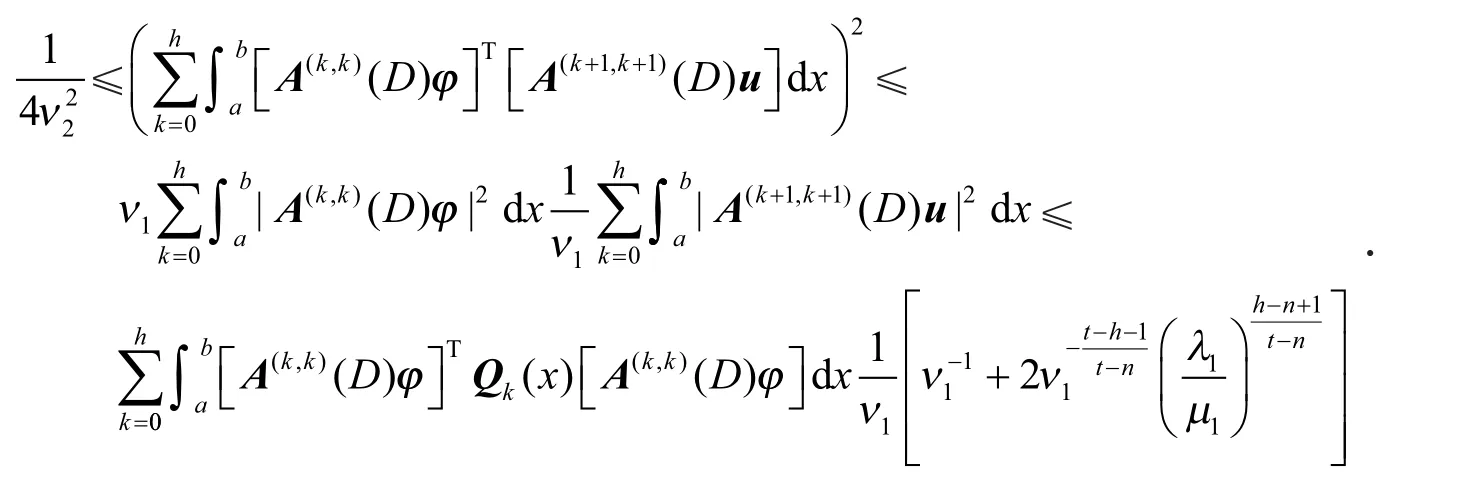
整理可得引理4(a)成立.类似地，利用引理1(c)和上述方法，同样可得引理4(b)成立.

定理的证明：利用引理3、引理4(a)和式(23)，得到定理的式(5).利用引理3、引理4(b)和式(23)，得到定理的式(6).

[1] 卢亦平，钱椿林.混合微分系统带权第二特征值的上界[J].长春大学学报(自然科学版)，2014，24 (10)：1364-1369.

[2] 卢亦平，钱椿林.多项式微分算子带一般权第二特征值的上界估计 [J].长春大学学报(自然科学版)，2014，24 (2)：175-179.

[3] 卢亦平，钱椿林.任意阶微分算子带一般权第二特征值的上界估计[J].长春大学学报(自然科学版)，2012，22 (12)：1490-1494.

[4] 卢亦平，钱椿林.高阶微分算子带权的第二特征值的上界估计[J].长春大学学报(自然科学版)，2010，20 (6)：4-7.

[5] 卢亦平，钱椿林.微分方程带一般权的第二特征值的上界估计[J].长春大学学报(自然科学版)，2009，19 (10)：7-9.

[6] 朱敏峰，钱椿林.正则任意阶微分系统带一般权第二特征值的上界[J].长春大学学报(自然科学版)，2013，23 (8)：971-980.

[7] 朱敏峰，钱椿林.正则高阶微分系统带权第二特征值的上界[J].苏州市职业大学学报，2012，23(4)：30-36.

[8] 陈卫忠，钱椿林.正则微分系统带权第二特征值的上界[J].常熟理工学院学报，2010 (10)：38-42.

[9] HILE G N，YEN R Z.Inequalities for eigenvalue of the biharmonic operator[J].Pacifc J.Math.1984 (1)：115-133.

[10] PROTTER M H.Can one hear the shape of a drum? [J]. SIAM Rev.，1987 (2)：185-197.

(责任编辑：沈凤英)

Estimate of the Upper Bound of Second Eigenvalue for General Mixed Differential System

LU Yi-ping，QIAN Chun-lin
(Department of Mathematics and Physics，Suzhou Vocational University，Suzhou 215104，China)

This paper considers the estimate of the upper bound of second eigenvalue for general mixed differential system.The upper of second eigenvalue is dependent on the first eigenvalue by using integral and inequality estimation.The estimate coeffcients do not depend on the measure of the domain in which the problem is concerned.This kind of problem is significant both in theory of differential equations and in application to mechanics and physics.

general mixed differential system；eigenvalue；vector eigenfunction；the upper bound

O175.1

A

1008-5475(2016)04-0027-08

10.16219/j.cnki.szxbzk.2016.04.008

2016-06-19；

2016-07-17

苏州市职业大学青年基金资助项目(2010SZDQ12)

卢亦平(1978-)，女，吉林白山人，讲师，硕士，主要从事算子特征值估计研究.

卢亦平，钱椿林.一般混合微分系统第二特征值的上界估计[J].苏州市职业大学学报，2016，27(4)：27-34.