基于Gram行列式的快速端元提取方法
2016-02-07陈金勇
孙 康,帅 通,陈金勇
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079)
基于Gram行列式的快速端元提取方法
孙 康1,2,帅 通1,陈金勇1
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079)
高光谱图像端元提取往往涉及到高维空间中单形体体积的计算,使用无需降维的体积公式能够避免信息损失,但却具有极大的计算复杂度。针对这一缺点进行了研究,提出了基于Gram行列式快速的端元提取算法。该算法不需要计算单形体体积,而是利用了体积公式的递推关系,大大降低了计算复杂度。模拟和真实数据试验表明,该算法在保证高精度端元提取的同时,具有极快的端元提取速度。
高光谱图像;端元提取;单形体;线性混合模型;Gram行列式
0 引言
混合像元分析是高光谱遥感中信息提取的重要手段之一,端元提取(Endmember Extraction)是混合像元分析至关重要的步骤。现有的端元提取方法可以分为端元选择和端元生成2大类[1]。常见的端元选择算法包括N-FINDR[2]、VCA[3]和GEM[4]等。这类算法的主要优点是计算量小,但是需要纯像元假设。与端元生成方法(如MVC-NMF[5]和GOM[6])相比,端元选择往往具有较低的计算复杂度,并且获得的端元具有实际物理意义,因此得到了广泛研究和应用。
端元选择的最重要的依据之一是端元构成的单行体体积最大。基于最大体积的原则,发展了大量的算法如N-FINDR、SGA[7]、OBA[8]和MVHT[9]。然而对于这些基于体积的算法而言,有些需要降维,如N-FINDR、SGA以及MVHT,这会造成一定的信息损失。
耿修瑞等提出了一种不需要降维的体积公式[10],使用该体积公式进行端元选择得到的结果优于需要降维的算法,本文中,该算法称为New Volume Formula for Simplex(NVFS)。由于不需要降维,这个算法能够有效地提取低概率目标的端元,但是一个严重的缺点是计算太慢。本文提出了一种基于Gram行列式的快速端元选择算法——Gram Determinant Based Algorithm(GDA),使得端元提取的计算复杂度大大降低,同时具有更优的端元提取结果。
1 端元提取背景
1.1 线性混合模型原理
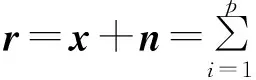
1.2 高维空间单形体体积
对于p个端元,记为ei(i=1,…,p),为了计算端元所构成的体积,一个经常使用的体积公式如下:
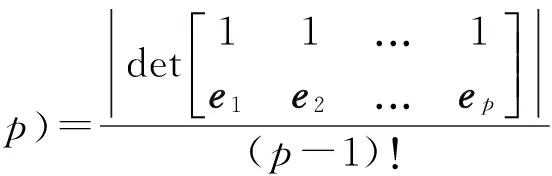
(1)

耿修瑞在文献[10]中给出了一个不需要降维的体积公式:
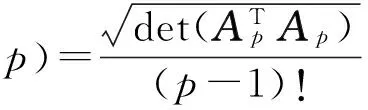
(2)
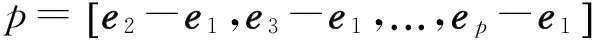
从式(2)可以看出,由于ATpAp始终都是方阵,因此不需要降维也可计算体积。Ap中所有端元都减去e1,表示将数据移至以e1为原点。NVFS使用的就是如式(2)所示的体积公式,在进行端元提取时,NVFS采用了跟N-FINDR相同的策略,先随机初始化端元,然后逐像元计算体积,取得最大体积的像元作为新入选端元,直至体积不再增大。NVFS对于每个像元都要反复计算其与其他端元构成的体积,加上该体积表达无需降维,因此计算量极大,限制了其在实际中的应用。同时受随机初始化的影响,计算结果并不稳定[11]。
2 基于Gram行列式的端元提取
2.1 端元初始化策略改进
在进行端元提取之前,需要确定端元的个数,本文中使用虚拟维数VD[12]估计。NVFS先随机产生所有端元,然后再逐个替换,直至不能替换为止,一般要运行3~5次才收敛[13]。由于式(2)计算体积与维数无关,因此可以采取类似SGA的策略,一个一个地按顺次求取端元,这样程序只需要运行一次即可,而且结果具有可重复性。
在进行端元初始化的时候,第1个端元的选取是基于这样的事实:距离原点最远的像元必是端元[4],因此本文选择亮度最大的像元作为第1个端元。然后再按照式(2)计算体积,体积最大的就是第2个端元,依次进行下去,直至所有的端元全部提取为止,这样只进行一次外部循环即可,同时结果具有鲁棒性。
2.2 端元得分指标设计
在使用式(2)作为体积公式提取第k个端元时,令Bk=ATkAk,当k≥2时,可以发现Bk和Bk+1之间有如下递推的关系:
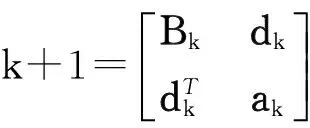
(3)
式中,
dk=[(ek+1-e1)T(e2-e1),(ek+1-e1)T(e3-e1),…, (ek+1-e1)T(ek-e1)]T;
ak=(ek+1-e1)T(ek+1-e1)。
依据分块矩阵行列式计算规则[14]矩阵,可以推导出Bk和Bk+1的行列式之间的关系为:
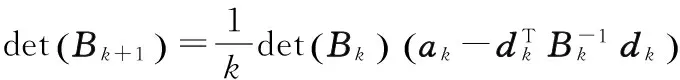
(4)
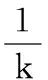
2.3 方法计算复杂度分析
令p为端元数,N为像元数,L为波段数,则NVFS需要对所有像元依次计算体积det(Bp),而计算p阶方阵的行列式计算复杂度为pη,2.3≤η≤2.9[14],计算Bp需要(p-1)L次乘法(L为波段数),因此替换一个端元所需的计算量为(pη+pL-L)N(N为像元数目)。该算法需要替换p个端元,且一般需要替换3~5次才会收敛,因此提取p个端元,NVFS中所需的计算复杂度为σ(pη+1+p2L-pL)N,其中2.3≤η≤2.9,3≤σ≤5。
在同样大小数据下,对于GDA,每次循环只需计算每个像素的端元得分ak-dTkB-1kdk,在一次循环中,所有像元“共享”ak和B-1k,因此只需计算一次,然后计算各个像元的端元得分指标,端元得分指标最大的像元就是新的端元。dk的计算需要L次乘法,N个像元的第k+1个端元得分指标ak-dTkB-1kdk需要的乘法次数为(k2+L)N。因此使用GDA提取p个端元,需要p-1次循环,而初始化第一个端元的计算量为L*N,故GDA所需的总计算量为:
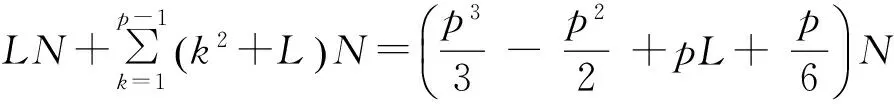
可以看出,GDA使得计算量大大减少。值得一提的是端元得分指标的表达形式为二次型,对其规范化以后,可以使用快速的矩阵乘积代替逐像元的循环计算。
3 方法性能分析与验证
本文将对N-FINDR、SGA、MVHT、NVFS、OBA和本文提出的算法这6种算法进行比较。试验分为模拟数据和实际数据2部分进行,分别比较这6种算法在不同信噪比下提取端元的准确度以及相应的计算时间,其中端元提取的准确度采用rmsSAE和rmsSID[3]作为度量指标。所有试验均在同一配置的机器上进行,硬件配置为CPU Intel (R) Core(TM) i5-2400@3.10 GHz,内存2 GB,系统环境Windows XP Professional Service Pack 3,使用Matlab 7.0作为软件编译环境。
3.1 模拟数据试验
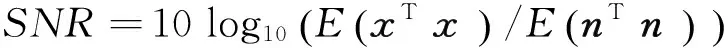
3.1.1 试验1:端元精确度比较
使用上述方法产生了10 000个像元,并且加入一系列强度的高斯白噪声,SNR分别为10 dB、15 dB、20 dB、25 dB和30 dB。各个方法提取端元的rmsSAE和rmsSID结果如表1所示。
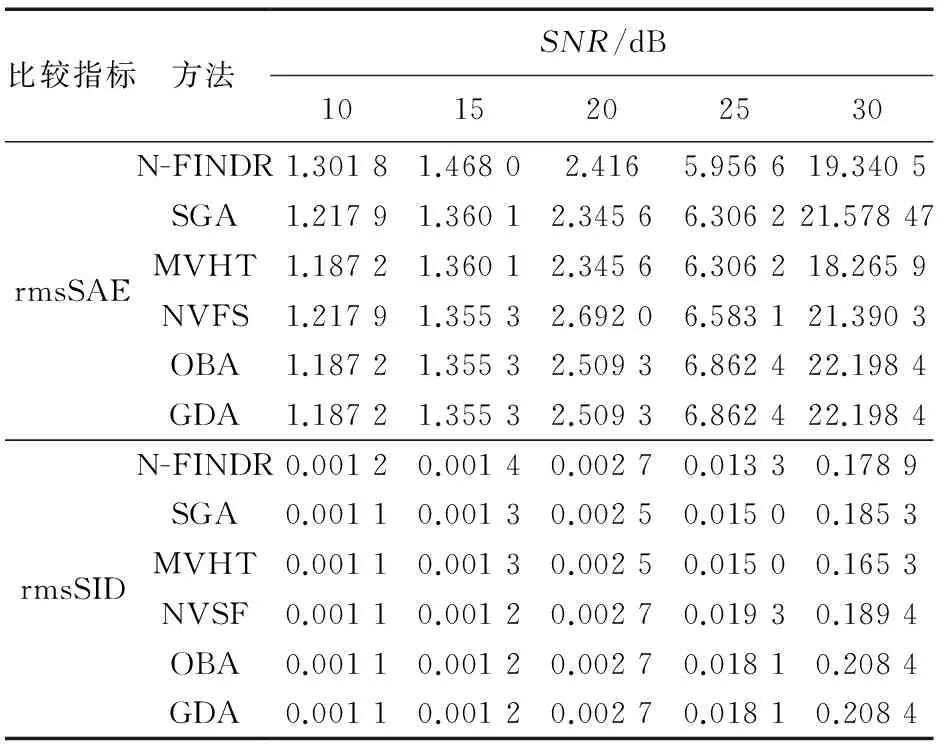
表1 不同方法的端元选择结果精度比较
从表1中可以看出,GDA与OBA的端元提取结果是一样的,这是因为二者使用的体积公式是相同的,而且选择初始端元的方法是一样的。
表1的对比结果表明,所有算法的性能都随着SNR的降低而降低(N-FINDR有几次例外情况,但多次平均之后也符合这个规律)。在SNR较高时(SNR为30 dB和25 dB时),使用式(2)的算法,端元提取性能较好,这是因为算法不需要降维,能够全面地利用所有光谱信息,因而可以获得更为准确的结果。而需要降维的算法,降维之后信息会有所损失。值得注意的是,本文改进了NVFS的初始化方式及搜寻策略之后,算法性能也有所提高。
3.1.2 试验2:端元得分指标随端元数的变化
此外,本文还发现端元指标的一个重要特性,即端元指标随着端元数目的增加单调下降。本试验分别用4、5、6、7和8个实际端元产生模拟数据,并控制噪比为30 dB,然后分别比较了估计端元数从1~15时,端元得分随端元数的变化趋势,结果如图1所示。
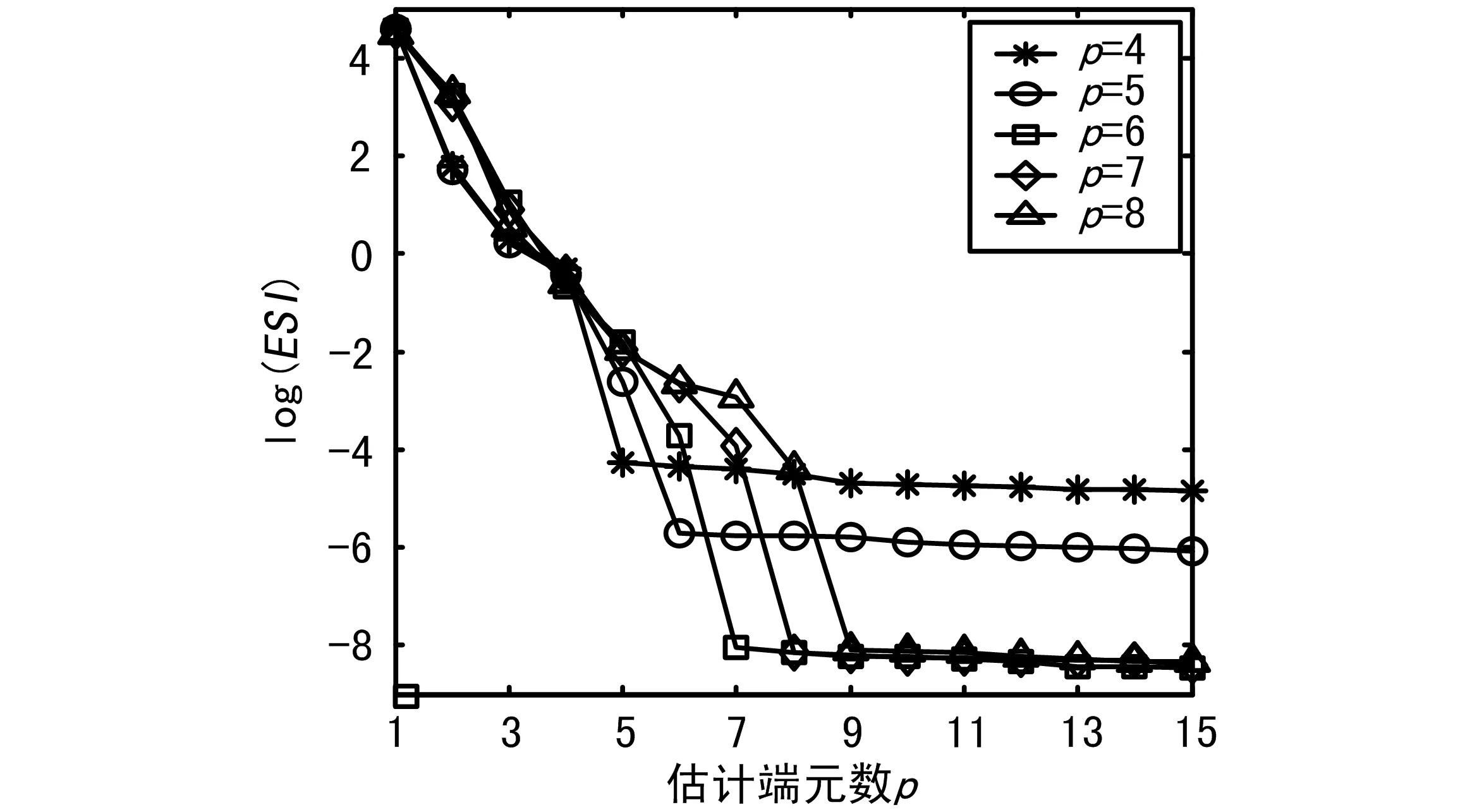
图1 端元得分随端元数的增加而单调下降
从图1中可以看出,端元得分随着估计端元个数的增加是单调下降的。当估计端元数目小于实际端元数目时,下降的速度很快;当估计端元数目等于实际端元数目时,该得分急速下降,对于绝大多数情况,此时下降幅度最大;而当估计端元数目大于实际端元数目的时候,该得分几乎不变。因此,端元得分可以看作是端元的重要程度,本算法中,最重要的端元最先被找出来,之后提取的端元重要程度是依次下降的。当提取到某个端元重要程度急速下降时,则意味着提取的端元已经比实际端元多了一个,如果此后端元得分指标变化异常平缓,则更加说明已经提取了足够的端元。端元得分的这个性质可以为估计端元数目提供一种辅助性的手段。
3.1.3 试验3:程序运行时间比较
本文还比较了在固定端元个数的情况下,计算时间随像元个数的变化情况,考虑到实际端元情况,试验选取p=6,结果如图2所示。
从图2可以看出,在端元个数固定为6个时,所有算法的计算时间随像元数都成相同的变化趋势,这是因为这些算法的时间对于像元个数N是同样的一次函数。GDA是计算速度最快的算法,它在提取600*600大小的图像中的6个端元用时仅为0.25 s。
3.2 真实高光谱数据试验
这部分试验中,本文使用实际高光谱数据检验上述几种算法的性能。数据是由AVIRIS获取的Nevada Cuprite矿区图像。图像大小为190*250,包含从370~2 500 nm的224个波段,光谱分辨率大约10 nm,去除了水汽严重吸收以及信噪比较低的1~2、104~113、148~167以及221~224的36个波段,剩余188个波段。在使用VD[12]进行维数估计发现,端元数目随着不同的虚警率在16~20之间。参照其他的试验,本试验令端元数目p=18。
各个方法的计算时间以及获得的体积如表2所示。从表2中可以看出,GDA能够获得最大的端元体积,由于各个算法的目标函数是获得最大体积,因此GDA的性能是最优的。此外,GDA的计算时间仅为0.607 3 s,具有最高的计算效率。

表2 不同算法的计算时间以及获得的体积
为进一步对各个端元精度进行比较,本文将各方法提取的典型端元与USGS光谱中对应的光谱进行比较,比较的指标为光谱角度,结果如表3所示,其中“-”表示没有提取到相应端元。
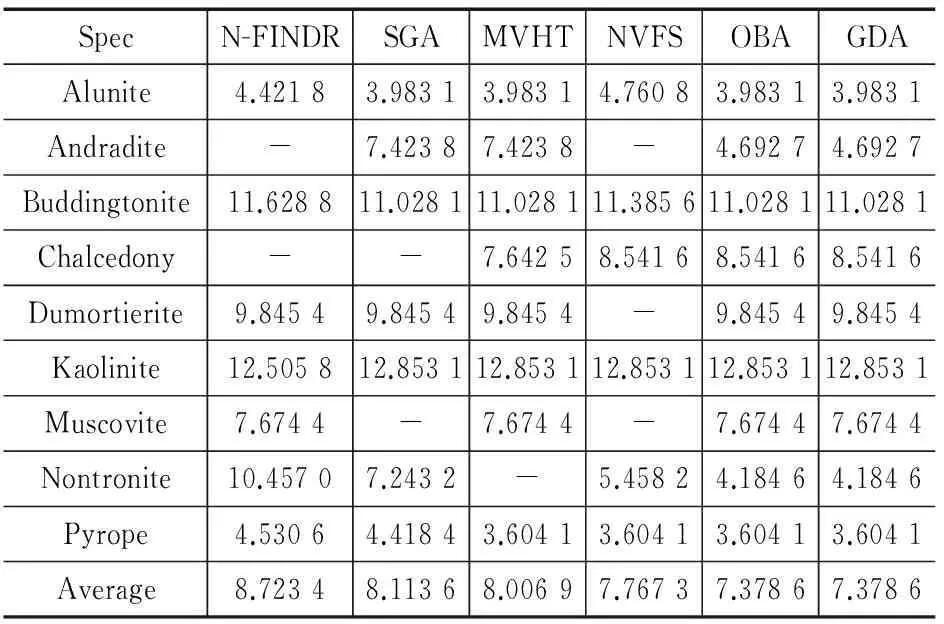
表3 不同算法提取的端元与USGS光谱库中光谱的角度(°)
表3中的数据表明,使用式(2)的端元提取方法(NVFS、OBA和GDA)获得的端元提取精度高于使用式(1)的算法(NFINDR、SGA和MVHT)。与NVFS相比,GDA使用顺次提取端元的方式提高了端元提取精度。尽管GDA在提取某些端元时,如(Kaolinite等),精度比一些算法低了一些,但是GDA提取的端元的精度整体优于其他算法。
4 结束语
端元提取使用无需降维的体积公式可以避免信息损失,因而能更准确地选择所需的端元,然而该算法具有极高的计算复杂度。本文提出了一种快速端元选择算法GDA,在保证提取端元精度的同时,使速度有了极大的提升。相对于其他基于体积的端元选择算法,GDA具有不需要降维、计算量小、可以提供一个端元数据参考指标以及较高鲁棒性等优点。
[1] BIOUCAS-DIAS J M,PLAZA A,DOBIGEON N,et al.Hyperspectral Unmixing Overview:Geometrical,Statistical,and Sparse Regression-based Approaches[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(2):354-379.
[2] WINTER M E.N-FINDR:an Algorithm for Fast Autonomous Spectral End-member Determination in Hyperspectral Data[C]∥SPIE’s International Symposium on Optical Science,Engineering,and Instrumentation,1999:266-275.
[3] NASCIMENTO J M,BIOUCAS-DIAS J M.Vertex Component Analysis:a Fast Algorithm to Unmix Hyperspectral Data[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(4):898-910.
[4] GENG X,XIAO Z,JI L,et al.A Gaussian Elimination Based Fast Endmember Extraction Algorithm for Hyperspectral Imagery[J].ISPRS Journal of Photogrammetry and Remote Sensing,2013(79):211-218.
[5] MIAO L,QI H.Endmember Extraction from Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(3):765-777.
[6] GENG X,JI L,ZHAO Y,et al.A New Endmember Generation Algorithm Based on a Geometric Optimization Model for Hyperspectral Images[J].IEEE Geoscience and Remote Sensing Letters,2013,10(4):811-815.
[7] CHANG C I,WU C C,LIU W M,et al.A New Growing Method for Simplex-based Endmember Extraction Algorithm[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(10):2 804-2 819.
[8] TAO X,WANG B,ZHANG L,et al.A New Endmember Extraction Algorithm Based on Orthogonal Bases of Subspace Formed By Endmembers [C]∥Geoscience and Remote Sensing Symposium,2007:2 006-2 009.
[9] LIU J,ZHANG J.A New Maximum Simplex Volume Method Based on Householder Transformation for Endmember Extraction[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(1):104-118.
[10]GENG X,ZHAO Y,WANG F,et al.A New Volume Formula for a Simplex and Its Application to Endmember Extraction for Hyperspectral Image Analysis[J].International Journal of Remote Sensing,2010,31(4):1 027-1 035.
[11]PLAZA A,CHANG C I.Impact of Initialization on Design of Endmember Extraction Algorithms[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(11):3 397-3 407.
[12]CHANG C I,DU Q.Estimation of Number of Spectrally Distinct Signal Sources in Hyperspectral Imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(3):608-619.
[13]PLAZA A,MARTINEZ P,PEREZ R,et al.A Quantitative and Comparative Analysis of Endmember Extraction Algorithms from Hyperspectral Data[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(3):650-663.
[14]BAUR W,STRASSEN V.The Complexity of Partial Derivatives[J].Theoretical Computer Science,1983(22):317-330.
孙 康 男,(1988—),博士,工程师。主要研究方向:遥感图像处理与高性能计算的研究。
陈金勇 男,(1970—),研究员。主要研究方向:航天信息处理与航天地面应用系统研究。
A New Endmember Extraction Method Based on Gram Determinant
SUN Kang1,2,SHUAI Tong1,CHEN Jin-yong1
(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China;2.StateKeyLaboratoryofInformationEngineeringinSurveying,MappingandRemoteSensing,WuhanUniversity,WuhanHubei430079,China)
The endmember extraction methods for hyperspectral imagery generally involve the computation of simplex volume in high-dimension space.The employment of volume without dimensionality reduction though avoids the information loss,suffers from high computational complexity.This paper puts forward a new endmember extraction method based on Gram determinant which is expected to relieve the efficiency issue.The algorithm does not involve the computation of the volumes,instead,it uses the recurrence relationship of volumes which greatly reduces the computational complexity.The experiments on simulated and real datasets verify the accuracy and efficiency of the proposed method.
hyperspectral imagery;endmember extraction;simplex;LMM;Gram determinant
10.3969/j.issn.1003-3106.2016.11.07
孙 康,帅 通,陈金勇.基于Gram行列式的快速端元提取方法[J].无线电工程,2016,46(11):26-29,46.
2016-08-22
中国博士后科学基金资助项目(2015M580217);河北省博士后科学基金资助项目(B2015005003)。
TP751
A
1003-3106(2016)11-0026-04
