不确定性供应链中基于模糊线性规划的订单分配方案*

王 娟， 尹小悦， 陈昭玖

(1.赣南医学院 人文社科学院，江西 赣州 341000;2.江西农业大学 经济管理学院，江西 南昌 330045)



不确定性供应链中基于模糊线性规划的订单分配方案*

王 娟1*， 尹小悦1， 陈昭玖2

(1.赣南医学院 人文社科学院，江西 赣州 341000;2.江西农业大学 经济管理学院，江西 南昌 330045)

现实供应链中供应商具有多项不确定性，加大了订单合理分配的难度，为此提出一种基于模糊线性规划的订单分配方案.首先，运用模糊集理论来表示供应商指标中的不确定性.然后，根据供应商的输出指标，运用数据包络分析法对其进行效率评估并排序.最后，在综合考虑供应商交易效率、交货时间和采购成本下，利用提出的模糊线性规划模型求解订单分配方案.案例分析中，以各项指标的加权和评估了所得分配方案的性能.结果表明，该方法能够获得合理的分配方案且对不确定性具有鲁棒性.

订单分配；不确定性；模糊集理论；数据包络分析；线性规划

企业供应链(Supply Chain, SC)[1]是指从采购到满足最终客户需求的所有过程，供应链的有效管理能够使其高效地运作，以较少的成本把优良产品及时交付给客户.供应链管理包括订单分配、加工制造、采购、库存管理等操作.其中，订单分配是指将规定时间内所需的订单任务分配给各个供应商.由于各供应商在生产成本、生产能力、产品质量和交付时间等方面都存在较大差异，所以如何对订单进行合理分配，以获得更好的价格、质量和服务水平，是订单分配中的关键问题[2].

目前，学者提出了多种订单分配的优化方案，主要技术有层次分析法、线性规划、数据包络分析、神经网络等.例如，[3]基于一种混合整数线性规划模型来选择最佳供应商并确定最佳订单分配数量，以此最大限度地降低采购成本.[4]基于层次分析法进行订单优化分配，综合考虑了成本和供货可靠性.[5]引入了数据包络分析法来评估供应商效率，并对供应商进行排名，然后采用线性规划方法获得每个供应商的最佳订单数量.这些方法都能够很好地实现所设定的目标.然而却存在一个重要的缺陷，即在求解订单分配过程中，所采用的供应商指标数据都是固定的.在现实生产过程中，存在很多的不确定性，导致供应商的生产成本、供货周期和产品质量等会发生变化[6].所以，在订单分配中需要考虑到这些不确定性.

基于上述分析，提出了一种不确定性条件下的供应链订单分配方案.该方案采用一种模糊数据包络分析(Data Envelopment Analysis, DEA)方法，以模糊数来表示参数的不确定性，以此评估各供应商的交易效率.然后，构建一个模糊线性规划(Fuzzy Linear Programming, FLP)模型，以供应商的交易效率、交货时间和采购成本的模糊表示为输入，在考虑供应商供货能力下，求解订单分配方案.最终获得一个具有较大效率、较小成本和交货时间的分配方案.

1 提出的订单分配方法

提出的订单分配方法主要分为2个步骤：基于模糊DEA来评估供应商交易效率并排名；基于供应商交易效率、交货时间和采购成本，利用一种FLP模型来求解订单分配方案.

1.1 供应商效率评估

将模糊集理论(Fuzzy Set Theory, FST)[7]与DEA相结合，形成模糊DEA方法，增强了对供应商的辨别能力，以此对供应商进行效率评估和排名.DEA不需要数据规范化、具有较高的供应商辨别能力和在多采购背景下的适用性等优势[8]；而模糊方法具有处理不确定性数据的能力.这里，供应商的交易效率为该供应商在各种输出指标下的综合评价.

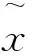
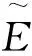
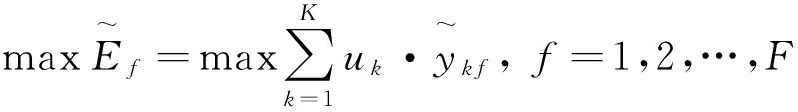
(1)

约束于：

(2)

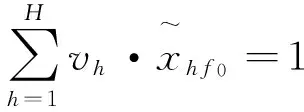
(3)

uk,vh≥0 , k=1,2,…,K;h=1,2,…,H，

(4)

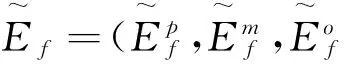
1.2 订单分配

上一步对供应商的效率进行了评估和排名.然而，在实际运营过程中，最有效地供应商也可能不能在交付时间内满足所有需求.这会影响服务质量和可靠性，如果与客户建立合同协议，甚至可能会受到相应延误损失.因此，不能简单地仅依靠供应商效率来分配订单.为此，本文折中考虑了供应商效率、货物成本和交货时间，同时尊重每个供应商的供货能力约束，在不确定环境下求解订单分配方案.

构建一种模糊线性规划(FLP)模型[9]，在给定供货能力情况下，权衡考虑交易效率、交货时间和采购成本，最终输出每个供应商的订单量.该问题的FLP模型表示为：

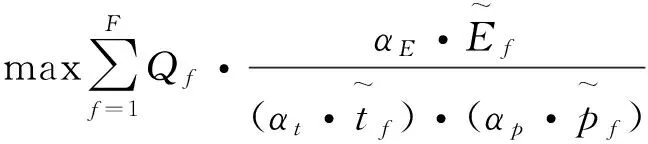
(5)

约束于：

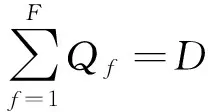
(6)

0≤Qf≤ACf∀f=1,…,F，

(7)

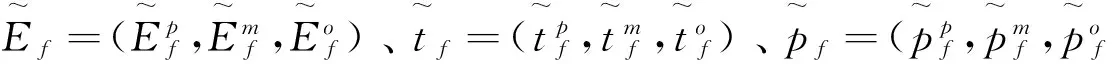
2 订单分配方案的性能评估

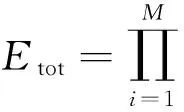
(8)

3 案例分析

3.1 订单分配案例

本文采用[10]中的订单分配案例，其中具有8个供应商.采用MATLAB软件构建最优化问题模型；利用GLPK优化工具求解线性规划模型；PC配置为Intel酷睿i5内核、3.4 GHz处理器、8 GB RAM.

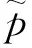
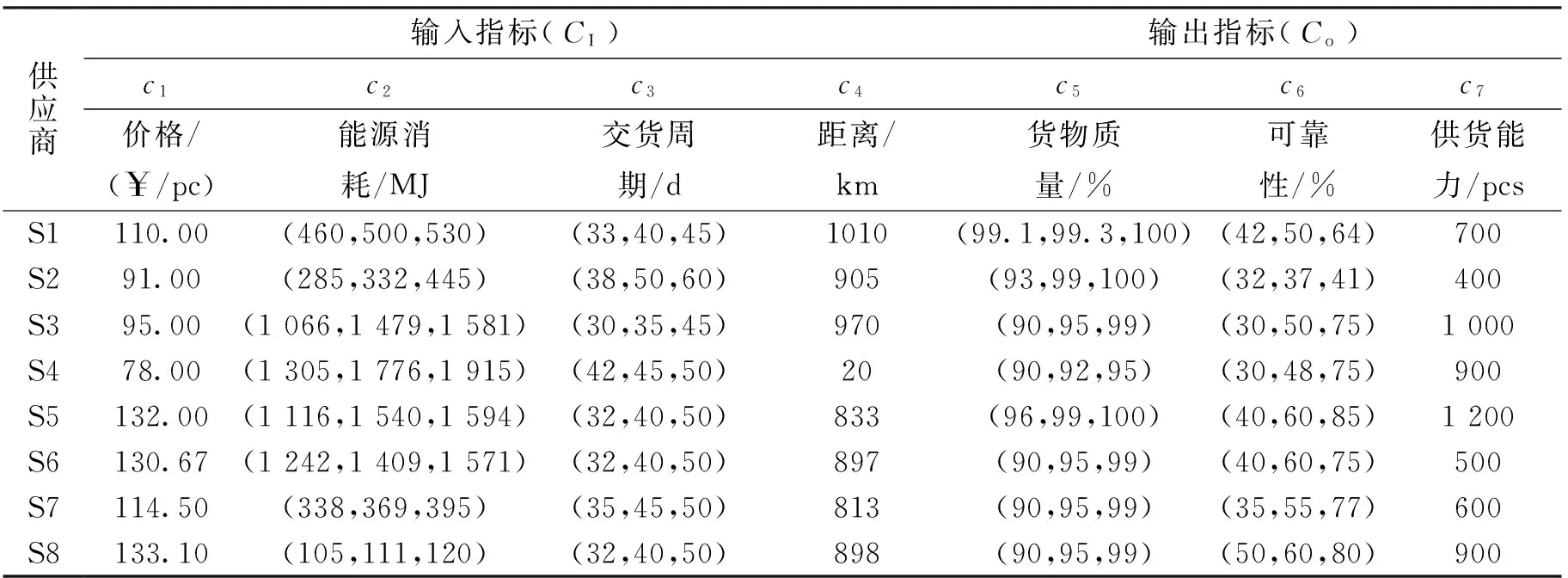
表1 候选供应商的各项指标参数Tab.1 All index parameter of candidate suppliers

另外，采购商可以根据生产需要，制定一些约束保障，为不同指标分配不同的重要性权重.例如，可设定价格是最重要的考虑指标，其次是交货时间等.在本文实验中，为了简单起见，设定所有指标的权重都相等.

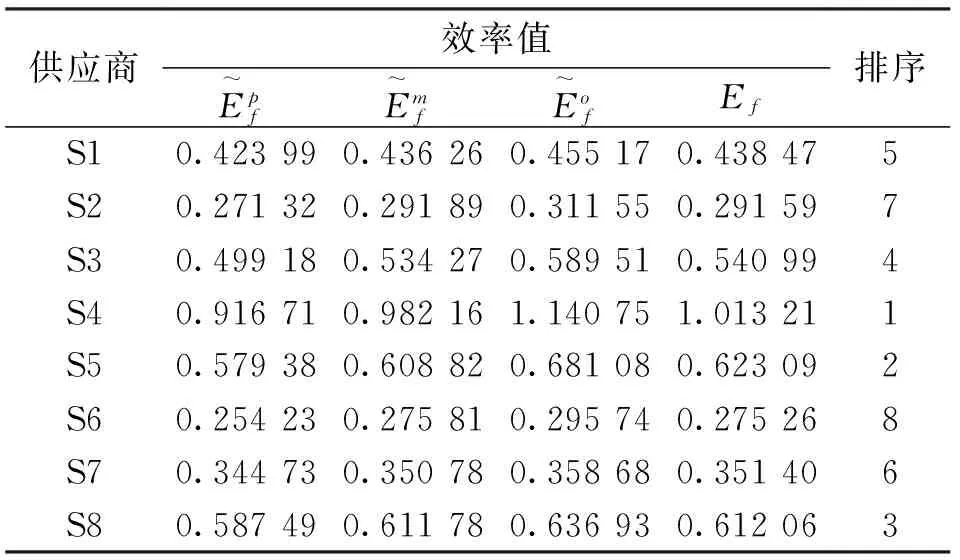
表2 各供应商的模糊效率Tab.2 The fuzzy efficiency of suppliers

表3 获得的订单分配方案Tab.3 The order allocation scheme

3.2 求解订单分配方案

首先，执行步骤1：供应商效率评估.利用模糊DEA方法来对各候选供应商的效率进行评估并排序，结果如表2所示，其中最优的供应商为S4，其次是S5.

接着，执行步骤2：订单分配.将上一步骤中获得的模糊效率值、交货时间和成本作为步骤2的输入.设这些指标的重要性相同，即αE=αt=αc=1.另外，设定总订单量为D=2 500件.然后求解模糊线性规划模型，获得分配方案，各供应商所分配的供货量如表3所示.其中，选择了S1 、S4 、S5和 S7这4个供应商来供货，分别分配的订单量为541、701、658和600个.

3.3 订单分配方案的性能评估

在获得订单分配方案后，基于效率、成本和交货时间来评估分配方案的性能.其中，设置输入参数：所要求的交货时间(T=40 d)和每日延误惩罚(cpen=200￥/d).

将步骤2获得的订单分配方案与其他3种分配方案进行比较：方案1(最有效)，仅根据供应商的效率指标对其进行排名，并按照递减序列选择供应商进行分配订单，直到满足总订单需求量为止；方案2(最低廉)，仅根据价格指标升序选择供应商；方案3(最快速)，仅根据交货时间指标升序选择供应商.4种分配方案的整体交易效率Etot、整体采购成本ctot、整体交货时间ttot和延误损失pentot评估结果如表4所示.

对于每种指标，计算各方案与理想解决方案的偏差比，然后根据式(8)计算各偏差比的加权平均值，其中设各权重系数都等于1，结果如表5所示.

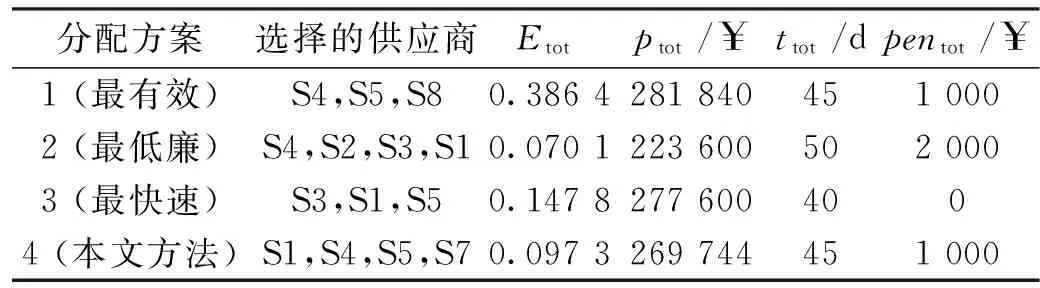
表4 4种订单分配方案的评估结果Tab.4 Evaluation results of four order allocation scheme

表5 各分配方案与理想方案的比较Tab.5 The comparison of each scheme and ideal scheme

可以看出，方案1在效率方面，方案2在成本方面，方案3在时间和损失方面与理想方案相同，但其他方面与理想方案相差很大，不能做到很好的均衡.而本文获得的分配方案在各个方面与理想方案都比较接近，且最终性能偏差比例的加权平均只比理想方案低了约9.65%，证明了该方案是一种在效率、成本和交付时间方面都比较折中的方案.

值得注意的是，该实验获得订单分配方案中，各评判指标的权重都设定为相等.当然，采购商可以根据自己的需求设定不同的权重.

4 结束语

由于实际生产管理中存在很多不确定性因素，影响着供应链管理效率.为此，提出了一种用于存在不确定因素下的供应链管理中的订单分配优化方法.通过模糊集理论表示供应商的不确定性，利用数据包络分析法来评估供应商的交易效率.在综合考虑交易效率、交货时间和成本下制定最优分配方案.实验结果表明，提出的方案能够根据用户需求获得多指标均衡的分配方案，非常适合于中小型企业的订单分配.

[1] 史玉雷, 陆志强. 基于供应商经济生产批量的供应链订单分配问题[J]. 上海交通大学学报, 2011, 45(12):1747-1752.

[2] 项薇, 宋法帅, 叶飞帆. 基于生产负荷率均衡的多供应商订单分配仿真[J]. 系统仿真学报, 2013, 25(2): 209-215.

[3] NAZARI-SHIRKOUHI S, SHAKOURI H, JAVADI B, et al. Supplier selection and order allocation problem using a two-phase fuzzy multi-objective linear programming[J]. Applied Mathematical Modelling, 2013, 37(22): 9308-9323.

[4] ERDEM A S, GÖÇEN E. Development of a decision support system for supplier evaluation and order allocation[J]. Expert Systems with Applications, 2012, 39(5):4927-4937.

[5] DOTOLI M,FALAGARIO M. A hierarchical model for optimal supplier selection in multiple sourcing contexts[J]. International Journal of Production Research, 2012, 50(11):2953-2967.

[6] 黄河, 何青, 徐鸿雁. 考虑供应风险和生产成本不确定性的供应链动态决策研究[J]. 中国管理科学, 2015, 23(11): 56-61.

[7] 成央金, 白玉龙, 谢婉莹. 基于粒子群算法的直觉模糊多目标规划[J]. 湘潭大学自然科学学报, 2015, 37(4): 1-5.

[8] 张树梁, 陈友玲, 张豆. 供应链中供应商选择决策方法[J]. 计算机应用研究, 2015, 32(4):1024-1027.

[9] PAKSOY T, PEHIVAN N Y. A fuzzy linear programming model for the optimization of multi-stage supply chain networks with triangular and trapezoidal membership functions[J]. Journal of the Franklin Institute, 2012, 34(1): 93-109.

[10] HATAMI-MARBINI A, EMROUZNEJAD A, TAVANA M. A taxonomy and review of the fuzzy data envelopment analysis literature: Two decades in the making[J]. European Journal of Operational Research, 2011, 21(4): 457-472.

责任编辑：龙顺潮

Order Allocation Scheme in Supply Chain with Uncertainty Based on Fuzzy Linear Programming

WANGJuan1*,YINXiao-yue1,CHENZhao-jiu2

(1.School of Humanities & Social Sciences, Gannan Medical University, Ganzhou 341000；2.School of Economics and Management, Jiangxi Agriculture University, Nanchang 330045 China)

The supplier has many uncertainty factors in real supply chain, which increase the difficulty of the reasonable allocation of orders, so a fuzzy linear programming based order allocation scheme is proposed. First, the fuzzy set theory is used to represent the uncertainty in the supplier's index. Then, the data envelopment analysis is used to evaluate the efficiency of suppliers and sort according to the output index. Finally, the proposed fuzzy linear programming model is used to solve the order allocation problem, which with the comprehensive consideration of the supplier's transaction efficiency, delivery time and purchasing cost. In case analysis, the performance of the allocation scheme is evaluated by weighted sum of the indicators. The results show that the proposed method can obtain a reasonable allocation scheme and is robust to uncertainty.

order allocation; uncertainty; fuzzy set theory; data envelopment analysis; linear programming

2016-04-09

赣州市社联课题(No.14471)

王娟(1985-)，女，江西 赣州人，讲师.E-mail：wangjuangnmu@126.com

O221；F273

A

1000-5900(2016)03-0108-05