各边长均为定值的四边形面积何时最大

曲阜师范大学附属中学

周祎明 (邮编：273165)

山东省济宁市育才中学分校

庄志宏 (邮编：232100)



初数研究

各边长均为定值的四边形面积何时最大

曲阜师范大学附属中学

周祎明 (邮编：273165)

山东省济宁市育才中学分校

庄志宏 (邮编：232100)

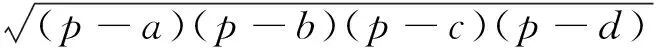
证明 若四边形ABCD是凹四边形，可不妨设点A在△BCD内(如图1所示).

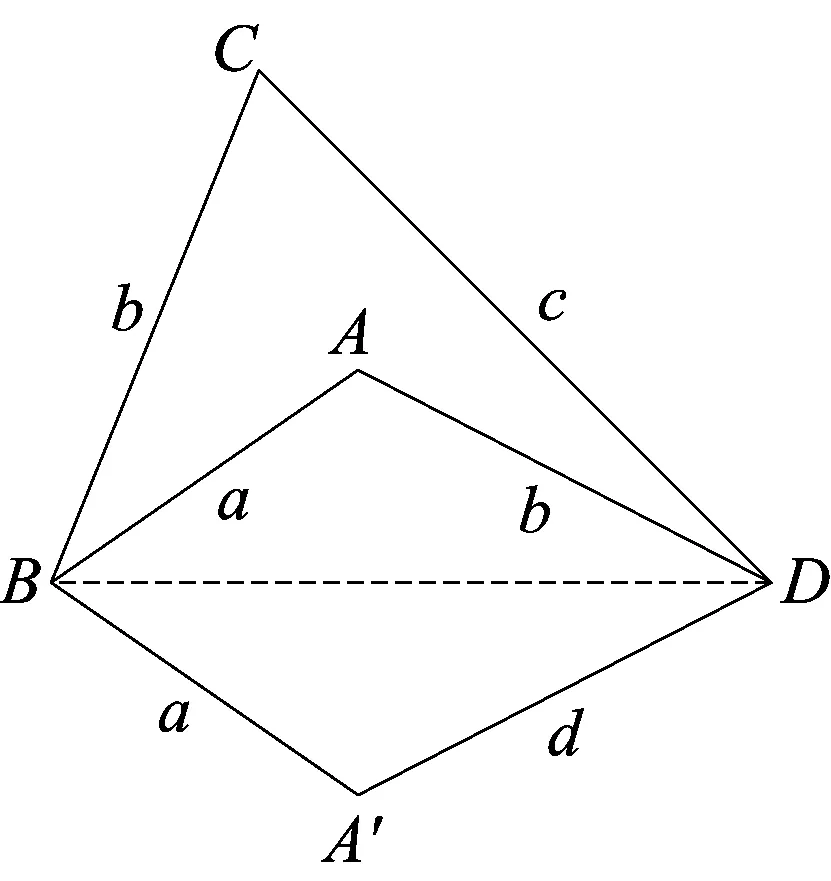
图1

连结BD，作点A关于直线BD的对称点A′.可得四边形A′BCD的各边长分别为A′B=a,BC=b,CD=c,DA′=d,但凸四边形A′BCD的面积大于凹四边形ABCD的面积，所以当四边形ABCD的面积最大时，该四边形是凸四边形.

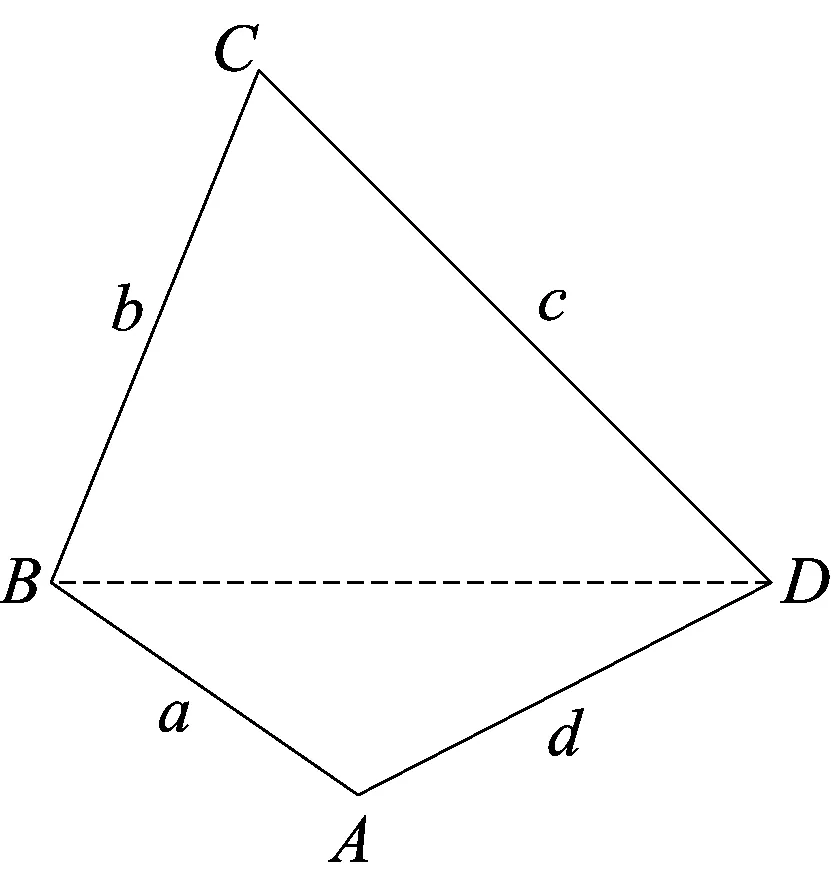
图2

如图2所示，在凸四边形ABCD中，连结BD.

在△ABD和△CBD中，由余弦定理，可得

BD2=b2+c2-2bccosC=a2+d2-2adcosA,

(a2+d2)-(b2+c2)=2adcosA-2bccosC.

①

还可得，凸四边形ABCD的面积

②

由①2+②2，可得

[(a2+d2)-(b2+c2)]2+16S2=4a2d2+4b2c2-8abcdcos(A+C)，

16S2≤(4a2d2+4b2c2+8abcd)-[(a2+d2)-(b2+c2)]2(当且仅当A+C=π时取等号)

=(2ad+2bc)2-[(a2+d2)-(b2+c2)]2=(2ad+2bc+a2+d2-b2-c2)(2ad+2bc-a2-d2+b2+c2)=[(a+d)2-(b-c)2][(b+c)2-(a-d)2]=(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)=(2p-2c)(2p-2b)(2p-2d)(2p-2a).

所以S2≤(p-a)(p-b)(p-c)(p-d),

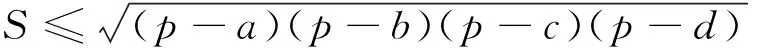
推论 (1)各边长分别是a、b、c、d的圆内接四边形的面积为

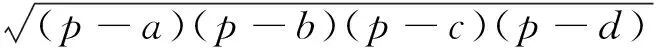
(3)在周长为定值的四边形中，当且仅当其是正方形时该四边形的面积最大．

证明 (1)由定理立得.

(2)在结论(1)中让d→0即得.

(3)设周长为定值的四边形的各边长分别是a,b,c,d(a+b+c+d=定值2p)，由定理得该四边形的面积

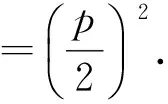
进而可得结论成立.

2016-08-28)