车刀刀尖圆弧半径对车削质量的影响分析

王守志，韩金玉

(天津中德应用技术大学 航空航天与汽车学院，天津 300350)

车刀刀尖圆弧半径对车削质量的影响分析

王守志，韩金玉

(天津中德应用技术大学 航空航天与汽车学院，天津 300350)

根据数控车刀与被加工表面的几何关系，提出了X向、Z向和法向加工误差模型和算法，分析了各方向加工误差的影响因素，探讨了加工误差与切线倾角、刀尖圆弧半径的关系，并剖析了各方向误差对车削质量的影响。分析表明由于车刀刀尖圆弧的存在，会产生X向、Z向和法向加工误差，各方向误差随刀尖半径的增大而增大，X向和Z向误差与切线倾角呈单调非线性关系，切向误差呈下开口曲线关系；且各方向误差对被加工工件的形状精度和尺寸精度均有影响，对于不同的工件形状其影响不同。

车刀；圆弧半径；车削质量；影响

0 前言

车刀刀尖的实际几何形状是一段折线或圆弧以及其他可能的曲线[1]，理想的刀尖并不存在[2-3]。在数控车削加工中，为补偿刀尖半径误差，提高加工精度，多数数控系统常将对刀位置作为假想刀尖点进行编程与加工[4]。在加工圆锥面、圆弧面等与Z轴或X轴不平行的表面时，理想刀位点与实际切削点的不一致，使实际加工表面偏离于编程表面，产生加工误差。这种误差对精密加工影响较大。为此，许多学者探讨了刀尖圆弧半径对车削质量的影响规律，如周建来等人提出一种基于试切法的刀尖圆弧半径补偿模型[1]，吴志清、杨锦涛、徐丽霞等人分析了刀尖圆弧半径对锥面和圆弧面的加工质量影响，论述了误差消除的途径[3-5]，李英平、高晓东、殷小清等人定性地分析了刀尖圆弧半径对车削质量的影响[6-8]。但是，这些文献多是定性分析或近似分析，且部分文献只是分析了刀尖半径对圆锥面和圆弧面的加工影响。因此，本文在分析实际切削点与被加工表面之间的位置关系基础上，建立刀尖圆弧半径引入的加工误差模型，定量分析刀尖半径以及切线倾角对加工误差的影响，探讨了刀尖圆弧半径对零件车削质量的影响规律，以指导刀尖圆弧半径误差补偿，提高加工精度、保证加工质量。

1 刀尖半径误差模型

数控车削程序是以试切法等对刀方法确定的车刀刀尖固定位置P为假想刀尖点，按照工件轮廓尺寸编制的[7]。而实际上，车刀刀尖轮是一条很难确定的曲线。当加工圆锥面、圆弧面或曲面时，实际切削点与假想刀尖点不重合，引起加工误差。这种由于刀尖半径的存在而引入的加工误差，本文简称刀尖半径误差。为补偿刀尖半径误差，多数数控系统将刀尖轮廓曲线简化为理想圆弧，其圆弧半径即为刀尖圆弧半径R，简称刀尖半径，其取值一般为0.2mm～1.6mm[9]。为简化分析，本节以理想圆弧为刀尖轮廓曲线分析因刀尖半径而引入的加工误差，如图1、图2所示。

图1 车刀刀尖

图2 试切法对刀

由切削原理知，不管切削何种锥面或曲面，在实际切削点Q处刀尖圆弧的切线与被切削面的切线CD重合。定义实际切削点Q处，被切削表面的切线CD斜角α为切线倾角。切削圆锥面时，假想刀尖点与切点Q、车刀圆弧圆心O的几何关系如图3所示。此时，数控系统真正诉求的切削点是P点，与实际切削点为Q点不一致，不论在X向和Z向，还是实际切削点Q的法向都产生了加工误差。

图3 切削圆锥面

由几何关系可知，MN∥CD,OK⊥CD，且∠KPQ=∠BOQ=α，则在切削点Q处的各方向加工误差分别为：

e=OK-OQ=OP×cos(β-α)-R

(1)

eX=PA-OT=PA-Rcosα

(2)

eZ=PB-QT=PB-Rsinα

(3)

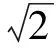
(4)

eX=R×(1-cosα)

(5)

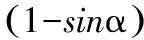
(6)

切削圆弧面、圆角等曲面时，假想刀尖点与切点Q、刀尖圆弧圆心O的几何关系如图4所示。同理可推导出与式(4)、(5)、(6)相同的加工误差数学模型。

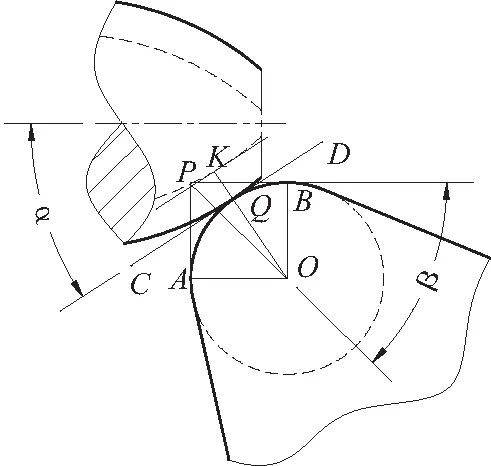
图4 切削曲面

但需要注意的是车削锥面时，切线倾角为固定值，是圆锥锥角的一半，而车削曲面时，其切线倾角是随着加工位置的变化而变化的，不是固定不变的。

2 刀尖半径误差的影响因素分析

由式(4)、式(5)和式(6)可知，各方向加工误差与刀具圆弧半径R及实际切削点处的切线倾角α均有关系。为探索各方向加工误差与影响因素之间的变化规律，本节分别分析刀尖半径及切线倾斜角对加工误差的影响。

2.1 切线倾角对加工误差的影响

由式(4)可知，当切线倾角α在0°与45°之间变化时，切向加工误差e随切线倾角α的增大而增大；α在45°与90°之间变化时，切向加工误差e随切线倾角α的增大而减小。而且，切线倾角α=0°或α=90°时，其法向加工误差为零，即切削与X轴或Z轴平行的平面或圆柱面时，不存在法向加工误差。车刀圆弧半径R分别为0.4mm和0.6mm时，切向加工误差e与切线倾角α的关系如图5所示。关系图也反映了加工误差与对切线倾角之间的这种下开口曲线变化规律。

中国古代宗族是一个封闭的血缘团体，氏族活动主要围绕着家族来开展。通过氏族祠堂的修建、祭拜祖先等活动，使氏族成员获得归属感、同源性和亲切感。徽州居民呈聚居特征，形成了聚落规模，每个家庭都有一个甚至几个家谱，而且他们的祠堂很大。同样的，他们的家谱系统是清楚的，并且有许多分类，如总族谱、分族谱、通谱、支谱等，使成千上万种的族谱倍增，这是很复杂的。对于局外人来说，很难辨认清楚。徽州历史上有许多有名的氏族姓，其中最有名的就是汪、程、胡、黄、吴、王和李等。这些姓氏的分支广泛，分布在徽州6个县中，在各自强大的社会力量和经济实力中，为当地商业繁荣发展提供了强有力的保障［2］。

图5 法向加工误差与切线倾角的关系

图6 X向加工误差与切线倾角的关系

X向和Z向加工误差与切线倾角呈非线性关系，如图6、图7所示。切线倾角越大，X向加工误差越大，而Z向加工误差越小。对比图6和图7可知，只要刀尖半径存在，X向或Y向至少有一个方向存在加工误差。

X向和Z向加工误差与切线倾角呈非线性关系，如图6、图7所示。切线倾角越大，X向加工误差越大，而Z向加工误差越小。对比图6和图7可知，只要刀尖半径存在，X向或Y向至少有一个方向存在加工误差。

图7 Z向加工误差与切线倾角的关系

2.2 刀尖半径对加工误差的影响

法向加工误差是随对刀半径的增加而线性递增的。切线倾角α分别为15°、45°和60°时，切向加工误差e与刀尖半径R的关系如图8所示。当切线倾角一定时，刀尖半径对法向加工误差的影响系数不变。结合式(2)并对比图5可知切线倾角α=45°时，其影响系数最大，刀尖半径对法向加工误差的影响最大，且切线倾角α与45°的差异越大，其影响系数越小。

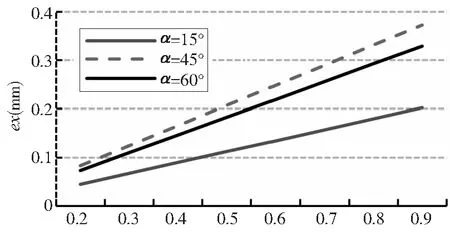
图8 法向加工误差与刀尖半径的关系

X向和Z向加工误差与刀尖半径也是线性递增关系，即切线斜角一定时，刀尖半径越大，X向和Z向加工误差越大。限于篇幅，其关系图在此不再给出。

综上分析，切削端面或圆柱面时，即α=0°或α=90°，法向加工误差为零，但存在X向或Y向误差；切削圆柱面或曲面时，即0°<α<90°，法向、X向和Z向误差均存在。在加工切线倾角接近于45°的圆锥面时，选用较小的刀尖半径，可减小加工误差，提高零件的形状精度。加工圆弧面、圆角等曲面时，其切线倾角随加工位置变化而变化，法向、X向和Z向三类误差均在变化，因此应根据加工零件的具体形状及加工要求具体问题具体分析。

3 刀尖半径误差对车削质量的影响

由刀尖半径引起的零件加工误差随切线倾角和刀尖半径的变化而变化，这种加工误差不仅对零件加工精度有影响，还对零件形状有影响，且对不同被加工表面的影响不同。

3.1 加工误差对端面或圆柱面的影响

车削端面时，数控系统控制车刀的假想刀尖点从端点G进给到中点H点，但实际切削点只是进给到A点，会残留圆锥状尾角。这种误差可以通过刀具半径补偿消除。

图9 车削端面或圆柱面

车削圆柱面时，会存在一个半径为R的切削圆角，且该形状误差无法消除，只能选用刀尖圆弧半径较少的车刀减小误差。

3.2 加工误差对圆锥面的影响

车削圆锥面时，切线倾角是圆锥面的锥角一半，X向、Z向和法向加工误差均存在，其误差值可按式(4)、(5)和(6)计算获得，如图10所示。与系统真正诉求的圆锥面相比，实际加工的圆锥会略短和略粗。车削加工时，这种误差在X向进行刀具补偿予以消除，其补偿量按式(5)计算。

图10 车削圆锥面

3.3 加工误差对曲面的影响

车削曲面时，切线倾角随着实际切削点处的曲率变化而变化，若不考虑车刀圆弧半径磨损等因素，X向、Z向和法向加工误差也是随着切削处的曲率变化而变化。由于法向加工误差随着切线倾角呈下开口圆锥曲线关系，且切线倾角在45°时，法向加工误差最大，因此对于车削凸圆弧时，实际车削轮廓是比理论圆弧略大的椭圆圆弧。如图11所示，圆弧APB是系统真正诉求的加工轮廓，而实际加工轮廓为曲线AQB。

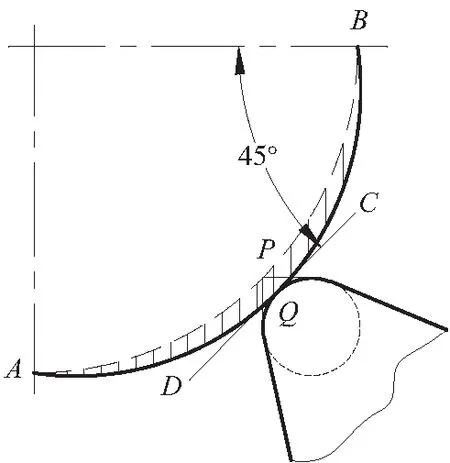
图11 车削凸圆弧

值得注意的是，虽然存在X向和Z向加工误差，若圆弧起点处的切线倾角是90°时，则起点处的Z向误差为零，而X向误差等于车刀的圆弧半径R；若圆弧终点处的切线倾角是0°时，则起点处的Z向误差为车刀的圆弧半径R，而X向误差为零。在实际车削加工中，应根据曲线实际情况和加工具体要求区分处理。车削凹圆弧时，实际车削轮廓也是一条比理论圆弧略大的椭圆圆弧，如图12所示。

图12 车削凹圆弧

综上分析可见，车刀刀尖圆弧引入的加工误差对加工质量的影响较为复杂，不同的待加工形状和不同的车刀圆弧其加工误差不同。在进行数控车削编程时，应根据具体的加工要求和工件形状具体问题具体分析，合理补偿车刀刀尖圆弧误差。

4 小结

由于车刀刀尖圆弧半径的存在，在实际车削点处的X向、Z向和法向等三个方向至少存在一个方向的加工误差，且对加工质量的影响较为复杂。

(1)随着切线倾角的增大，法向加工误差按下开口圆锥曲线的变化规律先增大后减小，X向加工误差

非线性递增，Z向加工误差非线性递减。随着刀尖圆弧半径增加，三个方向的加工误差均是线性递增的。

(2)车刀刀尖半径引入的加工误差对端面或圆柱面的加工形状没有影响，但也存在X向或Z向加工误差，对待加工表面的尺寸精度有影响；加工圆锥面或曲面时，三个方向的加工误差均存在，既影响被加工件的形状精度，也影响被加工件的尺寸精度。

(3)X向、Z向和法向加工误差均与切线倾角和刀尖圆弧半径有关，应根据具体情况合理补偿车刀刀尖圆弧误差，提高车削加工精度。

[1] 周建来，张南乔，刘树春.数控车削系统刀尖半径补偿模型[J].农业机械学报，2008,39(12):187-190.

[2] 朱建军，唐佳，赵中华.车削刀片刀尖圆角半径对加工的影响[J].实验室研究与探索,2012,31(10):254-257.

[3] 吴志清.数控车刀刀尖圆弧半径引起的误差分析[J].煤矿机械,2009,30(2):125-127.

[4] 杨锦涛. 数控车削中刀尖半径对零件轮廓的影响及解决方法[J]. 机械工程与自动化,2011,166(3):195-196.

[5] 徐丽霞， 凌莉， 邓小民，等. 数控切削过程刀尖圆弧半径的误差与补偿分析[J].机械工程师，2016(1)：37-38.

[6] 李英平. 基于FANUC0iT系统刀尖圆弧半径补偿与刀具磨耗补偿[J].组合机床与自动化加工技术，2009(4)：79-81.

[7] 高晓东. 数控车削刀具刀尖圆弧半径对加工精度影响的分析与解决途径[J].机床与液压,2013,41(14):145-147.

[8] 殷小清，王 阳. 数控车削加工刀尖圆弧半径补偿功能的建立[J].装备制造技术，2015(7)：223-226.

[9] 许光彬.数控车削刀尖半径补偿与加工误差分析[J].重庆科技学院学报(自然科学版),2012,14(4):126-128.

(编辑 李秀敏)

The Effect of CNC Lathe Tool Nose Radius on the Turning Quality

WANGShou-zhi，HANJin-yu

(TianjinSino-GermanCollegeofAviation,AerospaceandAutomobile,UniversityofAppliedSciences,Tianjin300350，China)

ThemachiningerrorsmodelandalgorithminXdirection,ZdirectionandthenormaldirectionwaspresentedaccordingtothegeometryrelationshipoftheCNCturningtoolandmachinedsurface.Thentheinfluencefactorsofthemachiningerrorandtherelationshipbetweenthemachiningerrorsandtangentangle,noseradiuswereanalysed,andtheinfluenceofdifferentdirectionerrorsonthequalityofturningisanalyzed.TheanalysisshowsthatprocessingerrorinXdirection,Zdirectionandthenormaldirectionwillgenerateduetothepresenceoftoolnoseradius.Theseerrorsincreasewiththeincreaseoftoolnoseradius,andthereisamonotonenonlinearrelationbetweenthetangentangleandXdirectionerrororZdirectionerror,adownwardcurverelationbetweenthetangentangleandnormaldirectionerror.Eachdirectionerrorwillinfluencetheshapeanddimensionalaccuracyoftheparts,anddifferentshapeoftheparthasdifferenteffects.

turningtool;roseradius;turningquality;effect

1001-2265(2016)12-0125-04DOI:10.13462/j.cnki.mmtamt.2016.12.034

2016-02-22；

2016-03-21

王守志(1977—)，男，山东邹城人，天津中德应用技术大学副教授，博士，研究方向为智能化检测与监控，(E-mail)564362468@qq.com。

TH17；TG

A