三点弯曲下混凝土断裂性能参数试验研究
2016-02-05陈红鸟赵艳兵孙敬明
刘 春,陈红鸟,赵艳兵,孙敬明,才 琪
(贵州大学空间结构研究中心,贵阳 550003)
三点弯曲下混凝土断裂性能参数试验研究
刘 春,陈红鸟,赵艳兵,孙敬明,才 琪
(贵州大学空间结构研究中心,贵阳 550003)
采用三点弯曲试验对混凝土断裂性能参数进行研究,测试了一系列尺寸相同、强度不同的预制切口梁。通过采用等效裂缝模型和双参数模型确定混凝土的断裂韧度,结果表明:采用等效裂缝模型和双参数模型计算的混凝土断裂参数基本相同;随着抗压强度的增加,断裂韧度呈上升趋势,通过曲线拟合,提出根据抗压强度确定断裂韧度的经验公式。通过对试验荷载-挠度曲线进行三种不同的处理,包括国际材料和结构实验室联合会(RILEM)建议、对曲线尾部进行延伸以及采用实际的曲线,得到基于虚拟裂缝模型的断裂能。结果表明,RILEM建议得到的断裂能偏大,当曲线下降段的最低荷载与峰值荷载比值Pmin/Pc≤0.04时,采用实际荷载-挠度曲线得到的断裂能与尾部延伸后曲线得到的断裂能误差小于5%,可为实际断裂试验的实施提供参考。
三点弯曲; 素混凝土; 抗压强度; 断裂韧度; 断裂能
1 引 言
自从1961年Kaplan[1]把断裂力学理论引入混凝土结构,混凝土断裂理论的研究和应用引起了国内外学者的普遍关注。能量场的断裂能和应力场的断裂韧度作为衡量混凝土断裂性能的重要参数,是研究混凝土断裂力学的关键。要确定这两个断裂性能参数,一般采用RILEM建议的三点弯曲法。一些研究[2-4]表明强度是影响混凝土断裂能的主要因素,混凝土断裂能随强度等级的提高而增加,并给出断裂能GF关于抗压强度fcu的拟合经验公式;也有研究[5-6]认为混凝土的断裂能与抗压强度没有直接关系。然而有研究[7-9]表明,由三点弯曲法测得的断裂能存在误差和尺寸效应,产生误差及尺寸效应的原因在于对荷载-挠度曲线尾部的处理。本文通过对荷载-挠度曲线尾部的三种不同处理方法,计算断裂能并进行对比分析。对比结果表明:采用RILEM建议的方法得到的断裂能数值偏大;由于断裂面曲折度的影响,断裂能与强度的关系不大。针对混凝土断裂韧度的计算有多种模型,主要包括等效裂缝模型[10]、双参数模型[11]、双K断裂模型[12]和新KR阻力曲线模型[13-14]等。赵艳华等[15]对双参数模型和尺寸效应模型得到的阻力曲线进行了对比分析,宣方龙[16]、马颖利[17]对双参数模型和双K断裂模型进行对比研究,许成祥等[18]、张廷毅等[19]、贾艳东[20]对影响混凝土断裂韧度的因素(如骨料类型、强度等级、龄期、相对切口深度、粗骨料最大粒径、水灰比等)进行讨论。本文通过采用等效裂缝模型和双参数模型得到混凝土I型断裂的断裂韧度KIc,并对两种模型得到的断裂参数进行对比分析。结果表明:两种模型得到的断裂参数非常接近。KIc随抗压强度fcu增长而增大,本文给出KIc关于fcu的线性经验公式,可为工程实践提供参考。
2 试 验
2.1 材料和配合比
试验采用的试件尺寸如表1所示,试验用混凝土的配合比和立方体抗压强度如表2所示。水泥采用波特兰水泥、细骨料为天然河沙、粗骨料为碎花岗岩,最大骨料粒径Dmax=10mm。根据混凝土强度等级共浇筑C30、C40、C60、C80、C90五组试件,每组浇筑六条梁,四个立方体试块和四个圆柱体试块,预制切口梁试件尺寸(跨度、高度、厚度、预制切缝长度和宽度)依据RILEM[21-23]提出的建议设计,梁的尺寸为:710mm×150mm×70mm,跨度为600mm。预制切口的深度为60mm,预制切口的宽度为2mm。每个立方体试件的尺寸为:150mm×150mm×150mm,每个圆柱体试件的尺寸为:φ150mm×300mm。试块浇筑后,在自然条件(温度:(20±2) ℃;相对湿度:75%~85%)下养护至28d。依据《 普通混凝土力学性能试验方法标准》(GBT50081-2002)[24],立方体进行抗压强度试验确定立方体抗压强度fcu,圆柱体进行压缩试验确定混凝土的杨氏模量E和劈裂试验确定抗拉强度ft。
2.2 试验装置
本试验采用50kNMTS设备对混凝土梁进行三点弯曲试验,试验示意图如图1(a)所示。试验采用闭环伺服液压控制系统,试验装置图如图1(b)。为了较好的控制试件裂纹扩展,采用位移控制法,加载速率为0.2mm/15min。大概在6~8min可以加载到极限荷载。通过在梁预制切口端部放置夹式位移计测量裂缝口张开位移(CMOD),通过在跨中安装竖向线性位移传感器(LVDT)测量梁的跨中挠度 ,数据记录仪记录下了全过程的荷载-挠度曲线。
试验中,在试件梁与支座之间放置石膏浆体,填充由于试件梁表面粗糙造成的梁与支座之间的间隙,再施加0.2kN的力,使试件梁与支座完全接触,消除它们之间的虚位。通过将位移计LVDT固定在梁支座上,使位移计与梁支座共同移动,可以消除二者之间的相对刚性位移带来的误差。
根据记录的荷载-挠度曲线如图1(c),读取极限荷载和对应的挠度,从而计算出了断裂韧度。根据等效裂缝模型由荷载挠度曲线可以得到断裂能。

表1 试件尺寸
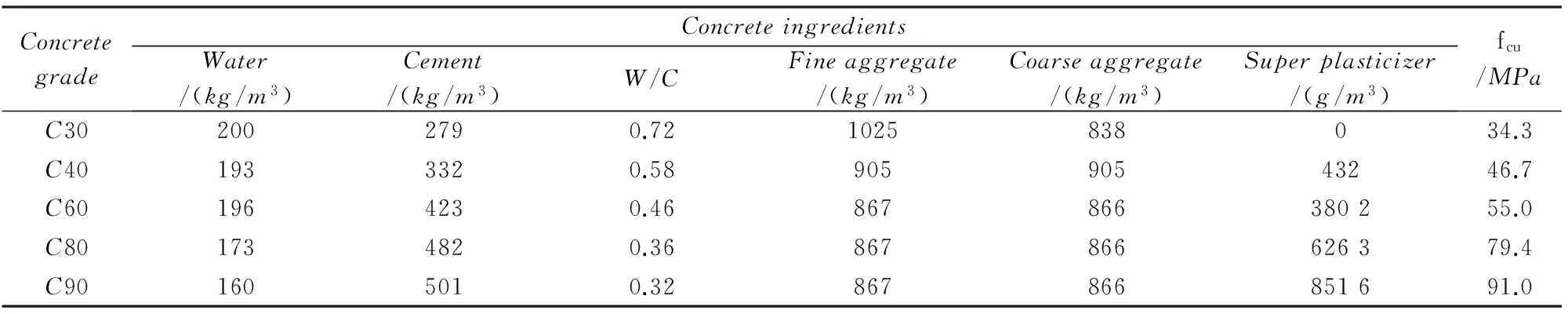
表2 混凝土配合比和立方体抗压强度
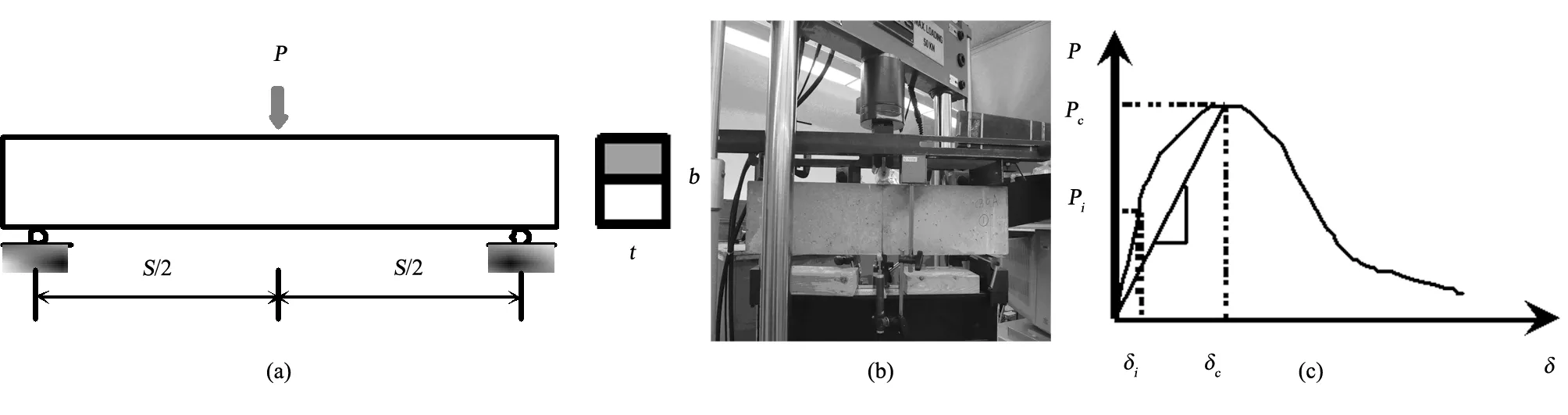
图1 (a)三点弯曲试验示意图;(b)试验装置图;(c)荷载-挠度曲线Fig.1 (a)Three-point bending beam;(b)experimental setup;(c)load-deflection curve
3 理论背景
3.1 断裂韧度KIc的计算
断裂韧度KIc代表裂缝扩展所需要的应力强度临界值,可采用Karihaloo和Nallathambi[10]提出的等效裂缝模型或Jenq和Shah[11]提出的双参数模型求得。等效裂缝模型基于荷载-挠度曲线来计算断裂韧度,该模型认为带切口三点弯曲梁在上升段的非线性阶段(也称为裂缝“亚临界发展”阶段)刚度的下降完全是由断裂过程区发展引起的。该模型在混凝土梁中引入了一个虚拟裂缝,虚拟梁的临界裂缝长度为ae,而实际梁的真实初始裂缝长度为a0。
从图1(c)中荷载-挠度曲线的线弹性段取一点(Pi,δi),将该点代入公式(1)就可以求出初始弹性模量E:
(1)
E是初始弹性模量,S、b和t分别是梁的跨度、高度和厚度,q是梁单位长度的自重。
其中F1(α0)函数如下:
(2)
式中,α0=a0/b,Y(x)是三点弯曲梁的几何因子,由下式确定:
(3)
或等于
(4)
为了求断裂韧度KIc,需要先求出临界裂缝长度ae。极限荷载Pc和与之对应的挠度δc能够由ae表示如下
(5)
将公式(2)中的α0换成αe,函数F1(αe)变成
(6)
将荷载-位移曲线的峰值点(Pc,δc)代入公式(5),即可求出F1(αe)。再结合公式(6),求出积分上限αe=ae/b,就可以获得临界裂缝长度ae。
通过对大量的三点弯曲梁试验结果进行回归分析,Karihaloo[25]等给出了一个经验公式来确定临界裂缝长度ae:
(7)
式中,(σN)u=6Mmax/(tb2);Mmax=(Pmax+qS/2)S/4。对混凝土最大骨料粒径在2~20mm,初始逢高比在0.1~0.6,试件高度在100~400mm,γ1=0.088±0.004,γ2=-0.208±0.010,γ3=-0.451±0.013,γ4=-1.653±0.109。
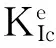
(8)
几何因子Y参见公式(3)或公式(4)计算。
公式(8)可通过下式进行修正[25]:
(9)
根据双参数模型[11],裂缝口张开位移可以如下计算:
(10)
其中
(11)
裂缝尖端张开位移:
(12)
其中
(13)
(14)
式中,Wb=WsS/L,Ws为梁的自重,L为梁的长度。F3(αe)是三点弯曲梁的另一几何因子,等于
(15)

(16)
脆性指数Q可以如下来确定:
(17)
脆性指数Q反映了材料的脆性,Q越小,材料越脆。
根据线弹性断裂准则和等效弹性裂缝模型,临界能量释放率GIc可以通过下式计算:
(18)
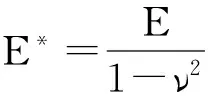
3.2 断裂能的计算
断裂能GF被定义为产生单位面积裂缝所需要的能量,是基于虚拟裂缝模型并考虑了混凝土软化特性的断裂参数。在虚拟裂缝模型中,产生新表面所需的能量与使断面分开所需的能量相比是可以忽略的。断裂能主要消耗在抵抗黏聚力上,根据RILEM[21]的建议,断裂能可以通过荷载-跨中挠度曲线计算出来。
计算断裂能时需考虑自重的影响,设MTS促动器施加的外荷载为Pa,梁自重等价为一附加集中荷载Pw,则总的荷载为P=Pa+Pw。如图2(a)所示,δ0是对应于Pa=0时的挠度,W0是P(δ)曲线和P=Pw包围的区域,W1=Pwδ0。

图2 断裂能计算示意图Fig.2 Calculating diagram of fracture energy
前期研究发现W2区域和W1几乎相等,因此每单位面积上的总断裂能可以如下计算:
(19)
钱觉时在文献[7-8]中对W2=W1提出质疑,认为对荷载-挠度曲线尾部W2的处理是产生误差及断裂能尺寸效应的重要原因,基于此,本文根据文献[8]中对尾部的处理方法,得到延伸后的荷载-挠度全曲线P(δ)*,积分面积如图2(b)所示。断裂能GF-N采用下式计算
(20)
本次试验得到了三点弯曲梁从加载到断裂的荷载-挠度曲线,测得的最终荷载较小,接近梁最终断裂破坏。若忽略尾部,对试验得到的荷载-挠度曲线直接进行积分可得到断裂能GF-P(δ),积分面积如图2(c)所示。
(21)
虚拟裂缝模型定义特征长度 lch为
(22)
其中ft是混凝土的抗拉强度。虚拟裂缝模型的特征长度lch反映了材料的脆性,lch越小,材料越脆。
4 试验结果
4.1 荷载-位移曲线
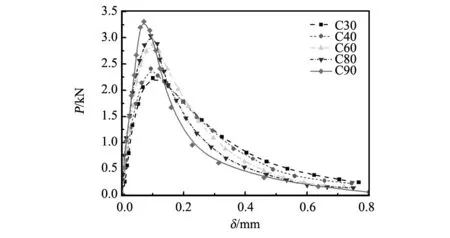
图3 荷载位移曲线Fig.3 Load-deflection curves
三点弯曲试验得到的荷载-挠度曲线如图3所示。试验结果表明,随着混凝土强度等级的提高,峰值荷载呈升高的趋势。混凝土强度越高,峰值荷载对应的挠度越小,荷载-挠度曲线的上升段和软化段越陡,这与文献[26]结果基本一致。峰值荷载主要是受混凝土的抗拉强度ft控制。随着混凝土强度等级的提高,混凝土的抗拉强度也呈上升趋势。跨中挠度主要受荷载P和抗弯刚度EI的影响。混凝土强度越高,E越大,虽然荷载也有提高,但趋势不如E大,导致位移减小,试件呈现更高的脆性。
4.2 断裂韧度
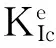


表3 等效裂缝模型计算的断裂参数

表4 由双参数模型确定的断裂参数

续表
4.3 断裂能
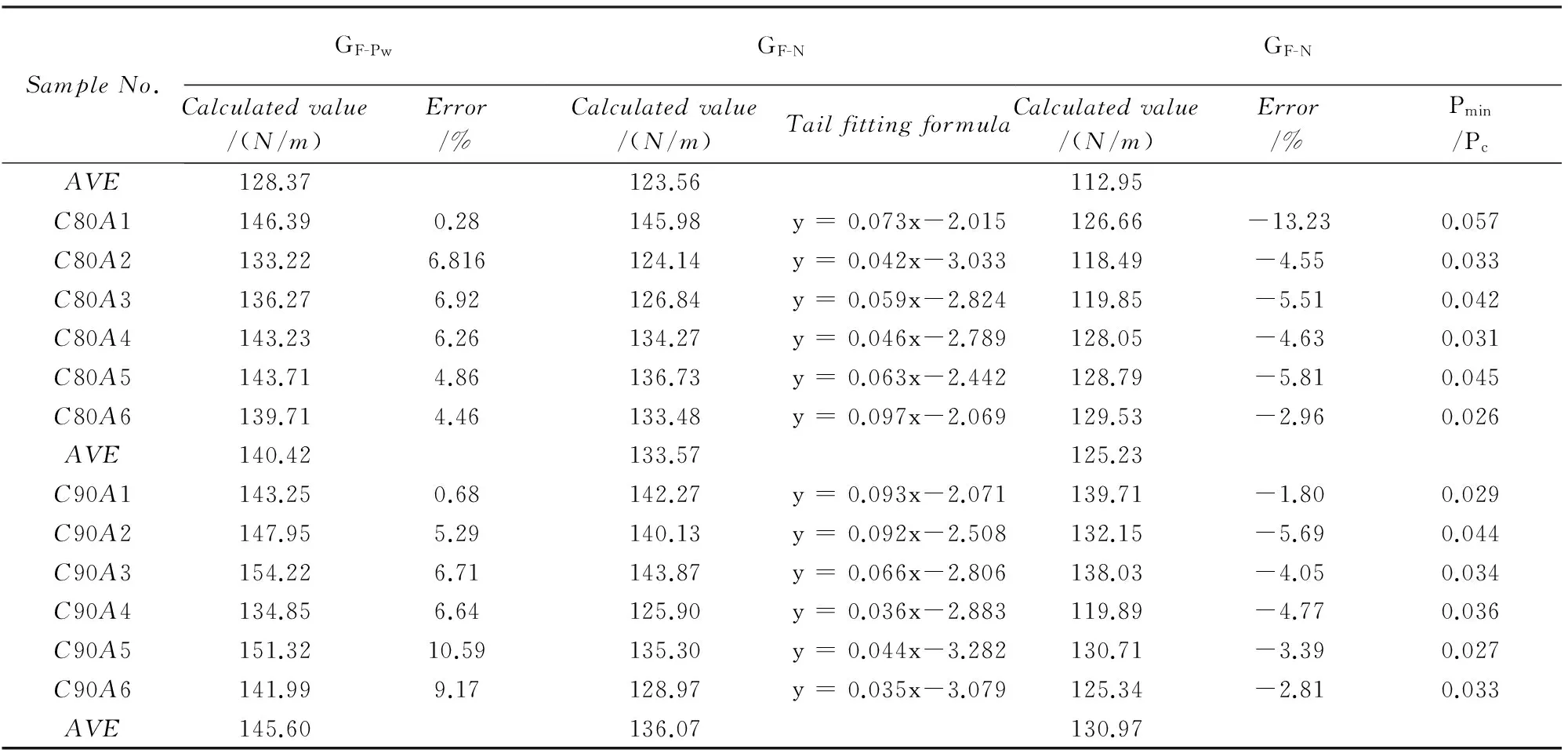
采用三种方法算得的断裂能如表5所示。对荷载-挠度曲线尾部的拟合参照文献[8]中的公式取y=C/xn(C和n为常数)。文献[8]指出:当n>2时,W2
对比GF-P(δ)和GF-N,GF-N>GF-P(δ),这是因为GF-N是对荷载-挠度曲线尾部拟合延伸后对曲线积分得到的结果。当荷载-挠度曲线下降段最低点荷载Pmin/Pc在0.03~0.04时,GF-P(δ)的误差在5%以下;当Pmin/Pc<0.01时,二者基本相等。也就是说,当最低点荷载与峰值荷载比值满足一定条件时,可以不用对曲线尾部进行拟合延伸处理,直接用试验测得的荷载-挠度的曲线计算断裂能就可以得到理想的结果。

表5 断裂能对比
续表
5 讨 论
5.1 断裂能的3种求解方法
文献[8]表明GF-Pw为GF-N当n=2时的特解,n偏离2越远,得到的断裂能误差将越大。当n=2时,GF-Pw是精确解;当n≠2时,GF-Pw是近似解。本次试验的结果表明,n在1.5~2.5之间时,GF-Pw偏离GF-N的误差在5%以内。由于试验之前无法保证测得的荷载挠度曲线尾部的拟合公式中n是否在1.5~2.5之间(本次试验30个试件中约有10个试件的n值在1.5~2.5之间),无法保证直接由GF-Pw得到的断裂能的误差在允许的范围内。因此由GF-Pw得到较精确的断裂能,需要对GF-Pw进行修正,或者采用其他方法计算断裂能。
采用GF-N得到的断裂能可被认为是断裂能的精确解。但是采用GF-N来计算断裂能,由于n值的不确定性,试验得到的每一条荷载挠度曲线都需要对尾部进行拟合,得到合适的n值,才能进一步得到断裂能,过程较为繁琐,不便于直接使用。
采用实际曲线获得的断裂能GF-P(δ),需要控制荷载挠度曲线下降段的最低点荷载Pmin在合适的范围内。本次试验表明只要把Pmin控制在极限荷载Pc的0.04以下,就可以得到误差允许范围内的结果,且Pmin/Pc越小,得到的结果越精确。当Pmin/Pc<0.04时,GF-P(δ)误差非常小(<5%),可以作为精确解。采用GF-P(δ)求断裂能要求试验得到荷载挠度曲线的稳定的下降段以及尽可能小的最低点荷载,这就对试验的装置仪器和试验操作提出了更高的要求,本次试验表明,现有的试验装置和仪器完全可以实现。
5.2 断裂韧度、断裂能与抗压强度的关系
混凝土断裂韧度、断裂能与抗压强度的关系曲线如图4所示。从图4(a)可以看出断裂韧度KIc随着抗压强度fcu的增加而增加,它们之间的关系大略如下:
KIc= 0.0081fcu+0.7969
(23)
KIc和fcu的单位分别是MPa·m1/2和MPa。拟合公式的相关系数r为0.7945,表现出一定的离散性。这种离散性主要是由混凝土的三相(水泥砂浆、骨料、过渡带)结构组成引起的材料不均匀性、试件的个体差异以及试验中的误差造成的。试验中采集到的C90混凝土的6条荷载挠度-位移曲线如图4(b)所示,可以发现荷载-位移曲线具有一定离散性,由此曲线得到的应力场断裂参数-断裂韧度KIc也必然具有一定离散性。
断裂能GF随着抗压强度fcu变化趋势不是很明显,如图4(c)所示。由表3可知,C30、C40、C60的断裂能平均值接近于123MPa·m1/2,C80、C90时GF略有提高,大约为135MPa·m1/2,因此笔者认为混凝土的强度等级对断裂能影响较小。
文献[6]认为抗压强度不是一个能较好描述高性能混凝土断裂能变化的参数,这是由于混凝土技术的发展而使配置高性能混凝土时采用较低的水胶比并采用活性掺和料。水胶比的降低和活性掺和料的掺入,改善了硬化水泥浆与粗集料的界面强度,导致混凝土裂缝扩展模式从绕过粗集料扩展向横穿粗集料扩展过渡。因此高强度的混凝土断裂时,裂缝直接从粗骨料穿过,导致裂缝路径的曲折度较小,骨料之间的咬合力降低;而低强度的混凝土断裂时,裂缝面绕过骨料开裂,裂缝路径曲折度较大,骨料之间的咬合作用较强;中强度的断裂面曲折程度和骨料咬合力介于高强度混凝土和低强度混凝土之间。综合各因素导致断裂能随抗压强度略有提高,但增大趋势并不明显。
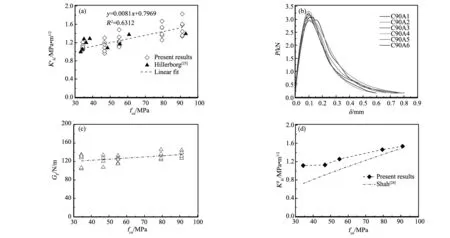
图4 断裂能和断裂韧度Fig.4 Fracture energy and fracture toughness(a)comparisons of present results and hillerborg's results;(b)load-deflection curves of C90 concrete beams;(c)effects of the compressive strength on;(d)comparisons of present results and shah's empirical formula
5.3 断裂韧度对比分析
6 结 论
本文采用RILEM提议的三点弯曲试验对素混凝土的断裂性能进行科学研究。通过试验得到了荷载-挠度曲线,进而计算了混凝土I型断裂的断裂能GF和断裂韧度KIc,对比分析得到以下结论:
(1)通过三点弯曲试验得到了不同强度混凝土的典型荷载位移曲线,随着强度等级的提高,由于混凝土的抗拉强度ft提高,峰值荷载有所增大,但由于弹性模量E的增大,刚度变大,使与峰值荷载对应的跨中挠度降低;
(2)通过对比不同计算方法得到的断裂能,发现荷载挠度曲线尾部的处理对断裂能的计算结果有较大影响。采用RILEM推荐的公式得到的断裂能比实际值偏大,误差最大时可以达到11.8%。当Pmin/Pc较大时,建议对尾部进行处理来计算断裂能,当Pmin/Pc较小时(如当Pmin/Pc<0.04,误差在5%以内),可以直接利用试验测得的曲线来计算断裂能;
(3)断裂韧度KIc随抗压强度的增大而增大;断裂能GF与抗压强度fcu的关系不大。由于高强度的混凝土断裂面曲折度较小,骨料之间的咬合力较低;而低强度的混凝土裂缝路径曲折度较大,骨料之间的咬合作用较强,导致断裂能GF随抗压强度fcu的变化关系不明显;
(4)将等效裂缝模型和双参数模型计算的断裂韧度KIc进行对比,发现两者计算的结果基本相等,与Karihaloo的结论相符。等效裂缝模型的结果与Karihaloo的结果相符;有研究表明断裂韧度随骨料粒径的增加呈增大趋势,由于本次试验采用的骨料粒径比Shah等的试验大一倍多,所以我们采用双参数模型得到的结果比Shah的经验公式值偏大。
[1]KaplanMF.Crackpropagationandthefractureofconcrete[J].Journal of the American Concrete Institute,1961,58(5):591-610.
[2] 鲁丽华,吴 卓,于 飞,等.不同强度及粗骨料对混凝土断裂能影响的实验研究[J].北方交通,2006,(06):58-60.
[3] 吴科如.轻集料混凝土的断裂能[J].三峡大学学报(自然科学版),2002,(01):9-11.
[4]WittmannFH,RoelfstraPE,MihashiH,etal.Influenceofageofloading,water-cementratio,andrateofloadingonfractureenergyofconcrete[J].Materials and Structures,1987,116(20):103-110.
[5] 严 安,吴科如,姚 武,等.混凝土材料的真实断裂能研究[J].建筑材料学报,2001,(04):346-350.
[6] 严 安,吴科如,姚 武,等.混凝土的断裂能随断裂路径的变化规律[J].水利学报,2002,(01):76-80.
[7] 钱觉时,范英儒,袁 江.三点弯曲法测定砼断裂能的尺寸效应[J].重庆建筑大学学报,1995,(02):1-8.
[8] 钱觉时.论测定断裂能的三点弯曲法[J].混凝土与水泥制品,1996,(06):20-23.
[9] 张 东,刘娟淯,陈 兵,等.关于三点弯曲法确定混凝土断裂能的分析[J].建筑材料学报,1999,(03):206-211.
[10]KarihalooBL,NallathambiP.Effectivecrackmodelforthedeterminationoffracturetoughnessofconcrete[J].Engineering fracture Mechanics,1990,35(4-5):637-645.
[11]JenqYS,ShahSP.Twoparameterfracturemodelforconcrete[J].Journal of Engineering Mechanics,1985,111(10):1227-1241.
[12] 徐世烺,赵国藩.混凝土结构裂缝扩展的双K断裂准则[J].土木工程学报,1992,(02):32-38.
[13]ReinhardtHW,XuSL.Crackextensionresistancebasedonthecohesiveforceinconcrete[J].Engineering Fracture Mechanics,1999,64:563-587.
[14]XuSL,ReinhardtHW.Crackextensionresistanceandfracturepropertiesofquasi-brittlesofteningmaterialslikeconcretebasedonthecompleteprocessoffracture[J].International Journal of Fracture,1998,92(1):71-99.
[15] 赵艳华,魏 鹏,高洪波.混凝土双参数断裂模型和尺寸效应模型R阻力曲线比较[J].大连理工大学学报,2015,(04):387-392.
[16] 宣方龙.混凝土双参数和双K参数模型的比较研究[D].大连:大连理工大学,2002.
[17] 马颖利.试验研究混凝土双参数模型和双K断裂准则[D].大连:大连理工大学,2002.
[18] 许成样,戴绍斌,李继祥.三点弯曲梁的混凝土断裂韧度计算[J].江汉石油学院学报,1995,(01):102-105.
[19] 张廷毅,高丹盈,郑光和,等.三点弯曲下混凝土断裂韧度及影响因素[J].水利学报,2013,(05):601-607.
[20] 贾艳东.不同粗骨料及强度等级混凝土的断裂性能及其实验方法研究[D].大连:大连理工大学,2003.
[21]RILEMCommitteeFMC50.Determinationofthefractureenergyofmortarandconcretebymeansofthethree-pointbendtestsonnotchedbeam[J].Materials and Structures,1985,18: 285-290.
[22]RILEMCommitteeFMT89.DeterminationoffractureparametersandCTODcofplainconcreteusingthree-pointbendtests[J].Materials and Structures,1990,23:457-460.
[23]RILEMCommitteeFMT89.Sizeeffectmethodfordeterminingfractureenergyandprocesszonesizeofconcrete[J].Materials and Structures,1990,23:461-465.
[24]GB50081-2002,普通混凝土力学性能试验方法标准[S].
[25]KarihalooBL.Fracturemechanicsandstructuralconcrete[R].England:Longman.Scientific&Technical,1995.
[26] 栾曙光,DavidD.混凝土断裂能GF随龄期、强度的变化规律[J].水利学报,1999,10:29-32.
[27]KarihalooBL,NallathambiP.Notchedbeamtest:ModeIfracturetoughness[A].FractureMechanicsTestMethodsforConcrete[C].London:Chapman&Hall,1991:1-86.
[28]JohnR,ShahSP.Fracturemechanicsanalysisofhigh-strengthconcrete[J].Journal of Materials in Civil Engineering,1989,1(4):185-198.
Experimental Study on Fracture Properties of Concrete Basedon Three Point Bending Tests
LIU Chun,CHEN Hong-niao,ZHAO Yan-bing,SUN Jing-ming,CAI Qi
(SpaceStructuresResearchCenter,GuizhouUniversity,Guiyang550003,China)
Aseriesofpre-notchedconcretebeamswiththesamegeometricsizesanddifferentcompressivestrengthsweretestedbyusingthreepointbendingteststoinvestigatethefracturepropertiesofplainconcrete.ThefracturetoughnessofconcretewasdeterminedbyusingtheEquivalentFractureModelandtheTwoParameterFractureModel.Analyticalresultsindicatedthatthefractureparametersdeterminedbythesetwomodelswereclose.Thefracturetoughnessincreasedastheincreaseofcompressivestrengthofconcrete.Empiricalformulawasbuilttodeterminethefracturetoughnessbyusingthecompressivestrength.Thefractureenergiesweredeterminedfromtheexperimentalload-deflectioncurvesviathreemeans,includingtheproposalsrecommendedbyRILEM,tailextensionofthecurvesbycurvefittingandtheactualcurves.TheresultsshowedthatfractureenergiesobtainedbyRILEMrecommendationwerehigherthanthatobtainedbytheothertwomethods.Whentheratioofthelowestloadatthedescendingpartofthecurvetothepeakload(Pmin/Pc)waslowerthan0.04,theerrorsofthefractureenergiesobtainedbytheactualload-deflectioncurvesandthatobtainedbytheextendedcurvewerelessthan5%,whichcouldprovideareferencefortheimplementationofthefracturetests.
threepointbending;plainconcrete;compressivestrength;fracturetoughness;fractureenergy
国家自然科学基金(51408144);贵州大学人才引进基金项目(201301);贵州大学研究生创新基金(2016001)
刘 春(1990-),男,硕士研究生.主要从事混凝土断裂力学方面的研究.
陈红鸟,博士,副教授.
TU
A
1001-1625(2016)12-4191-10
