多级评分的认知诊断计算机化适应测验*
2016-02-01涂冬波
蔡 艳 苗 莹 涂冬波
(江西师范大学心理学院, 江西师范大学心理健康教育研究中心, 江西省心理与认知科学重点实验室, 南昌 330022)
1 引言
认知诊断(cognitive diagnosis, CD)技术是认知心理学与心理计量学(Psychometrics)相结合的产物,它不仅要对个体心理特质水平进行宏观层次评价,还对个体心理内部加工过程进行诊断, 揭示个体的认知加工特点。它在诊断个体心理加工机制与相应机制是否一致或存在缺陷、诊断精神紊乱(psychiatry disorder)、诊断学生知识结构等方面具有重大意义,更为有效地揭示人类认知的过程及其心理学意义,从而更好地为指导教育教学决策和建构心理理论服务。计算机化适应测验(computerized adaptive testing, CAT)是一种全新的测试形式, 它采用“因人施测”、“量体裁衣”式的测试策略, 由计算机根据考生当前作答情况, 智能化从题库中挑选与考生相匹配的试题, 从而达到试题与考生水平的自适应(adaptive)。CAT能比传统纸笔测验更为高效、准确、可靠地评定考生水平, 国际上许多大型测验正在大力推行。
认知诊断计算机化适应测验(cognitive diagnosis computerized adaptive testing, CD-CAT)是将认知诊断基本理论、方法与计算机化自适应测验结合起来的产物, 由计算机(或internet)智能化且高效、快速和准确地实现对被试的认知诊断, 从而有利于认知诊断更好地服务实践。CD-CAT因充分结合了认知诊断和计算化自适应测验的双重优点而深受国内外研究者推崇。然而, 当前国内外关认知诊断计算机化自适应测验研究(如Kaplan, de la Torre, & Barrada,2015; Chen, Liu, & Ying, 2015; Wang, 2013; Hsu, Wang,& Chen, 2013; Mao & Xin, 2013; Wang, Chang, &Huebner, 2011; Cheng, 2009; 涂冬波, 蔡艳, 2015;郭磊, 郑蝉金, 边玉芳, 2015; 汪文义, 丁树良, 宋丽红,2014; 涂冬波, 蔡艳, 戴海琦, 2013; 陈平, 辛涛,2011)都是针对0-1评分的测量数据的CD-CAT, 而关于多级评分CD-CAT (polytomously scored CD-CAT,psCD-CAT)的研究国内外几乎还未开展; 然而, 在教育与心理测量中, 存在大量的多级评分测量数据,如表现性测验、教育成就测验中的主观题以及心理学中的Likert型量表等均为多级评分数据, 而这时传统0-1评分的CD-CAT显然不适用, 因此多级评CD-CAT亟待深入, 以进一步推动认知诊断和计算机化自适应测验更好地服务实际。查阅相关文献,我们只发现一篇关于多级评分CD-CAT的报道(周婕,丁树良, 陈平, 2007), 周婕等人(2007)的研究中采用先认知诊断后能力估计的方式进行, 但该方法并未真正使用多级评分认知诊断模型来处理多级评分的CD-CAT, 而是采用传统IRT下等级反应模型及0-1评分的规则空间方法来处理。总体来看, 国内外关于多级评分的CD-CAT研究十分薄弱, 有待开展。
本文主要在0-1评分CD-CAT基础上, 探讨多级评分认知诊断计算化适应测验(psCD-CAT)的算法与技术, 涉及psCD-CAT多级评分认知诊断模型拓展、选题策略开发、参数估计算法、终止策略以及多级评分认知诊断模型的拓展等, 并重点探讨psCDCAT的设计思路及其合理性与实现, 为进一步拓展CD-CAT在实践中的应用提供方法和实践支持。
2 多级评分认知诊断计算机化自适应测验设计
2.1 多级评分的认知诊断模型
涂冬波、蔡艳、戴海琦和丁树良(2010)基于Samejima (1995, 1997)的等级反应模型(GRM)开发了多级评分的DINA模型——P-DINA模型, 该模型项目反应函数为:
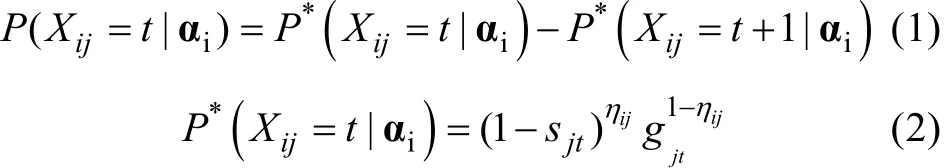
P-DINA模型中, 理想反应得分(ideal response score, IRS)ηij沿用了0-1评分DINA模型中计算公式, 即,取值只有0和1两种; 同时,公式2中满足。他们研究发现, P-DINA模型具有较好的参数估计精度及属性诊断正确率, 这为拓展多级评分数据的认知诊断提供了重要的方法支持。关于P-DINA模型的详细介绍, 感兴趣读者可参考该文献。
在涂冬波等人(2010)研究基础上, 我们对P-DINA模型做了进一步拓展(拓展后的模型记为GP-DINA模型), 具体为:将P-DINA模型中的理想反应得分ηij从0-1评分拓展为多级评分, 从而实现观察得分与理想得分均为多级评分的对应, 多级理想反应得分ηij的计算公式为:

公式3中,mfj为项目j的满分值,部分为被试掌握属性的百分比。被试在项目上的理想得分ηij等于被试掌握项目测量属性的百分比乘以该题满分值。由于该理想得分有小数, 因此为了便于理解, 可以对ηij取整。实际上, 对于我们提出的算法(见下公式6),ηij取整与不取整是等价的, 不影响GP-DINA模型的表达与计算。
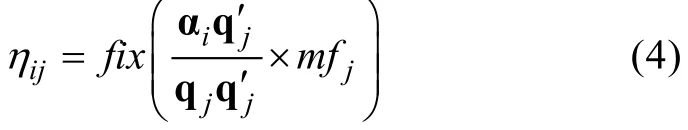
结合公式4, 则公式2可以转换为:

以上公式4、5及结合公式1即GP-DINA模型的项目反应概率函数。与P-DINA模型相比,GP-DINA模型只是拓展了理想反应得分ηij的计算方法, 从0-1记分的ηij拓展为多级计分的ηij, 其余的参数解释和意义与P-DINA模型一样。现举例加于说明P-DINA模型与GP-DINA两个模型的差异:假设某项目且该题满分mfj=3, 则两个模型被试得分概率如下:

表1 两个多级评分模型的区别
表1可知, 在同等条件下, P-DINA模型只能将被试的项目反应概率区分为两类, 而拓展后的GP-DINA模型可以将被试的项目反应概率区分为(mfj+ 1)类(表1中可以区分出4类被试); 因而, 与P-DINA模型相比, GP-DINA模型可以区分出更多类型的被试, 从而提供的信息更为细致和丰富; 同时, GP-DINA模型中, 当ηij=0时被试得0分的概率倾向最大, 当ηij=1时被试得1分的概率倾向最大, 当ηij=2时被试得2分的概率倾向最大, 当ηij=3时被试得3分的概率倾向最大(具体详见表1中的阴影部分), 从而实现了多级的观察得分与多级的理想得分的间对应关系; 而P-DINA模型中, 被试得分概率较大的均集中在0分和满分两个极端, 因此P-DINA倾向于将被试得分两极化, 而难于区分得中间分数段的被试。因而GP-DINA模型克服了P-DINA模型只能处理“0分向满分或满分向0分滑动”缺陷。同时, 我们采用Monte Carlo模拟研究发现:在相同条件下, GP-DINA模型不论是在项目参数还是被试参数上比P-DINA模型具有更高估计精度; 如当6个独立属性题量为60题时, P-DINA模型的模式判准率为80.7%, 而GP-DINA模型则高达95.5% (限于篇幅, 这里未全部列出, 感兴趣的读者可以向作者索要GP-DINA模型参数估计程序及Monte Carlo模拟研究结果)。
2.2 多级评分CD-CAT (psCD-CAT)参数估计算法
CD-CAT框架下, 参数估计一般指被试参数的条件估计, 即在题库项目参数已知的条件下来估计被试参数。目前在CD-CAT中, 常用被试参数估计方法主要有3种算法(Huebner & Wang, 2011; Feng, Habing, &Huebner, 2014):极大极大似然估计法(Maximum Likelihood Estimation, MLE), 极大后验估计法(Maximum a Posteriori, MAP)和期望后验估计法(Expected a Posteriori, EAP), 它们都是在项目参数已知的条件下来估计被试的知识状态(Knowledge States,KS)或属性掌握模式。

则多级评分认知诊断模型——GP-DINA模型的似然函数为,

则被试i的知识状态的极大似然(MLE)估计值为,
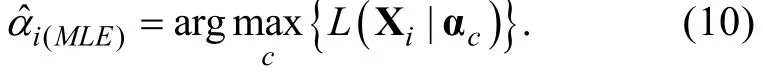
即MLE是指使似然函数(见式9)具有最大值所对应的知识状态作为被试知识状态的估计值。
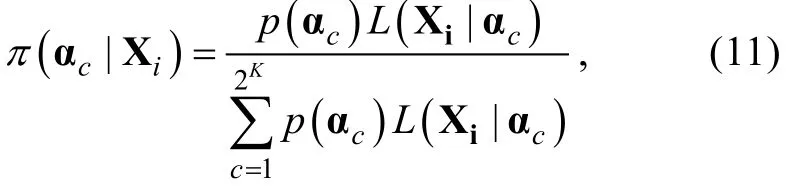
那么, 被试i的知识状态的极大后验(MAP)和期望后验(EAP)估计值分别为:

即MAP指在给定作答向量Xi条件下具有最大后验概率的知识状态作为被试知识状态的估计值; EAP是以被试知识状态的后验期望值作为估计值。
2.3 多级评分的CD-CAT选题策略
CD-CAT通常是根据信息量来选择最适合被试作答的项目, 由于知识状态的非连续性, 当前CD- CAT环境下主要是根据Kullback -Leibler信息量指标进行选题, 常用的方法有KL信息量(Kullback -Leibler),PWKL信息量(Posterior-Weighted KL), HKL信息量(Hybrid KL)等(Cheng, 2009; Hsu et al., 2013)。但以上选题策略均是在0-1评分的CD-CAT基础上提出来的, 因此对于多级评分的CD-CAT需要对以上算法进行多级评分拓展, 本文把多级评分拓展后的选题策略分别记为PS-KL、PS-PWKL和PS-HKL, 其多级评分拓展后计算公式分别如下:

PS-PWKL信息量(Posterior-Weighted KL)是考虑后验概率加权的PS-KL信息量, 若记是知识状态为的后验概率计算公式参见2.8), 则,
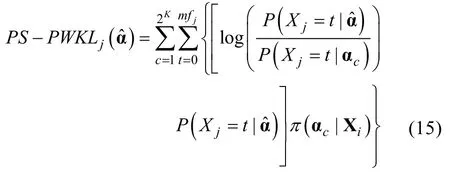
PS-HKL信息量是在PS-PWKL信息量的基础上进一步考虑了知识状态间的相似性, 若用表示知识状态间的相似性, 且:
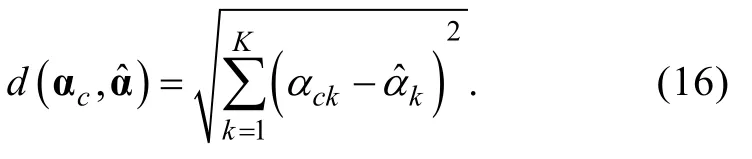
则PS-HKL信息量(Hybrid KL)可计算为,
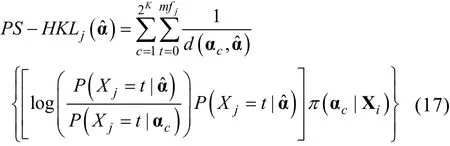
即在psCD-CAT下, 挑选对被试当前知识状态估计值ˆα具有最大信息量(如最大PS-KL, PS-PWKL或PS-HKL)的试题, 也即挑选测量/诊断误差最小的试题给被试作答。
2.4 多级评分的CD-CAT终止规则
CD-CAT的终止规则主要分两种:定长(fixed length)与不定长(variable length)。定长CD-CAT是指固定CD-CAT的测验长度(如15题), 即如果某被试在CD-CAT中达到了该长度, 则停止测试。定长CD-CAT的特点是所有被试所用的题量均相等; 不定长CAT是指固定测量精度, 即如果某被试在CD-CAT中达到某一设定的测量精度, 则停止测试。不定长CD-CAT的特点是被试的测量精度基本一致, 但被试所有的题量不尽相同。Hsu等(2013)以及Tatsuoka (2002)在其研究中曾使用后验概率(posterior probability)作为不定长CD-CAT的测量精度指标, 即当被试判为某个知识状态的后验概率达到事先要求水平(如0.85), 则终止测试, 本研究拟沿用这一做法。
3 Monte Carlo模拟研究
为了进一步验证研究第二部分关于多级评分的psCD-CAT设计的可行性, 本文采用Monte Carlo模拟实验方法进行, 具体如下:
3.1 题库结构及其Monte Carlo模拟
题库共测量6个独立的认知属性, 则共有26=64种被试掌握模式即知识状态和26– 1=63种项目测量模式。为了保证题库中各种类型的试题以及CDCAT中各种类型的被试都有, 本研究共模拟63×5=315道试题, 即各种项目测量模式均重复5次;同时, 模拟64×25=1600名被试, 即每种知识状态的被试重复25次试; 项目参数则从如下均匀分布中随机生成,sjt~U(0,0.6),gjt~U(0,0.6),并控制sjt<= s jt+1和gjt>= gjt+1具体控制的方法是:如果随机产生的s或g大于0.6则重新产生, 直至产生的值在(0, 0.6)区间; 对于同一题多个s和g参数, 则分别通过排序的方法, 以控制控制sjt<= s jt+1和gjt>= gjt+1。为便于说明问题, 本题库中所有试题均采用满分为3分的评分方式。
3.2 实验条件
3.2.1 多级评分的认知诊断模型
采用GP-DINA模型, 该模型在涂冬波等人(2010)提出的P-DINA模型拓展而来(详见本文2.1部分)。
3.2.2 参数估计方法
Hsu等(2013)以及Huebner和Wang (2011)的研究中将知识状态的先验概率P(αc)假定为均匀分布,即, 这时MAP与MLE等价。本研究采用Hsu等(2013)和Huebner和Wang (2011)的这一做法, 即参数估计采用MAP/MLE算法。
3.2.3 选题策略
将本研究2.3部分设计的PS-KL、PS-PWKL和PS-HKL三种选题策略运用到psCD-CAT中, 即选择具有相应最大信息的试题, 并与随机选题策略(记为Random)作为参照基准。
3.2.4 终止规则
定长和不定长CD-CAT两种。定长CD-CAT中固定测试长度为L题, 即每个被试测试L题(L=10,15, 20)结束测试; 不定长CD-CAT中采用固定测量精度, 固定后验概率为, 即测试中当被试判为某个知识状态的后验概率达到p时则终止测试。
3.3 评价指标
3.3.1 属性判准率(Classification Accuracy)
采用单个属性判准率(Attribute Match Ratio, AMR)和所有属性平均边际判准率(Average Attribute Match Ratio, AAMR)和模式判准率(Pattern Match Ration,PMR)三个评价指标。
3.3.2 题库安全性(Test Security)
采用题库整体曝光率(exposure rate)和测验重叠率(test overlap ration, TOR)指标来衡量题库的安全性。
题库整体曝光率(exposure rate)反应了题库题目整体的曝光程度, 也即反应了题库的安全性, 一般采用卡方类计算指标, 具体见公式18。

其中,ERj指第j题的曝光率,,fj指第j题被调用的次数,N为测试总人数,ERj越小说明该题的曝光率越低;为项目j期望曝光率, 在CD-CAT中, 理想情况是所有项目都被均匀调用, 即所有项目调用的期望次数或期望曝光率应该相等, 也就是(定长psCD-CAT中L为测验长度, 不定长G-D-CAT中L为平均测验长度;M为题库总题量)。因此公式18中, χ2统计量可以反应观察的曝光率与期望曝光率之间的差异, 因此χ2统计量越小说明题目调用的越均匀, 也即题库越安全。
测验重叠率(test overlap ration, TOR)是反应不同被试共同调用试题的重叠情况, 重叠率越高说明题库越不安全。因此测验重叠率的计算与项目曝光率、测验长度和被试量有关, Chen, Ankenmann和Spray (2003)在其研究中给出如下计算公式。

3.3.3 测验效率
测验效率(test efficiency)主要用来评价不定长psCD-CAT的测试效率, 即在相同测量精度下, 平均使用的题数即为测验效率。如果平均使用的题数越少说明psCD-CAT测试的效率越高, 反之效率越低。

指不定长CD-CAT中被试i使用的题数。
3.4 实验设计
实验1:定长条件下psCD-CAT效果。采用3×4两因素实验设计, 第一因素为测验长度, 分10、15和20题三个水平; 第二个因素为选题策略, 分随机选题策略、PS-KL、PS-PWKL和PS-HKL四种选题策略。
实验2:不定长条件下psCD-CAT效果。采用3×4两因素实验设计, 第一因素为测量精度指标——后验概率p, 分0.75、0.80和0.85三个水平; 第二个因素为选题策略, 分别为随机选题策略、PS-KL、PS-PWKL和PS-HKL四种选题策略。
4 研究结果
4.1 实验1定长条件下多级评分的psCD-CAT效果
表2和表3分别是定长psCD-CAT下的被试属性诊断正确率及题库安全性的结果。
表2说明, 不论在何种测验长度下(10, 15和20题),PS-PWKL和PS-HKL选题策略具有较高的诊断正确率, 且两种选题策略均优于PS-KL选题策略, 但随着测验长度的增加, 这种差异越来越小; 表2还说明在实验1设计下, 若要保证有90%以上属性模式诊断正确率(PMR), 则psCD-CAT的题长应在15题左右。表3表明与PS-KL相比, PS-PWKL和PS-HKL具有更低测验重叠率及题库曝光率, 因此题库使用更为安全, 而PS-PWKL和PS-HKL则具有相似的测验重叠率及题库安全性, 但与随机选题策略(Random)相比, PS-PWKL和PS-HKL选题策略在题库安全性上还有进一步提高的空间。
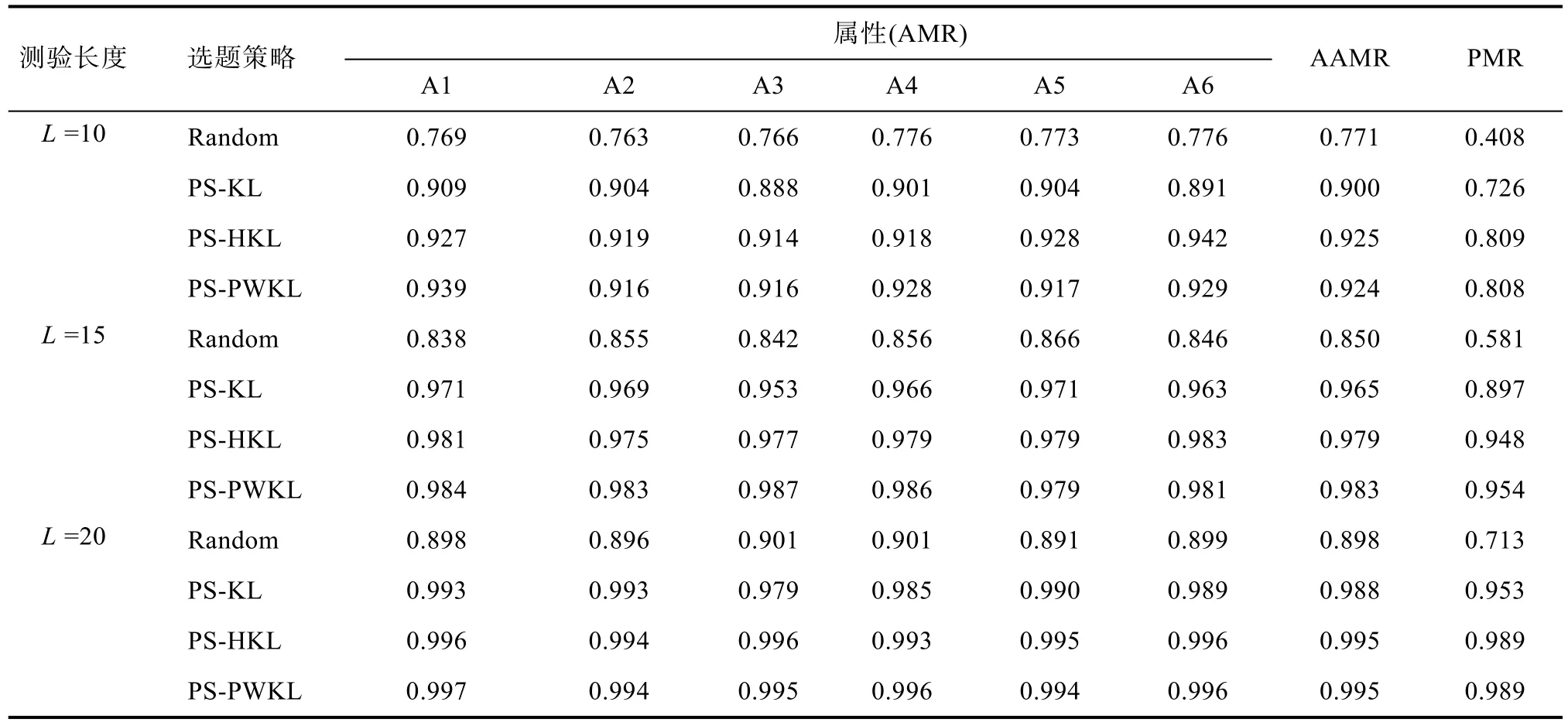
表2 定长psCD-CAT的诊断正确率

表3 定长psCD-CAT的题库安全性
总之, 实验1结果表明, 在PS-PWKL和PS-HKL选题策略下, 本研究设计的定长psCD-CAT具有较理想的属性判准率, 且题库的安全性尚可。几种选题策略相比较而言, PS-PWKL和PS-HKL选题策略整体上最佳, 而PS-KL选题策略相对差一些, 但随机选题策略因其非常低属性诊断正确率(尤其是PMR指标)而不太适用于psCD-CAT环境。
4.2 实验2:不定长条件下多级评分的psCDCAT效果
表4和表5分别是不定长psCD-CAT下的被试属性诊断正确率及题库的安全性与测验效率的结果。
表4和表5说明, 在固定测量精度条件下, 基于KL的3种选题策略属性诊断正确率间的差异不如定长psCD-CAT大, 且比较接近。但为了达到相近的诊断正确率, PS-KL平均使用(10.2+11.14+11.79)/3=11.04题, 而PS-PWKL和PS-HLK则分别使用了(8.48+8.83+9.15)/3=8.82题和(8.43+8.67+9.25)/3=8.78题, 因此测验效率指标上, PS-KL选题策略不如后两者; 同时表5还说明, PS-PWKL和PS-HLK比PS-KL具有更低的测验重叠率和题库曝光率, 因此题库使用显得相对更为安全。
学校立足艺术教育,必然要以特色课程作支撑。基于传承和发展本土嘉禾文化、岭南文化的背景,白云艺术中学大力建设“岭南艺术”特色课程,以音乐和美术系列为核心系列课程,兼设学科拓展系列和实践活动系列课程。特色课程让学生深入了解岭南艺术,促进学生对本土文化的认识和热爱,提升学生的艺术鉴赏力、分析力以及艺术素养,从而发展学生的艺术创作能力。

表4 不定长psCD-CAT的诊断正确率
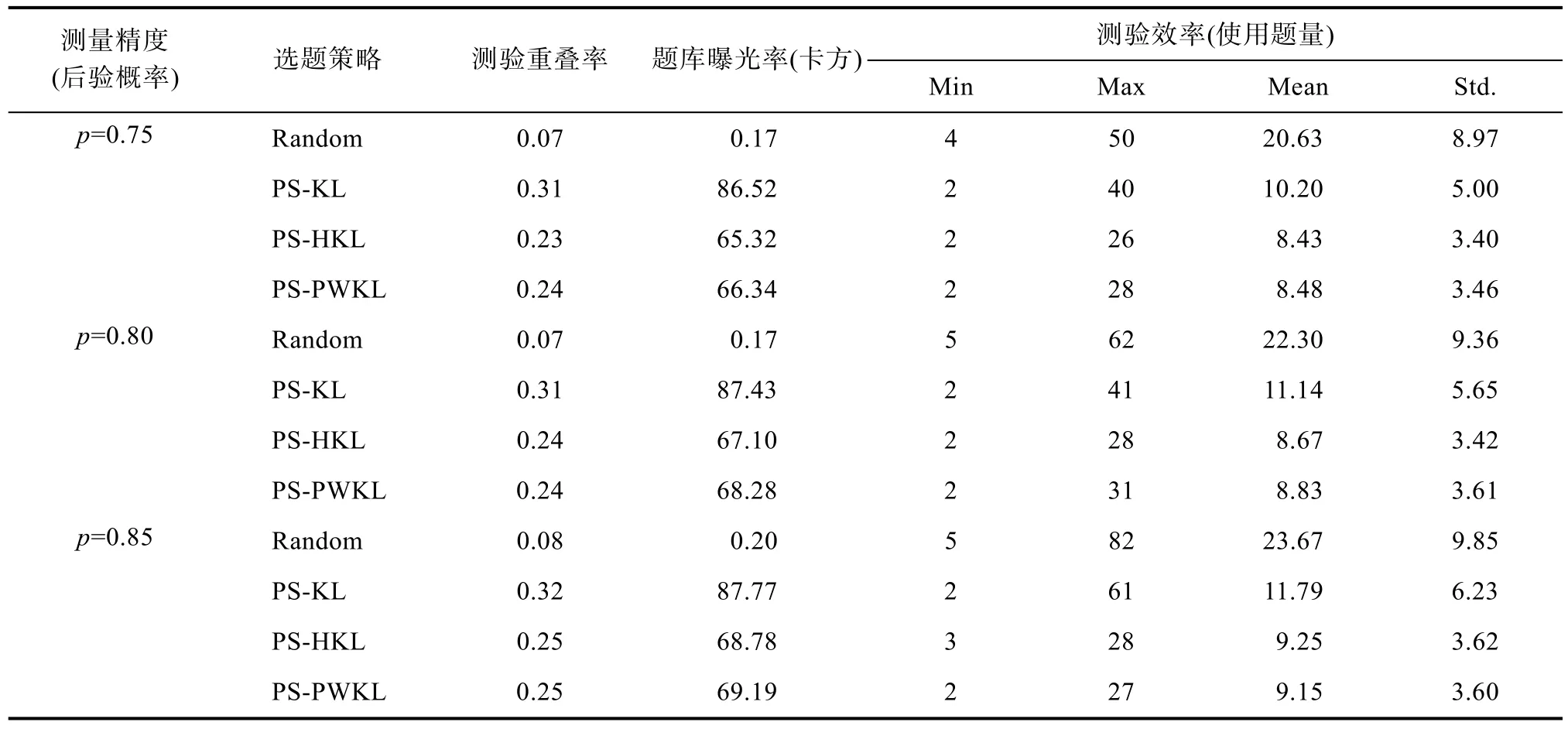
表5 不定长psCD-CAT的题库安全性与测验效率
总之, 实验2结果表明, 在PS-PWKL和PS-HKL选题策略下, 总体来讲本研究设计的不定长psCDCAT同样具有较高的KS判准率, 且题库的安全性较理想。几种选题策略相比较而言, PS-PWKL和PS-HKL选题策略整体上最佳, 具较高的测验效率及题库安全性。
5 讨论展望与研究结论
CD-CAT因充分结合了认知诊断和CAT两者的优势而深受国内外研究者和应用者的推崇。目前,国内外学者对CD-CAT也开展了大量的研究, 研究领域涉及选题策略、曝光控制、参数估计算法等领域研究。但比较可惜的是, 目前国内外针对CD-CAT的研究基本上仅针对二级评分数据展开,而针对多级评分数据的CD-CAT的还几乎未真正展开; 但在实际应用中, 多级评分数据大量存在,而这是传统0-1评分的CD-CAT显然无法满足实际的需求, 这不利于推动CD-CAT在实际中的应用与推广。因此, 针对多级评分的CD-CAT的研究则显得十分必要。本文抛砖引玉, 以期更多研究者从事这一领域研究, 从而为真正推动CD-CAT为实际服务而努力。
5.1 讨论与展望
5.1.1 多级评分CD-CAT与传统0-1评分CD-CAT比较
5.1.2 psCD-CAT项目自动评分研究
要真正实现多级评分CD-CAT, 则离不开项目在线自动评分, 否则自适应无法进行。因此多级评分项目的自动评分技术有待进一步跟进。比较可喜的是, 英语作文评分目前国际上已实现了计算机自动评分, 中文作文自动评分的技术也日益发展并不断成熟, 这些技术都为多级评分CD-CAT提供了重要的技术支持, 我们也深信随着人工智能技术以及测量技术的不断发展, 多级评分综合题的自动评分将会迎刃而解。
5.1.3 psCD-CAT下新选题策略的探讨
本研究将传统CD-CAT的KL, PWKL和HKL选题策略的思想方法应用于psCD-CAT环境中, 拓展出了PS-KL, PS-PWKL和PS-HKL三种适用于多级评分认知诊断计算机化适应测验的选题策略, 从而提供了新的方法技术, 但未来研究可以进一步考虑CD-CAT中香农熵(Xu, Chang, & Douglas, 2003)和互信息量(Mutual information, Wang, 2013)等选题策略在psCD-CAT中的效果, 并比较不同选题策略的特点及性能, 从而为实践者在选题策略的选用上提供进一步的指导。
5.1.4 psCD-CAT下曝光率控制技术
曝光率控制是CAT和CD-CAT领域中一项非常重要技术。过高的测验曝光率不仅会严重危害到测验的安全性, 更会使测验项目的性能发生改变(如参数漂移)从而影响到测量结果的精度。限于篇幅及精力, 本研究并没有深入探讨psCD-CAT环境下的题库安全性控制技术, 未来研究有待进一步展开, 以保证属性诊断正确率的前提下, 进一步提高题库使用的安全性。
5.1.5 psCD-CAT的应用研究
本文仅是通过Monte Carlo模拟的方法验证了psCD-CAT的效果与性能, 未来研究更需要实际中进一步验证psCD-CAT的效果。
5.2 研究结论
本研究在传统CD-CAT的基础上进行拓展, 开发设计了可以处理多级评分的CD-CAT (记为psCDCAT)。因此, 本文最大的特色/贡献在于开发多级评分的CDM, 并使真正用多级评分CDM来处理多级评分的CD-CAT。Monte Carlo模拟实验结果表明:在PS-PWKL和PS-HKL选题策略下, 基于多级评分框架下设计的psCD-CAT具有较好的诊断正确率、题库安全性和较高的测验效率, 说明本研究设计开发的psCD-CAT基本可行, 可以用于实现多级评分的计算化自适应诊断, 弥补了传统CD-CAT只能处理0-1评分数据的不足; Monte Carlo模拟实验还同时表明PS-PWKL和PS-HKL选题策略具有较理想的被试属性诊断正确率、题库安全性和高测验效率。总之, 本研究对于进一步拓展CD-CAT在实践中的应用提供了重要的方法和技术支持。
Chen, P., & Xin, T. (2011). Item replenishing in cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica, 43(7), 836−850.
[陈平, 辛涛. (2011). 认知诊断计算机化自适应测验中的项目增补.心理学报,43(7), 836−850.]
Chen, S. Y., Ankenmann, R. D., & Spray, J. A. (2003). The relationship between item exposure and test overlap in computerized adaptive testing. Journal ofEducational Measurement, 40, 129-145.
Chen, Y. X., Liu J. C., & Ying, Z. L. (2015). Online item calibration for Q-Matrix in CD-CAT.Applied Psychological Measurement,39(1), 5−15.
Cheng, Y. (2009). When cognitive diagnosis meets computerized adaptive testing: CD-CAT.Psychometrika, 74, 619–632.
Feng, Y., Habing, B., Huebner, A. (2014). Paramter estimation of the reduced RUM using the EM algorithm. Applied Psychological Measurement, 38(2), 137-150.
Guo, L., Zheng, C. J., & Bian, Y. F. (2015). Exposure control methods and termination rules in variable-length cognitive diagnostic computerized adaptive testing.Acta Psychologica Sinica, 47(1), 129−140.
[郭磊, 郑蝉金, 边玉芳. (2015). 变长CD-CAT中的曝光控制与终止规则.心理学报, 47(1), 129−140.]
Hsu, C. L., Wang W. C., & Chen, S. Y. (2013). Variable-length computerized adaptive testing based on cognitive diagnosis models.Applied Psychological Measurement, 37(7), 563−582.
Huebner, A., & Wang, C. (2011). A note on comparing examinee classification methods for cognitive diagnosis models.Educational and Psychological Measurement,71(2), 407−419.
Kaplan, M., de la Torre, J., & Barrada, J. R. (2015). New item selection methods for cognitive diagnosis computerized adaptive testing.Applied Psychological Measurement, 39(3),167−188.
Mao, X. Z., & Xin, T. (2013). The application of the Monte Carlo approach to cognitive diagnostic computerized adaptive testing with content constraints.Applied Psychological Measurement, 37(6), 482−496.
Samejima, F. (1995). Acceleration model in the heterogeneous case of the general graded response model.Psychomatrika,60, 549–572.
Samejima, F. (1997). Graded response model. In W. J. van der Linden & R. K. Hambleton (Eds.),Handbook of modern item response theory(pp. 85–100). New York: Springer.
Tatsuoka, C. (2002). Data analytic methods for latent partially ordered classification models.Journal of the Royal Statistical Society: Series C (Applied Statistics), 51, 337− 350.
Tu, D. B., & Cai, Y. (2015). The development of CD-CAT with polytomous attributes.Acta Psychologica Sinica, 47(11),1405−1414.
[涂冬波, 蔡艳. (2015). 基于属性多级化的认知诊断计算机化自适应测验设计与实现.心理学报, 47(11), 1405− 1414.]
Tu, D. B., Cai, Y., & Dai, H. Q. (2013). Item selection strategies and initial items selection methods of CD-CAT.Journal of Psychological Science, 36(2), 469−474.
[涂冬波, 蔡艳, 戴海琦. (2013). 认知诊断CAT选题策略及初始题选取方法.心理科学, 36(2), 469−474.]
Tu, D. B., Cai, Y., Dai, H. Q., & Ding, S. L. (2010). A polytomous cognitive diagnosis model: P-DINA model.Acta Psychologica Sinica, 42(10), 1011−1020.
[涂冬波, 蔡艳, 戴海崎, 丁树良. (2010). 一种多级评分的认知诊断模型: P-DINA模型的开发.心理学报, 36(4),1011–1020.]
Wang, C. (2013). Mutual information item selection method in cognitive diagnostic computerized adaptive testing with short test length.Educational and Psychological Measurement,73(6), 1017−1035.
Wang, C., Chang, H. H., & Huebner, A. (2011). Restrictive stochastic item selection methods in cognitive diagnostic computerized adaptive testing.Journal of Educational Measurement, 48, 255−273.
Wang, W. Y., Ding, S. L., & Song, L. H. (2014). Item selection methods for balancing test efficiency with item bank usage efficiency in CD-CAT.Journal of Psychological Science,37(1), 212−216.
[汪文义, 丁树良, 宋丽红. (2014). 兼顾测验效率和题库使用率的CD-CAT选题策略.心理科学, 37(1), 212−216.]
Xu, X. L., Chang, H. H., & Douglas, J. (2003, April). A simulation study to compare CAT strategies for cognitive diagnosis.Paper presented at the Annual Meeting of National Council on Measurement in Education, Montreal, Canada.
Zhou, J., Ding, S. L., & Chen, P. (2007). The method of cognitive diagnosis CAT based on polytomous scoring model.Journal of Jiangxi Normal University (Natural Science), 31(4), 375−378.
[周婕, 丁树良, 陈平. (2007). 多级评分CAT的认知诊断方法.江西师范大学学报(自然科学版), 31(4), 375−378.]
