基于平稳遍历函数型数据改良核回归估计渐近正态性

孙　婷,　凌能祥

(合肥工业大学 数学学院,安徽 合肥　230009)



基于平稳遍历函数型数据改良核回归估计渐近正态性

孙婷,凌能祥

(合肥工业大学 数学学院,安徽 合肥230009)

摘要:文章基于解释变量X具有函数特征而响应变量Y取值于实数空间R的条件下,研究了基于平稳遍历函数型数据改良核回归估计的渐近性质。利用经典的N-W核估计的方法构造了回归函数r(x)的改良核估计,在一定的条件下,应用鞅差中心极限定理建立了基于平稳遍历函数型数据改良核回归估计的渐近正态性,从而推广了现有文献中的相关结果。

关键词:改良核回归估计;函数型数据;遍历过程;鞅差中心极限定理;渐近正态性

0引言

众所周知,回归函数的估计及其性质的研究是非参数统计推断的重要问题之一,它的结果在通信、统计模式识别及计量经济学等领域得到了广泛的应用。非参数回归函数的核估计方法是非参数回归估计的核心,在有限维场合下,无论在独立或某种相依情形下,很多学者都对回归函数核估计渐近性质进行了研究,如文献[1-4]。由于回归函数的核估计在通常情况下要求随机变量Y具有l阶矩,其中l>1,而非参数回归函数改良核估计有效地降低了对响应变量Y矩的要求,因此对回归函数改良核估计量的性质研究也是很有必要的。文献[5]构造了非参数回归函数改良核估计量,并研究了在i.i.d.下非参数回归函数改良核估计的强相合性及收敛速度。

近年来函数型数据广泛应用于经济、金融、环境等领域,因此,函数型数据的统计推断特别是非参数回归函数统计分析受到很多学者的关注。函数型数据最大的特点是数据具有函数性特征,在对函数型数据进行分析时,将观测到的数据看作一个整体,而不是一串数字。文献[6]提出了函数型非参数回归算子的N-W核估计,并获得了非参数回归算子估计量的渐近性质;文献[7]建立了α-混合函数型数据非参数回归函数的渐近正态性;文献[8]研究了基于相依函数型数据的回归函数估计,并获得了估计量的几乎必然收敛速度;文献[9]基于α-混合相依函数型数据条件下建立了回归算子的改良核估计,并获得了估计量的几乎完全收敛性和收敛速率。另一方面,实际上很难验证一个非线性时间序列是否为α-混合[10],而验证时间序列数据遍历性则相对比较简单,因此,研究平稳遍历函数型数据非参数回归函数估计量的性质也很有必要。文献[11]利用经典的N-W核估计方法研究了平稳遍历函数型数据下回归算子估计量的渐近正态性;文献[12]进一步研究了平稳遍历函数型数据下回归算子估计量的强逐点收敛速度及其一致收敛速度；文献[13]利用鞅的方法，建立了平稳遍历函数型数据下条件分位数估计的相合性。

本文利用鞅的方法研究了基于平稳遍历函数型数据改良核回归估计的渐近正态性。

1模型和假设

设(X1,Y1),…，(Xn,Yn)为同分布于(X,Y)的平稳遍历序列,其中(X,Y)为E×R上的一对随机变量，且X为定义在具有半度量d(·,·)的抽象的无限维函数空间E上,Yi、Y取值于实值空间R。对∀x∈E,回归算子定义为:

r(x)=E(Y|X=x)。

回归算子r的N-W核估计[8]为:

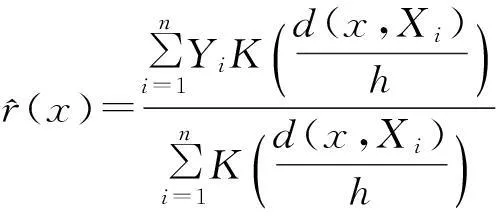
此时,进一步考虑回归函数的改良N-W核估计，即

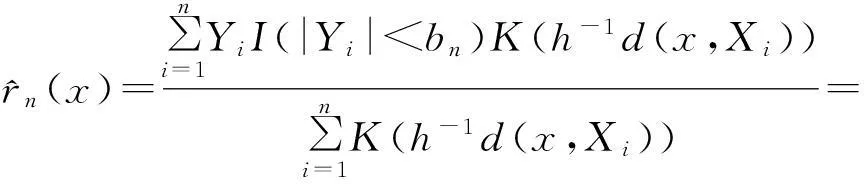
(1)

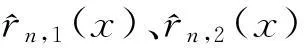
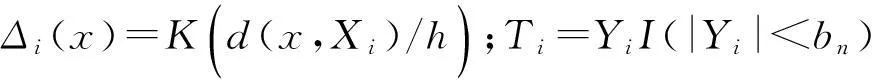
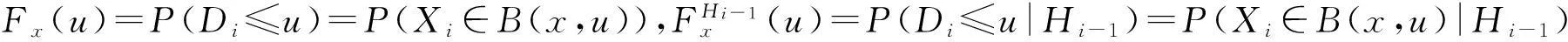
令

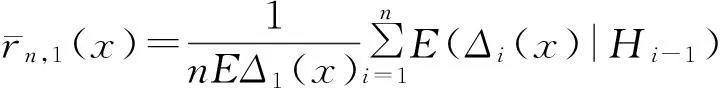
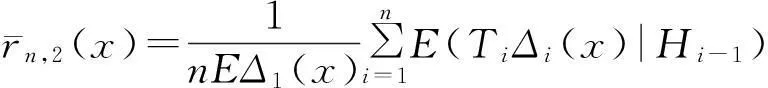
为了证明本文的主要结论,下面给出4个基本假设。

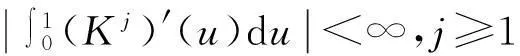
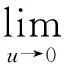
(1)Fx(u)=φ(u)f1(x)+o(φ(u)),u→0。

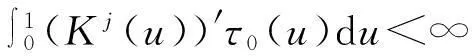
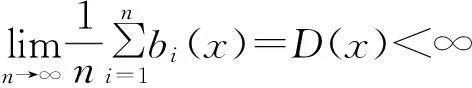
H3E[|Y2||X]≤C<∞。

H4该假设包含4个方面。

(1) 给定σ-域Gi-1,Yi的条件期望只取决于Xi,即E(Yi|Gi-1)=E(Yi|Xi)=r(Xi),对所有u,v∈E,存在β>0,c1>0,使|r(u)-r(v)|≤c1d(u,v)β。

(2) 给定σ-域Gi-1,Ti的条件期望只取决于Xi,即E(Ti|Gi-1)=E(Ti|Xi)=W1(Xi)。

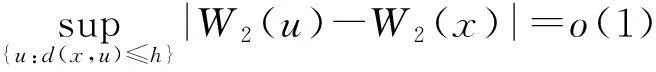
H1是研究函数型非参数回归函数估计量的常用假设,参见文献[8];H2表现了小球概率的性质,其在遍历性与函数型之间起重要作用,如文献[11-12];H3则在给定解释变量X下对响应变量Y做出条件矩的要求,其条件弱于文献[7]中相应的条件;H4体现了遍历性特征,对结论的证明起重要作用,详见文献[11]。

2主要结果

Bn(x)=Cn(x)-r(x)

(2)

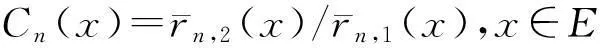
令Qn(x)和Rn(x)分别为:

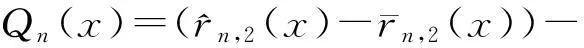
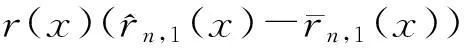
显然可得到:

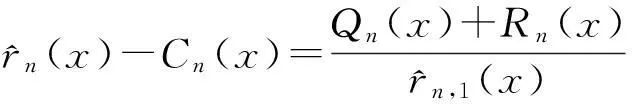
(3)

因此有:

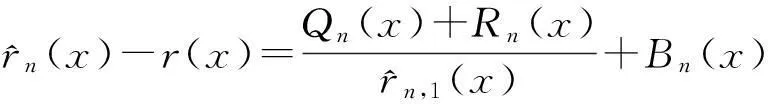
(4)

定理1假设H1～ H4成立,并且当n→∞时,满足以下条件:

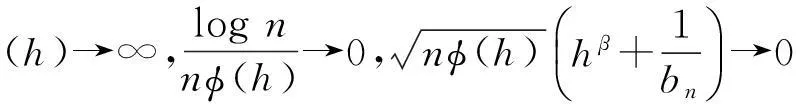
(5)

那么对于∀x∈E,使得f1(x)>0,则有:

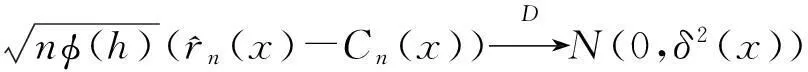
(6)

其中，对j≥1有：

再由(4)式、(5)式,则有:

(7)

3若干引理及定理的证明

3.1　基本引理及证明

引理1假设H1、H2(1)(2)(3)成立,且对任何实数1≤j≤2+δ,1≤k≤2+δ,δ>0,当n→∞时有:

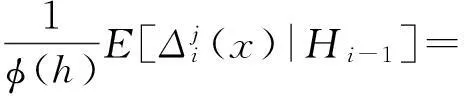
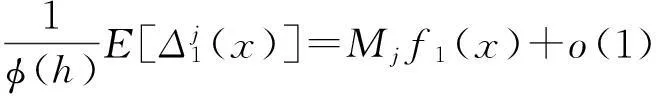
其中,

证明参见文献[11]引理1的证明。

引理2假设H1、H2成立且满足(5)式,对∀x∈E,则有:

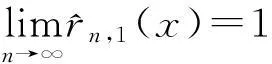
(8)

证明参见文献[12]引理3的证明。

引理3假设H1、H2、H3、H4(1)且(5)式成立,对∀x∈E,则有:

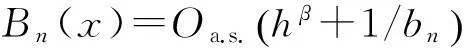
(9)

(10)

证明根据Bn(x)的定义,可直接得到:

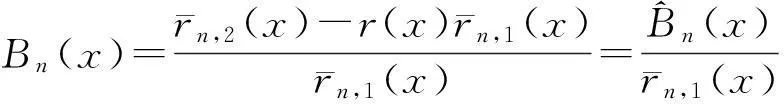
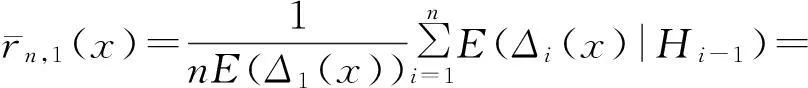
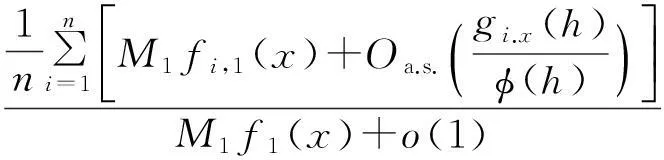
事实上,有

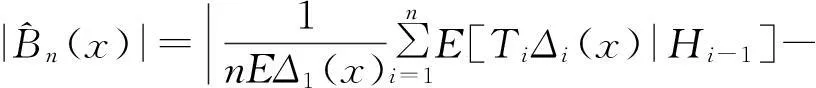
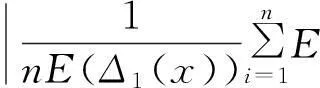
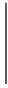
其中

E[TiΔi(x)-r(x)Δi(x)|Gi-1]=

E[TiΔi(x)-r(x)Δi(x)|Xi]=

E[YiΔi(x)-r(x)Δi(x)|Xi]-

E[YiI(|Yi|≥bn)Δi(x)|Xi]=

(r(Xi)-r(x))Δi(x)-Δi(x)E[YiI(|Yi|≥

Δi(x)E[YiI(|Yi|≥bn)|Xi]。

另外,可以得到:

E[YiI(|Yi|≥bn)|Xi]≤

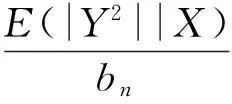
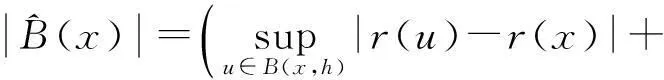
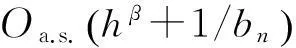
(9)式得证,另一方面,由文献[12]的(3.9)式有:

(11)

因此,结合(9)式、(11)式,可以证明(10)式成立。

引理4假设H1～H4成立,且满足(5)式,那么对于∀x∈E,使得f1(x)>0,则有:

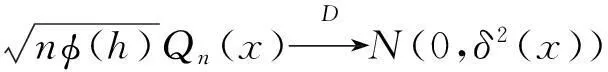
(12)

证明令

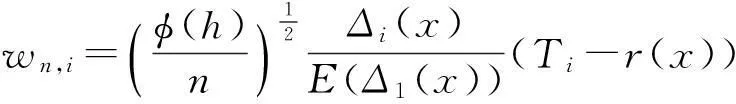
(13)

且定义vn,i=wn,i-E[wn,i|Hi-1],则可以得到:

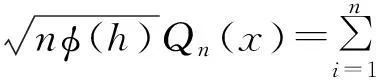
(14)

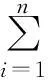
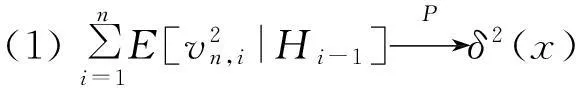
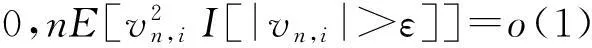
首先证明第1部分,显然可以得到如下不等式:

(15)

类似于引理3及利用引理1,则有：

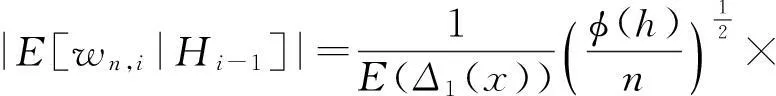
|E[(Ti-r(x))Δi(x)|Hi-1]|×

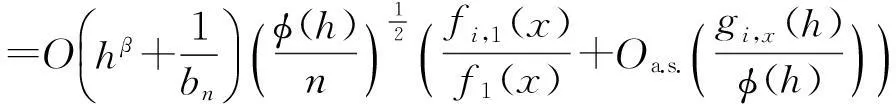
则只需证明(16)式成立,即可证明第1部分。

(16)

要证明(16)式,观察得到:

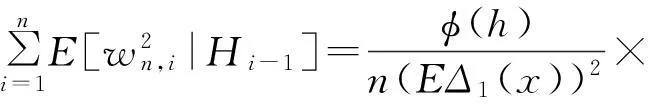
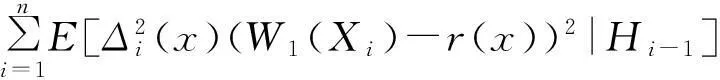
根据条件期望的性质,很容易得到:

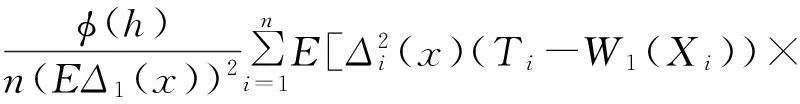
(W1(Xi)-r(x))|Hi-1]=0。

因此可直接得到:

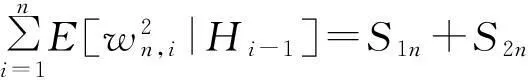
其中

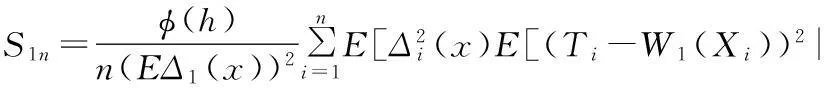
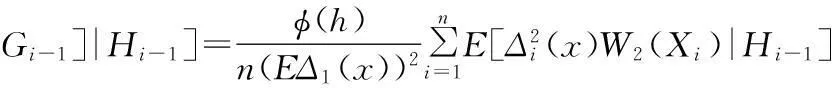
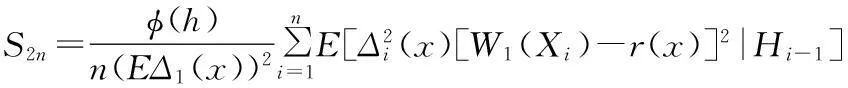
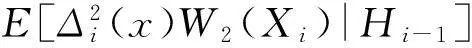
(17)

(18)

利用H4(3)可知:

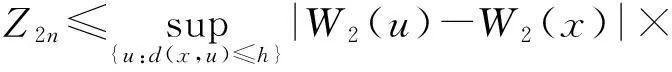
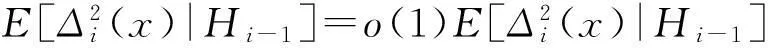
显然可以得到:

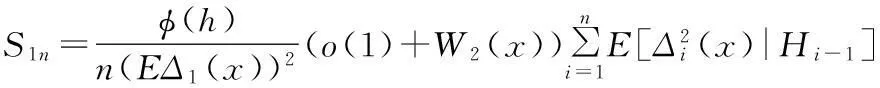
利用H2(2)(3)及引理1,可以得到:

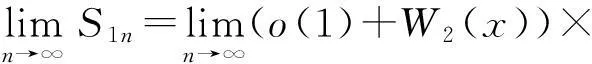
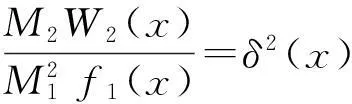
(19)

对于S2n,由W1(Xi)=E[Ti|Xi],则有:

r(x)-E(YiI(|Yi|≥bn)|Xi))2|Hi-1]|=

E(YiI(|Yi|≥bn)|Xi))2|Hi-1]|。

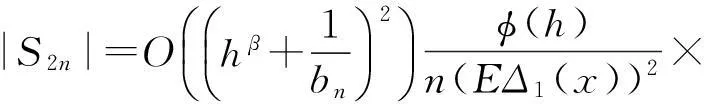
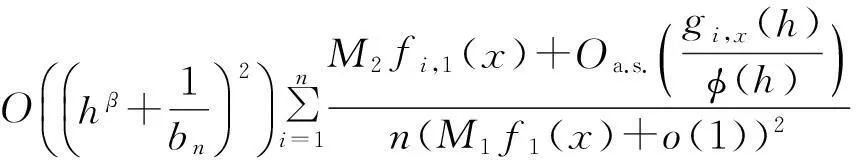
由引理1可知,|S2n|→0,a.s，因此可得:

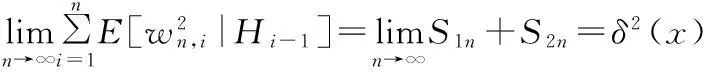
则第1部分得证。

3.2　定理1的证明

由(3)式和引理2、(10)式,结合引理4,即可证明(6)式,最后再结合(9)式则可证明(7)式,即定理1得证。

[参考文献]

[1]Devroye L.On the almost everywhere convergence of nonparametric regression function estimate[J].The Annals of Statistics,1981,9:1310-1319.

[2]Roussas G G,Nonparametric regression estimation under mixing conditions [J].Stochastic Processes and their Applications,1990,36:107-116.

[3]Roussas G G,Tran L T,Ioannides D A.Fixed design regression for time series:asymptotic normality [J].Journal of Multivariate Analysis,1992,40:262-291.

[4]Tran L T.Nonparametric function estimation for time series by local average estimators [J].The Annals of Statistics,1993,21:1040-1057.

[5]成平.回归函数改良核估计的强相合性及收敛速度[J].系统科学与数学,1983,3(4):304-315.

[6]Ferraty F,Vieu P.The functional nonparametric model and application to spectrometric data [J].Comput Stat,2002,17：545-564.

[7]Masry E.Nonparametric regression estimation for depedent functional data:asymptotic normality [J].Stochastic Processes and their Applications,2005,115:155-177.

[8]Ferraty F，Vieu P.Nonparametric functional data analysia[M].Theory and Practice.Berlin:Springer,2006:159-167.

[9]Ling N X,Wu Y.Consistency of modified kernel regression estimation for functional data [J].Statistics: A Journal of Theoretical and Applied Statistics,2012,2(46):149-158.

[10]范建青,姚琦伟.非线性时间序列:建模、预报及应用[M].陈敏,译.北京:高等教育出版社,2005:19-45.

[11]Laib N,Louani D.Nonparametric kernel regression estimation for functional stationary ergodic data:asymptotic properties[J]. Journal of Multivariate Analysis,2010, 101 (10):2266-2281.

[12]Laib N,Louani D.Rates of strong consistencies of the regression function estimator for functional stationary ergodic data[J].J Statist Plan Inference,2011,141(1) :359-372.

[13]魏亮瑜，凌能祥，李成好.基于遍历函数型数据条件分位数估计的相合性[J].合肥工业大学学报：自然科学版，2012，35(4)：557-562.

(责任编辑张镅)

Asymptotic normality of modified kernel regression

estimation for functional stationary ergodic data

SUN Ting,LING Neng-xiang

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

Abstract:In this paper, the asymptotic property of modified kernel regression estimation for functional stationary ergodic data is researched when the explanatory variable X has functional characteristic and the response variable Y is a scalar in real-value space R. Specifically, the modified kernel estimation of the regression function r(x) is constructed by using the classic Nadaraya-Watson estimator. Under certain conditions, the asymptotic normality of modified kernel regression estimation for functional stationary ergodic data is established by applying the martingale difference central limit theorem, which extends the α-mixing data to the functional stationary ergodic data.

Key words:modified kernel regression estimation; functional data; ergodic process; martingale difference central limit theorem; asymptotic normality

中图分类号:O212.7

文献标识码：A

文章编号：1003-5060(2015)11-1580-05