基于可变车道优化的交通网络设计问题

高　瑞,　龙建成

(合肥工业大学 交通运输工程学院,安徽 合肥　230009)



基于可变车道优化的交通网络设计问题

高瑞,龙建成

(合肥工业大学 交通运输工程学院,安徽 合肥230009)

摘要:针对“潮汐交通”问题所引起的道路资源利用不合理的现象,文章提出了考虑可变车道优化的交通网络设计问题,旨在通过合理的路段拓展和车道配置方案来提高交通网络的运行效率;构建了一个双层规划模型来描述提出的交通网络设计问题,上层问题以系统总阻抗与总投资额之和最小为目标,制定最优的道路拓展方案,并针对道路网络早晚高峰不同的OD需求水平,分时段对车道进行优化配置,下层模型采用了用户平衡(UE)配流模型来描述出行者在不同时段的路径选择行为;设计了人工蜂群算法来求解此双层规划模型。最后,采用数值算例验证了文中模型与算法的有效性。

关键词:交通网络设计;可变车道;双层规划;人工蜂群算法

0引言

近年来,随着国民经济的发展和城市化进程的不断加快,城市道路交通拥堵已成为影响城市居民生活质量的重要问题之一。要缓解城市交通拥堵问题,除了改、扩建道路外,还需要对道路资源进行优化分配[1]。为了更充分地利用有限的道路资源,尽可能地降低交通拥挤,很多国家和城市采用单行线和可变车道的办法来应对,取得了一定效果[2]。

通常城市道路以双向通行为主,2个车流方向的车道以中间为界,平均分配。然而,由于城市土地利用性质不同,易导致某些路段在早、晚高峰出现交通流量不均衡的现象。如早高峰时,郊区到中心城区的交通流量较大,同时中心城区到郊区交通流量相对较小。为了充分利用现有道路资源,可以考虑在高峰时段将交通流量大的路段实施交通管制,将更多的道路资源分配给交通流量较大的方向[3]。这种方法通过优化道路资源,可以缓解因“潮汐交通”而引起的道路交通拥堵。

一条双向交通流量不平衡的道路如图1所示,假设某一时段a到b方向的交通流量远远大于b到a方向的,则可以将b到a方向的1条或几条车道分配给a到b方向。特别地,当b到a方向车道全部分给a到b方向时,此时该路段变为a到b的单行道。类似地,也可以将a到b方向的车道分配给b到a方向。

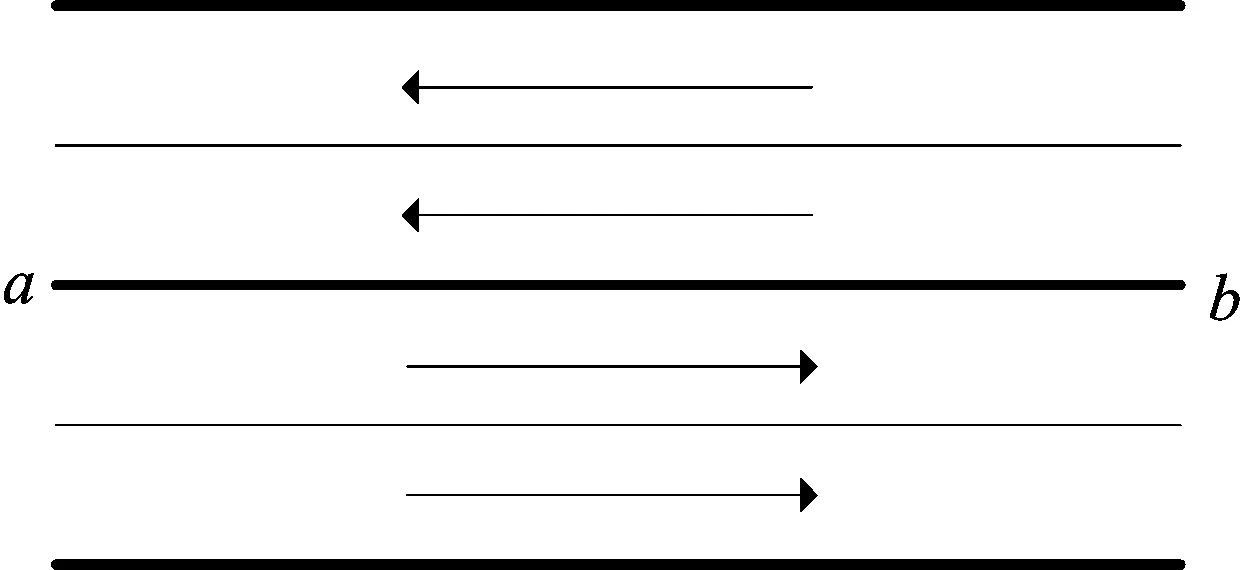
图1　双向道路示意图

目前,只有少数发达地区的城市应用了可变车道技术[4],而且仅限于部分拥挤严重的路段[5]。从效果上看,应用可变车道的个别路段交通拥挤情况有所改善,但是由于缺乏对整个路网出行费用合理的评估,可变车道的总体实施效果未知。

一般在城市中心区,道路网络已经规划成型,新建道路可能性极小,在原有道路基础上进行改、扩建相对而言较容易,如消除中央绿化带等方法。本文在离散网络设计问题[6-7]研究的基础上,针对“潮汐交通”引起的道路交通拥堵问题,不仅考虑对现有道路进行拓展(增加车道数),还考虑在不同的交通时段制定最优的可变车道实施方案。采用双层规划理论[8],以交通系统出行总费用最小为目标,建立考虑可变车道设置的城市道路网络设计的优化模型[9-10]。其中,上层问题为交通管理规划部门制定路段拓展方案,并优化各时段的车道分配方案;下层问题描述出行者基于用户平衡(UE)的路径选择行为。此外,可变车道的优化还考虑了不同时段交通需求的差异性。依据上层问题都是离散决策变量的模型特征,设计了人工蜂群算法对提出的双层规划模型进行求解。

1模型建立

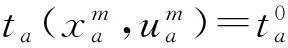
(1)

其中,α和β为模型参数,一般取α=0.15,β=4。

城市道路交通管理部门根据交通网络中高峰时段的交通需求情况,制定车道调整方案,以减小整个交通网络系统的阻抗,即系统总出行时间;出行者则根据道路车道设置情况调整个人出行,以期最小化个人出行成本。与大多数交通网络设计问题的相关文献[5]相同,本文假设出行者的路径选择遵循Wardrop用户平衡(UE)准则,采用UE配流模型来描述出行者的出行选择行为。

1.1　上层问题

交通管理部门在制定道路拓展方案以及可变车道设置方案时,需要同时考虑道路的拓展费用以及出行者的总出行费用,使得交通系统综合费用最小。因此,考虑可变车道的道路网络设计优化问题的上层问题可以描述如下:

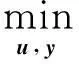
(2)

其中,Ga(ya)为道路拓宽的投资函数;u和y分别为路段分配的车道数和拓展车道构成的向量；x为路段流量构成的向量；φ为投资费用与出行时间的转换系数。

车道数守恒约束为：

(3)

非负和整数约束分别为：

(4)

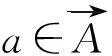
(5)

1.2　下层问题

本文采用UE配流模型来描述下层问题,即每个时段,网络流量达到平衡状态时,所有被利用的路径具有相等而且最短的走行时间,而未被利用的路径与其相比具有相等或更长的走行时间。对任意时段m,采用如下UE配流模型来得到平衡条件下的路段交通流量，即

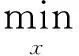
(6)

任意OD间各条路径上的交通量之和,应等于OD交通需求总量,即

(7)

路段流量与路径流量之间的关系描述为：

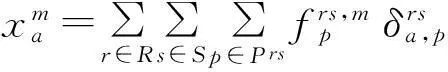
(8)

流量非负约束为：

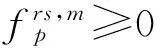
(9)

2求解算法

双层规划模型属于NP-Hard问题,传统的下降算法通常需要计算上层目标函数的导数,对于大规模问题这是非常困难的[8]。此外,下降算法往往只能得到局部最优解。智能优化算法是求解双层规划的有效方法之一[9]。

本文依据上层模型为离散决策变量的特征,设计了人工蜂群算法求解提出的双层规划模型。相比于传统遗传算法,人工蜂群算法具有非常好的局部搜索能力[11]。

人工蜂群算法[11-14]是模仿蜜蜂行为的一种优化方法，它通过对解集进行随机而有目标的操作寻求最优解。

2.1　解的编码和初始解的生成

图2　解的编码示意图

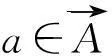
2.2　邻域操作

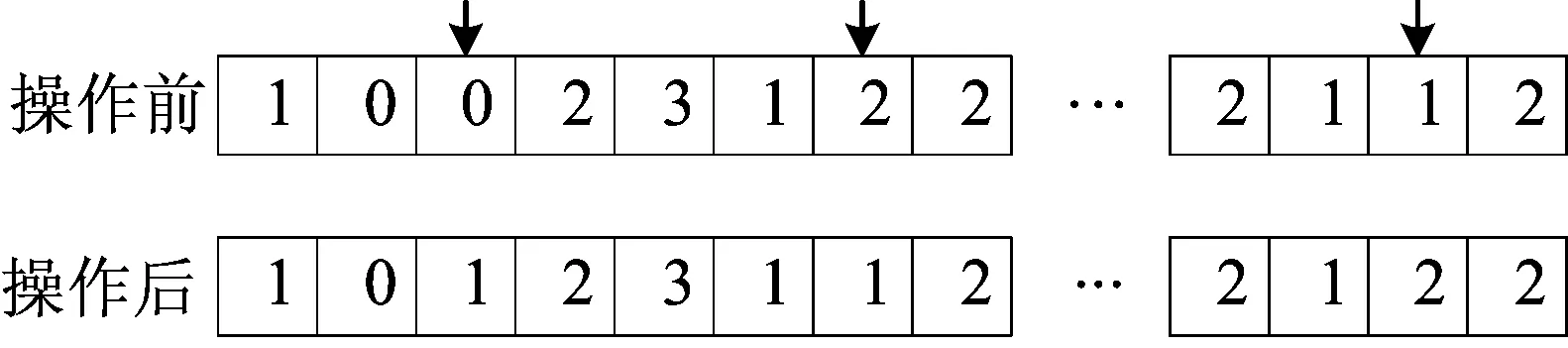
图3　点变异邻域操作示意图

2.3　适应度评价

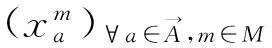
2.4　食物源选择

常用的食物源选择方法主要有轮盘赌选择法和锦标赛选择法[14]。本文选择轮盘赌选择法对食物源进行选择。

2.5　求解步骤

应用蜂群算法求解本文模型的步骤如下:

(1) 初始化。随机生成n个初始解{xi}(i=1,2,3，…,n),置迭代次数v=0和邻域搜索计数li=0(i=1,2,3,…,n);设置算法参数limit和MaxIterations。

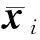
(5) 收敛判断。如果v=MaxIterations,算法结束;否则置v=v+1,返回步骤(2)。

3数值算例

本文采用图4所示的算例网络来验证所提出的模型与算法的有效性。该网络由9个节点、24条路段,72个OD对构成。算例网络路段参数见表1所列。早高峰时段的OD需求矩阵见表2所列。晚高峰时段的OD需求矩阵为早高峰OD需求矩阵的转置。

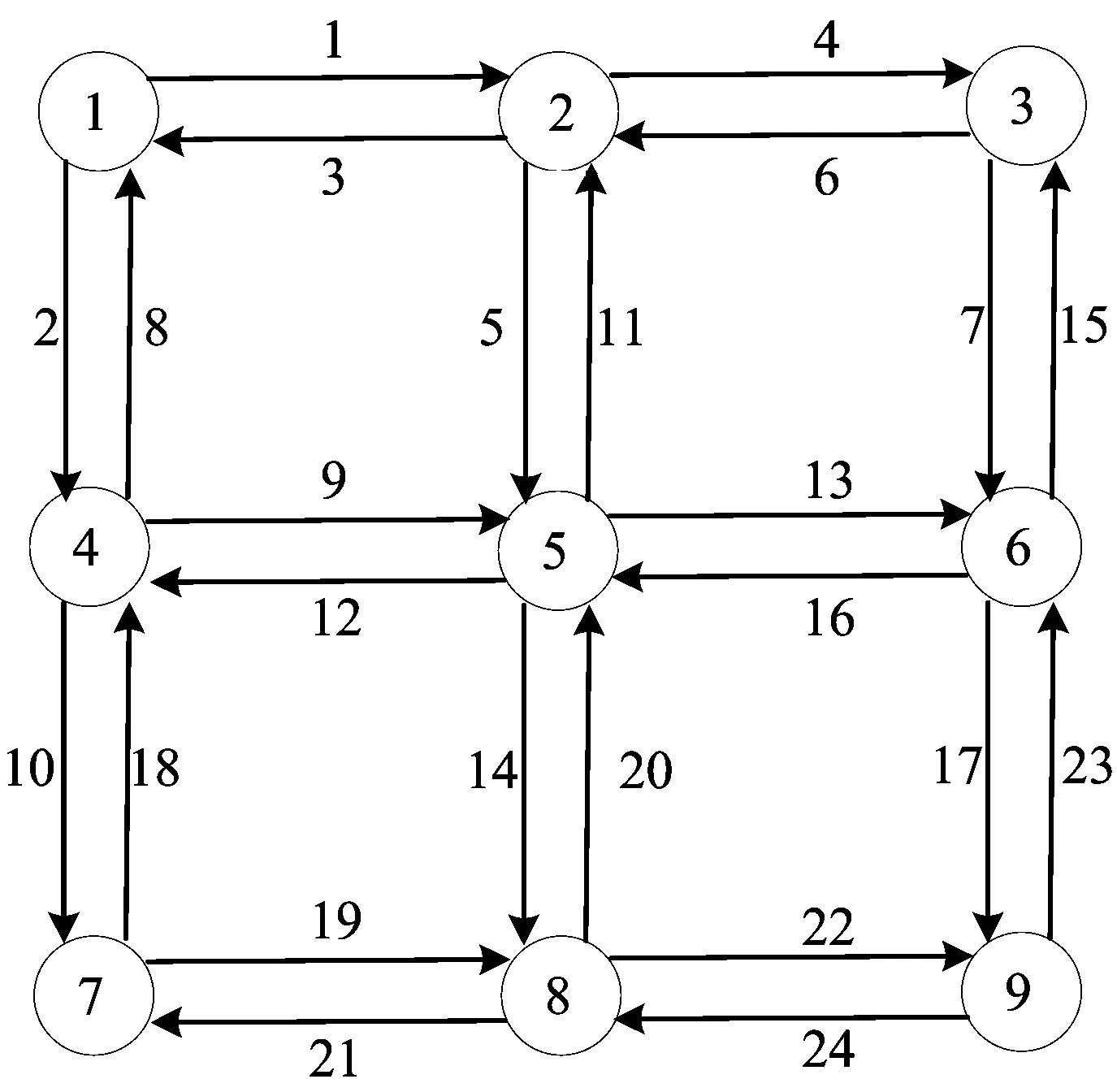
图4　算例网络示意图

表1　算例网络路段参数

表2　早高峰OD需求矩阵

路网未优化前，对早、晚高峰OD需求矩阵采用用户平衡(UE)配流方法进行流量分配，得到早、晚高峰系统总阻抗之和为2.45 h。运用本文方法，根据早、晚高峰OD需求矩阵对道路网络进行优化，得出车道优化配置方案。优化后，早晚高峰系统总阻抗之和降为2.28 h，比优化前降低了6.94%。其中，出行者总的出行成本为2.25 h，投资总额转化为出行费用部分为0.03 h。可见，提出的可变车道网络设计优化方案可以有效地降低系统总阻抗，实现现有资源和资金的合理利用。

表3　网络设计和可变车道优化结果

在人工蜂群算法和遗传算法的求解过程中,计算时间主要消耗在求解下层UE配流问题的求解上。因此,本文以下层UE配流问题的求解次数来评价不同算法的求解效率。

人工蜂群算法和遗传算法[16]都设置初始解的规模为10,UE配流次数为1 500次。遗传算法中交叉概率pm=0.8,变异概率pc=0.1。2种算法交通分配次数与目标函数值的关系如图5所示。由图5可知,人工蜂群算法计算到1 000次时已经得到最优目标函数值;而遗传算法计算1 400次才得出最优目标函数值。结果表明,在相同的计算时间内,人工蜂群算法得出的目标函数最优值要优于遗传算法的结果,即人工蜂群算法的求解效率优于遗传算法。

图5　用户平衡配流次数与最优目标函数值关系

4结束语

本文采用了双层规划模型来描述城市道路网络高峰时路段双向流量不平衡的网络设计问题,并考虑了可变车道的优化配置。其中,下层问题描述为一个多时段的用户平衡配流模型,上层问题描述为一个以系统总阻抗与总投资额之和最小为目标的整数规划问题。提出了人工蜂群算法来求解双层规划模型,得到最优的道路拓展方案和不同时段可变车道的配置方案。数值结果表明,本文提出的方法能有效地提高道路网络的利用率,降低道路交通拥挤。

本文提出的模型与算法为城市道路的建设和可变车道的调整提供了优化方案,并对拟提出的优化方案做出合理评价,最终实现交通规划与管理的统筹优化。本文的研究没有考虑可变车道设置对交叉口交通组织的影响,引入动态交通分配模型可以潜在地解决该问题,这将是进一步研究的方向。

[参考文献]

[1]张好智, 高自友.可变车道的道路交通网络设计优化方法[J].中国管理科学,2007,15(2):86-91.

[2]李丽丽,曲昭伟.可变车道的控制方法[J].吉林大学学报:工学版,2009,39(Z1):98-103.

[3]孙刚,王丰元.可变车道技术对提高交通高峰时段交通流量的研究[J].科技资讯,2006(25):176-177.

[4]崔妍,刘东.北京市朝阳路可变车道交通组织研究[J].道路交通与安全,2006,6(9):21-24.

[5]陈坚,霍娅敏.典型潮汐车流路段可变车道设置方案研究[J].重庆交通大学学报:自然科学版,2008,27(6):1127-1130.

[6]Gao Z Y,Wu J J,Sun H J.Solution algorithm for the bi-level discrete network design problem[J].Transportation Research Part B:Methodological,2005,39(6):479-495.

[7]Miandoabchi E,Daneshzand F,Szeto W Y,et al.Multi-objective discrete urban road network design[J].Computers and Operations Research,2013,40(10):2429-2449.

[8]高自友,宋一凡.城市交通连续平衡网络设计理论与方法[M].北京:中国铁道出版社,2000:89-91.

[9]高自友,张好智,孙会君.城市交通网络设计问题中双层规划模型、方法及应用[J].交通运输系统工程与信息,2004,4(1):35-44.

[10]Yang H,Bell M G H.Models and algorithms for road network design:a review and some new developments[J].Transport Reviews,1998,18(3):257-278.

[11]Karaboga D.An idea based on honey bee swarm for numerical optimization,Technical Report-TR06[R].Erciyes University,Engineering Faculty,Computer Engineering Department,2005.

[12]Singh A.An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem[J].Applied Soft Computing,2009,9(2):625-631.

[13]Szeto W Y,Jiang Y.Hybrid artificial bee colony algorithm for transit network design[J].Transportation Research Record Journal of the Transportation Research Board,2012,2284:47-56.

[14]Long J C,Szeto W Y,Huang H J.A bi-objective turning restriction design problem in urban road networks [J].European Journal of Operational Research,2014,237(2):426-439.

[15]Sheffi Y.Urban transportation networks:equilibrium analysis with mathematical programming methods[M].New Jersey:Prentice Hall,1985:111-132.

[16]周和平.基于遗传算法的公路网络设计的双层优化模型[J].同济大学学报:自然科学版,2005,33(7):920-925.

(责任编辑胡亚敏)

王保华(1972-),男,河南南阳人,博士，湖北汽车工业学院教授,硕士生导师.

A transportation network design problem with optimization of variable lanes

GAO Rui,LONG Jian-cheng

(School of Transportation Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:Unreasonable utilization of road resources can be arisen due to tidal traffic. To overcome this problem, a transportation network design problem(NDP) with consideration of optimization of variable lanes is proposed. The proposed NDP aims to improve traffic efficiency by designing reasonable road network and lane allocation. A bi-level programming model is developed to formulate the proposed NDP. The upper level problem aims to minimize the sum of the total system travel cost and the total investment by optimizing road expanding scheme. With consideration of the different OD demand levels in the morning and evening peak hours, the lane allocation schemes in different traffic demand periods are also optimized. The lower level problem is formulated as a user equilibrium(UE) traffic assignment model to describe travelers’ route choice behavior during different traffic demand periods. An artificial bee colony(ABC) algorithm is introduced to solve the proposed bi-level model. Finally, a numerical example is developed to illustrate the effectiveness of the proposed model and algorithm.

Key words:transportation network design; variable lane; bi-level programming; artificial bee colony(ABC) algorithm

doi:10.3969/j.issn.1003-5060.2015.11.003

作者简介：邓召文(1979-),男,山东安丘人,湖北汽车工业学院讲师;

基金项目：国家自然科学基金资助项目(51375151)；湖北省自然科学基金重点资助项目(2013CFA134)和湖北省重点实验室资助项目(ZDK1201504)

收稿日期：2014-10-06；修回日期：2015-03-04

中图分类号:U121

文献标识码：A

文章编号：1003-5060(2015)11-1446-05