基于Dijkstra拓展算法路线优化
2016-01-29杨丽娟刘渤海
杨丽娟, 刘渤海
(1.安徽工商职业学院 工商管理系, 安徽 合肥 231131; 2.合肥工业大学 管理学院, 安徽 合肥 230009)
基于Dijkstra拓展算法路线优化
杨丽娟1,刘渤海2*
(1.安徽工商职业学院 工商管理系, 安徽 合肥231131; 2.合肥工业大学 管理学院, 安徽 合肥230009)
摘要:利用Dijkstra算法,将配送中心的3个业务目标(距离、时间和费用)进行整合,建立可实现多目标的模型。对多目标Dijkstra算法进行了拓展,即一个配送中心对应两个客户配送以及车辆调度。
关键词:配送中心; 多目标; 车辆调度; 路线优化
0引言
0.1 相关背景
物流配送是物流中一个重要的直接与消费者相连的环节,配送的速度及质量直接关系到配送中心的工作质量和效益。随着经济的发展,物流配送中心的货运量逐渐增大,货物规格不断增多,需求运输车辆也逐渐增加,同时随着油价不断上涨,人工成本增加,使得配送中心的成本逐步增加。因此,对制定车辆配载计划和配送路线的优化就显得十分重要[1]。如何高效地制定出一个合理的车辆调度和路线优化方案,强化管理,降低成本,提高提润率,成为物流配送研究中一个亟待解决的问题[2]。
0.2 国内研究现状
目前国内配送中心在配送路线优化中,往往只为了实现单一目标,即距离、时间或是总费用,这导致配送中心在实际的作业过程中只单纯地追求最短路径、配送的最短时间或是配送的总费用[3]。而现实是最短的路径可能路况不好,或是最短的时间路况不好,过路费较高等,这都会造成配送成本不一定最低。与此同时,配送中心配送运输过程中产生的一些费用,如过路过桥费、车辆折旧费、管理费用、财务费用、信息费、驾驶员工资等。
文中在对配送中心的车辆路线设计相关理论研究中发现,主要分为单一目标和多目标(两个及以上)两大类型[4]。单一目标主要分为最短路径、最低费用和最短时间3种。具体方法如下:
1)单一目标----最短路径法。用于解决最短路径问题的算法被称做“最短路径算法”, 有时被简称作“路径算法”。 最常用的路径算法有:VSP规划法、Dijkstra算法、A*算法、SPFA算法、Bellman-Ford算法、Floyd-Warshall算法和Johnson算法。
2)单一目标----最低费用。具体运用到的方法主要有:遗传算法、分支切割算法、禁忌算法、模拟退火算法等,均属于较专业、较复杂的数学方法。
3)单一目标----最短时间。目前国内关于最短时间这一单一目标的研究较少,Dijkstra算法可以实现。
4)多目标----最短路径、最短时间、最低费用。
文中在调研时发现配送中心在运用数学方法实现多目标的研究较少,更多的专家集中在构建不同的数学模型实现单一的目标。
1关于配送中心车辆路线优化的研究
1.1 多目标Dijkstra算法的原理
针对物流配送中心如何根据货物运单来调度运输车辆的问题,在研究了各种货物配装优化模型的基础上,建立了车辆安排的多目标优化模型。然后,利用线性加权法和主要目标法将多目标优化问题转化为单目标优化问题,采用精确算法思想进行模型求解[5]。文中的多目标Dijkstra算法的情境是:单车场单送货车辆路径,未考虑路况、天气因素、发车时间限制、客户时间窗约束等情况下的车辆路径优化方法。
1.2 多目标Dijkstra算法具体方法
1.2.1权值的赋予
在这里权值主要分为3种:两点间距离、运行时间和费用。
距离权值比较容易确定,可以通过查阅《中国公路地图》或者到中国公路网等国内权威网站确定最短路径。
运行时间权值文中按照百度地图运行时间进行计算,也可以利用两点之间的距离和限速的最大值比较得来,即运行时间=路径/限速最大值。
费用主要包括:燃油费、过路过桥费、车辆折旧费、管理费用、财务费用、信息费、驾驶员工资等[6]。
1.2.2权重的赋值
对于距离、运行时间和费用3个指标权重的赋值是由配送中心根据自己的实际情况来确定。配送中心可以只考虑单一目标,也可以考虑2个目标,或者综合考虑3个目标[7]。
1.2.3运用多目标Dijkstra算法对配送中心车辆路线优化的研究
南京某配送中心有一批3.8 t的货物将从南京配送中心运至淮南客户(1.8 t)和蚌埠客户(2 t)处。所涉及的城市信息如图1所示。

图1 城市网络图
图中:线段上的数字为两点之间的距离(km),括号内的数字为运行时间(min),城市间的距离为两点直达路径距离,一部分是高速,另一部分是国道。
此配送中心可调度的车型有两种:2 t车和4 t车。具体信息如下:
配送中心共有两种车型可供选择:A型车,车自重1 t,核定载重2 t,数量5辆,空车油耗为4 L/(100 km),半载油耗7 L/(100 km),满载油耗10 L/(100 km);B型车,车自重2 t,核定载重4 t,数量4辆;空车油耗为6 L/(100 km),半载油耗10 L/(100 km),满载油耗18 L/(100 km)[8]。
此次业务中车辆调度方案有两辆2 t车分别配送和一辆4 t车共同配送,我们分别进行线路设计。
1.2.3.1方案1(调度两辆A型车分别配送)
第一辆2 t车从南京出发到蚌埠;第二辆2 t车从南京出发到淮南。
步骤1:费用核算。2 t货车油耗为10 L/(100 km),柴油价按照7.3元/L计算;过路费按照实际收费标准计算,安徽省高速公路10 t及以下的货车的计重收费标准为0.08元/(t·km)。车货总质量不足5 t按5 t计费;计重收费不足20元时,按20元计费。安徽省普通公路:根据实际车货总质量,小于10 t的车辆按2元/t车次计费[9]。各城市间的总费用见表1。
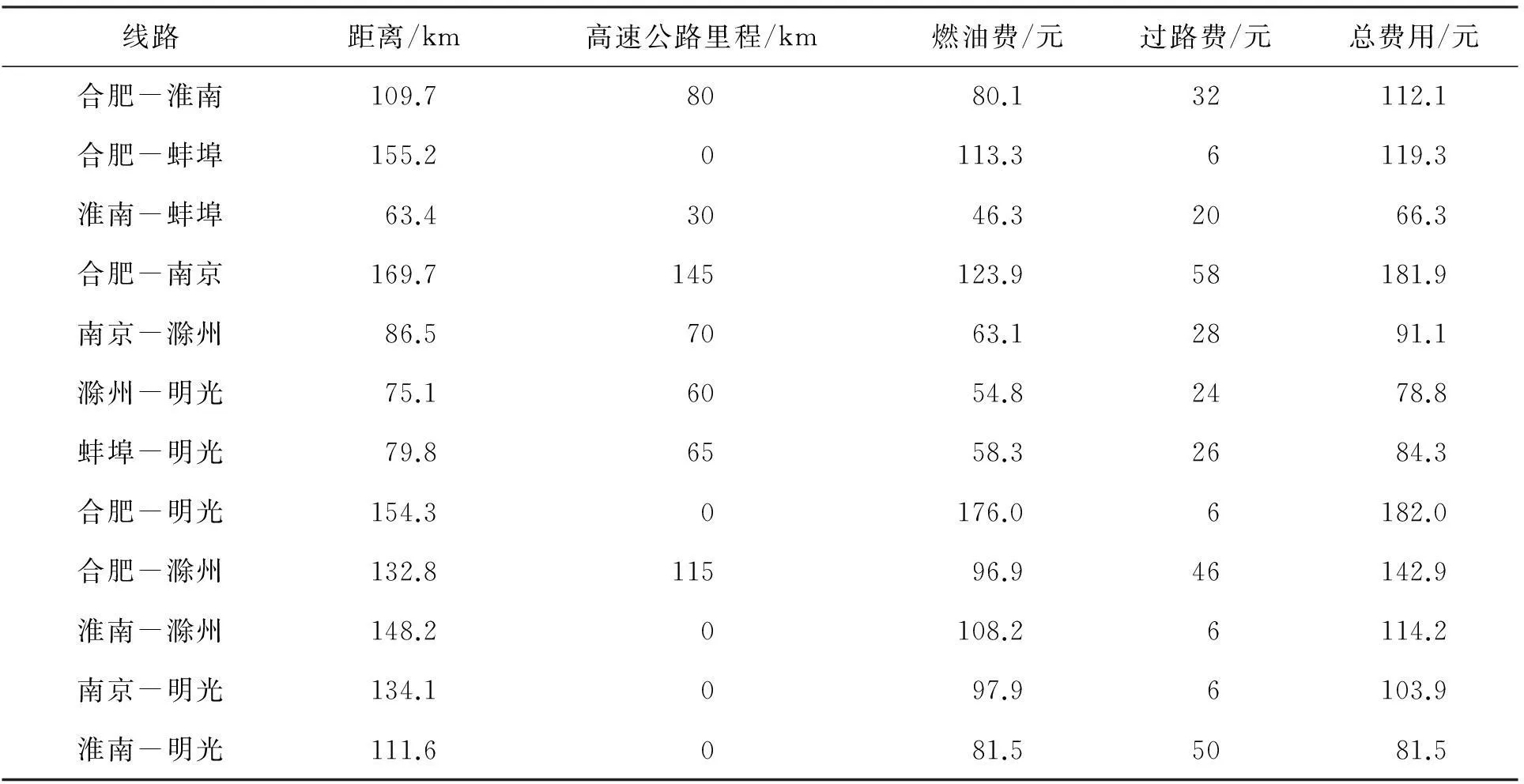
表1 城市间相关费用表
步骤2:城市间距离、时间、费用权值信息表。配送中心赋予距离、时间和费用的权重为0.3,0.3,0.4,根据权重和各指标的数值利用加权法计算得到3个指标的权值,具体信息见表2。
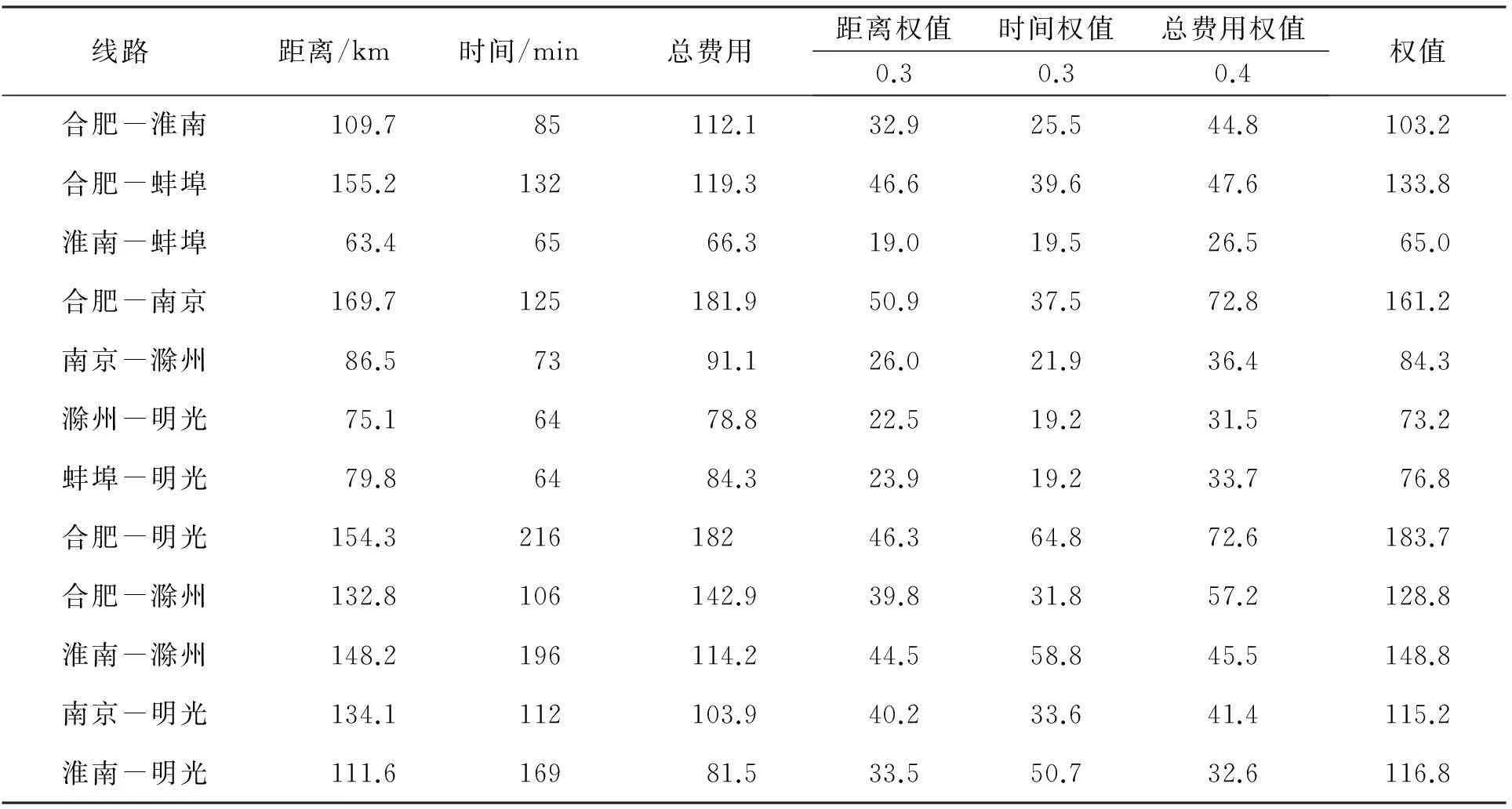
表2 城市间距离、时间、费用权值信息表
步骤3:第一辆2 t车“南京-蚌埠”线路权重计算。根据以上权值,利用多目标Dijkstra算法进行计算:
1)南京为已知解。与南京相连的有合肥、滁州、明光;南京-合肥权值为161.2,南京-滁州权值为84.3;南京-明光权值为115.2。所以取南京-滁州,滁州为已知解。
2)与南京和滁州相连的有合肥、淮南、明光。滁州-合肥总权值为213.1;滁州-淮南总权值为233.1;滁州-明光总权值为157.6;南京-合肥总权值为161.2;南京-明光权值为115.2。所以取最小值115.2,即路线南京-明光,明光为已知解。
3)与南京、滁州、明光相连的有合肥、淮南、蚌埠。南京-合肥总权值为161.2;滁州-淮南总权值为233.1;滁州-合肥总权值为213.1;明光-淮南总权值为232;明光-蚌埠总权值为192。所以取最小值161.2,即线路南京-合肥,合肥为已知解。
4)与南京、滁州、明光、合肥相连的有淮南、蚌埠。合肥-淮南总权值为264.5;合肥-蚌埠总权值为295;滁州-淮南总权值为233.1;明光-淮南总权值为232;明光-蚌埠总权值为192。所以取最小值192,即线路明光-蚌埠,蚌埠为已知解。
综上所述,此次配送的线路最终为:南京-明光-蚌埠,总权值为192。
步骤4:第二辆2 t车权值“南京-淮南”线路权重计算。我们利用多目标Dijkstra算法进行计算:
1)南京为已知解。与南京相连的有合肥、滁州、明光;南京-合肥权值为161.2,南京-滁州权值为84.3;南京-明光权值为115.2。所以取南京-滁州,滁州为已知解。
2)与南京和滁州相连的有合肥、淮南、明光。滁州-合肥总权值为213.1;滁州-淮南总权值为233.1;滁州-明光总权值为157.6;南京-合肥总权值为161.2;南京-明光权值为115.2。所以取最小值115.2,即路线南京-明光,明光为已知解。
3)与南京、滁州、明光相连的有合肥、淮南。南京-合肥总权值为161.2;滁州-淮南总权值为233.1;滁州-合肥总权值为213.1;明光-淮南总权值为232。所以取最小值161.2,即线路南京-合肥,合肥为已知解。
4)与南京、滁州、明光、合肥相连的有淮南。合肥-淮南总权值为264.5;滁州-淮南总权值为233.1;明光-淮南总权值为232。所以取最小值232,即线路明光-淮南,淮南为已知解。
第二辆2 t车配送的线路为:南京-明光-淮南,权值为264.5。综上所述,两辆2 t车的总权值为192+264.5=456.5。
1.2.3.2方案2(调度1辆4 t车进行路线优化设计)
步骤1:“南京-淮南段”总费用权值计算。因为车型不同,油耗不同,核定载重及自重不同,所以燃油费、过路费要重新计算。4 t车的前段路程满载状态油耗为18 L/(100 km)。

表3 城市间相关费用表
步骤2:南京-淮南段城市间距离、时间、费用权值信息表。配送中心赋予距离、时间和费用的权重为0.3,0.3,0.4,根据权重和各指标的数值利用加权法计算得到3个指标的权值,具体信息见表4。
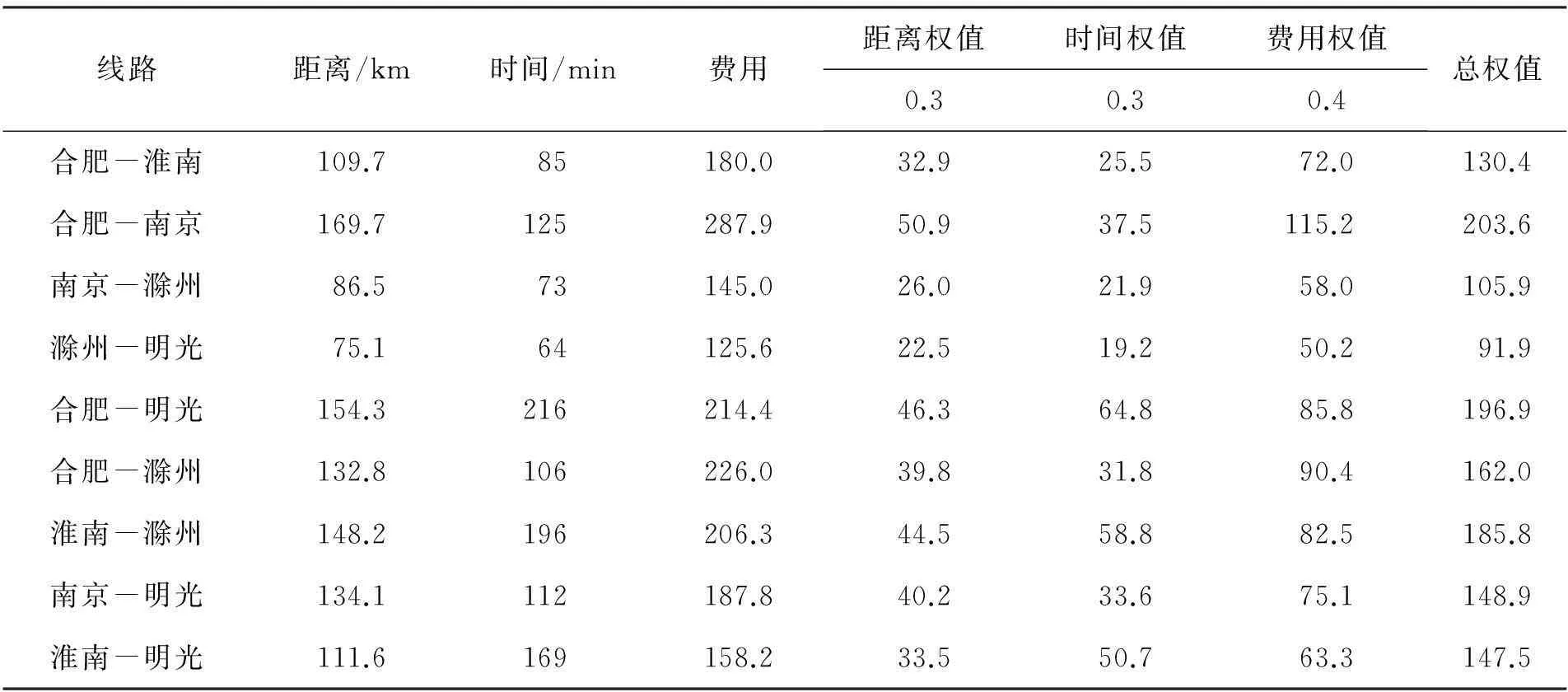
表4 城市间距离、时间、费用权值信息表
步骤3:多目标Dijkstra算法路线选择。根据以上的权值,我们利用多目标Dijkstra算法进行计算:
1)南京为已知解。与南京相连的有合肥、滁州、明光;南京-合肥权值为203.6;南京-滁州权值为105.9;南京-明光权值为148.9。所以取最小值105.9,即南京-滁州,滁州为已知解。
2)与南京和滁州相连的有合肥、淮南、明光。滁州-合肥总权值为267.9;滁州-淮南总权值为291.7;滁州-明光总权值为197.8;南京-合肥总权值为203.6;南京-明光权值为148.9。所以取最小值148.9,即路线南京-明光,明光为已知解。
3)与南京、滁州、明光相连的有合肥、淮南。南京-合肥总权值为203.6;滁州-淮南总权值为291.7;滁州-合肥总权值为267.9;明光-淮南总权值为296.4。所以取最小值203.6,即线路南京-合肥,合肥为已知解。
4)与南京、滁州、明光、合肥相连的有淮南。合肥-淮南总权值为334;滁州-淮南总权值为291.7;明光-淮南总权值为296.4。所以取最小值291.7,即线路滁州-淮南,淮南为已知解。
综上所述,配送的线路为:南京-滁州-淮南,总权值为291.7。
步骤4:“淮南-蚌埠段”费用计算。4 t货车拉货1.8 t,自重2 t,半载油耗为10 L/(100 km),由淮南开往蚌埠。
城市间相关费用表见表5。

表5 城市间相关费用表
步骤5:“淮南-蚌埠段”权值计算。城市间距离、时间、费用权值信息表见表6。
步骤6:多目标Dijkstra算法路线选择。根据以上的权值,利用多目标Dijkstra算法进行计算:
淮南为已知解。与淮南相连的有明光、蚌埠;淮南-蚌埠权值为65,淮南-明光权值为112.4。所以取淮南-蚌埠,蚌埠为已知解,权值为65。两段路线权值总计为291.7+65=356.7。

表6 城市间距离、时间、费用权值信息表
1.2.3.3方案1和方案2比较分析
方案1调度两辆2 t车两条线路总权值为456.5,方案2调度1辆4 t车的最优线路总权值为356.7。两个车辆调度方案比较得知,方案2调度1辆4 t车,总权值最小,为最佳车辆调度和最优路线。
2结语
利用Dijkstra算法实现了距离、时间和费用3个综合目标,并由此扩展到一个配送中心对应两个客户的情况,不仅实现了3个综合目标的线路设计,同时进行了合理的车辆调度[10]。配送中心或者货运企业可以根据自身状况对3个指标赋予不同的权重,针对具体业务情况进行合理的车辆调度和路线设计。
参考文献:
[1]张念.用Dijkstra算法实现对整车配送线路的优化[J].中国水运,2007,5(5):15-16.
[2]胡鹤严.基于成本的配送路线优化模型与算法研究[D]:[硕士学位论文].长春:吉林大学,2012.
[3]齐晗.对物流配送作业若干问题的优化研究[J].安徽电子信息职业技术学院学报,2012(6):22-24.
[4]南超兰.基于距离和时间的物流运输路线优化分析[J].物流科技,2012(12):65-70.
[5]杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2012(5):25-26.
[6]王静波.公路快运企业网络优化模型及算法研究[D]:[硕士学位论文].青岛:山东大学,2013.
[7]曾嘉俊.基于种群多样性的自适应变异粒子群算法及应用[D]:[硕士学位论文].成都:西南交通大学,2012.
[8]刘建美,马寿峰,马帅奇.基于改进的Dijkstra算法的动态最短路计算方法[J].系统工程理论与实践, 2011(6):78-82.
[9]张志远.基于“云计算”的智能交通系统研究与构建[D]:[硕士学位论文].兰州:西北师范大学,2011.
[10]孙瑞超.网络拓扑连通性恢复算法的研究与实现[D]:[硕士学位论文].哈尔滨:哈尔滨工业大学,2011.
Dijkstra based algorithm for
vehicle scheduling and route optimizatio
YANG Li-juan1,LIU Bo-hai2*
(1.Department of Business Administration, Anhui Business Vocational College, Hefei 231131, China;
2.School of management, Hefei University of Technology, Hefei 230009, China)
Abstract:With Dijkstra algorithm, the three business indexes in a distribution center such as distance, time and cost are integrated to build the multi-objective model. The multi-objective Dijkstra algorithm is extended with which one distribution center is responsible for two customer distribution business and vehicle scheduling.
Key words:distribution center; multi-objective; algorithm vehicle scheduling; route optimization.
作者简介:杨丽娟(1981-),女,汉族,安徽宿州人,安徽工商职业学院讲师,硕士,主要从事物流管理方向研究,E-mail:yanglj2010@163.com. *通讯作者:刘渤海(1982-),男,汉族,安徽淮北人,合肥工业大学副教授,博士,主要从事运营管理方向研究,E-mail:liubh2010@163.com.
基金项目:2013年高校省级优秀青年人才基金重点项目(2013SQRW108ZD)
收稿日期:2014-06-13
中图分类号:TP 301
文献标志码:A
文章编号:1674-1374(2015)01-0066-06
DOI:10.15923/j.cnki.cn22-1382/t.2015.1.14
