微小型救援机械手的正、逆运动学仿真分析
2016-01-29邢天羿刘春明张邦成谭海东
邢天羿, 刘春明, 张邦成*, 谭海东
(1.长春工业大学 机电工程学院, 吉林 长春 130012;
2.吉林石化公司合成树脂厂, 吉林 吉林 132000)
微小型救援机械手的正、逆运动学仿真分析
邢天羿1,刘春明2,张邦成1*,谭海东1
(1.长春工业大学 机电工程学院, 吉林 长春130012;
2.吉林石化公司合成树脂厂, 吉林 吉林132000)
摘要:应用D-H(Denavit-Hartenberg)法建立了微小型救援机械手的D-H坐标系,应用 Matlab/Robotics建立其三维仿真模型进行正运动学和逆运动学仿真。结果表明,运动过程中,微小型救援机械手的速度和加速度没有突变,能够准确、平稳地完成指定任务。
关键词:救援机械手; D-H法; 运动学
0引言
普通机器人由于空间受限等原因不能完成某些救援任务,微小型救援机器人就是为了完成这些任务而研制的特种机器人[1-2]。救援机器人不但能够协助救援人员完成救援工作,而且在一定条件下能够独立替代救援人员完成危险任务,救援工作在它们的帮助下大幅提高了效率,有效减少了救援人员的伤亡,在各种抢险救灾中发挥着越来越重要的作用[3-5]。机械手是救援机器人的核心部件,是完成一切救援工作的基础。微小型救援机械手在实际作业之前必须进行运动学分析,救援过程中还要根据基于运动学特性设计的轨迹进行控制,使实际的轨迹符合要求轨迹,以确保救援任务的顺利完成。
运动学研究是微小型救援机器人研究中一个非常重要的课题[6],许多国内外的专家和学者在这方面做了大量的工作。为了使微小型救援机器人在危险、特殊环境下仍能完成特定工作,对运动学分析的深度要求不断提高。在机器人运动学的研究中,涉及大量并且复杂的计算[7],应用软件对机器人进行运动仿真,可以大量节约人力和时间,提高工作效率,并且由仿真结果中可以清晰看出机器人的运动情况,得到许多控制的重要信息和规律。
D-H法是Denavit和Hartenberg在1955年提出的一种使用矩阵建立关节链中每一个杆件的附体坐标系的方法[8-9],文中采用D-H法[8]建立微小型救援机械手的坐标系,应用Matlab软件中的Robotics工具箱[10]对微小型救援机械手进行三维建模、运动学求解和仿真,应用Robotics工具箱极大地降低了运动学求解的难度和计算量,验证了微小型救援机械手空间运动轨迹的合理性。
1微小型救援机械手的D-H参考坐标系的建立及D-H参数的确定
微小型救援机械手由5个旋转关节组成,每个关节由一个舵机进行驱动,舵机转动采用脉冲调制技术控制,处理器为STM32嵌入式处理器,机械手的结构如图1所示。

图1 微小型救援机械手
机械手的转动机构可以实现机械手整体旋转,与机械手的移动结构固连。大臂在舵机的带动下可以上下摆动。机械手小臂与大臂前端相连接,在舵机的带动下做俯仰运动。机械手的腕部位于小臂的前端,可在舵机的驱动下转动。
在执行救援任务中,微小型救援机械手的动作必须准确,要精确控制机械手的多个关节协调运动以达到准确的效果,就必须要准确的建立机械手的运动学模型,合理描述微小型救援机械手各关节之间的位置关系,方便控制算法的设计。文中选用现今机器人领域应用较多的D-H法建立坐标系[11-12],如图2所示。

图2 微小型救援机械手连杆坐标系
其中X0,Z0为基准坐标系坐标轴,Z1~Z5表示5个关节的转动轴,x轴的方向为Zn和Zn-1之间公垂线指向Zn的方向,y轴按右手规则确定,由于文中没有使用,所以未在图2中标注。关节在不同坐标系之间的转换采用矩阵法,矩阵法是研究机器人运动学的较常用方法,文中采用四阶齐次矩阵T进行坐标变换,公式如下:

式中:A----旋转角度变换;
B----位置矢量变换。
根据微小型救援机械手的机械结构和尺寸得到D-H参数表,见表1。

表1 微小型救援机械手的D-H参数表
表中θi为绕xi轴zi到zi+1的角度,di为连杆长度,ai为沿zi轴xi-1到xi的距离,αi为绕zi轴xi-1到xi的角度。采用右手规则确定正负方向。
2微小型救援机械手的仿真模型建立
应用Matlab中的Robotics工具箱[13-14]以及微小型救援机械手的参数建立微小型救援机械手的运动学仿真模型,仿真三维图如图3所示。

图3 微小型救援机械手三维模型
通过使用控制面板中的滑块可以模拟微小型救援机械手的运动,操作方便、十分直观,微小型救援机械手的仿真模型控制面板如图4所示。

图4 微小型救援机械手的仿真模型控制面板
通过使用滑块可以模拟微小型救援机械手的运动。
利用Matlab中的LINK函数对微小型救援机械手进行建模的主要程序如下:
L1=link([-pi/2 22 0 0 0]);
L2=link([0 79 0 0 0]);
L3=link([0 80 0 0 0]);
L4=link([pi/2 50 0 0 0]);
L5=link([0 0 0 0 0]);
r=robot({L1L2L3L4L5});
r.name='微小型救援机械手';
drivebot(r);
3微小型救援机械手的正运动学仿真
微小型救援机械手的正运动学是指已知微小型救援机械手各关节的参数,求解微小型救援机械手末端的位姿。选取微小型救援机械手各关节的初始变量即每个关节的关节角度,记为q1=(0 0 0 0 0),操作机械手的驱动滑块,记录每一次每个关节的关节变量,共记录31组数据,拟合后曲线如图5所示。

图5 关节角度位移变化图
使用Fkine命令结合滑动模块,设定运动总时间(t=3s),时间间隔0.1s,得到微小型救援机械手末端在每个时刻的位姿矩阵如下:

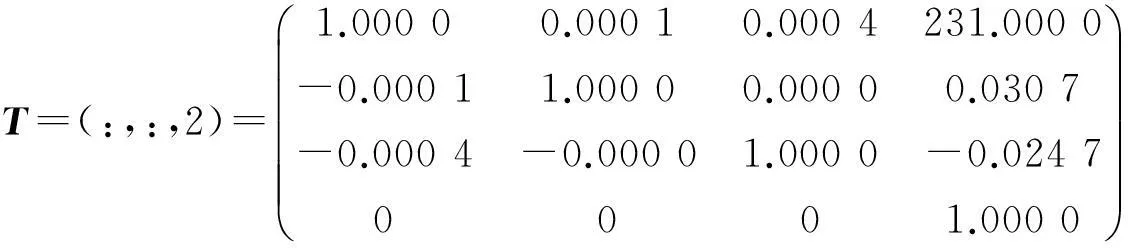

⋮

由以上矩阵可得微小型救援机械手末端连杆坐标系相对于基坐标系的位置,计算过程简便,验证了运动学正解的唯一性和确定性。微小型救援机械手末端的位移曲线如图6所示。
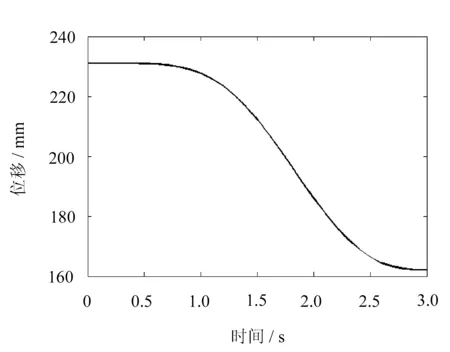
(a) 在x轴方向上的位移
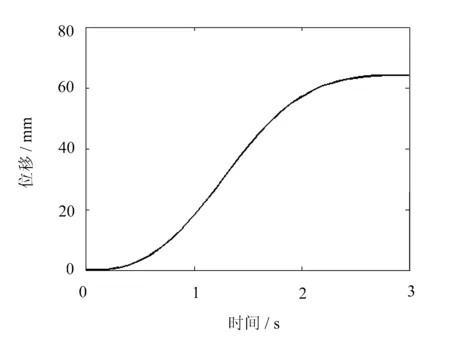
(b) 在y轴方向上的位移
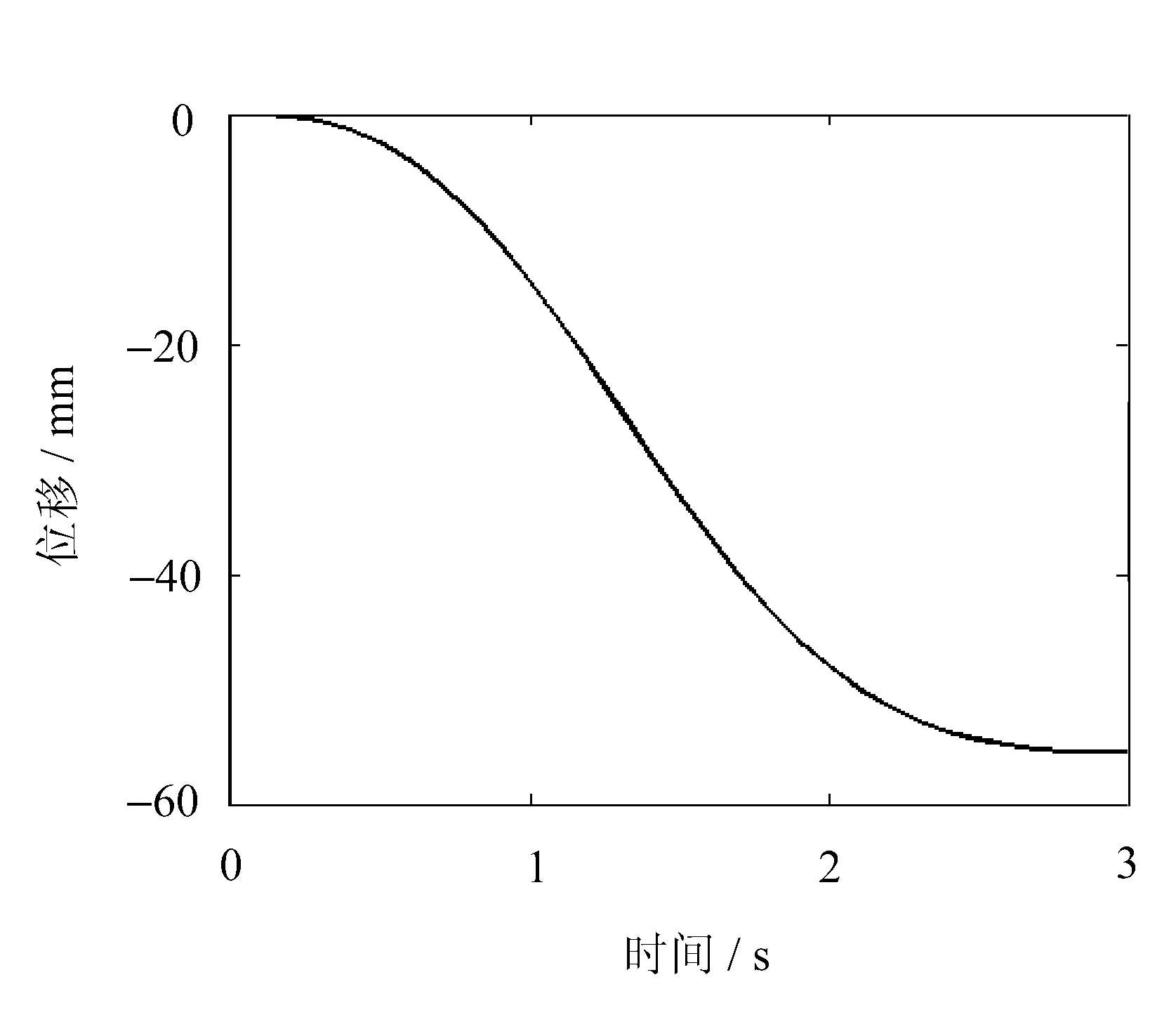
(c) 在z轴方向上的位移图6 微小型救援机械手末端位移曲线
由图6可以看出,在笛卡尔空间坐标系中,微小型救援机械手由初始位姿运动到最终位姿,其末端在沿x轴方向上移动了-69.119mm,在沿y轴方向上移动了64.1854mm,在沿z轴方向上移动了-55.449mm。
4微小型救援机械手的逆运动学仿真
微小型救援机械手的逆运动学是要求解当机械手末端到达某个位置时,与这个位置有关的各个关节的位置[15]。逆运动学求解的过程十分复杂,计算量很大。微小型救援机械手逆运动学的仿真选取以上正运动学的初始状态和终止位姿

应用Matlab中Jtraj函数,该函数采用的是7次多项式差值。
微小型救援机械手各关节角的变化情况如图7所示。

图7 微小型救援机械手各关节角速度变化图
通过该图的仿真曲线可以看出,微小型救援机械手从点q1运动到点q2的过程中各关节的运动情况,且各关节的运动情况均正常,无错位现象。
微小型救援机械手各个关节的速度变化曲线和加速度变化曲线分别如图8和图9所示。
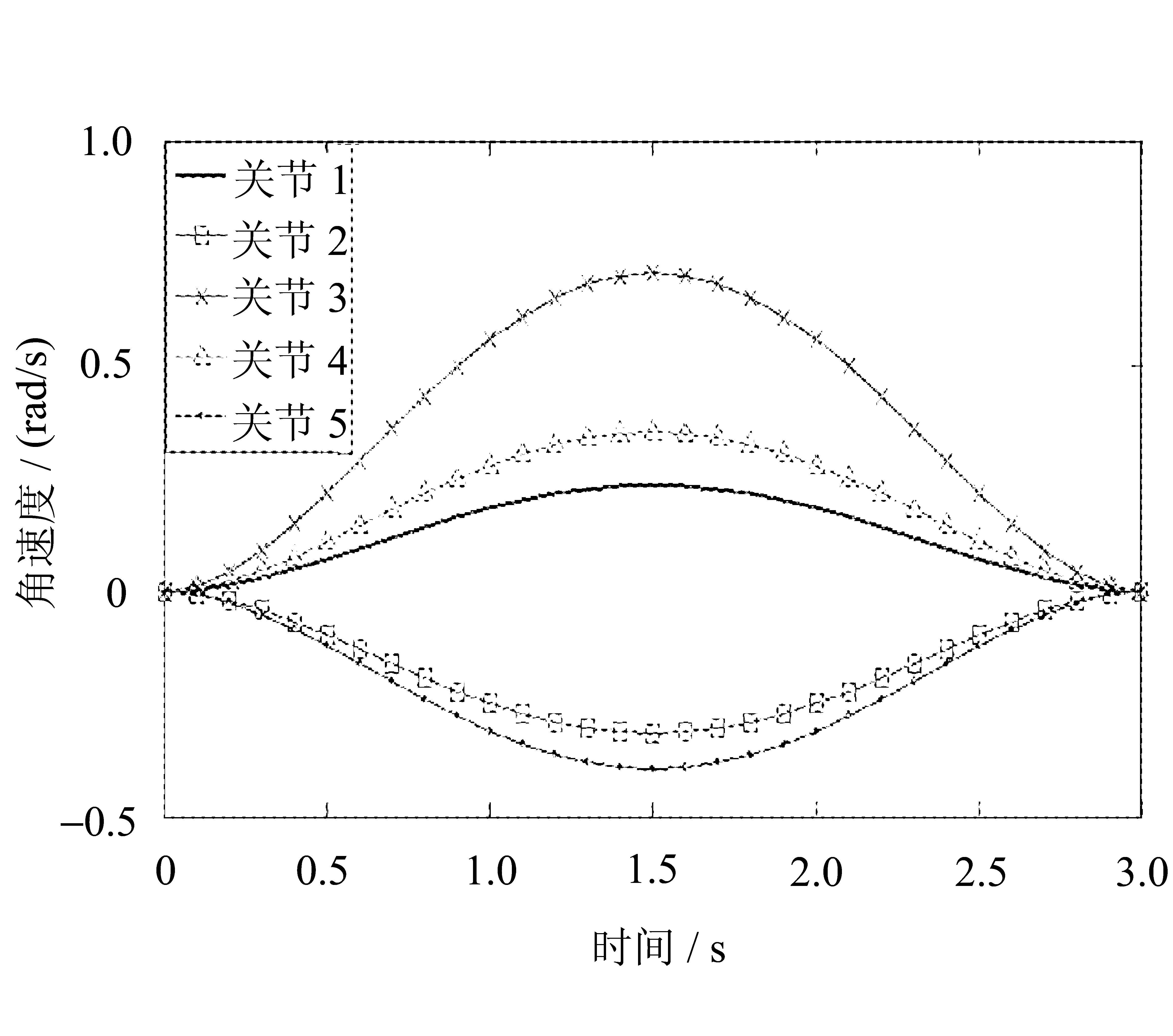
图8 微小型救援机械手各关节角速度变化图
由图中可以看出,各关节的角速度和角加速度仿真曲线连续、光滑,这表明微小型救援机械手的运动稳定、无突变,有助于机械手颤动、机械手末端执行器达不到指定的位姿等不良问题的解决。

图9 微小型救援机械手各关节角加速度变化图
5结语
文中应用D-H法建立了微小型救援机械手的D-H坐标系,确定了微小型救援机械手的各关节D-H参数。基于Matlab的Robotics工具箱,建立了微小型救援机械手的三维仿真模型,提高了微小型救援机械手运动学仿真的灵活性、直观性、操作性。通过使用Robotics工具箱中的命令进行了正运动学和逆运动学求解,很大程度上加快了计算的速度,提高了运算效率,并绘制了微小型救援机械手的各个关节角速度和角加速度变化曲线,结果表明,微小型救援机械手运动过程稳定,为下一步精确的控制微小型救援机械手和实现工作空间任意动作奠定基础。
参考文献:
[1]王树国,付易利.我国特种机器人发展战略思考[J].自动化学报,2002,28:70-76.
[2]张明路,彭平,张小俊.特殊环境下服役机器人发展现状及其关键技术研究[J].河北工业大学学报,2013(1):70-75.
[3]刘金国,王越超,李斌,等.灾难救援机器人研究现状、关键性能及展望[J].机械工程学报,2006,42(12):1-12.
[4]J Casper, R Murphy. Human-robot interaction during the robot-assisted urban search and rescue response at the world trade center[J]. IEEEE Transaction on System, Man, and Cybernetics-Part B: Cybernetics,2003,33(3):367-383.
[5]李宇波,朱效洲.救援机器人技术研究进展[J].机器人技术与应用,2011,6:6-12.
[6]刘巧红,刘军,刘广瑞.矿山机器人的研究现状与发展趋势[J].矿山机械,2009,37(24):45-48.
[7]罗家佳,胡国清.基于Matlab的机器人运动学仿真[J].厦门大学学报:自然科学版,2005,44(5):640-644.
[8]蔡自兴.机器人学基础[M].北京:机械工业出版社,2009.
[9]J Denavit, R S Hartenberg. A kinematic notation for lower pair mechanisms based on matrices[J]. Journal of Appied Mechanics,1955,22:215-221.
[10]谢斌,蔡志兴.基于MATLAB ROBOTICS TOOLBOX的机器人学仿真实验教学[J].计算机教育,2010,19:140-143.
[11]牛元会,程光明,杨志刚.D-H坐标系下机械手正向运动学分析[J].机器人技术,2006(7):27-29.
[12]Z M Bi, W J Zhang, I M Chen, et al. Automated generation of the D-H parameters for configuration design of modular manipulators[J]. Robotics and Computer-Integrated Manufacturing,2007,23(5):553-562.
[13]P Corke. A robotics toolbox for MATLAB[J]. IEEE Robotics and Automation Magazine,1996,3(1):24-32.
[14]邢广成,张洛花.基于MATLAB的PUMA机器人运动仿真研究[J].高新技术,2011,80:5-7.
[15]程永伦,朱世强,刘松国.基于旋转子矩阵正交的6R机器人运动学逆解研究[J].机器人,2008(2):160-164.
Forward and inverse kinematics simulation of
miniature rescue manipulator
XING Tian-yi1,LIU Chun-ming2,ZHANG Bang-cheng1*,TAN Hai-dong1
(1.School of Electrical & Electronic Engineering, Changchun University of Technology, Changchun 130012, China;
2.Jilin Detrochemical Company Synthtic Resin Factory, Jilin 132000, China)
Abstract:D-H coordinate system of a miniature rescue manipulator is established with D-H (Denavit-Hartenberg) method, and the 3D model of the manipulator is built in MATLAB/Robotics for both the forward and inverse kinematics simulation. The results show that no sharp changes in velocity and acceleration, so the manipulator can move and stop smoothly with high precision.
Key words:rescue manipulator; D-H method; kinematics.
作者简介:邢天羿(1981-),男,汉族,黑龙江鸡西人,长春工业大学硕士研究生,主要从事机电检测与控制方向研究,E-mail:vincentxing1001@163.com. *通讯作者:张邦成(1972-),男,汉族,吉林长春人,长春工业大学教授,博士,主要从事机电检测与控制方向研究,E-mail:zhangbangcheng@ccut.edu.cn.
基金项目:吉林省教育厅“十二五”项目(2013153)
收稿日期:2014-10-14
中图分类号:TP 272
文献标志码:A
文章编号:1674-1374(2015)01-0011-06
DOI:10.15923/j.cnki.cn22-1382/t.2015.1.03
