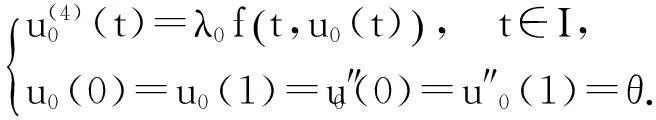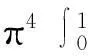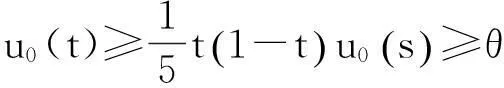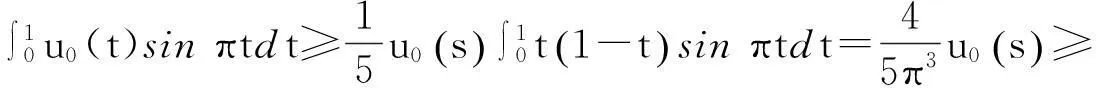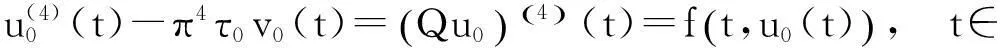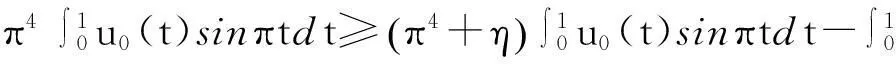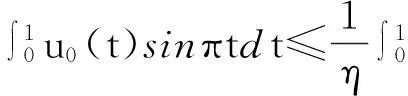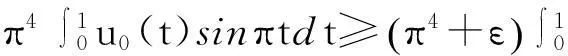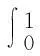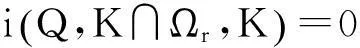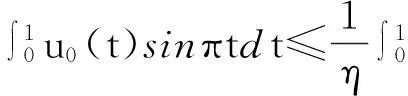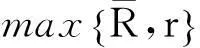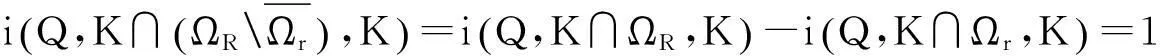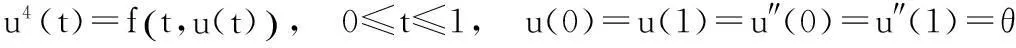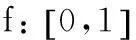Banach空间四阶两点问题正解的存在性

李伟鹏，　李小龙

(陇东学院数学与统计学院， 甘肃庆阳745000)



Banach空间四阶两点问题正解的存在性

李伟鹏，李小龙

(陇东学院数学与统计学院， 甘肃庆阳745000)

[摘要]讨论了Banach空间E中的四阶边值问题:

[关键词]四阶边值问题； 闭凸锥； 正解； 凝聚映射； 不动点指数

1引言与主要结果

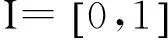
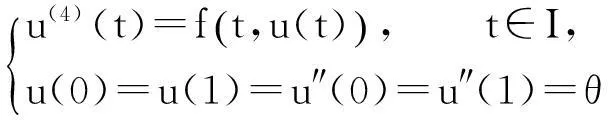
(1)

正解的存在性.其中f∶I×P→P连续.

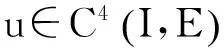
Banach空间的常微分方程与普通常微分方程的最大差异是,把微分方程转换为与之等价的积分方程后,相应的积分算子不再具有紧性,为了对该积分算子应用凝聚映射的不动点理论,通常需要给f附加一些非紧性测度条件.文献[2]使用了如下的非紧性测度条件:

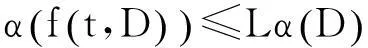
在条件(P0)下文献[2]用严格集压缩算子的锥拉伸与锥压缩不动点理论,证明了f满足下列增长条件

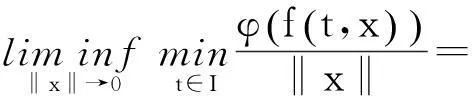
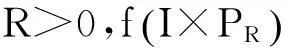
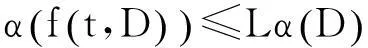
另一方面，文献[2]中的极限形式条件(P1)在Banach空间E中不如序条件易于检验和使用,故本文将使用序条件代替(P1).

本文的主要结果为

定理1设E为Banach空间,其正元锥P为正规锥,f∶I×P→P连续,满足条件(H0).若f满足下列条件之一:

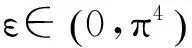
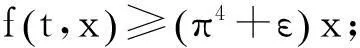
定理1中的π4是方程(1)对应的线性边值问题的第一特征值,同时删去了f的一致连续性.将此结果作到了最优. 所得结果改进了文献[1-4]中的相关结论, 并将文献[5]中的结果推广到了无穷维空间.

2预备知识

定义算子Q∶C(I，P)→C(I，P)如下：

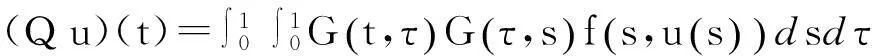
(2)

其中G(t,s)为相应的线性边值问题: -u″=θ, u(0)=u(1)=θ的Green函数

(3)

则Q∶C(I，P)→C(I，P)连续, 且方程(1)的解等价于积分算子Q的不动点.

‖un(t)‖≤ψ(t)a.e,t∈I, n=1,2,…，

引理4设f∶I×P→P满足(H0),则由(2)式定义的算子Q∶C(I，P)→C(I，P)为凝聚映射.

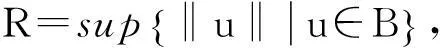
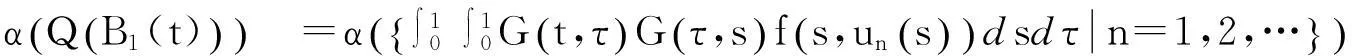
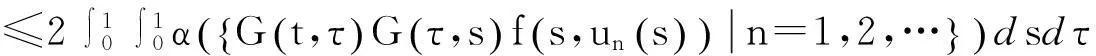
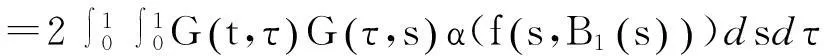
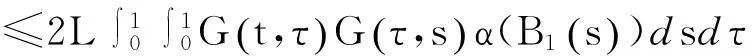
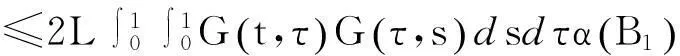
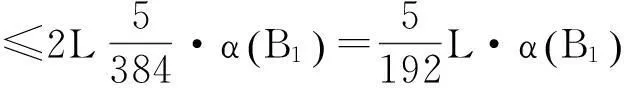
于是有

因此Q∶C(I，P)→C(I，P)为凝聚映射.

由(3)易知,Green函数G(t,s)具有性质:

(i) 0≤G(t,s)≤G(s,s),t,s∈I;

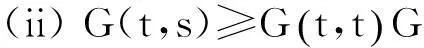
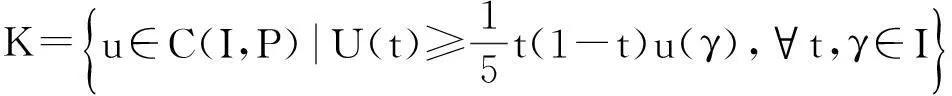
(4)

证对∀u∈C(I，P),及∀t,γ∈I,由(2)式和性质(i)有

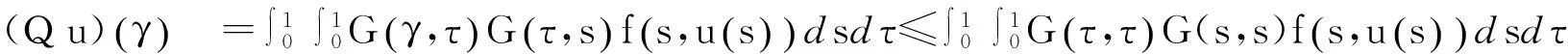
又由(2)式和性质(ii)有

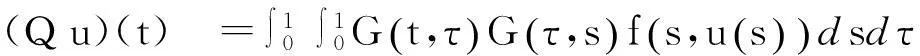
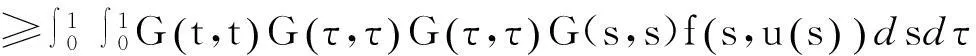
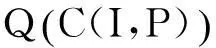
从而当f∶I×P→P时,Q∶K→K为凝聚映射,方程(1)的正解等价于Q在K中的不动点.本文将用凝聚映射的不动点指数理论寻找Q的不动点.

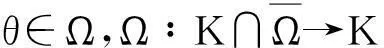
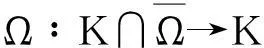
下面用引理6与引理7证明本文的主要定理

3主要结果的证明

定理1的证明由上面的论述知,只需证明由(2)式定义的凝聚映射Q∶K→K存在非零的不动点.取0

情形1f满足假设(H1). 取0

u≠λQu,∀u∈K∩∂Ωr, 0<λ≤1，

(5)

反设(5)式不成立,则存在u0∈K∩∂Ωr及0<λ0≤1,使得u0=λ0Qu0.按Q的定义,u0满足微分方程:

(6)

方程(6)第一式两边同乘以sinπt,在I上积分,并应用假设(H1)之(i),有

因为0<ε<π4,故由上式有

另一方面,因为u0∈K,按锥K的定义,

两边同乘以sinπt,在I上积分,得

(7)

(8)

u-Qu≠τv0,∀u∈K∩∂ΩR,τ≥0.

(9)

反设存在u0∈K∩∂ΩR及τ0≥0,使得u0-Qu0=τ0v0,按算子Q的定义u0满足微分方程:

(10)

按假设(H1)之(ii)，有

注意到u0=τ0v0+Qu0满足边界条件u(0)=u(1)=u″(0)=u″(1)=θ,将上式两边同乘以sinπt在I上积分得

从而有

上式结合(7)式，有

由锥P的正规性,有

(11)

情形2f满足假设(H2). 取0

u-Qu≠τv0,∀u∈K∩∂Ωr,τ≥0.

(12)

其中v0(t)=esinπt∈K,反设(12)式不成立,则存在u0∈K∩∂Ωr及τ0≥0,使得u0-Qu0=τ0v0,于是u0(t)满足微分方程(10).由(10)式及假设(H2)之(i)有,

上式两边同乘以sinπt在I上积分得

因此

(13)

再证当R充分大时,有

u≠λQu,∀u∈K∩∂ΩR,0<λ≤1.

(14)

假设存在u0∈K及0<λ0≤1,使得u0=λ0Qu0,则u0满足微分方程(6).将方程(6) 两边同乘以sinπt在I上积分,并应用假设(H2)之(ii)得

从而有

于是该式结合(13)式有,

[参考文献]

[1]吕志伟.Banach空间中一类四阶常微分方程两点边值问题的最大解和最小解的存在性[J].应用泛函分析学报,2005,7(4):370-374.

[2]张学梅.Banach空间中四阶常微分方程边值问题的正解[J].数学的实践认识,2007,37(20):150-155.

[3]冯麦强,葛渭高.Banach空间中四阶方程边值问题的正解[J].数学的实践认识,2007,37(21):141-147.

[4]吕志伟.Banach空间中一类四阶奇异边值问题的解的存在性[J]. 数学的实践认识,2008,38(24):195-199.

[5]Bai Z,Wang H.On positive solutions of some nonlinear fourth-order beam equations [J]. J Math Anal Appl.2002,270:357-368.

[6]郭大钧,孙经先.抽象空间常微分方程[M]. 济南:山东科学技术出版社,1989:188-222.

[7]HEINZ H R.On the behaviour of measure of noncompactness with respect to differention and integration of vector-valued functions [J].Nonlinear Anal,1983,7(12):1351-1371.

[8]李永祥.抽象半线性发展方程初值问题解的存在性[J]. 数学学报,2005,48(6):1103-1108.

[9]郭大钧.非线性泛函分析 [M].济南:山东科学技术出版社,1985:234-353.

[10]余庆余.半序Banach空间中凝聚映射及其正不动点 [J].兰州大学学报(自然科学版),1979,15(3):1-5.

Existence of Positive Solutions for Fourth-OrderTwo-Point Boundary

Value Problems in Banach Spaces

LiWei-pengLiXiao-long

(College of Mathematics and Statistics, Longdong University, Qingyang Gansu 745000,China)

Abstract:The existence of positive solutions for fourth-order boundary value problem

Key words:fourth-order boundary value problem ; closed convex cone; positive solution; condensing mapping; fixed point index

[中图分类号]O175.15

[文献标识码]C

[文章编号]1672-1454(2015)05-0083-06

[基金项目]甘肃省高等学校科研项目(2013B-086)； 陇东学院青年科技创新项目(XYZK1109)

[收稿日期]2014-09-30