围线积分的计算及巧妙运用

滕岩梅

(北京航空航天大学数学与系统科学学院，北京100190)



围线积分的计算及巧妙运用

滕岩梅

(北京航空航天大学数学与系统科学学院，北京100190)

[摘要]围线积分的计算在复变函数与积分变换中被广泛使用，对后继课程的学习非常重要. 本文将积分计算中需注意的问题和计算方法详加总结,并应用柯西积分定理解决一些复杂问题.

[关键词]围线积分； 单连通区域柯西积分公式； 柯西积分定理； 高阶导数公式

1引言

围线积分是复变函数与积分变换的主要内容之一，其应用也非常广泛，在工程中很多领域都有涉及.首先，阐述围线积分的几种计算方法.

2围线积分的计算

首先要注意被积函数解析性，可分下面几种情况：

2.1　被积函数在积分区域内处处解析，在区域内部及边界上连续

解因为被积函数在整个复平面上有两个不解析的点，均在积分区域外部. 由单连通区域内的柯西积分定理，积分值为零.

此积分看起来似乎可以用参数方程计算定积分的方法，但明显计算上要复杂得多.

2.2　被积函数在积分区域D内有一个不解析的点，在积分曲线上连续

此时可根据被积函数的表示形式，用不同的公式运算.

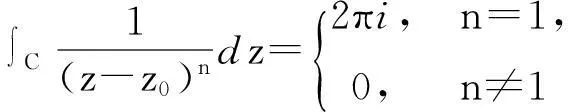
求解,其中C为包含z0的任意封闭曲线.

解由重要公式知

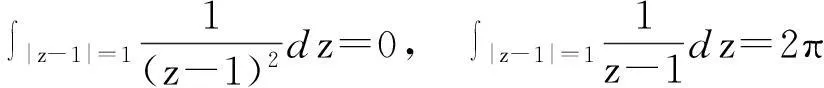
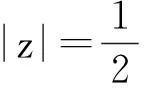
求解,其中C为包含z0的任意封闭曲线.

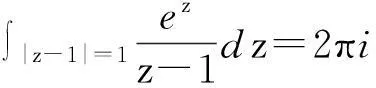
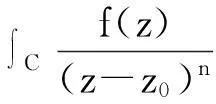
求解,其中C为包含z0的任意封闭曲线.

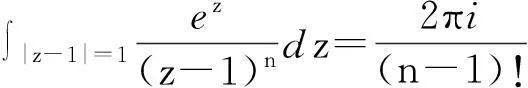
2.3　被积函数在积分区域内有有限个奇点，在积分内部及曲线上连续

这时，需要用多连通区域的柯西积分定理,将沿原曲线积分转化为沿小曲线积分和，每个小曲线内只包含被积函数的一个不解析的点. 然后用相应公式求解.

解分别以0，1为心做互不包含、互不相交的小圆C1,C2，则

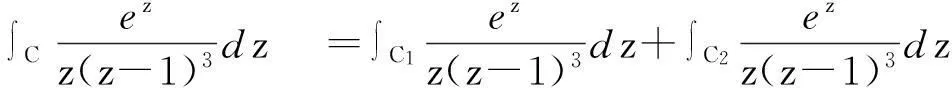
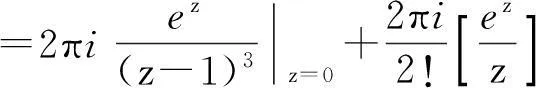
2.4　用留数求围线积分

当被积函数在复平面内有有限个奇点或在积分区域内有有限个奇点时，可以用留数方法计算围线积分，围线积分对被积函数的形式没有其他要求，因此应用相对广泛.

上面我们举的围线积分的例子，都可以用留数方法计算.

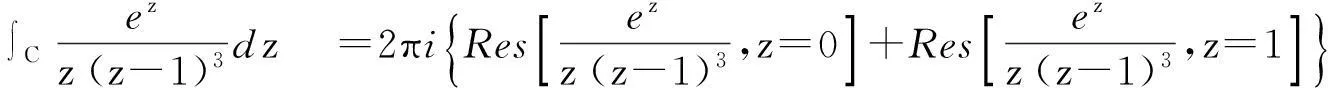
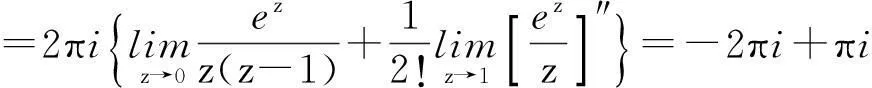
此外，对某些不能用上面方法计算的围线积分，只要满足留数定理的要求，就可以用留数方法计算.

解因为被积函数在积分区域内只有一个奇点0，所以

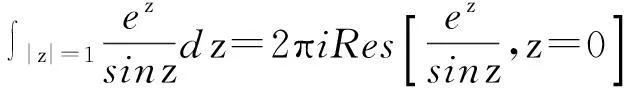
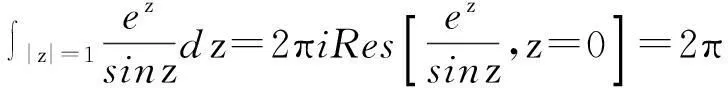
3巧用柯西积分定理

3.1　简化积分计算

单连通区域柯西积分定理被称为单复变的钥匙，在理论体系的建立方面其重要性不容忽视.利用这一定理可以引入不定积分,简化计算，此定理的推广形式：多连通区域柯西积分定理可以帮助解决更多围线积分问题.

此定理也是计算复积分的切实有效的方法.对于一些复杂的复积分，可以利用单连通区域的柯西积分定理,将之转化为简单积分或已知积分进行运算.

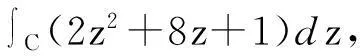
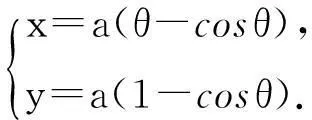
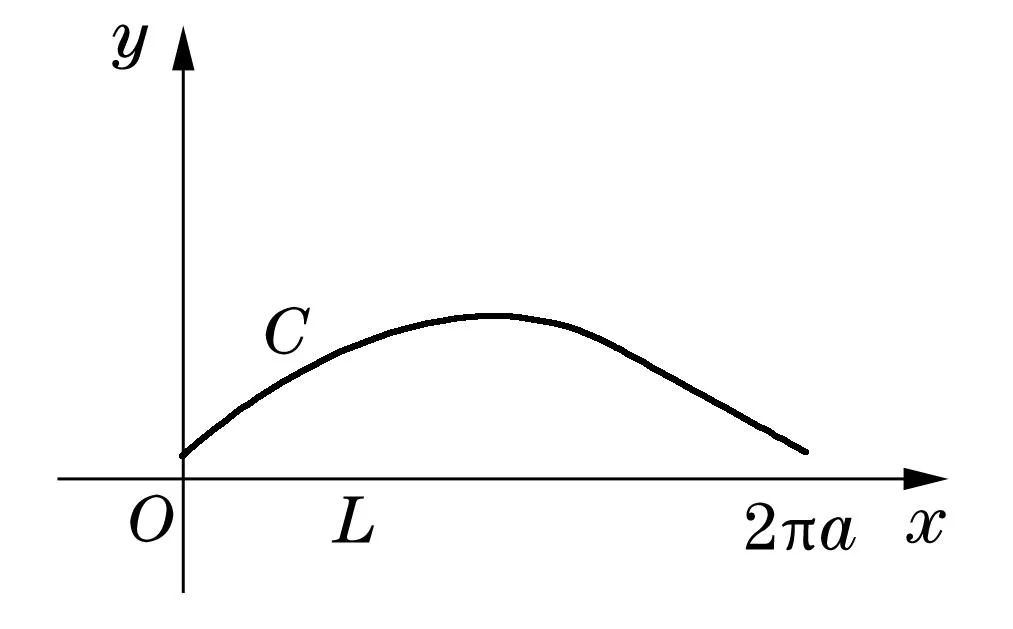
图1

解由图1知，直线段L与C构成一条闭曲线.因为2z2+8z+1在全平面上解析，则

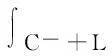
即

这样，把函数沿曲线C的积分化为沿着直线段L上的积分.由于

解由傅立叶变换的定义，f(t)的傅立叶变换为

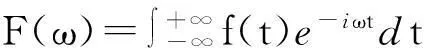
则

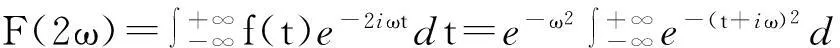
令z=t+iω，得

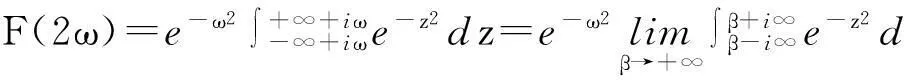
这是一个复变函数的积分，取如图2所示的闭曲线C=C1+C2+C3+C4，有

∫Ce-z2dz=∫C1+C2+C3+C4e-z2dz=0.

因为当β→+∞时，有

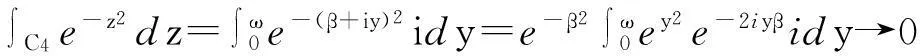
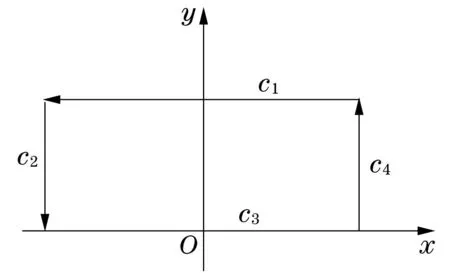
图2

同理得∫C2e-z2dz→0. 又由已知条件知,当β→+∞时，

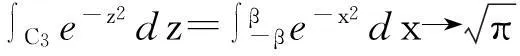
所以

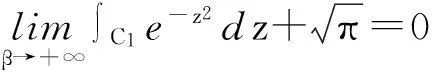
即

3.2　用单连通区域柯西积分定理求实积分

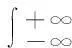
定理2设f(z)在整个复平面Z上除有限个奇点外均解析,且这些奇点不在实轴上.如果存在一个常数M与正数R以及α>1,使得对于一切|z|≥R,有

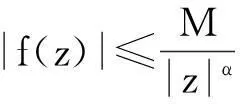
成立,则

其中zk是f(z)上半平面的奇点.

证令r>R,考虑曲线Cr=[-r,r]∪Γr,其中Γr为上半圆周，使得f(z)在上半平面内的全部奇点都包含在Cr中,于是由留数定理有

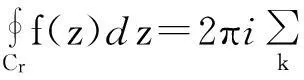
其中zk是f(z)上半平面的奇点.

左边的积分又等于

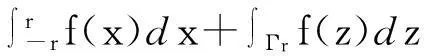
所以

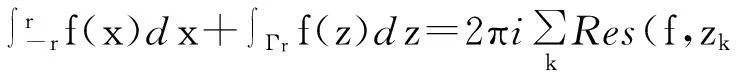
(1)

对于上述等式,如果令r→+∞,由于Cr的作法,知Cr内部不会再有增加的奇点,所以(1)式右端保持不变.由

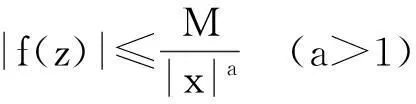
|x|≥R时,f(x)在x∈R上可积,所以(1)式左边的第一个积分当r→+∞是存在的,即

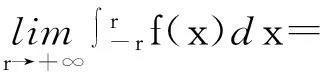
为了证明结论成立,我们只须证明,当r→+∞,(1)式左端第二个积分趋于零,因为

但

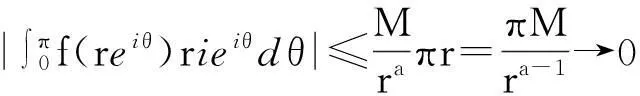
所以当r→ +∞

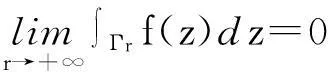
3.3　多连通区域柯西积分定理的应用

拉普拉斯逆变换公式为

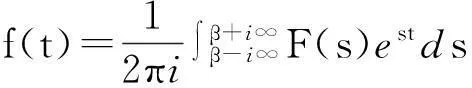
是一个复积分. 通常计算会较为困难. 但满足合适条件时，可以用留数方法求解. 而此定理证明用到了多连通区域柯西积分定理.

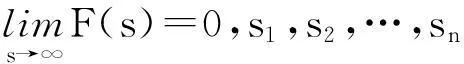
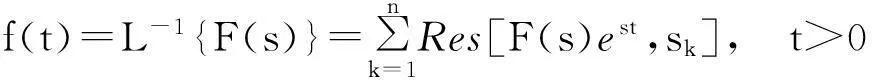
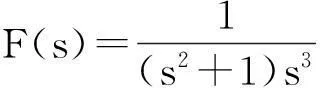
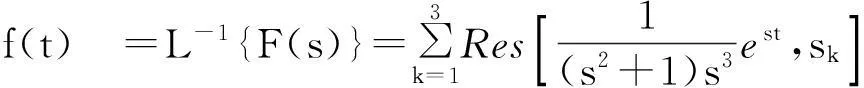
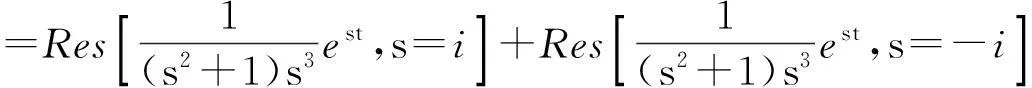
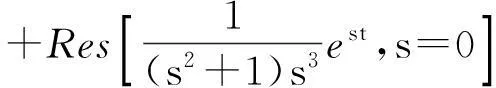
此外，工程中常用的z变换，其反z变换实质即为计算围线积分[3]. 公式为

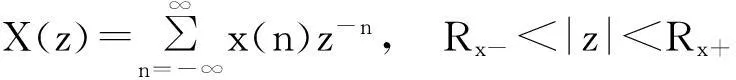
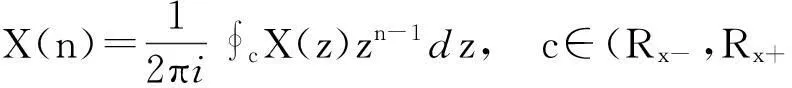
解由反z变换的公式以及求围线积分的留数定理，有

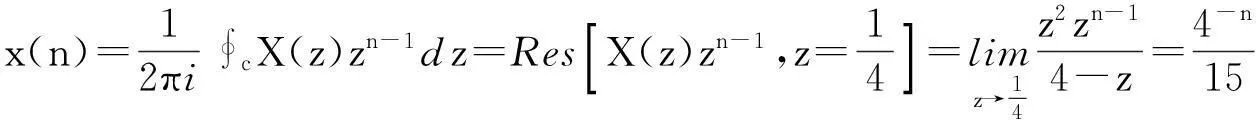
4结论

围线积分在许多学科分支、应用领域都有着广泛应用.而对于其计算除了上述方法外，我们还有级数法等，在此不一一列举.

[参考文献]

[1]高宗升，滕岩梅. 复变函数与积分变换[M].5版.北京：北京航空航天大学出版社，2010.

[2]Saff E B,Snider A D. Fundamentals of Complex Analysis With Applications to Engineering and Science[M]. Beijing：China Machine Press，2005.

[3]张华林，周小方.“信号与系统”课程逆z变换的两个方法[J]. 漳州师范学院学报，2013(2)：47-49.

Computation of Contour Integeral and Flexible Application

TENGYan-mei

(School of Mathematics and Systems Science, Beihang University, Beijing 100191,China)

Abstract:The calculation of contour integral has been widely used in the complex variable function and the integral transform,and it is important to the subsequent course. In this paper,the problems that we should pay attention in integral calculation and the computational method are summarized. Some complex problems are solved by Cauchy integral theorem.

Key words:contour integral； Cauchy integral figure； Cauchy integral theorem； higher derivative figure

[中图分类号]O177.6

[文献标识码]C

[文章编号]1672-1454(2015)05-0066-06

[基金项目]北京航空航天大学重点教改项目(201413)； 北京航空航天大学重大教改项目(4303013)

[收稿日期]2015-06-10