美国大学数学询问式教学法的过去和现在

韩舒平,　鲁　斌,　杜淑仪,　钟建媛

(1. 美国纽约城市理工大学数学系, 纽约11201；

2. 美国加利福尼亚州州立大学萨克拉门托分校数学统计系, 萨克拉门托95819;

3. 美国密执安大学Flint校区数学系, 密执安48502)



美国大学数学询问式教学法的过去和现在

韩舒平1,鲁斌2,杜淑仪3,钟建媛2

(1. 美国纽约城市理工大学数学系, 纽约11201；

2. 美国加利福尼亚州州立大学萨克拉门托分校数学统计系, 萨克拉门托95819;

3. 美国密执安大学Flint校区数学系, 密执安48502)

[摘要]以询问式为基础的数学教学方法在美国大学数学教学中是一个著名的方法.这个方法起源于美国著名数学家摩尔博士.与传统授课方式不同，这个方法著重于培养学生独立获取知识，独立思考，创造和批判式思维方面的能力.作者在本文对于询问式教学法及课堂运用进行介绍，给出几个典型使用此方法设计课程的实例，并对在运用中可能出现的问题做出讨论.

[关键词]摩尔方法; 修改的摩尔方法; 询问式教学

1询问式教学的过去和现状

在美国大学数学教学中，使用以询问式为基础的教学方式(Inquiry-Based Learning 或简称 IBL)来进行教学已经有多年的历史.这种教学法起源于美国著名数学家摩尔博士(Moore, 1882-1974)，所以著称为摩尔方法 (Moore Method).另外这个教学方法还被称为：苏格拉底式，德克萨斯式，演绎式，由发现来学习式，或边做边学习方式等[9].以询问式为基础的教学法主要强调培养学生独立获取知识，独立思考，创造和批判式思维方面的能力.因此授课教师在使用此方法教学时，着重点放在培养学生对课程的深入理解和学生的研究和创造能力.

摩尔博士从1920起在德克萨斯大学工作了半个世纪，他在许多不同类别的大学数学课程中都使用以询问式为基础的教学方法.从本科生微积分到研究生拓扑学，摩尔博士都使用这个教学法.摩尔博士认为：在教学中直接传授给学生的越少教学效果就会越好[14].在教学中，摩尔博士的课既不用教材，也很少直接讲授课程；他使用自己为课程所精心设计的问题集，要求学生独立解决问题集中的每一个问题，并且在课堂上来向其他同学阐述自己对问题的解答或证明.此外他还要求学生对所给出问题的解答或证明进行评估，对其正确性进行审核.因为课程着重强调独立思考和独立解决问题，所以学生之间的讨论和相互帮助是不允许的；此外他还规定禁止使用图书馆或资料室来查相关资料.摩尔博士是使用此方法教学的大师，如仅从成功的学生来衡量教学质量的话，摩尔博士也许是历史上最优秀的数学老师[6]：在他50个博士毕业生中，其中许多都是出色的数学家，比如有3人(Wilder, Whyburn, Bing) 曾任美国数学学会主席，有3人曾任副主席 (Moise, Anderson, Rudin); 5人曾任美国数学协会主席 (Anderson, Moise, Young, Bing, Wilder)；他和他的3个学生 (Whyburn, Wilder, Bing) 都当选为美国国家科学院士.

除了摩尔方法外，还有更普遍使用的以询问式为基础的教学法——修改的摩尔方法(Modified Moore Method 或MMM)[14，5].修改的摩尔方法不象摩尔方法要求或限制那样严格，比如在教学中可使用教材，学生之间也可以进行讨论.有时学生可以分成小组，协同合作解决问题.在当今美国大学数学教学中，以询问式为基础的教学法有着比较广泛的含义，但是摩尔方法中学生独立思考和解决问题的特征是贯穿在课程当中的.学生作为整个学习过程的中心，在学习过程中积极致力于发现和获取课程内容，解决课程中的问题，通过语言，文字来论证和解答所提供的问题，这是以询问式为基础教学的基本点，也是跟传统以授课为基础的教学方式的主要不同点.运用以询问式为基础教学法的课程也不仅仅局限于以证明为主的数学课程(例如数学分析，抽象代数，拓扑课程)，此教学法还用在其它象微积分，文科数学，统计等非理论性的应用课程[18].近年来，在有些大学里，物理，化学等课程也采用以询问式为基础的教学法，还有一些中学也使用此教学法进行数学教学.

在下文中，我们介绍使用询问式教学法的课程设计和运用并给出几个典型实例.此外，我们对于实施这个方法在教学中可能遇到的一些问题和处理方案做出讨论.

2以询问式为基础的教学

通常以询问式为基础的教学法是指在课程中以学生为中心和主体，让学生积极参与进而做出有理结论的活动.任课教师不是直接在课堂上讲授课程中内容观念也不直接给出问题的解答或证明，而是通过为课程精心设计的一系列问题来引导学生对课程进行探索和发现.学生的任务包括解题，做出推测，试验，探索，创造和交流等数学工作者常具有的技能和习惯.以询问式为基础的教学法使得学生，课程，学生和课程之间的互动成为学习的中心.同时，这个方法把任课教师的作用从直接传递知识变成在学习过程中的引导和辅助作用.其目的是通过学生在课程学习中的积极主动性和责任感，来激发学生对学习的热情和对知识的渴望，并培养学生独立获取和理解课程知识的能力.

以询问式为基础教学的课程设计

在使用以询问式为基础的教学法进行教学之前，任课教师常常需要进行大量的准备工作——即要对课程重新设计：将课程内容重新思考，重新组织调整.要确定该课程中哪些内容是不可缺少或省略的核心内容；其次还要确定对学生的期望和要求，即学生在修完这门课后，他们应该掌握哪些必备知识和能力.在此基础上将所定下来的课程内容进行分析，设计和编写课程所使用的问题集.这个问题集既是课程内容，也是课程的习题集.这样的问题集一般包含有定义，公理，定理，命题等.学生的任务是解答问题集中的每个题目：如果题目是正确的命题，那就需要学生提供证明；如果题目是错误的命题，就要提供反例.

设计一个循序渐进，由浅入深，有助于学生积极参于丰富多样的数学活动，加强学生对课程内容的理解，探索更深的理论思想的系列问题是有效实施询问式教学的关键[10].通常一个有效的询问式教学的课程设计里包括以下几个要点：

(i) 它是基于学生已有的知识.

(ii) 它是循序渐进，由浅入深，从特殊上升到一般的过程.

(iii) 它在该课程中对学生有明确的期望和要求.

(iv) 它具有为学生之间的讨论和互助的一个框架.

(v) 它具有一个对课程的评估的机制.

为了了解课程问题集设计的思路，下面我们列出部分题目，从中可以看出问题集的相当一部分是在传统授课方式课堂里教师所讲授的定理和命题及其证明.但在以询问式为基础的教学中，学生们要自己独立解决这些问题.例如，在编写数学分析课程中函数序列问题时,首先需要列出相关的定义，之后给出一系列相关的问题.

参考问题集实例[13，4]

参考问题1

定义1设{fn}是定义在区间I上的函数序列.若有定义在I上的函数f，使得对于一切 x∈I, {fn(x)} 收敛于f(x)， 则称{fn(x)}在区间I上点收敛于f(x).

定义2设{fn} 是定义在区间I上的函数序列.若有定义在I上的函数f，对任给ε>0，存在 N， 使得当 n≥N 时，对于一切 x∈I有

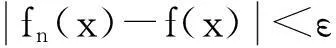
则称 {fn} 在区间 I 上一致收敛于 f(x).

问题1设{fn}是定义在区间I上的函数序列，{fn}在I上一致收敛于f，并且fn(n=1,2,3,…)在I上连续.证明f也在I上连续.

问题2(证明或驳斥)设{fn}是定义在[a,b]上的函数序列，fn(n=1,2,3,…)在 [a,b]上连续，并且在(a,b)上可微；如果{fn}在[a,b]上点收敛于f，则{fn}在 [a,b]上一致收敛于f.

问题3证明函数序列fn(x)=xn在[0,1]上点收敛但不一致收敛于函数

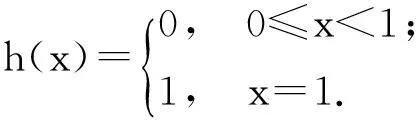
参考问题2

在给出极限点的定义后，即可给出类似以下的题目.

定义3设M是一个点集，p是一个点.如果每一个包含p的开区间都包含M中的一个不同于p的点，则称p是M的一个极限点.

问题4如果a,b是两个点，证明点a是[a,b]的一个极限点.

问题5如果M是一个仅包含3个点的集合.证明M没有极限点.

定义4设M是一个点集.如果存在一个点p使得x≤p, ∀x∈M，则称M是上有界.如果x≥p, ∀x∈M，则称M是下有界.如果M是上有界和下有界，则称M有界.

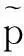
公理1如果M是非空点集并上有界，则M有上确界.

问题6如果M是非空点集并下有界，证明M有下确界.

问题7如果p1,p2,p3,… 是一个单调上升序列并上有界.证明序列p1,p2,p3,… 有极限点.

参考问题3

在线性代数课程中，在给出线性空间，线性子空间，线性相关等基本定义以后，就可以给出如下的问题：

问题8设M是线性空间L中的一个子集.证明M是一个子空间的充要条件是0∈M 和aP+bQ∈M,∀P,Q∈M，其中 a,b是数值.

问题9设 M={(x,y,z)∈R3:z=0}. 确定M是不是R3的一个子空间.

问题10设 B是线性空间L的一个子集.若0∈B，证明B线性相关.

此外，询问式教学法也可以用于象微积分(高等数学)一样的基础数学课程中[1]. 我们在下面给出一个微积分课程设计中的例子[8].

参考问题4

运用导数的定义，

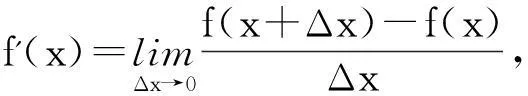
及导数的几何意义来推出函数图像的特性，例如，函数的递增，递减，极值等.

问题11作函数f(x)=x4-3x的图形并从中求出其递增和递减区间.这些区间的分界点的坐标是什么？

问题12求函数f(x)=x4-3x在点x=-3,-2,-1,0,1,2,3的导数值， 描述这些导数值的变化.判断它们与问题11的联系.

定义6若存在一个包含点c开区间I使得 ∀x∈I都有f(c)≥f(x)或f(c)≤f(x), 则称f(c) 为函数f(x)的一个极大或极小值.

定义7设函数f(x) 在点 c 有定义.若f'(c)=0 或f'(x) 在c 点不存在，则称点c为函数f(x) 的临界点.

定理2设函数值f(c)是f(x)的一个极大或极小值.则x=c是函数f(x) 的一个临界点.

问题14推出一个使用函数的导数来求此函数极大或极小值的步骤.

问题15(商业上的应用)设某产品的市场需求函数是

p=80-0.03x ,

这里x是市场对该产品的需求量，p是该产品的单位价； 此外，设生产x 数量产品的成本函数是

C=1000-10x-0.02x2.

试确定该产品的产量和单位价应是多少才能保证最大利润.

问题16试找出另外一个极值应用问题并利用导数来解决此问题.

除此之外，高速公路工程中的中心试验室也可以结合管理部门制定的各项管理制度，对工程各项数据进行综合分析，针对施工材料使用过程中遇到的问题，提出妥善的建议，保证工程中的施工材料得到充分利用。对于高速公路工程中的施工单位来讲，要根据中心试验室提出的意见，对原有的施工工艺进行有效改进，在保证高速公路工程整体施工质量的基础上，真正达到提高工程施工质量控制水平的目的。

3以询问式为基础教学法的课堂使用

3.1　教学大纲或课程规则的讨论

在美国大学里，通常在每学期的第一节课，任课教师会给修课学生课程综合信息即教学大纲(syllabus).这个大纲包括该课程目标，学习内容，教材信息，答疑时间，测验和考试安排和时间，作业要求等；当然也包括学生们最关心的一点，即课程成绩计算的详细说明.

运用以询问式为基础进行教学也同样要给出一个大纲.由于教学采用不同于传统授课方式，所以需要给出更详细的大纲.这个大纲除了包含通常课程信息以外，还需要说明该课程的规则：是否使用教科书，是否可以利用象图书馆一样的资源，是否可以上网来查询资料，同学之间的讨论是否允许等.因此，在学期第一节课中，需要比较细致地解释课程目标和大纲，课程的规则，及对学生的期望.使得修课学生对于使用以询问式为基础的教学有比较清楚的了解和心理上的准备.

通常在以询问式为基础教学课堂里，任课教师每次在开始一章新内容时传给学生一张签名表格.表格中包含当前需要解决的问题集列单.学生们将自愿选择并标明要讲解的题目，经准备后要上黑板给出该问题的解答或证明.如果有不只一个学生选择同一个题目，通常就由上黑板次数少的学生来进行讲解.教师一般尽量避免总是由程度比较好的学生来进行讲解.

当学生在课堂前面讲解问题时，其他学生的任务是对该学生给出的解答或证明进行评估和论证，提出问题和质疑.如讲解的学生对所提到的问题当时不能回答，也可以在下一节课给出答案.如果所讲解的问题解答或证明经过论证通过了，那么就可以以同样的方式由下一个学生来解决下一个题目.

如果课堂中对所讲解的问题无法取得共识，可以由全体学生一起来讨论和协商解决办法.有时讨论会产生新的问题，可以变成下次课所要讲解的问题.在没有学生上黑板讲解问题的情况下，也可以先施行分组讨论来研究解决问题的方式和策略.任课教师可根据不同的情况提供建议和引导，但尽量不要直接给出答案，以免学生产生依赖性.

3.2　作业问题部分(写作)

在使用以询问式为基础的教学中，还有一个重要组成部分——课程作业部分.在这部分中，学生独立写出问题的解答和证明.教师按照课程的进度，来收取作业.通常学生会有两种选择：

(i) 所提交的题目在课堂中讲解和讨论之前；

(ii) 所提交的题目在讲解和讨论之后.根据这两个选择，教师酌情地给予评估和分数.教师主要根据解答的准确性，语句和步骤等方面来评估作业.

课程分数分布参考实例

通常，在教学大纲里需要说明如何计算课程成绩及习题和测验占有的比重.下面是一个以询问式为基础的课程中成绩分布实例.

课程成绩分布： (i)作业部分25%； (ii)课堂讲解25%； (iii)期中考试20%； (iv)期末考试30%

另外我们给出一个在以询问式为基础的课程中对于学生讲解评估标准实例：

课堂讲解分数标准：

10. 完全正确

8-9. 证明正确，但在其过程中有少量的语句和步骤要修改.

6-7. 证明正确，但在过程中有语句和重要步骤要修改.

4-5. 不正确的证明，但能解释为何不正确或不知为何不正确

3分以下. 不着边际，题目没有进展，

3.3　使用以询问式为基础教学中可能出现的问题

在开始使用以询问式为基础进行教学时，由于课堂上的时间主要用于学生讲解问题和问题讨论，所以常常会感觉课程进度不够快.对于初次使用这个教学法的任课教师会面临“时间”问题——能否完成所有计划要学习的内容.因此任课教师在设计问题集时，就需要更详细地考虑哪些是课程核心内容而不可少的.哪些定理，引理和命题又是至关重要的，进而将这些部分编入在问题集里，以保持课程的完整性.

有时候任课教师会因为时间因素压力下想加快进度而给出问题的提示，这是应该避免的.因为这样做会使学生产生对教师的依赖性，削弱他们解决问题的自信心.这是违背以询问式为基础进行教学宗旨的：即培养学生独立解决问题的能力和信心.

另外，许多学生在第一次修以询问式为教学的课程时，开始会感到与授课方式的反差，产生困惑或不适应.因此在学期第一节课上，对于这个教学法，特别是其目的要详细说明，来帮助学生理解这个教学方法和该课程的实施规则.使学生认识到通过这种教学方式，由于学生自己在从事和参与发现，创造，解决问题的活动，他们独立思考，创造，批判式思维和清晰准确的表达等方面的能力得到培养和加强，对课程内容的理解会更深，从而提高在课程中学习的积极性和主动性.实践证明大多数在以询问式为基础的教学中的学生是喜欢这种方法的.

4结论

从上面对以询问式为基础的教学法的介绍和讨论中，可以看出此方法强调培养学生的独立思考，创造，批判式思维和清晰准确的表达等方面的能力.因此在美国大学里，越来越多的数学课程已使用此方法进行教学.特别是近年来，由美国教育发展基金(Educational Advancement Foundation)资助在以芝加哥大学在内的四所著名大学建立以询问式为基础教学法中心和成立以询问式为基础教学研究院(www.inquirybasedlearning.org)，来对这个教学法进行研究，推广和教师培训; 此外美国数学协会和教育发展基金还定期举办一年一度的以询问式为基础的教学法学术年会.这无疑促使当今使用以询问式为基础教学成为一个“新运动”.

近年来也有不少对以询问式为基础教学效果的研究.数据显示这个教学方法的效果是令人鼓舞的.例如，由科罗拉多大学拉森教授(Sandra Laursen)的团队对一百多门使用以询问式为基础进行教学的课程进行了评估和研究[11]，研究发现通过这样的课程，学生的学习效果相对于传统讲授方式相比有较大的进步.(详细参见http:∥www.colorado.edu/eer/research/steminquiry.html)

另外从教学理论上询问式教学法可以说是基于以下的三个原理[5]：

(i) 通过询问式的学习过程，学生对于知识的理解和记忆都明显优于授课老师直接传授方式教学.

(ii) 如果要讲授一部分课程内容，这样会促使讲员对于该内容掌握得就比较彻底.

(iii) 有效的写作和清晰的思路是紧密地联系起来的.

由上述原理可以看出这个教学方法不仅仅是适用于数学教学，它也可以应用于其它的学科.因此当今在美国大学里不少数学以外的课程也采用此方法进行教学.

随着以询问式的教学法从早期严格的摩尔方法扩展到修改式的摩尔方法，这种教学方式覆盖了许多当今常用的教学模式，例如，以学生为中心的模式，以解题为基础的模式，发现式或互助模式.询问式教学法已不仅仅用于在科学技术学科教学中，不仅仅局限在处理交叉学科问题及实际应用问题中. 这个方法在不同的场合以不同的形式已有得到广泛的使用. 近年来，如何用询问式教学法来设计其它教学模式，比如翻转课堂式[6]，同行引导或同行辅助式[7，12]，远程教育[17]，网络教育[15]，和其它计算机辅助教育[3]已有大量的研究. 询问式教学法更广更深的影响还有待去发现和进一步的探讨.

[参考文献]

[1]Briggs, Karen S, Bailey, Brad and Cooper, Thomas E. Doceamus: Is Moore Better (in Precalculus)?[J]. Notices of the AMS, 2011, 58 (07): 963-965.

[2]Chalice D R. How to teach a class by the modified Moore method [J]. American Mathematical Monthly, 1995, 102(4): 317-321.

[3]Chang K-E, Sung Y-T. & Lee C-L. Web-based collaborative inquiry learning [J]. Journal of Computer Assisted Learning, 2003, 19:56-69.

[4]Clark, David M. Linear Algebra [J]. Journal of Inquiry-Based Learning, 2008, 10: 1-31.

[5]Cohen, David W. A Modified Moore Method For Teaching Undergraduate Mathematics [J]. the American Mathematical Monthly, 1982, 89(7): 473-474,478-490.

[6]Devlin, Keith. The Greatest Math Teacher Ever [J]. Devlin’s Angle, 2015, February, http:∥devlinsangle.blogspot.com.

[7]Glassey J. Peer assisted instruction and VLE in enquiry based learning in chemical engineering [J], Experiment@ International Conference (exp.at'13), 2013, 2: 78,82, 18-20.

[8]Greene, Mairead and Shorter Paula. IBL Calculus: Concepts and Applications [M]. http:∥www.iblcalculus.com/, 2014.

[9]Halmos, Paul R. How to Teach, I want to be a Mathematician [M]. New York: Springer-Verlag: 1985: 253-265.

[10]Hmelo-Silver, Cindy E. Duncan, Ravit G and Chinn, Clark A. Scaffolding and Achievement in Problem-Based and Inquiry Learning: A Response to Kirschner, Sweller, and Clark [J]. EDUCATIONAL PSYCHOLOGIST, 2007, 42(2): 99-107.

[11]Laursen, Sandra, Hassi M. L.Student outcomes from inquiry-based college mathematics courses: Benefits of IBL for under-served groups [J]. Proceedings of the 14thAnnual Conference on Research in Undergraduate Mathematics Education, 2011, 3: 73-77.

[12]Morris D and Turnbull P. Using student nurses as teachers in inquiry-based learning [J]. J Adv Nurs. 2004, 45(2): 136-44.

[13]Neuberger, John W. Analysis [J]. Journal of Inquiry-Based Learning, 2009, 13: 1-16.

[14]Schinck, Amelie G. The Road to Present Day Inquiry-Based Learning [J]. 2014, December, http:∥www.inquirybasedlearning.org/?page=Why_Use_IBL

[15]Schrec, Vincent, Johnson Dan. Focus on Faculty: Promoting Interactive, Inquiry-based Environment in online education [J]. www.web.pdx.edu/~schrecv/focus_on_faculty.ppt, 2007:1-8.

[16]Warter-Perez, Nancy and Dong, Jianyu. Flipping the Classroom: How to Embed Inquiry and Design Projects into a Digital Engineering Lecture [J]. Proceedings of the 2012 ASEE PSW Section Conference Cal Poly - San Luis Obispo, 2012:1-17.

[17]Yoder, Maureen B. Inquiry based learning using the internet: Research, Resources, WebQuests [J]. 19thAnnual Conference on Distance Teaching and Learning, 2005:1-4.

[18]Zorn, Paul, RLM, EAF, MAA and IBL: Letters of Learning [J]. MAA Focus, 2012, 32, 4: 20-21.

Inquiry-Based Learning in College Mathematics in the US,

Its Past and Present

HANShu-PingSandie1,LUBin2，TUShu-Yi3，ZHONGJianyuan2

(1. Department of Mathematics，New York City College of Technology，Brooklyn, NY 11201, USA；

2. Department of Mathematics and Statistics, California State University Sacramento, Sacramento, CA 95819，USA；

3. Department of Mathematics, The University of Michigan-Flint, Flint, MI 48502, USA)

Abstract:Inquiry-based learning (IBL) is a well-known teaching method in college mathematics in the US. Its origin is from Dr. R. L. Moore of University of Texas, Austin. Compared to traditional lecture-based teaching, the IBL method makes students problem solvers and help students develop abilities in independent acquiring knowledge, critical and independent thinking, and creativity. Here in this paper we introduce IBL, its pedagogy and its classroom implementation. We also provide some examples of IBL course designs. In addition, we discuss some typical situations encountered when using IBL in a class.

Key words:Moore method; modified Moore method; inquiry-based learning

[中图分类号]G642.4

[文献标识码]C

[文章编号]1672-1454(2015)05-0053-07

[收稿日期]2014-09-10