基于H∞混合灵敏度方法的超声波电机调速控制

潘　鹏　 徐志科　 金　浩　 金　龙　 陈　爽　 黄　帆　 冷静雯

(东南大学电气工程学院, 南京 210096)

基于H∞混合灵敏度方法的超声波电机调速控制

潘鹏 徐志科 金浩 金龙 陈爽 黄帆 冷静雯

(东南大学电气工程学院, 南京 210096)

摘要:为提高行波型超声波电机转速跟踪的准确性和平稳性,改善因调频调速非线性带来的调速性能变化,将H∞混合灵敏度方法应用于转速控制器的设计．采用参数辨识法建立电机的频率转速模型,线性化得到电机的标称模型,将静态模型的非线性转化为标称模型的增益摄动,将动态模型的参数变化转化为标称模型的高阶未建模误差,把电机的转速模型表示为标称模型与误差模型和．根据模型误差界和调速性能指标,求取混合灵敏度加权函数,将控制器设计转化为标准的H∞优化问题,通过Matlab工具求解鲁棒控制器．仿真验证了转速闭环的稳定鲁棒性,使用数字信号处理芯片TMS320F28335在实际控制回路中实现该控制器,并测试电机调速性能．实验结果表明，鲁棒控制器应用于超声波电机调速系统可以取得良好的控制效果．

关键词:超声波电机;H∞鲁棒控制;混合灵敏度;转速控制

doi:10.3969/j.issn.1001-0505.2015.05.002

中图分类号:TM383

文献标志码:��码: A

文章编号:��号: 1001-0505(2015)05-0881-05

Abstract:For travelling wave type ultrasonic motors, in order to improve speed tracking’s accuracy and stability, and to enhance speed regulation performance owing to the nonlinearity of frequency modulation and speed regulation, the H∞mixed-sensitivity design method is adopted to design the speed controller.Based on parameter identification, the model of motor’s speed and frequency is established.It is linearized to get the motor’s nominal model, with the gain variation transformed from nonlinearity of the static model, the higher-order modeling error from the parametric variation of the dynamic model, and the sum of the nominal model and the error model from the motor’s speed model.According to model error bound and the speed regulation performance index, the mixable sensibility weighing function is solved, and the design of the speed controller is converted into standard H∞optimization problem. The robust controller is calculated by Matlab tools.The simulation results verify the control system’s robustness.The robust controller is also realized in the digital signal processor TMS320F28335 and the motor’s speed control performance is tested. The experimental results demonstrate that the speed control system applied to ultrasonic motor may provide a good control effect.

收稿日期:2015-03-07.

作者简介:��: 潘鹏(1983—),男,博士生;金龙(联系人),男,博士,教授,博士生导师, jinlong@seu.edu.cn．

基金项目:国家自然科学基金资助项目(51177014,51207021)．

Speed control of ultrasonic motor based on H∞

mixed-sensitivity design method

Pan Peng Xu Zhike Jin Hao Jin Long Chen Shuang Huang Fan Leng Jingwen

(School of Electrical Engineering, Southeast University, Nanjing 210096,China)

Key words: ultrasonic motor; H∞robust control; mixed sensitivity; speed control

引用本文: 潘鹏,徐志科,金浩,等.基于H∞混合灵敏度方法的超声波电机调速控制[J].东南大学学报:自然科学版,2015,45(5):881-885. [doi:10.3969/j.issn.1001-0505.2015.05.012]

近年来国内外学者在超声波电机位置伺服系统中应用鲁棒控制已取得了一些成果．Yoshida等[1]将H∞控制应用于超声波电机的位置控制．Nishimura等[2-3]采用李雅普诺夫目标函数的方式来提高系统的鲁棒性,并将该方法应用于超声波电机的位置控制．Nguyen等[4]把H∞方法用于直线超声波电机的位置控制.Sun等[5]使用鲁棒控制与PID相结合的方法对超声波电机的转速和位置进行控制．而鲁棒控制应用于超声波电机速度伺服控制方面的成果相对较少,其中Boukhnifer等[6]将H∞控制用于环形行波超声波电机转速控制中,把电机受到的扰动归结为定子表面行波和转矩的变化,并仿真验证了H∞控制策略的有效性.但是Boukhnifer等[6]采用了机理建模方式,使得电机转速模型比较复杂,实用性受到限制．相比之下,使用辨识法取得电机标称模型,把温度、摩擦和转矩扰动看作是参数的摄动,以闭环系统的混合灵敏度作为目标函数,设计鲁棒控制器的方法更加实用．

本文对直径60 mm行波超声波电机的调速模型进行辨识并给出模型误差范围,使用H∞混合灵敏度方法设计鲁棒控制器．使用基于DSP芯片的硬件平台实现该控制器,实验结果表明，H∞鲁棒控制器具有结构简单可靠、计算量小、容易实现的优点．

1超声波电机的转速模型

1.1　转速阶跃实验下的模型辨识

使用Hammerstein模型对转速模型进行描述[7]．通过阶跃调频调速实验测试电机转速的阶跃响应过程,记录此时电机频率和电机稳态转速的对应关系,获得电机的稳态转速模型．于39.5～43.5 kHz的频率范围内,在不同的转速工作点处,每隔500 Hz对电机进行阶跃调频测试,转速与频率的稳态关系如图1所示．

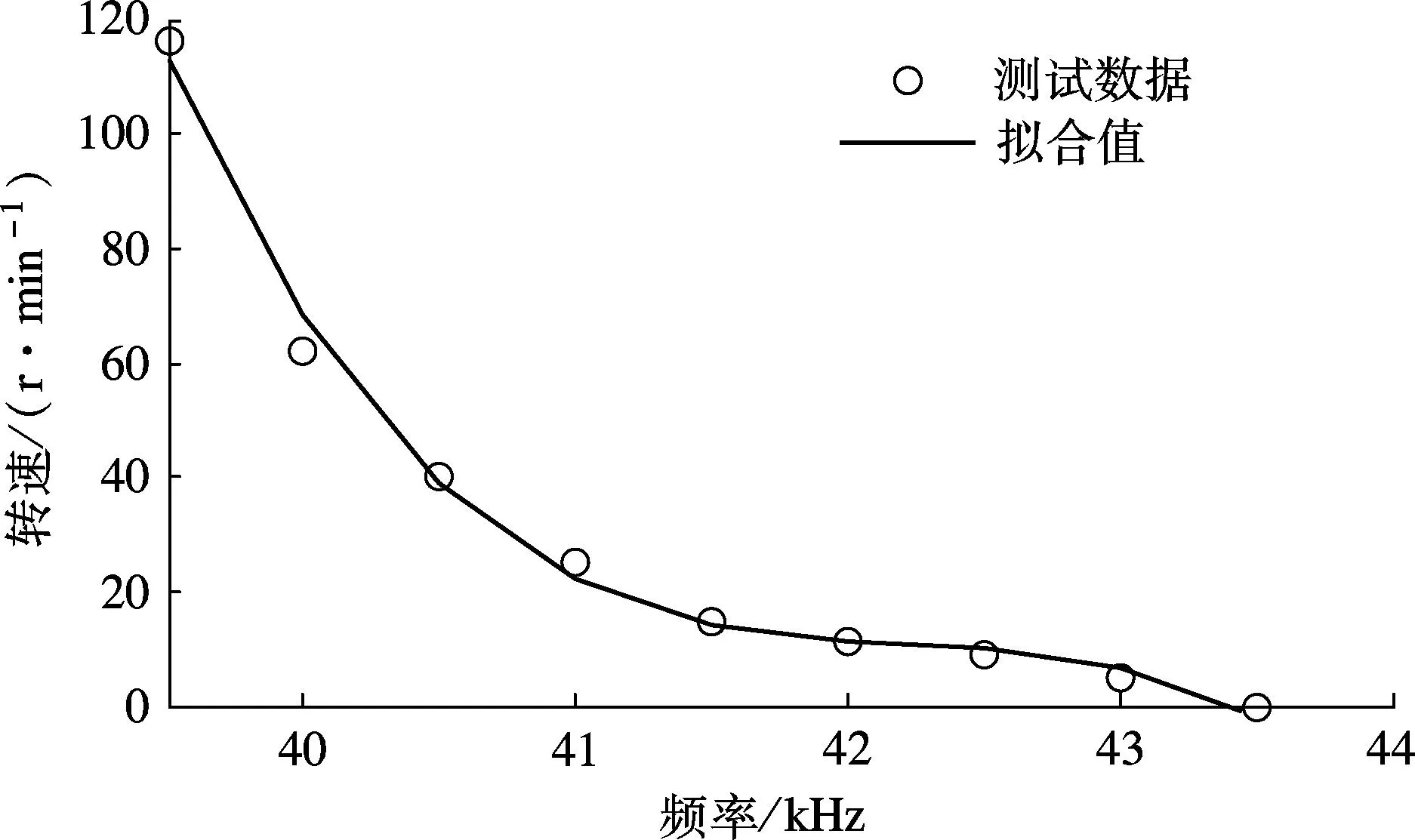
图1　超声波电机稳态转速模型

使用三次多项式拟合结果为

y(f)= 4.7(43.5-f)3-17.7(43.5-f)2-

24.3(43.5-f)-1.4

(1)

式中,f为电机的驱动频率,kHz;y(f)为稳态转速,r/min．令u=43.5-f,对电机的调频区间进行增量线性化,写成比例环节为

Δy=K0Δu

(2)

式中,K0为转速模型线性化后的标称增益．由图1可知,低速时增益较低,高速时增益较高．为取得固定参数控制器,在计算控制器时,将K0折中取值为K0=55．由固定K0取值带来的模型误差作为有界模型扰动,在模型误差中予以考虑．

通过记录电机阶跃调频响应的瞬态过程,使用参数估计的方法获得电机的瞬态响应模型．将所记录数据通过以下方式做归一计算:

(3)

式中,Y*(t)为归一化后的转速响应;y1(t)为频率阶跃后电机的实际转速响应;y0(∞),y1(∞)分别为频率阶跃前后电机的稳态转速．电机的瞬态响应过程归一化后如图2所示．

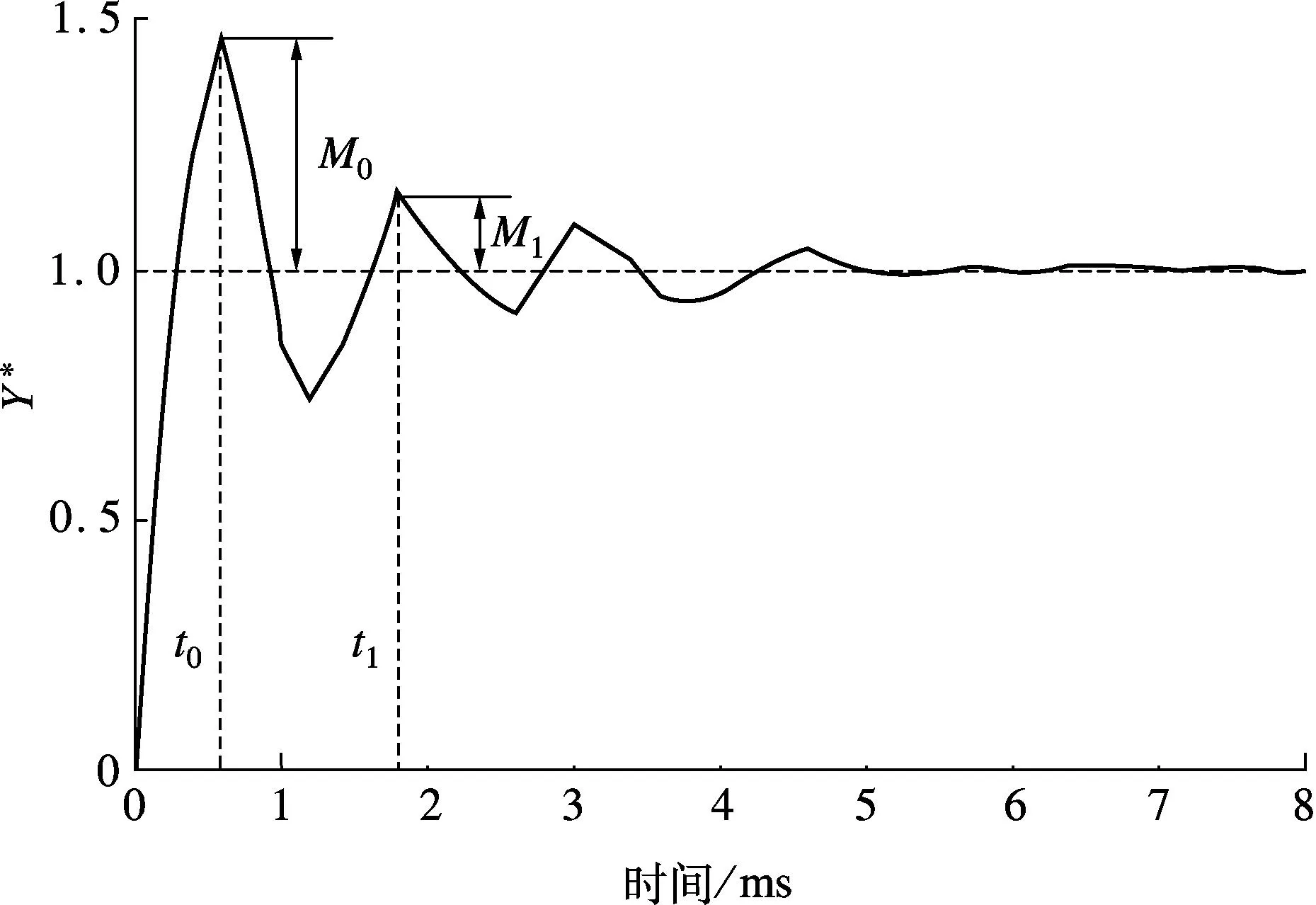
图2　归一化后超声波电机阶跃转速响应曲线

使用二阶惯性环节对转速瞬态模型做参数拟合,已知二阶惯性环节阶跃响应的峰值M0和峰值时间t0就可以求解其特征参数[7],其模型辨识结构为

(4)

式中,ωn为无阻尼振荡频率;ζ为阻尼比．

超声波电机动作响应快,但仍然存在延迟环节.对比阶跃试验输入频率阶跃时刻和电机转速响应时刻,获得电机的延迟时间为τ=0.5ms.因为系统延迟小于电机响应的振荡周期，因此为了不增加模型的阶数,建模时将延迟计入系统的建模误差中．

综上，电机的线性化标称模型为

(5)

其中,K0=55r/(min·kHz),ωn=5 318.53rad/s,ζ=0.18．

1.2　建模误差与模型摄动上界

由于模型辨识试验采用了基于线性二阶系统的参数估计,忽略了模型的非线性和高阶响应,使得标称模型和真实模型在系统增益和高频模型上存在一定的差异,在二阶系统的参数估计上也存在一定的摄动范围.

记电机的真实模型为P*(s),系统的模型误差为Pδ(s),两者与标称模型P0(s)的关系可以表述为

P*(s)=P0(s)+Pδ(s)

(6)

在电机的实际工作过程中,Pδ(s)受到工作频率、轴上负载、温升等多重因素影响,因此很难精确给出其值,但由于这些扰动通常都是有界的,故可以给出一个Pδ(s)变化的范围．电机在中低频段的建模较为准确,因此把真实模型表示为

(7)

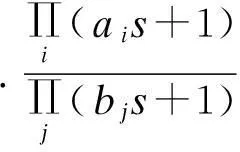
将式(7)代入式(6)，得

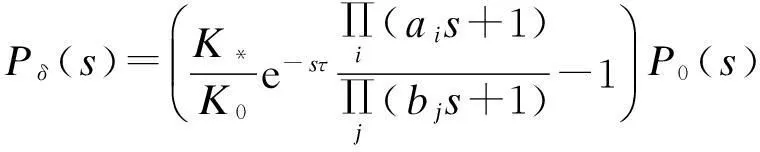
(8)

以辨识模型的自然频率为划分,误差界近似表示为

(9)

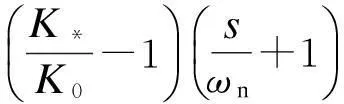
2基于混合灵敏度的H∞控制器设计

H∞最优控制理论的基本方法是寻求一个参数固定且自身在复平面右开平面解析的控制器K(s),使得对于存在有界摄动的被控对象P0(s),控制回路闭环稳定,且某特定的闭环性能指标的H∞范数取得极小值[8]．基于混合灵敏度S/T(T为补灵敏度，S为灵敏度)的H∞控制器设计方法折中考虑了系统摄动带来的系统稳定和系统性能问题,对于结构不确定性系统是行之有效的设计方法．为了借助计算机求解控制器,需要把混合灵敏度问题转化为标准的H∞优化问题,因此S/T加权函数的选择成为影响控制器的重要因素．S/T加权函数WT(s)和WS(s)的选取依据是系统的稳定性要求和性能指标要求．参数摄动模型的超声波电机转速反馈闭环控制结构如图3所示．图中,d表示系统受到的外来扰动．

图3　电机在乘性摄动下转速控制系统框图

2.1　系统的稳定鲁棒性约束

如果控制器K(s)能够使系统满足内稳定,则系统输入输出稳定．根据小增益原理[9],系统内稳定的条件为系统的环路增益模值小于1．

因此电机模型存在有界扰动时,其系统稳定性约束条件可以写成

(10)

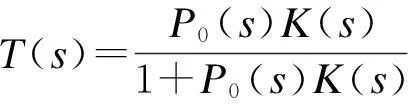
(11)

2.2　系统的性能鲁棒性约束

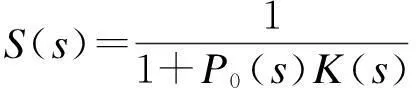
在H∞方法中通过对加权函数的设置给出灵敏度指标,反之可以通过期望的灵敏度指标推算灵敏度加权函数．记灵敏度加权函数为WS(s),H∞方法的计算规则可以表示为

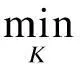
(12)

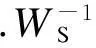
1) 快速性．在频域设计中提高系统的带宽可以有效减小系统的调节时间．超声波电机具有很高的响应速度,考虑到实际控制器的采样计算速度限制,选取带宽为500rad/s．

2) 准确性．为了满足调速系统的渐进跟踪和扰动抑制的性能,要求灵敏度函数的零频幅值趋近于0,因此在低频段灵敏度应具有较大的衰减幅度,但这会引起稳定裕度的降低,因此折中选取S(s)在低频段幅值衰减-40dB．

综上选取系统的灵敏度指标为

(13)

2.3　基于Matlab的H∞控制器的求解

根据以上分析,控制器的约束方程为

(14)

求解方程(14)，可以使得控制器同时满足稳定条件和性能条件．使用Matlab中的hinfsyn函数求解控制器，得

(15)

将控制器代入灵敏度和补灵敏度表达式,并计算得到幅频特性如图4所示．

图4　标称模型下灵敏度与补灵敏度幅频特性

为了将计算所得控制器应用于实际控制系统中,需要对控制器进行离散化.为了能够反映电机的动态特性,采样周期取0.1ms．在Matlab中采用0阶保持近似算法,控制器进行离散化得

K(z)=

(16)

略去式(16)中的小分量,得实际控制器为

(17)

若再进一步简化控制器可以得到

(18)

可以发现，式(18)与增量式PI控制器在形式上只相差一个延迟环节,其前半部分与增量式PI控制器具有相同的形式,换算为PI参数为kp=0.000 835 5, ki=12.345．

3超声波电机转速跟踪实验

实验平台硬件由TMS320F28335芯片、推挽驱动电路和光电编码器(10000线)构成,电机为直径60mm环形行波型超声波电机．

控制电机转速由20r/min分别向60和100r/min做转速阶跃,阶跃时刻为0.03s,对比鲁棒控制器和PI控制器作用下电机的阶跃响应．其中鲁棒控制器参数为模型计算获取,PI控制器参数通过工程整定方法[10]在60r/min的阶跃实验中确定,其中kp=0.003, ki=20．

图5(a)显示在2种控制器作用下目标转速60 r/min的转速阶跃响应过程,2种控制器都可以稳定、准确地达到目标转速．经过鲁棒控制器校正后系统的带宽变小,导致转速响应过程的调节时间为25 ms,而同时由于电机在此频率段的实际转速模型增益小于电机标称模型的增益,也使得电机转速调整过程较平缓.与PI控制器相比,在调整快速性上,PI控制器具有优势,经PI控制器校正后的系统仍然运行在欠阻尼状态,因此具有较快的响应速度．

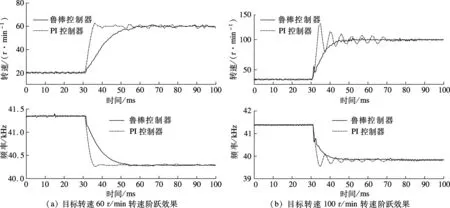
图5　2种目标转速下的转速阶跃效果

图5(b)显示了在2种控制器作用下电机由20 r/min向100 r/min转速阶跃的过程,实验表明，2种控制器都可以稳定、准确地到达目标转速.由于电机在100 r/min附近时,其真实模型的转速增益值较大,调速过程变快,鲁棒控制器作用下的转速调整时间约为15 ms,相对应的PI控制器达到转速峰值的时间也缩短.说明相同的控制器作用下,电机具有较大转速增益时,其转速上升时间减小,但PI控制器的调整效果的平稳性也随着转速增益的增大而变差．相比60 r/min阶跃时,PI控制器作用下转速超调和调节时间都变大,因此在转速平稳性上鲁棒控制器具有优势,系统不存在超调,调速过程具有良好的平稳性．

4结语

本文将超声波电机标称模型的模型误差和转速系统性能指标分别转化为补灵敏度加权函数和灵敏度加权函数,通过Matlab函数求解混合灵敏度约束下的最优控制器参数．使用TMS320F28335芯片实现了控制器在实际转速控制系统中的应用,降阶简化后的鲁棒控制器和PI控制器具有相似的结构形式,说明简化后的鲁棒控制器和PI控制具有相似的控制效果．

实验表明,基于混合灵敏度的鲁棒控制器能够在超声波转速跟踪控制中起到较好的效果,虽不能保证在每种工作情况下性能最优,但能确保在模型摄动情况下调速过程平稳可靠．

参考文献(References)

[1]Yoshida T, Senjyu T, Nakamura M, et al. Position control of ultrasonic motors using two-control inputs H∞controller [J].ElectricPowerComponentsandSystems, 2007, 35(7):741-755.

[2]Nishimura Y, Tanaka K, Wakasa Y, et al. Robust angle regulation for ultrasonic motor using CLF-based controller [C]//37thAnnualConferenceonIEEEIndustrialElectronicsSociety. Melbourne, Australia, 2011: 716-721.

[3]Odomari S, Darba A, Uchida K, et al. Robust position control of ultrasonic motor considering dead-zone [C]//InternationalConferenceonElectricalMachinesandSystems. Incheon, Korea,2010:684-688.

[4]Nguyen M H, Tan K K, Liang W, et al. Robust precision positioning control on linear ultrasonic motor [C]//IEEE/ASMEInternationalConferenceonAdvancedIntelligentMechatronics. Wollongong, Australia, 2013:170-175.

[5]Sun Z, Li H, Huang W. Control of multiple ultrasonic motors with robust parameter design [C]//IEEEUltrasonicsSymposium. Beijing, China, 2008:1827-1830.

[6]Boukhnifer M, Chaibet A, Larouci C. A robust speed control architecture for ultrasonic motor[C] //35thAnnualConferenceonIEEEIndustrialElectronics. Porto, Portuguesa,2009:1409-1414.

[7]王心坚.行波超声波电机伺服控制特性理论与实践研究[D]. 南京: 东南大学电气工程学院, 2007.

[8]张显库,贾欣乐,王兴成,等.H∞鲁棒控制理论发展的十年回顾 [J].控制与决策,1999(4):2-9.

Zhang Xianku, Jia Xinle,Wang Xingcheng, et al. Review of the development of H∞robust control theory in past decade[J].ControlandDecision, 1999(4):2-9. (in Chinese)

[9]韩智玲, 唐蕾, 李伟. 交流传动电力机车车网电压不稳定的原因分析与解决[J]. 铁道学报, 2011, 33(10):25-28.

Han Zhiling,Tang Lei, Li Wei. Causal analysis and resolution of the voltage Instability between AC drive electric locomotive and power supply network [J].JournaloftheChinaRailwaySociety, 2011, 33(10):25-28. (in Chinese)

[10]段力学. PID参数整定方法分类与概述[J]. 现代计算机月刊, 2012 (5):23-26.

Duan Lixue.Category and summarization of PID parameters tuning methods [J].ModemComputer, 2012(5):23-26. (in Chinese)