Ⅱ型地下连续墙接头力学性能的简易计算方法

金晓飞　 张玉良　 梁书亭　 朱筱俊

(1东南大学土木工程学院,南京210096)(2东南大学建筑设计研究院有限公司,南京210096)

Ⅱ型地下连续墙接头力学性能的简易计算方法

金晓飞1张玉良1梁书亭1朱筱俊2

(1东南大学土木工程学院,南京210096)(2东南大学建筑设计研究院有限公司,南京210096)

摘要:运用等值梁法对Ⅱ型地下连续墙接头在施工阶段的受力和变形进行理论分析,并给出了Ⅱ型接头施工过程中内力和变形的计算公式.利用得到的计算方法,计算实际工程中Ⅱ型地下连续墙接头的内力及变形,并通过建立三维非线性有限元模型验证了该计算方法的正确性,分析了上端2种不同约束形式对接头力学性能的影响.分析表明，上端刚接约束比铰接约束接头的内力分布均匀,最大变形小.该方法可为以后该类接头初步预测及检查设计提供参考.

关键词:Ⅱ型接头;力学性能分析;简易计算方法;施工过程模拟

doi:10.3969/j.issn.1001-0505.2015.05.002

中图分类号:TU473

文献标志码:��码: A

文章编号:��号: 1001-0505(2015)05-0929-06

Abstract:By using equivalent beam method, the force and deformation of a type Ⅱ joint of diaphram wall in the construction stage are theoretically analyzed, and a simplified calculation method of the forces and deformation of a type Ⅱ joint is proposed based on the analysis of the construction sequences of joint. Using the calculation method, the force and deformation of a type Ⅱ joint in the practical project are calculated, and the proposed method is verified through the three-dimensional nonlinear finite element method. Then, the effect of two kinds of tupper end constraints on the joint mechanical properties is analyzed. The results show that the rigid constraint can improve the stress state of joint, and make the maximum deformation of joint smaller than simple support. The proposed method can be used to preliminarily predict and check the final results of design.

收稿日期:2015-02-03.

作者简介:��: 金晓飞(1985—)，男，博士生;梁书亭(联系人)，男，博士，教授，博士生导师，stliang@seu.edu.cn.

基金项目:国家自然科学基金资助项目(51208181)、“十二五”国家科技支撑计划资助项目(2011BAJ10B08)、江苏省“333高层次人才工程”资助项目(1105000207).

Simplified calculation method for mechanical performance of

type Ⅱ joint of diaphragm wall

Jin Xiaofei1Zhang Yuliang1Liang Shuting1Zhu Xiaojun2

(1School of Civil Engineering, Southeast University, Nanjing 210096, China)

(2Architects and Engineers CO., LTD, Southeast University, Nanjing 210096, China)

Key words: type Ⅱ joint; analysis of mechanical properties; simplified calculation method; construction process simulation

引用本文: 金晓飞，张玉良,梁书亭,等.Ⅱ型地下连续墙接头力学性能的简易计算方法[J].东南大学学报:自然科学版,2015,45(5):929-934. [doi:10.3969/j.issn.1001-0505.2015.05.019]

随着城市化进程的加速和高层建筑的增多,基坑工程设计与实践变得越趋复杂,基坑开挖问题也越来越成为岩土工程领域中的研究热点.到目前为止,地下连续墙被用作围护结构甚至是“两墙合一”结构在深基坑施工中所占的比例越来越大,为了保证墙体整体性能和抗渗漏性能,选择恰当的地下连续墙接头是地下连续墙工程中应考虑的关键问题之一,研究表明接头的设计方法和施工工艺对整个地下连续墙工程的质量影响很大[1-5].

近年来,国内外研究人员对地下连续墙接头形式进行了研发及实践,为各种地质条件下的连续墙提供了有效的接头形式[6].地下连续墙接头按其受力特点主要分为柔性和刚性2种接头形式.其中,柔性接头与地下连续墙之间无可靠刚性连接,此类接头的应力传递效果差,受力后易变形,且基本没有抗剪和抗弯能力;刚性接头传递应力能力较强,其抗剪和抗弯能力较好,且渗水路径较长，止水效果较好[7].近年来,在我国的地下连续墙工程中工字钢接头是一种较常用的接头形式,这种接头具有防渗漏性能好、连接可靠、抗剪和抗弯强度高等优点.但是在复杂地质条件下,端部焊接工字钢接头的钢筋笼越长,其在下放过程中越容易出现卡笼现象,地下连续墙质量受到施工及吊装的影响也越大,且极易引起严重的质量和安全事故.

鉴于以上问题,南京地区在工程实践中以工字钢接头为基础提出了新型Ⅱ型地下连续墙接头,此接头在翼缘之间设置两道腹板,中间浇注混凝土,并且先于槽段施工,Ⅱ型接头和地下连续墙槽段可以实现流水作业,从而提高施工效率;同时地下连续墙的槽段可以全部按照闭合幅施工.该接头不仅具有工字钢接头的优点,而且在一定程度上克服了工字钢接头中钢筋笼卡笼、垂直度难以保证等施工难题.

目前对Ⅱ型地下连续墙接头的研究情况未见报道,其在施工过程中的力学性能还没有经过系统研究,实际工程中主要是根据经验选用.本文主要对Ⅱ型地下连续墙接头在地下连续墙施工阶段的受力和变形进行理论分析并给出相应的设计公式,通过一个实际工程中接头力学性能的数值解验证了该计算方法的正确性,并通过分析上端2种约束形式对接头力学性能的影响,给出了接头上端约束形式选用的建议.

1Ⅱ型地下连续墙接头的力学性能

1.1　Ⅱ型接头内力分析

Ⅱ型地下连续墙接头截面如图1所示[8].Ⅱ型接头在施工过程中,受到泥浆或者混凝土侧压力的作用始终与土体处于紧密接触状态,本文依据等值梁法及极限平衡理论对Ⅱ型接头在地下连续墙施工过程中的受力性能进行分析,分析中假定接头抗力为土极限状态下的土压力.

Ⅱ型接头是在超深地下连续墙施工中提出的,如图2(a)所示,底部嵌岩,桩身长度Z往往要比嵌固部分长度Z0长很多.该接头先于地下连续墙槽段施工,接头施工完成后,回填两侧填土至导墙顶.地下连续墙槽段施工时,在泥浆护壁下进行接头一侧槽段的施工,考虑到接头同时受到泥浆或混凝土侧压力和土压力的共同作用,且接头受到端部约束.综上分析,对开挖槽段底部以上部分隔离体按图2(b)、(c)模型进行力学分析.分析时假定隔离体上、下端水平位移为0,下端约束条件近似视为刚接约束.在分析中,所述接头均指隔离体.

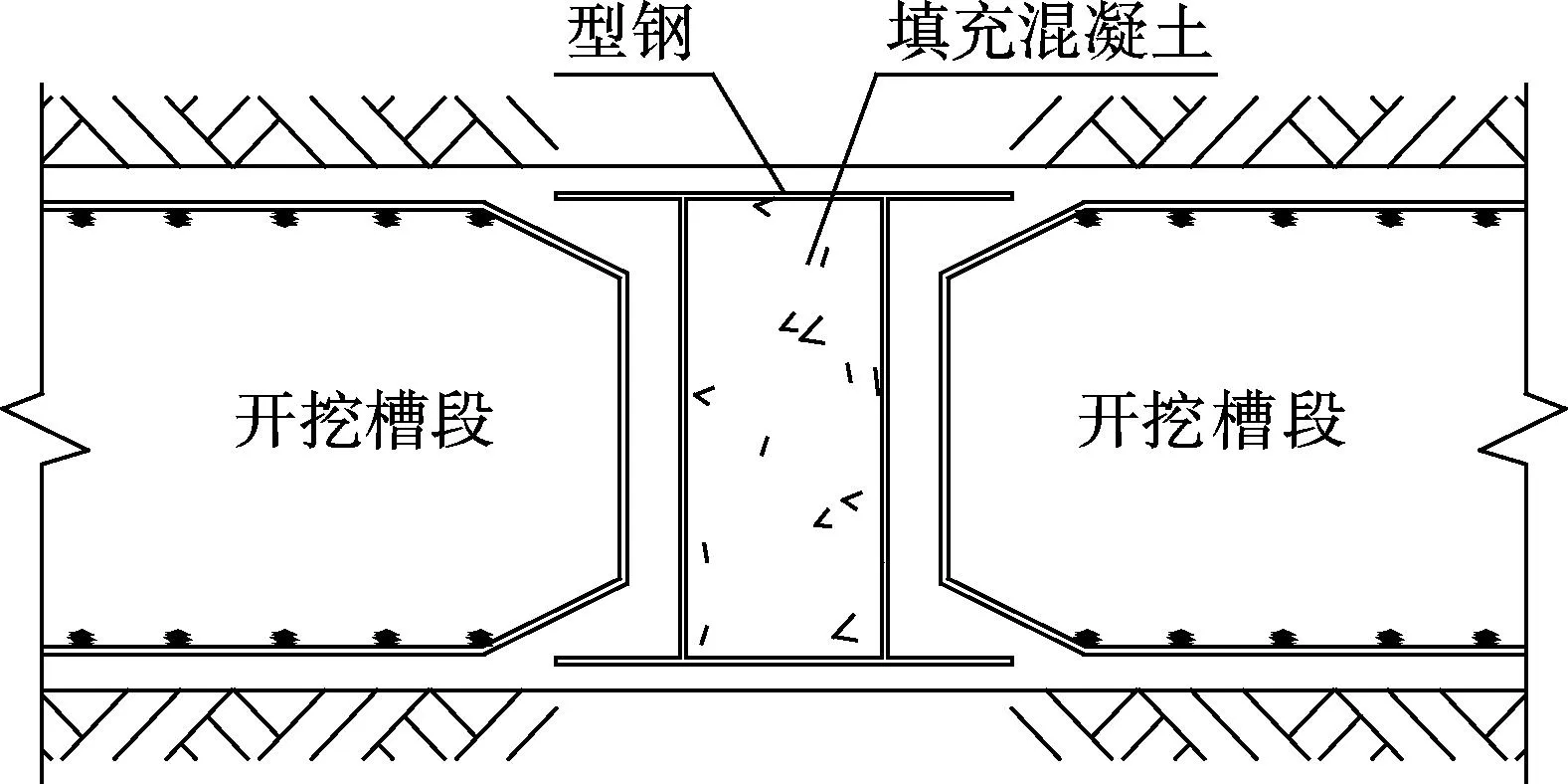
(a) 连续墙

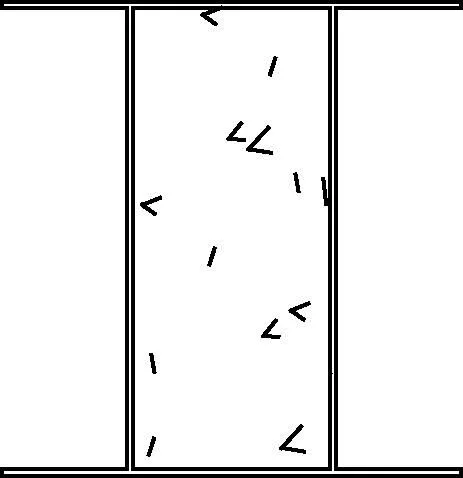
(b) Ⅱ型接头

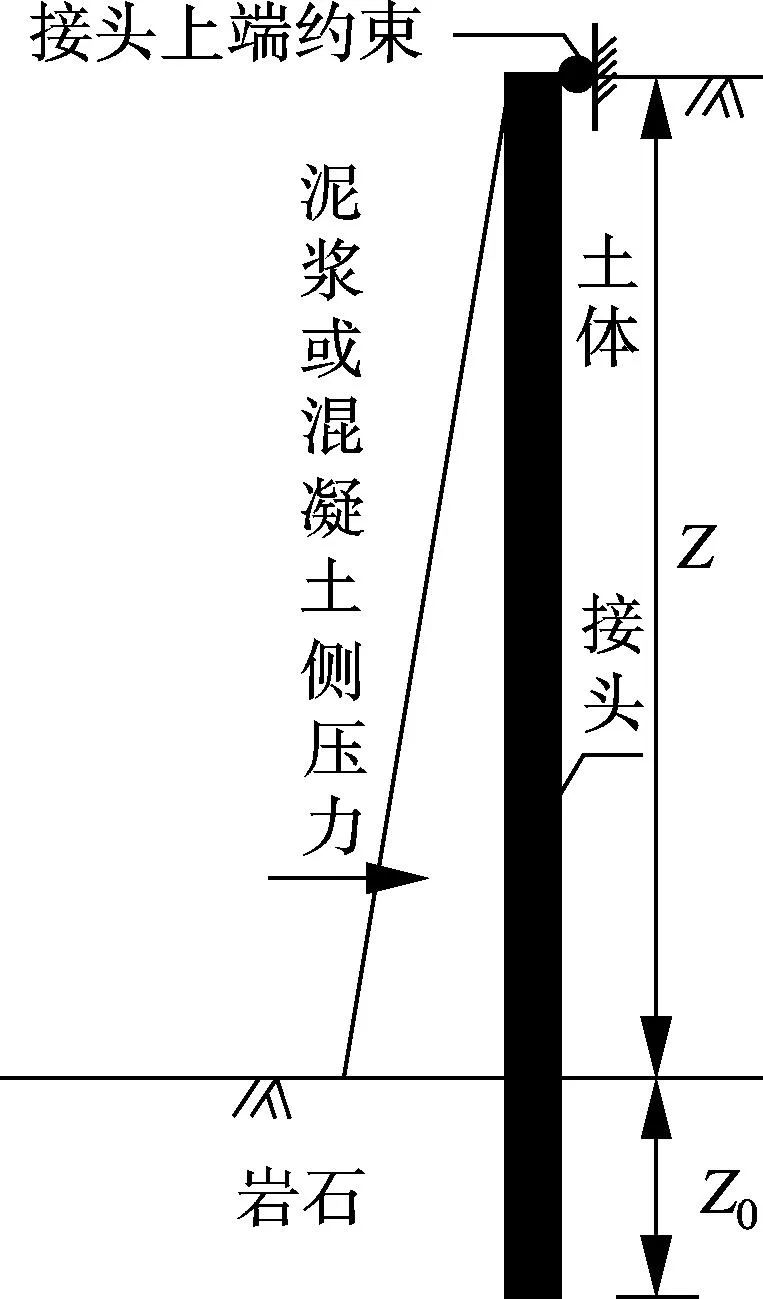
(a) 结构分析

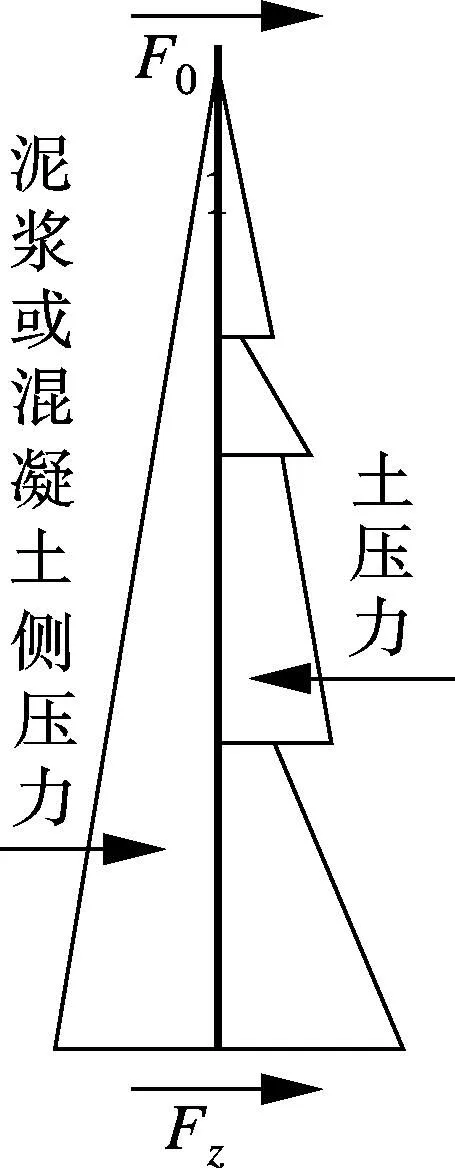
(b) 接头水平向受力

(c) 接头力学计算简图

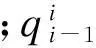
受力分析时,接头底部按刚接约束考虑,上端的约束形式可以根据接头上端固定于导墙的情况分为以下2种约束形式:① 铰接约束.此时接头上端与导墙约束部分仅能发生转动而无位移,可看作铰接约束.② 刚接约束.此时接头上端与导墙约束部分不但不能发生位移,且其转动也受到限制,故可看作刚接约束.刚接约束可以通过增设Ⅱ型接头翼缘内部多排螺栓加强其与导墙连接及加强接头露出导墙部位约束来实现.

根据接头上部不同约束形式,可以将接头约束形式分为上端铰接、下端刚接约束和上、下端均为刚接约束2种.接头内力随深度的表达式为

i≥2,z≥zi-1

(1)

(2)

根据式(1)、(2)可知,若要了解其内力分布情况,则需要已知F0,M0.接头上端的2种约束形式具体分析情况如下.

1) 上端铰接约束形式

以接头z位置上部隔离体作为参考,根据力法原理有

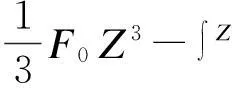
(3)

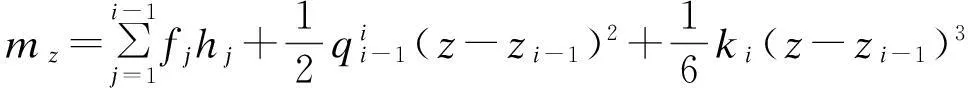
(4)

通过以上分析,得到深度z处接头弯矩Mz和剪力FQ,z分别为

(5)

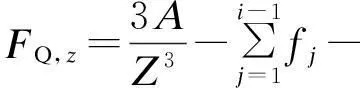
(6)

2)上端刚接约束形式

根据力法原理有

(7)

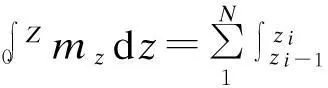
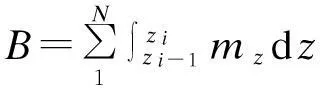
(8)

(9)

则上端为刚接约束时,深度z处接头弯矩Mz和剪力FQ,z分别为

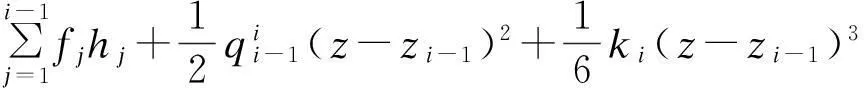
(10)

(11)

1.2　Ⅱ型接头变形分析

接头挠度可以根据下式得出,其中挠度以向开挖槽段方向变形为正：

(12)

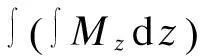
(13)

结合式(12),接头挠度的计算公式为

(14)

2有限单元法分析

2.1　工程概况

图3是南京河西地区某基坑工程项目平面示意图.该基坑南北向长130 m,东西向长140 m,呈不规则方形,周长545 m,采用钻孔桩筏基础,基坑面积18 220 m2;基坑围护结构在南、西、北侧采用1 m厚“两墙合一”地下连续墙,地下连续墙分4种类型的槽段,共63幅,地下连续墙平均深度为60 m.槽段之间采用新型Ⅱ型地下连续墙接头连接.

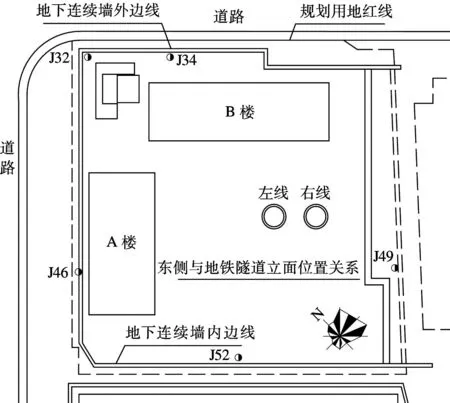
图3　基坑平面示意图

2.2　有限元分析模型

本文选择一幅地下连续墙槽段进行模拟研究.模型尺寸为:土体长度l=100 m,宽度b=50 m,深度h=100 m;开挖槽段宽度为1 m,深度为60 m,接头净距为6 m,接头尺寸见图4(a),模型沿槽段宽度方向对称建模;模型中单元类型均为C3D8六面体单元.接头与土体间通过接触连接,其正应力模型选用硬接触模型,切应力模型选用罚函数接触模型,摩擦系数统一取为0.3.计算模型网格划分如图4所示,共114 568个单元网格,136 029个单元节点. 土体本构模型选用经典的 Mohr-Coulomb

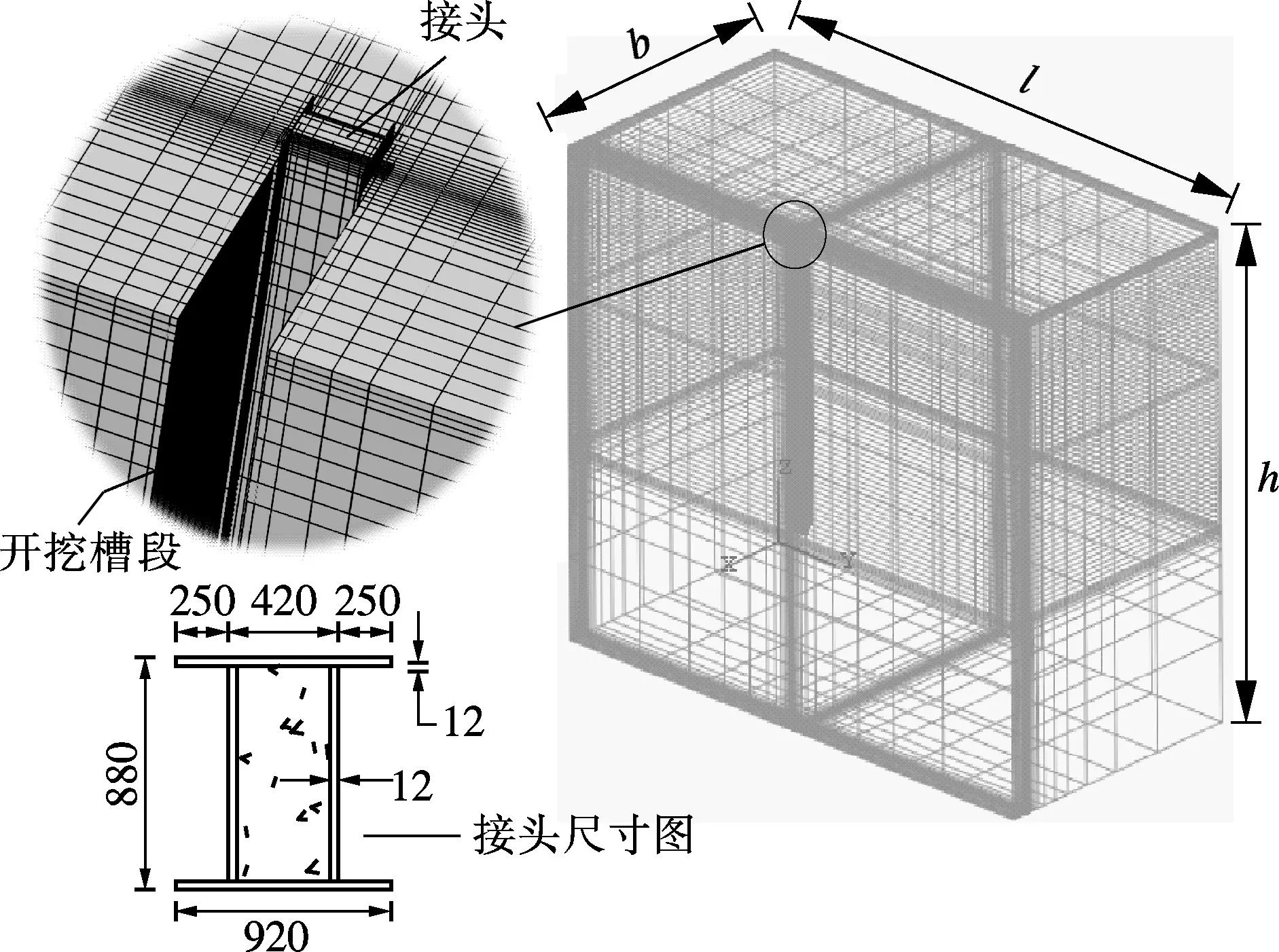
(a) 整体网格划分(单位：mm)　　　　(b) 竖向网格划分

理想弹塑性模型,接头由Q235型钢和强度等级为C40的混凝土制成.钢材密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.23,运用双折线模型;混凝土密度为2 500 kg/m3,弹性模量为32.5 GPa,泊松比为0.2,运用线弹性模型.

模型中的岩土力学参数见表1.

表1　岩土力学参数

2.3　地下连续墙接头施工模拟

ABAQUS可以模拟多种施工工况,但对于一些施工工序,如排渣、清孔等仍无法实现.本文主要分析接头在槽段开挖过程中的受力性能.根据文献[9-13]对地下连续墙槽段开挖施工过程的分析,考虑到槽段开挖阶段对地下连续墙接头力学性能的影响是研究的重点,本文研究的接头施工工序为:① 接头施工;② 泥浆护壁下的槽段开挖.开挖过程中将泥浆压力简化为静水压力.泥浆压力σh=γsz,其中,γs(10.7 kN/m3)为泥浆重度.

3数据分析与讨论

根据分析,将地下连续墙接头上端铰接与上端刚接情况下内力和变形理论计算值与有限元模拟值进行对比,结果如图5～图7所示.用式(5)、(6)、(10)、(11)、(14)计算接头的内力和变形值时,为了方便计算可以根据刚度等效原则将接头截面形状简化为矩形或圆形.

如图5(a)所示,上端铰接接头弯矩的计算值与模拟值均呈先逐渐增大后逐渐减小的趋势,其中模拟值略大于计算值,反弯点深度计算值(-46.5 m)与模拟值(-49.5 m)比较接近;如图5(b)所示,上端刚接接头顶部弯矩为负值,此时,反弯点深度计算值与模拟值分别为-48.0和-50.0 m,相差4%.弯矩最大值及反弯点深度随接头上部施加转动约束呈现下移趋势.以计算值为例,上端铰接和上端刚接的弯矩最大值深度及反弯点对应的深度分别为-26.0，-46.5m(铰接)和-32.0，-48.0 m(刚接).

如图6(a)、(b)所示,上端铰接、上端刚接2种约束形式的接头剪力的绝对值都呈由大变小再由小变大的趋势,剪力最大处均处于接头的底端.上端铰接的接头底端剪力计算值和模拟值分别为-388.8和-375.8 kN;上端刚接的接头底端剪力计算值和模拟值分别为-340.2和-333.1 kN.2种算法算得的接头不同约束形式的剪力值非常接近,上端铰接接头2种算法相差3.45%,上端刚接接头2种算法相差2.1%.

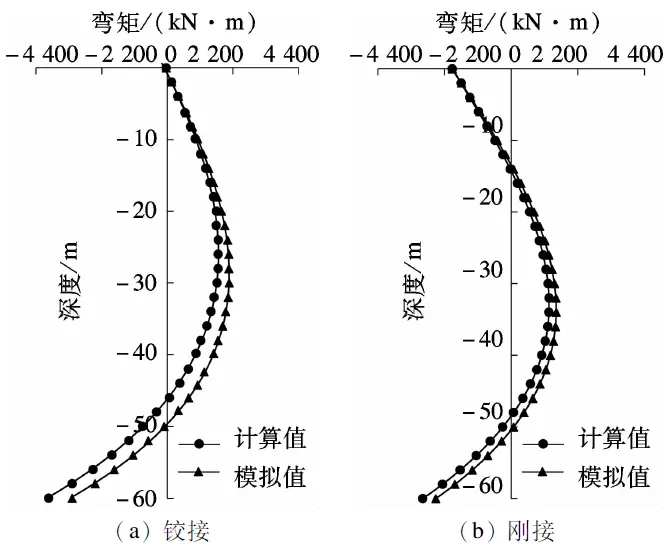
图5　接头弯矩对比图

图6　接头剪力对比图

如图7(a)、(b)所示,由2种方法计算得到的接头挠度变形曲线也较一致,其中接头上端铰接约束时,最大挠度深度计算值和模拟值分别为-34.0和-30.9 m,最大挠度位置偏差为9.1%,2种方法算得的最大挠度值分别为2.07和2.36 mm,最大挠度值偏差为12.3%;接头上端刚接约束时,最大挠度深度计算值和模拟值分别为-38和-36.2 m,最大挠度位置偏差为4.74%,2种方法算得的最大挠度值分别为1.81和2.08 mm,最大挠度值偏差为12.98%.

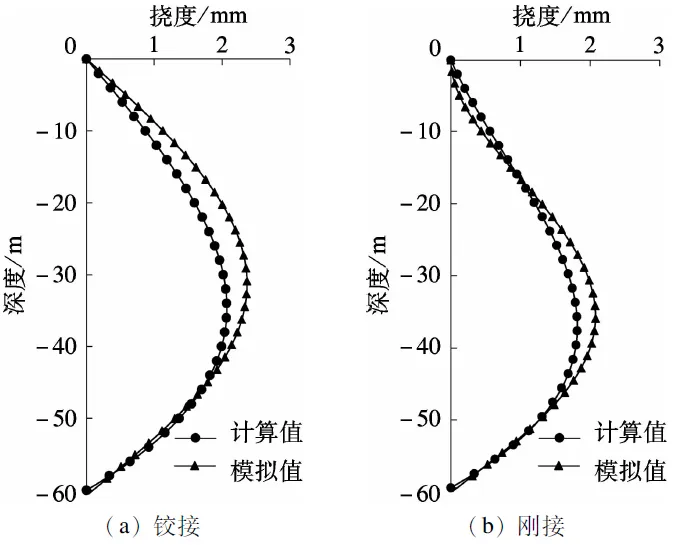
图7　接头变形对比图

由图5～图7中可以看出,计算值与模拟值内力及变形分布规律吻合较好,模拟值略大于计算值,这是因为运用有限单元法对接头的力学性能进行计算时,模型参数的选取及网格的划分都会对分析结果产生一定的影响,所以模拟值与计算值之间存在一定的误差.

综合以上分析结果对接头的设计方法及施工工艺给出如下建议:① 工程中接头截面的设计是能满足刚度要求的,设计时可以通过调整截面惯性矩来实现设计要求;② 上端刚接约束条件下接头的内力分布较均匀,接头最大变形小,对材料的利用率较高,建议加强对接头上端的约束,设计时可以通过增设Ⅱ型接头翼缘内部多排螺栓，加强其与导墙连接及加强接头露出导墙部位约束来增强约束.

4结论

1) 运用等值梁法对Ⅱ型接头在地下连续墙槽段施工过程中的力学性能进行分析,通过运用极限平衡理论及公式推导,提出了Ⅱ型地下连续墙接头的内力及变形计算公式.该计算公式可以给独立于槽段施工的其他接头提供参考.

2) 结合背景工程,建立了分析Ⅱ型地下连续墙接头施工过程的三维有限元模型,通过有限单元法计算的理论值与公式计算的计算值进行对比,表明计算值具有一定的可靠度,可为该类新型接头施工过程中受力的变形控制提供理论计算依据.

3) 通过对接头上端2种约束形式进行计算,发现上端2种不同的约束形式对接头的力学性能影响较小,但是相比于上端铰接连接形式,采用上端刚接约束时接头内力分布更趋均匀,材料利用率更高.

参考文献(References)

[1]Town P. Controlling water ingress through diaphragm wall joints [C]//ProceedingsoftheFourthInternationalConferenceonGroutingandDeepMixing. New Orleans, USA, 2012:1995-2002.

[2]诸以惇, 陈卫忠, 田洪铭,等. 考虑连续墙接头效应的软土大型盾构工作井稳定性分析[J]. 岩土力学, 2011, 32(10):2937-2943.

Chu Yidun, Chen Weizhong, Tian Hongming, et al. Stability analysis of large shield working well considering effect of diaphragm wall joint [J].RockandSoilMechanics, 2011, 32(10): 2937-2943. (in Chinese)

[3]El-Razek M E A. New method for construction of diaphragm walls [J].JournalofConstructionEngineeringandManagement, 1999, 125(4): 233-241.

[4]Mendez J A, Rausche F, Asce M, et al. Quality control of diaphragm walls by crosshole sonic logging [C]//Full-ScaleTestingandFoundationDesign. Oakland, USA, 2012: 650-663.

[5]Heijmans R W M G, Jansen J A G, Konijnenbelt P, et al. Application of expansion joints in diaphragm walls-VleuGel project[C]//Underground—TheWaytotheFuture. Boca Raton: Taylor & Francis Group, 2013:1633-1640.

[6]丛蔼森.地下连续墙的设计施工与应用[M].北京:中国水利水电出版社,2001:848-869.

[7]王卫东,王建华. 深基坑支护结构与主体结构相结合的设计、分析与实例[M]. 北京:中国建筑工业出版社,2007:46-50.

[8]中建八局第三建设有限公司.一种型钢混凝土柱式接头及采用该接头的地下连续墙的施工方法:中国,CN102561404A[P]. 2012-07-11.

[9]Bryson L S, Zapata-Medina D G. Finite-element analysis of secant pile wall installation [J].ProceedingsoftheInstitutionofCivilEngineers—GeotechnicalEngineering, 2010, 163(4): 209-219.

[10]Chen J J, Lei H, Wang J H. Numerical analysis of the installation effect of diaphragm walls in saturated soft clay [J].ActaGeotechnica, 2014, 9(6): 981-991.

[11]Schafer R, Triantafyllidis T H. The influence of the construction process on the deformation behavior of diaphragm walls in soft clayed ground [J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2006, 30(7): 563-576.

[12]Conti R, de Sanctis L, Viggiani G M B. Numerical modelling of installation effects for diaphragm walls in sand [J].ActaGeotechnica, 2012, 7(3): 219-237.

[13]Lei G H, Sun H S, Ng C W W. An approximate analytical solution for calculating ground surface settlements due to diaphragm walling [J].ComputersandGeotechnics, 2014, 61:108-115.