混频数据回归模型的分析技术及其应用

于　扬，王维国

(1.东北财经大学 经济学院，辽宁 大连116025； 2.内蒙古财经大学 统计与数学学院，内蒙古 呼和浩特010070)



混频数据回归模型的分析技术及其应用

于扬1，2，王维国1

(1.东北财经大学 经济学院，辽宁 大连116025； 2.内蒙古财经大学 统计与数学学院，内蒙古 呼和浩特010070)

摘要：依据混频数据计量经济模型的设置原理，结合传统回归模型推导出了混频数据回归模型的基本形式及拓展形式。概括、梳理出权重多项式函数的几种形式和性质，并结合传统自回归分布滞后模型的估计方法，给出了非限制性混频数据回归模型的最小二乘识别方法及待估参数的检验方法，在此基础上构建了混频数据自回归分布滞后模型MIDAS-ARDL，并利用其对中国月度通货膨胀率进行短期预测。研究表明：MIDAS-ARDL模型在中国通货膨胀的短期预报方面具有较高的精确性和时效性，预测效果优于传统计量经济模型AR(1，13)。

关键词：MIDAS类模型；MIDAS识别方法；通货膨胀

一、引言

金融危机对实体经济的影响被一些采用传统时间序列模型的预测者严重低估，其后果会导致预测偏差的增大，甚至会出现错误结果。传统时间序列回归模型的缺陷及基础数据频率的不一致性往往使研究人员陷入进退两难的境地，而政策制定者急需一种模型在少损失信息情况下能够将高频金融数据与低频宏观经济数据连接起来。为了解决此问题，Ghysels等人提出了混频数据回归模型(MIDAS)。该模型可以直接将不同频率变量纳入同一模型中，并根据实际高频变量的样本数据，将变量的滞后阶数和权重函数放在一起考虑，从而得到模型的最优参数估计值，克服了传统同频率回归模型的参数缺乏灵活性和时变性的缺点[1]。

混频数据回归模型(MIDAS)弥补了传统时间序列回归模型的不足，随着建模理论和分析技术不断发展和创新，它由最初的一个高频变量预测低频变量逐渐发展到多元混频数据回归预测模型(简记M-MIDAS)、因子混频数据回归预测模型(Factor-MIDAS)、非线性MIDAS预测模型、非限制混频数据回归模型(简记为U-MIDAS)、非限制性混频数据误差修正模型(ECM-MIDAS)、马尔科夫转换混频数据模型(简记为MS-MIDAS)、非限制性马尔科夫转换混频数据模型( 简记MS-U-MIDAS)[2-6]。

MIDAS模型发明之初主要用于金融波动性预测，Ghysels、Santa-Clara和 Valkanov 采用MIDAS模型验证了股票高风险往往伴随着高收益的假说[7]。Asgharian、Hou、Javed应用GARCH-MIDAS模型检验微观变量是否能预测收益率方差的短期波动和长期波动，结果表明：在GARCH-MIDAS模型中包含的高频微观信息能提高预测精度，尤其在波动率的长期预测中，其预测精度更高[8]。后来学者逐渐将MIDAS模型应用于宏观经济分析及预测领域， Frale、Monteforte利用因子混频数据回归模型( FaMIDAS )，通过月度宏观经济变量PMI、M2、对外贸易指数等预测意大利季度GDP[9]。Andreou、Ghysels、Kourtellos选用FaMIDAS预测美国季度GDP的增长率，检验了MIDAS模型中加入金融日数据预测低频变量GDP的可行性及实用性，实证结果显示：与同频率模型相比，MIDAS有更好的表现[10]。

目前，国内学者对MIDAS模型的研究及应用还不多见，最早将MIDAS应用于金融领域的是徐剑刚等，他们利用MIDAS 模型和ABDL模型研究中国股市波动性,实证结果显示：MIDAS模型在预测股市波动方面精确度低于ABDL模型[11]；刘金全等将MIDAS模型应用于宏观经济领域，通过蒙特卡罗模拟的方法证明MIDAS模型在中国宏观经济变量处理上的有效性[12]；刘汉和刘金全构建了预测中国季度 GDP混频数据回归模型 (MIDAS)，得出的实证结论为：MIDAS模型在中国宏观经济总量GDP的季度短期预报方面具有较高精确性，在实时预报方面具有可行性和时效性[13]；耿鹏等用MIDAS(m,k,h)-AR(p)对中国季度GDP进行了实时预测和向前h步短期预测[14]。本文探讨MIDAS预测类模型构建的思想及具体形式，深入剖析其内部结构，并结合传统的回归模型给出混频数据回归模型更一般的形式及几种拓展形式，同时根据混频模型构造的内在机理，梳理总结出权重多项式函数的各种形式和性质。结合传统自回归分布滞后模型的估计方法给出多元混频数据回归模型的最小二乘识别方法，并根据传统回归模型及Ghysels、Sinko、Valkanov的研究思路构建检验混频回归模型参数显著性的统计量[15]。本文将利用混频数据自回归分布滞后模型对中国通货膨胀的月度值进行短期预测。

二、混频数据回归模型的基本形式

(一)一元混频数据回归模型

(1)

简记为：

(2)

i=0,1,…,qm

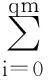
(二)多元混频数据回归模型

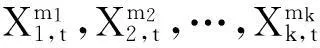
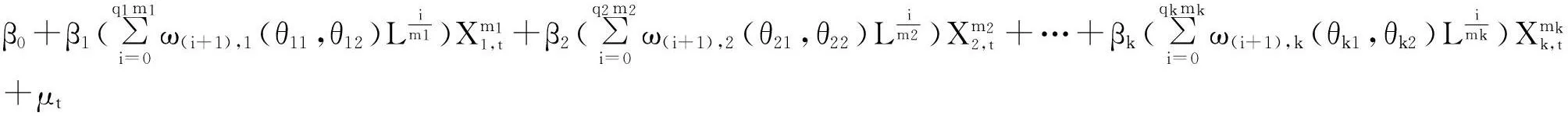
(3)

其中随机扰动项μt是白噪声序列，如果我们令：

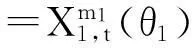
(4)

(5)

⋮

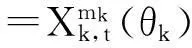
(6)

Yt=Xt(θ)β+μt

(7)

如果用Zt表示与被解释变量同频率的低频变量，则多元混频数据回归模型M-MIDAS的更一般形式为：

Yt=Xt(θ)β+ZtΥ+μt

(8)

Zt=(Z1,t，Z2,t，…，Zp,t)，Υ=(γ1，γ2，…，γp)′

(三)多元混频数据自回归模型

(9)

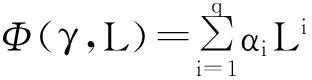
(四)非限制多元混频数据回归模型

当高频变量和低频变量的频率相差很小，且估计的参数不多时，通常选择非限制混频数据回归模型对低频变量做出预测，根据传统分布滞后模型的建模机理，如果高频变量前不加设置权重函数，可得非限制多元混频数据回归模型U-M-MIDAS为：

(10)

其中Yt代表低频变量，X代表高频变量，其中m1,m2,…,mk是第t期到t-1期高频变量样本数据个数，它们之间可以相等也可以不等，q1,q2,…,qk是高频数据的滞后阶数，t代表低频变量具体观测值的时间，且t=1,2,…,T，μt是白噪声序列。

(五)非限制性混频数据误差修正模型

假如非限制性混频数据回归模型中低频因变量与高频自变量存在长期均衡关系，可通过如下变形得到非限制性混频数据误差修正模型。一元非限制性混频数据回归模型的形式为：

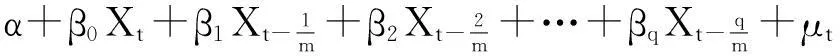
(11)

由上式可知随机误差项为：

则滞后一期随机误差项为：

(12)

(六)马尔科夫转换混频数据回归模型

参照Guerin和Marcellino马尔科夫转换混频数据预测模型(MIDAS)，结合传统的马尔科夫转换模型及混频数据回归模型推导出马尔科夫转换混频数据回归模型[5]:

(13)

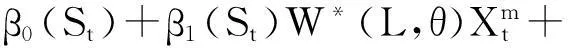
μt(St)

(14)

三、权重多项式函数形式

混频数据回归模型中的权重多项式函数是我们选择适当的数学函数和统计方法将高频数据浓缩成包含大量信息数据集,且剔除了高频数据的微观噪声，这种方法避免了传统方法在建模之前直接将高频数据低频化所带来的损失，实际分析中往往根据权重函数本身具有的特征，将模型中高频解释变量的众多估计参数用该函数表示出来，而这种权重函数含有较少的参数，且权重函数多项式能够收敛到1，使模型中直接引入高频变量成为可能。

(一)Beta-权重函数

选择Ghysels、Santa-Clara、Valkanov 介绍的利用Beta分布族中的概率密度函数表示MIDAS模型的权重函数，因为Beta分布族的概率密度函数只用两个参数就能表现出丰富的类型[1]。

在(C, Βc,p)统计结构中C=(0,1),用Beta函数形式设计具体权重函数形式：

(15)

(二)Almon-权重函数

(16)

阿尔蒙指数滞后多项式的权重形式为：

(17)

权重函数参数和滞后阶数选择非常重要，实际应用中将权重函数的不同形式引入混频数据回归模型中，根据高频数据波动的特点及模型预测精度指标的具体值选择出权重函数最优滞后阶数，同时估计出参数向量的具体值。Ghysels、Santa-Clara和 Valkanov 建议在宏观经济领域进行预测时应采用阿尔蒙指数滞后多项式的权重形式，其预测精度会提高[7]。

(三)利用示性函数表示的MIDAS类模型的权重

用示性函数表示的MIDAS类模型的权重，该权重函数因形式简单而得到广泛应用，其具体形式为：

(18)

其中示性函数Ii∈[bj-1,bp]在i∈[bj-1,bj]时取1，在i∉[bj-1,bj]时取0。使用该权重函数构建的混频回归模型能够度量出高频变量对低频变量的正负冲击。当高频变量对低频变量存在正负冲击差别时，我们选择该权重函数。

(四)双曲线-权重函数

双曲线函数形式的权重函数为:

(19)

由上式可知此权重函数在实际应用中具有局限性，不适用于递增和递减变化的高频样本数据，只实用于先快速递减而后趋于平稳的高频样本数据。

(五)step-function权重函数

分段函数(step-function)表示权重函数的形式为：

(20)

采用高频变量预测低频变量时，如果高频变量存在结构突变点，我们通常选择分段函数表示的权重函数形式将高频样本数据分段，国外研究表明：当金融领域发生巨大波动时，利用此权重函数构建的混频回归模型对低频宏观经济变量预测会更精准。

四、混频数据回归模型的参数识别及检验

(一)非线性混频数据回归模型普通最小二乘估计

混频数据回归模型(MIDAS)最开始是从状态空间模型发展起来的，因此早期研究者通常通过卡尔曼滤波得到参数估计，后来人们对高频变量权重函数添加条件，通常采用Beta分布函数和两参数阿尔蒙指数滞后多项式作为权重函数，利用非线性最小二乘法(简记为NLS)得到参数估计值。非限制性混频数据回归模型的普通最小二乘估计方法主要参照混频数据回归预测模型(MIDAS) 的非线性最小二乘估计方法的内在机理，同时结合Almon提出的范德蒙矩阵，这种方法不像非线性最小二乘法需要事先假定权重多项式之和为1，而是直接利用传统的分布滞后阿尔蒙法识别参数，非限制多变量混频数据回归模型(U-M-MIDAS)的更一般的形式如下：

如果采用Almon提出的范德蒙矩阵，则

(21)

(22)

同理可得如下矩阵形式：

=F2A2

(23)

⋮ ⋮ ⋮

=FkAk

(24)

经过上述变换，原模型可以用如下形式表示：

Yt=β0+F1A1X1+F2A2X2+…+FKAKXK+μt

(25)

如果令XF=Z，则：

(26)

(27)

⋮

(28)

则

Yt=β0+A1Z1+A2Z2+…+AKZK+μt

(29)

即：F1X1=Z1，F2X2=Z2，…，FkXk=Zk。

(二)混频数据模型参数检验

根据约束条件设置Wald统计量：

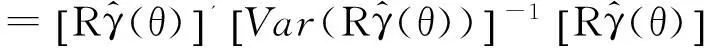
(30)

化简得：

F(J,T-K)

(31)

所以对于混频数据模型参数的显著性，可以通过上述构造的F统计量给予判断。

五、混频数据回归模型的应用

(一)指标选取及数据说明

选取2003年1月到2014年12月低频月度指标黄金价格、工业增加值、房地产综合景气指数、国际石油价格(WTI)、汇率、货币供应量以及2003年1月2日至2014年12月31日上证指数日收盘价作为通货膨胀的重要影响因素。通货膨胀采用居民消费价格指数CPI来度量，利用混频数据回归模型对中国通货膨胀进行样本内及样本外预测。实证结果显示:中国资产价格与通货膨胀之间的关系显著，加入高频资产价格的混频数据回归模型在中国通货膨胀月度预测上具有较高的精度，且其在短期预报及预测方面具有及时性的特点。

(二)基于混频数据回归模型的中国通货膨胀短期预报

本文参照Eric Ghysels的研究成果，选择Beta-权重函数和Almon指数权重函数构建MIDAS 类模型，对两种权重函数参数个数及参数范围进行了约束，参数个数均限定两个，对Beta-权重函数的两个参数θ1、θ2添加了0<θ1<300,0<θ2<300的限制，在选择Almon指数多项式做权重时对参数θ1和θ2施加了θ1≤300,θ2<0的条件，以获得递减型权重函数，保证权重函数的取值为正。利用非线性最小二乘(NLS)最小化MIDAS模型的残差平方和，从而得到最优权重参数及MIDAS模型系数的最优估计值。

权重函数的滞后阶数选择1阶直至40阶，权重函数变动趋势分别选择快速递增、快速递减、先升后降及先降后升来模拟的混频数据回归模型。通过对比预测精度指标均方根误差RMSE，绝对平均误差MAE，绝对误差百分比之平均MAPE泰尔U统计量的值，发现快速递减型阿尔蒙指数多项式权重函数变化到31阶时，混频数据回归模型的拟合结果表现最优。选择的估计方法为非线性最小二乘法(NLS)。 模型的优劣采用前面推导出来的混频数据回归模型参数显著性检验的方法，实证过程中根据t统计量和F统计量是否显著选择解释变量，并根据预测精度确定低频变量和高频变量的滞后阶数。通过对比最后得到最优模型如下：

(32)

实证研究表明：递减型Almon指数多项权重函数构建的混频数据回归模型在拟合结果和预测精度上表现最优，且当递减型权重函数的滞后阶数变动到31阶时，我们设置的混频模型的统计量拟合优度最大，模型的拟合结果最好。

表1　权重函数滞后31阶混频数据回归模型的拟合结果

注：中括号内数值为t值。

混频数据回归模型结果表明:中国通货膨胀的变动具有一定惯性，本期通货膨胀受上一期的影响显著，影响程效应达0.842 9。资产价格和股票价格对通货膨胀有显著正影响，根据传统理论，股票价格上升，投资者就会增加投资，投资增加会带动经济增长，致使通货膨胀率会上升。同时，股票价格上升，会增加投资者的资产，资产的增加会对消费产生促进作用，居民的消费水平会上升，从而促使通货膨胀率增加。实证结果与传统理论相符。这说明股票价格存在财富效应，即股票价格上涨会通过财富效应路径促进家庭消费增加，从而带动总需求变大，推高了物价水平。

根据表1给出参数估计值可知通货膨胀受股票价格影响的动态总乘数效应为0.000 2，房地产价格上涨分担了代表家庭消费商品和劳务的价格变动CPI，当期房地产价格对通货膨胀没有发挥出作用，滞后一期与通货膨胀之间呈现负向关系；工业增加值对通货膨胀没有即期乘数效应，其延迟一期工业增加值的乘数效应为0.091 3；滞后期5期的货币供应量的变化会加速通货膨胀，货币供应量每增加1个百分点，物价将随之上升 0.063 1个百分点，中国受国际石油价格及汇率变化对通货膨胀的影响存在不稳定性。滞后两期和滞后五期的国际石油价格与通货膨胀负相关，而滞后三期的国际石油价格与通货膨胀正相关；黄金价格对通货膨胀影响微弱。

由表2可知，递减型Almon指数权重函数的滞后阶数从1阶变到40阶时，混频数据回归模型的调整拟合优度和AIC、SC的变化情况由表2中数据可知：当权重函数的滞后阶数变动到31阶时，调整拟合优度达到最大，AIC、SC的值达到最小。

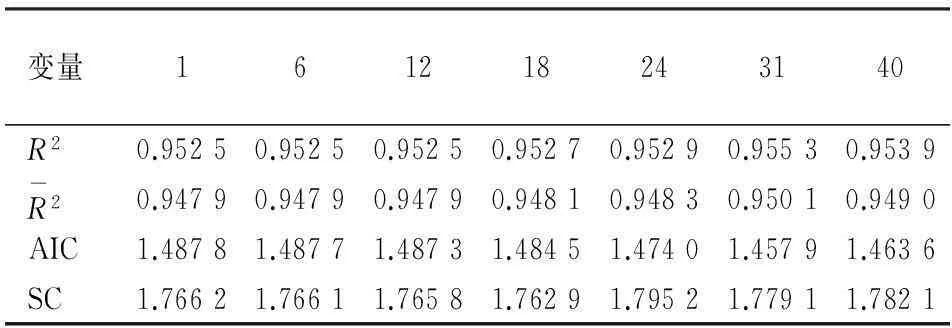
表2　不同滞后阶数混频回归模型的拟合指标值

本文选择均方根误差(简记为RMSE)、绝对平均误差(简记为MAE)、平均绝对百分比误差(简记为MAPE)和泰尔U统计量来评价模型预测精度。当统计指标估计值越小时，表明模型的可靠性越高，预测精度越高，预测结果越好，其中：

我们将混频数据回归模型的预测精度和梳系数自回归模型AR(1，13)的预测精度做比较，如表3所示。梳系数自回归模型AR(1，13)对通货膨胀的调整拟合优度达0.914 4，但其预测精度四个指标值均高于混频数据回归模型，这说明混频数据回归模型在对中国通货膨胀的预测上具有优势。

表3　混频数据回归模型和梳系数自回归

六、混频数据回归模型的优势及未来发展方向

混频数据回归模型(MIDAS)的分析框架比传统回归模型有更强的灵活性，它能够直接将高频数据和低频数据引入模型中，它能捕捉到高频数据的内在信息，并能将这种信息得以最大化的利用，避免了为了化成同一频率而使全样本信息损失和设定的一些误差。它能够改变传统时间序列回归模型低频数据预测的时滞性，使利用最新高频数据的解释变量快速预测出低频被解释变量成为可能，避免了因经济变量数据公布的时滞性而无法及时准确地对当前宏观经济状态和宏观经济走势进行判断，改进了宏观经济预报的时效性和短期预测的精确性。它可以根据具体高频数据的特征，利用计算机模拟得到合理的滞后阶数，从而得到比较精确的估计参数。

本文对相关文献及研究进行了系统梳理概括，并结合传统的回归模型给出了混频数据回归模型更一般的形式。本文根据混频模型构造的内在机理给出了权重多项式函数的各种形式和性质，并结合传统自回归分布滞后模型的估计方法，给出了多元混频数据回归模型的最小二乘识别方法和参数的检验方法。本文利用高频资产价格等指标构建混频数据回归模型，对中国通货膨胀进行了短期预测，并将预测结果与传统模型进行对比，结果表明：我们构建的混频数据回归模型在中国通货膨胀的月度预报方面具有较高的时效性和精确性，其预测精度优于传统基准模型梳系数自回归AR(1,13)。

国际计量经济学界十分重视混频数据建模理论与分析技术，经过近几年的发展，混频数据回归模型已经成为研究不同频率经济之间联系的热点问题，在许多方面积累了大量的研究成果，建模理论和分析技术不断发展和更新。混频数据计量模型在宏观经济预测、微观经济波动的度量以及宏观经济与微观经济的内在联系等领域的应用得到了快速的发展，混频数据回归模型所囊括样本数据的丰富动态特征是传统同频率模型无法比拟的。在宏观经济和金融市场紧密结合的今天，混频数据回归模型无论在实时预测、结构分析还是一些政策评价上都显得非常重要，因此，今后混频数据回归模型的分析理论及建模技术将与面板数据模型结合起来分析和预测宏观经济的走势，这也是本文将继续研究的方向。

参考文献：

[1]Ghysels E，Santa-Clara P，Valkanov R.The MIDAS Touch: Mixed Data Sampling Regression Models[R].Working Paper，UC Los Angeles，2002.

[2]Ghysels E，Valkanov R.MIDAS Regressions: Further Results and New Directions[J].Econometric Reviews，2006(2).

[3]Marcellino M，Schumacher C.Factor MIDAS for Nowcasting and Forecasting with Ragged-Edge Data: A Model Comparison for German GDP[J].Oxford Bulletin of Economics and Statistics，2010，72(4).

[4]Thomas B，Hecq A，Urbain J.Forecasting Mixed Frequency Time Series with ECM-MIDAS Models[J].Department of Quantitative Economics，2011(2).

[5]Guérin P，Marcellino M .Markov Switching MIDAS Models[J]. Journal of Business and Economic Statistics，2013(1).

[6]Barsoum F，Stankiewicz S. Forecasting GDP Growth Using Mixed-Frequency Models With Switching Regimes[J]. International Journal of Forecasting,2015(7).

[7]Ghysels E，Santa-Clara P，Valkanov R. There is a Risk-return Trade-off after All[J]. Journal of Financial Economics，2005，76(3).

[8]Asgharian H，Hou A，Javed F.Importance of the Macroeconomic Variables for Variance Prediction GARCH-MIDAS Approach[R]. Kunt Wicksell Working Papers，2013.

[9]Frale C，Monteforte L .FaMIDAS: A Mixed Frequency Factor Model with MIDAS Structure[R].Working Paper，2011.

[10]Andreou E，Ghysels E，Kourtellos A.Should Macroeconomic Fore-casters Use Daily Financial Data and How? [J].University of Cyprus WP，2010(9).

[11]徐剑刚，张晓蓉，唐国兴.混合数据抽样波动模型[J].数量经济技术经济研究，2007(11).

[12]刘金全，刘汉，印重.中国宏观经济混频数据模型应用[J].经济科学，2010(5).

[13]刘汉，刘金全.中国宏观经济总量的实时预报与短期预测[J].经济研究，2011(3).

[14]耿鹏,齐红倩.中国季度 GDP 实时数据预测与评价[J].统计研究,2012(1).

[15]王佐仁，石倩.关于多维指标抽样调查中删除指标的均值估计[J].统计与信息论坛，2014(8).

Analysis and Application of MIDAS Model

YU Yang1,2， WANG Wei-guo1

(1. School of Ecomomics，Dongbei University of Finance and Ecomomics，Dalian 116025, China;

2. School of Statistics and Mathematics，Inner Mongolin University of Finance and Ecomomics， Huhhot 010070，China)

(责任编辑：李勤)

王维国，男，辽宁大连人，经济学博士，教授，研究方向：计量经济分析。

【统计理论与方法】

Abstract:According to the principle of mixed frequency regression model and the traditional common low frequency model，this paper has been deduced the basic form and expanded form of MIDAS model. Several types of the weighting polynomial function and natures have been tease out. Combined the traditional estimation of autoregressive distributed lag model with MIDAS model，the ordinary least squares estimation of U-MIDAS and parameters of testing method have been given.Based on this, inflation's monthly short-term value in China has been predicted with MIDAS-ARDL model.The results show that MIDAS-ARDL has high accuracy and timeliness of the characteristics，which prediction effect is superior to the traditional econometric AR(1,13)model.

Key words:MIDAS models；MIDAS estimation method；inflation

中图分类号：F224.0∶O212.1

文献标志码：A

文章编号：1007-3116(2015)12-0022-09

作者简介：于扬，女，内蒙古呼和浩特人，博士生，讲师，研究方向：计量经济分析；

基金项目：国家自然科学 《基于结构突变和截面相关的省际碳排放面板协整检验方法》(71171035)；国家社会科学 《SNA(2008)框架下FISIM核算方法的改进、拓展与中国实践研究》(2014SDXT013)；内蒙古自然科学基金项目《蒙特卡洛方法在贝叶斯随机波动预测模型中的应用》(2014MS0701)

收稿日期：2015-09-18