基于随机效应零调整回归模型的保险损失预测
2016-01-27孟生旺李政宵
孟生旺,李政宵
(中国人民大学 a.应用统计科学研究中心;b.统计学院, 北京100872)
基于随机效应零调整回归模型的保险损失预测
孟生旺a,b,李政宵a,b
(中国人民大学 a.应用统计科学研究中心;b.统计学院, 北京100872)
摘要:在非寿险精算中,对保单的累积损失进行预测是费率厘定的基础。在对累积损失进行预测时通常使用Tweedie回归模型。当损失观察数据中包含大量零索赔的保单时,Tweedie回归模型对零点的拟合容易出现偏差;若用零调整分布代替Tweedie分布,并在模型中引入连续型解释变量的平方函数,可以建立零调整回归模型;如果在零调整回归模型中将水平数较多的分类解释变量作为随机效应处理,可以进一步改善预测结果的合理性。基于一组机动车辆第三者责任保险的损失数据,将不同分布假设下的固定效应模型与随机效应模型进行对比,实证检验了随机效应零调整回归模型在保险损失预测中的优越性。
关键词:零调整分布;Tweedie分布;随机效应;累积损失
一、引 言
非寿险精算的核心工作之一是进行保险损失预测,它是非寿险定价和准备金评估的基础。目前使用最广泛的保险损失预测工具是广义线性模型[1]15-21。
广义线性模型假设因变量服从指数分布族,该分布族包含了很多保险损失预测中最常使用的一些分布,如泊松分布、负二项分布、伽马分布、逆高斯分布和Tweedie分布等。在预测事故发生概率时,通常使用二项分布假设;在预测索赔次数时,通常使用泊松分布或负二项分布假设;在预测损失金额时,通常使用伽马分布或逆高斯分布假设;在预测累积损失时,通常使用Tweedie分布假设[2]127-128。
在保险产品定价过程中,通常需要预测保单的累积损失,即一份保单在一个保险期间的损失之和。通常的做法是首先应用泊松回归或负二项回归模型预测损失频率,然后应用伽马回归或逆高斯回归模型预测平均每次损失的损失金额,再将两者相乘得到累积损失的预测值,这种做法隐含着一个重要假设,即损失频率和损失金额之间是相互独立的,在实际应用中这种独立性假设很难得到保证。某些损失频率偏低保单,平均每次的损失金额可能较大,而一些损失频率偏高的保单,平均每次的损失金额可能较小[3]。
预测累积损失的另外一种方法是建立Tweedie回归模型[4-6]。Tweedie分布是损失次数服从泊松分布、每次的损失金额服从伽马分布假设下的累积损失分布。Tweedie回归模型直接对累积损失进行建模,所以无需假设损失次数与损失金额相互独立。但是,Tweedie回归模型也有其局限性,即在预测累积损失在零点的概率时可能出现较大偏差。在许多保险业务中,大量保单在保险期间不会发生任何损失,这就使得保单的累积损失观察值在零点有一个很高的概率堆积,远远大于Tweedie分布在零点可能达到的概率值。此外,在Tweedie回归模型中,零点的概率不易引入其他协变量进行解释,模型的灵活性也会受到一定影响。
预测累积损失的另一种方法是建立零调整回归模型,即在累积损失服从零调整分布的假设下建立回归模型[7]。常用的零调整分布包括零调整伽马分布、零调整逆高斯分布和零调整对数正态分布。零调整分布可以看做是伯努利分布与一个连续分布的混合分布,其中伯努利分布用于描述损失是否发生,而连续型分布用于描述在损失发生情况下累积损失金额的分布。
在给定均值和方差的条件下,逆高斯分布的偏度系数大于伽马分布,对数正态分布的偏度系数大于逆高斯分布。伽马分布和逆高斯分布都是尺度分布,所以基于这两个分布假设建立的回归模型不会因为损失金额的计量单位不同而扭曲模型的参数估计值,而对数正态分布不是尺度分布,损失金额使用不同的计量单位会得到不同的回归参数估计值。在损失发生的情况下,如果累积损失具有明显的尖峰厚尾特征,则零调整逆高斯回归模型要优于零调整伽马回归;如果累积损失的厚尾特征不明显,则零调整伽马回归模型可能更优。与Tweedie回归模型相比,零调整回归模型的优点是可以对零点的概率和累积损失的均值同时建立回归模型[8]。
在损失预测模型中,当某个分类解释变量在各个水平上的观察数据足够充分时,该变量既可以作为固定效应处理,也可以作为随机效应处理。但是,当一个分类变量包含数十个甚至上百个水平时,某些水平上的观察数据可能很少甚至没有观察数据,在这种情况下将其作为随机效应处理可能更加合理,因为随机效应具有类似信度模型的“收缩估计”性质,估计结果更加稳健[9-10]。
有鉴于此,本文主要对零调整回归模型进行推广,并讨论该模型在累积损失预测中的应用。本文对零调整回归模型的推广包括两方面的内容:一方面是把水平数较多的分类解释变量作为随机效应处理,增加预测结果的稳健性;另一方面是把连续型解释变量进行平滑处理,提高预测的准确性。本文基于一组实际车损险数据进行实证研究,结果表明,随机效应零调整回归模型对累积损失的预测要优于通常使用的Tweedie回归模型,在一定程度上也优于固定效应的零调整回归模型。
二、随机效应Tweedie回归模型
在累积损失的预测中,通常分别建立损失频率和损失金额的回归模型,然后将它们的预测结果相乘得到累积损失的预测结果。这种方法的优点是可以分别对损失频率和损失金额进行预测,揭示损失频率和损失金额的不同影响因素,有利于风险的识别和管理,不足之处是忽略了损失频率与损失金额之间可能存在的相依关系。如果损失频率与损失金额之间的相依关系较强,可以考虑采取两种方法处理:一种是通过copula函数建立损失频率与损失金额之间的相依关系[11-12];另一种是应用Tweedie回归直接建立累积损失的预测模型。
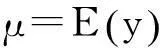


其中
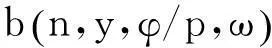

Tweedie分布的期望与方差分别表示为:
其中,φ为离散参数。Tweedie分布通过参数p来调节分布的方差,并影响分布的过离散结构。譬如,当p=0时,Tweedie分布就退化为正态分布;当p=1和2时,Tweedie分布分别对应泊松分布和伽马分布;当p=3时,Tweedie分布就退化为逆高斯分布;当1 通过上式中的密度函数,可以求得相应的对数似然函数。注意,在没有损失发生的情况下,即当n=0、y=0时,相应的对数似然函数为: 若把均值参数表示为解释变量的函数,并使用对数连接函数,即可建立下述的固定效应Tweedie回归模型: 其中,μi表示对第i份保单的累积损失的预测值,xi为第i份保单的解释变量,β为回归系数。 在固定效应模型的基础上,进一步假设某些回归参数是随机的,就可以得到所谓的随机效应回归模型。在随机效应模型中,相当于用一个分类变量把所有保单进行了分类,并且假设不同类别的回归系数是不同的。如果仍然使用对数连接函数,则随机效应Tweedie回归模型可以表示为: 三、随机效应零调整回归模型 在对累积损失数据建立回归模型时,通常使用Tweedie分布假设,但在某些情况下,零调整回归模型对累积损失数据的拟合效果可能更优[13]197-198。零调整回归模型根据连续型分布的不同,可以分为零调整伽马回归模型与零调整逆高斯回归模型。 零调整伽马分布是在零点的退化分布与伽马分布形成的混合分布,密度函数可以表示为: 其中,y表示累积损失,μ表示位置参数,σ表示尺度参数,ν表示零膨胀概率,即保单在保险期间没有发生索赔的概率。 零调整伽马分布的均值和方差分别为: 如果累积损失具有明显的尖峰厚尾特征,则零调整逆高斯分布的拟合可能优于零调整伽马分布。零调整逆高斯分布是在零点的退化分布与逆高斯分布形成的混合分布,密度函数可以表示为: 其中,y表示累积损失,μ表示位置参数,σ表示尺度参数,ν表示零膨胀概率。 零调整逆高斯分布的均值和方差分别为: 在上述零调整分布的均值和零调整概率中分别引入协变量,即可建立均值μi和零调整概率vi的回归模型如下: 其中,xi表示均值回归模型中的解释变量;ri表示零调整概率回归模型中的解释变量;β和α分别表示均值模型和零调整概率模型中的回归系数。μi和vi分别表示对第i份保单的均值预测值和零调整概率预测值。 与随机效应Tweedie回归模型类似,随机效应零调整回归模型是指在前述的均值回归部分引入随机效应,即表示为: 在下文的数据分析部分,本文使用的随机效应模型可以简化为随机截距回归模型。上式的随机效应uj是指保单持有人的居住地区,即模型的截距项随着居住地区的不同而变化。 四、模拟分析与实际应用 (一)模拟数据分析 σ=0.5ν=0.6 其中,β0=6,β1=0.002 5,以后的参数值依次增加0.002 5,即β2=0.005,…,β400=1。 对该模拟数据分别建立固定效应和随机效应的零调整伽马回归模型。在固定效应模型中,将车型变量作为普通的分类变量处理;在随机效应模型中,将车型变量作为随机效应处理,并且假设随机效应服从均值为0的正态分布。 固定效应和随机效应模型的AIC分别为356 550和356 521,预测均方误差分别为380 005和377 882,这就表明,将水平数很多的分类解释变量作为随机效应处理,可以改善模型的拟合效果。 (二)实际损失数据的描述 下面对一组机动车辆第三者责任险的累积损失数据进行分析[10]。原始数据包括9个解释变量,分别是行驶区域、发动机功率、汽车品牌、油耗类型、居住地区、奖惩系数、人口密度、车龄、驾驶人年龄,其中行驶区域、发动机功率、汽车品牌、油耗类型、奖惩系数、居住地区是分类变量,分别包含6、12、11、2、2、22个水平,见表 1。 表1 解释变量及其水平 原始数据集中共有670 397条损失记录,其中包含同一保单发生的多次损失记录。如果将同一保单发生的多次损失合并就可以得到每份保单的累积损失观察值,合并后的数据集共有668 897份保单的累积损失观察值。为了保证预测模型的稳健性,将累积损失大于100万的3份保单的数据作为异常值删除,最终得到668 894份保单的累积损失数据,其中643 953份保单的累积损失为零,占保单总数的96.27%,表明累积损失数据在零点有一个很大的概率堆积。图1的直方图描述了在损失发生的条件下,每份保单在保险期间的累积损失的观察值。为了图示效果更加清晰,该图仅呈现了累积损失小于15 000元的数据,可以看出,经验累积损失呈现出明显的右偏特性,图1表明累积损失的对数存在比较明显的对称特性。对于每份保单的累积损失数据,分别用零调整伽马分布、零调整逆高斯分布和Tweedie分布进行拟合,求得它们的AIC统计量分别为644 004、647 843和655 177,表明零调整伽马分布对这组累积损失数据的拟合效果相对较好。 图 1 累积损失的经验分布 (三)模型选择 本文研究的数据集共有668 894份保单,每份保单的观察值既包含累积损失,也包含9个解释变量,其中车龄、驾驶人年龄是连续型变量,其他是分类变量。下面以累积损失为因变量,以发动机功率、油耗类型、车龄、驾驶人年龄、汽车品牌以及居住地区为解释变量,分别建立零调整回归模型和Tweedie回归模型。经检验,所有解释变量的交互项在统计上都不显著,所以在下述建立的回归模型中不考虑交互效应。为了方便表述,下面用ZAIG表示零调整逆高斯分布,用ZAGA表示零调整伽马分布,用Tweedie表示Tweedie分布。居住地区变量共有22个水平,水平数较多,下面分别将其作为固定效应和随机效应建立ZAIG回归模型、ZAGA回归模型与Tweedie回归模型。 在不同模型的比较和选择中,通常使用AIC准则和BIC准则,其中AIC=-2l+2p,BIC=-2l+plnn,l是对数似然函数的值,p为模型的参数个数,n为样本量。AIC和BIC的数值越小,表明模型对实际数据的拟合效果越好。AIC和BIC均引入了与模型参数个数相关的惩罚项,但BIC考虑了样本量,当样本量很大时,BIC准则对参数个数的惩罚比AIC准则更为严格。 表2给出了六种回归模型的拟合优度统计量。固定效应模型将居住地区变量作为固定效应处理,随机效应将居住地区作为随机截距项处理,允许不同居住地区的截距项不同。零调整回归模型的优势在于可以对零值的概率建立回归模型,解释变量包括车龄、驾驶人年龄、汽车品牌、发动机功率和居住地区。表2的结果表明,零调整回归模型的AIC和BIC都远远小于Tweedie回归模型,表明零调整回归模型的拟合效果优于Tweedie回归模型。在零调整回归模型中,ZAGA模型的AIC小于ZAIG模型,表明本例的损失数据的尖峰厚尾特征并不明显,ZAGA模型的拟合相对较好。进一步比较AIC统计量,固定效应ZAGA与随机效应ZAGA差异并不明显;但比较BIC统计量,随机效应ZAGA小于固定效应ZAGA,表明对于本例的实际数据而言,随机效应ZAGA回归模型略优于固定效应ZAGA回归模型。 表2 回归模型的拟合效果比较 基于上述的分析与比较,本文最终选定的模型是随机效应零调整伽马回归模型,模型的设定与最终形式如式(1)和式(2)所示,分别表示对零调整伽马分布的均值和零调整概率建立的回归模型,其中均值回归模型中使用对数连接函数,零调整概率回归模型中使用logit连接函数。 (1) (2) 在式(1)和式(2)中,下标i表示不同的发动机功率,k表示不同的汽车品牌,j表示不同的居住地区,l表示不同的油耗类型;uj为随机效应,服从均值为0的正态分布;允许模型的截距项随着居住地区的不同而变化。由于驾驶人年龄和车龄是连续型解释变量,它们对累积损失和损失发生概率的影响并非简单的线性关系,所以引入了二次方函数描述它们的非线性效应。 表3是随机效应ZAGA模型中均值回归参数和零调整概率回归参数的估计结果,其中均值回归模型的居住地区变量下各个水平的值为随机效应的预测值。可以看出,驾驶人年龄、发动机功率、汽车品牌以及居住地区对累积损失的大小有显著影响,同时驾驶人年龄、车龄、汽车品牌、油耗类型以及居住地区对损失发生的概率具有显著影响,其中居住地区在均值回归部分作为随机效应处理,在零调整概率的回归部分作为固定效应处理。在损失发生概率的回归模型中,居住地区11作为基准项,因此其参数估计值为零。图2显示了驾驶人年龄和车龄对累积损失与损失发生概率的非线性影响,其中灰色部分是估计的上下界。从驾驶人年龄来看,在48岁之前,随着驾驶人年龄的增加,累积损失逐渐降低,损失发生的概率也随之降低;驾驶人年龄超过48岁后,驾驶人年龄与累积损失之间成正相关关系,驾驶人年龄越大发生损失的概率越高,累积损失也随之增加。车龄与损失发生概率之间具有较为明显的负相关关系,即车辆使用年限越长,损失发生的概率越低。但是,对于车龄在8年以内的车辆,车龄越长发生损失的概率越高。 表3 随机效应ZAGA回归模型的参数估计值 注:*表示在显著性水平为0.05的情况下估计结果显著;均值回归参数中的居住地区作为随机效应,其值属于预测值,故不考虑显著性。 图2 驾驶人年龄和车龄对累积损失和损失发生概率的非线性影响 图3对固定效应ZAGA和随机效应ZAGA回归模型的预测值进行了比较,数据共包含3 884个风险类别,结果表明,随机效应模型与固定效应模型在总体上对各个风险类别的预测差别不大,但随机效应模型的预测值更加靠近总体平均水平,预测值的波动范围相对较小,这正好体现了随机效应模型的收缩估计性质,即当某个风险类别的观察数据较少时,模型对该风险类别的预测值将被拉向总体平均水平[9]。本例的数据量较大,每个风险类别都具有较为充足的观察数据,所以固定效应与随机效应的预测值差异不是很大。 图3 固定效应与随机效应ZAGA回归模型的预测值比较 五、结论 在非寿险定价中,纯保费的厘定至关重要,而纯保费的合理厘定与累积损失的预测密切相关。累积损失的预测通常使用Tweedie回归模型,但是当数据中包含大量零索赔的保单时,Tweedie回归模型由于无法对零点的概率建立回归模型,从而使得对零值的拟合容易出现偏差。零调整回归模型不仅可以对累积损失的均值建立回归模型,而且可以对零点的概率建立回归模型,因此对累积损失的拟合要优于Tweedie回归模型。 与固定效应模型相比,随机效应模型的预测值具有“收缩估计”的稳健性质。若将水平数很多的分类解释变量作为随机效应处理,模型的拟合效果会进一步得到改善。 连续型解释变量对因变量的影响可能是非线性的形式,在这种情况下如果采用简单的线性关系建立回归模型,往往会降低模型的预测精度。对于具有非线性影响的连续型解释变量,在回归模型中可以采用多项式或样条函数的形式。 本文以机动车辆第三者责任保险的损失数据为例,讨论了随机效应零调整回归模型在损失预测中的应用,分析结果表明该模型对累积损失的拟合效果优于Tweedie回归模型,在一定程度上也优于固定效应回归模型。 参考文献: [1]Ohlsson E, Johansson B. Non-life Insurance Pricing with Generalized Linear Models[M]. Heidelberg: Springer,2010. [2]De Jong P, Heller G Z. Generalized Linear Models for Insurance Data[M]. London: Cambridge University Press, 2008. [3]Bignozzi V, Puccetti G, Rüschendorf L. Reducing Model Risk Via Positive and Negative Dependence Assumptions[J]. Insurance: Mathematics and Economics, 2015,61(1). [4]Gschlößl S, Czado C. Spatial Modelling of Claim Frequency and Claim Size in Insurance[J].Scandinavian Actuarial Journal, 2007 (3). [5]Jørgensen B, Paes De Souza M C. Fitting Tweedie's Compound Poisson Model to Insurance Claims Data[J]. Scandinavian Actuarial Journal, 1994(1). [6]Smyth G K. Fitting Tweedie's Compound Poisson Model to Insurance Claims Data: Dispersion Modelling[J]. Astin Bulletin, 2002, 32(1). [7]Heller G Z, Stasinopoulos D M, Rigby R A. The Zero Adjusted Inverse Gaussian Distribution as a Model for Insurance Data[C]. Proceedings of the International Workshop on Statistical Modelling, 2006. [8]孟生旺, 王选鹤. Gamlss模型及其在车损险费率厘定中的应用[J]. 数理统计与管理, 2014, 33(4). [9]Frees E W, Young V R, Luo Y. A Longitudinal Data Analysis Interpretation of Credibility Models[J]. Insurance: Mathematics and Economics, 1999, 24(3). [10]Antonio K, Beirlant J. Actuarial Statistics with Generalized Linear Mixed Models[J]. Insurance: Mathematics and Economics, 2007, 40(1). [11]Frees E W, Valdez E A. Understanding Relationships Using Copulas[J]. North American actuarial journal, 1998, 2(1). [12]孟生旺, 刘新红. 基于 copula 回归模型的损失预测[J]. 统计与信息论坛,2013, 28(9). [13]孟生旺. 汽车保险的精算统计模型[M]. 北京: 中国统计出版社,2014. (责任编辑:崔国平) 李政宵,男,四川成都人,博士生,研究方向:非寿险精算与统计模型。 【统计理论与方法】 Prediction of Insurance Loss Based on Zero-Adjusted Random-Effect Regression Models MENG Sheng-wanga,b, LI Zheng-xiaoa,b (a.Center for Applied Statistics; b. School of Statistics, Renmin University of China, Beijing 100872, China) Abstract:In classification ratemaking of general insurance, the insurance company mainly focuses on predicting the aggregate claim losses of polices. The main method of predicting aggregate loss is establishing Tweedie regression model.However, Tweedie regression model may produce large deviations when predicting zero-claim numbers, as the zero-claim has a very high probability, far greater than the probability at zero in Tweedie distribution. Based on the assumption that aggregate insurance loss follows zero-adjusted distribution, zero-adjusted regression model can be established. If a categorical variable that contains too many levels is treated as random effect, and also introduces quadratic function of continuous variables in the regression, the accuracy of prediction can be further improved. Based on the empirical study of motor third-party liability insurance loss, several regression models with random or fixed effects are compared under different distributions, the empirical results shows that zero-adjusted random-effect regression models have superiority in predicting insurance loss. Key words:zero-adjusted distribution; Tweedie distribution; random effect; aggregate loss 中图分类号:F840∶O212 文献标志码:A 文章编号:1007-3116(2015)12-0003-07 作者简介:孟生旺,男,甘肃秦安人,经济学博士,教授, 博士生导师,研究方向:应用统计,风险管理与精算; 基金项目:国家自然科学 《考虑风险相依的非寿险精算模型研究》(71171193);教育部重点研究基地重大项目《随机效应模型及其在非寿险风险管理中的应用》(12JJD790025) 收稿日期:2015-07-31