基于通联累积量的动态网络异常检测算法

贺　亮，褚衍杰，韩杰思

(盲信号处理重点实验室，四川 成都 610041)



基于通联累积量的动态网络异常检测算法

贺亮，褚衍杰，韩杰思

(盲信号处理重点实验室，四川 成都 610041)

摘要：在网络运维管理领域，最受关注的问题之一是如何及时发现网络异常。针对现有方法难以发现异常的高频次通联行为的问题，提出一种基于统计模型的高频通联异常检测方法，以幂律分布模型来描述网络中节点数与频繁通信次数之间的关系，通过线性回归方法进行拟合，并将回归误差超出置信度范围的网络状态判定为异常。此外，针对网络中存在重点关注节点对的情况，给出其权重预分配方案；针对规模较小的网络状态，考虑其不完全服从幂律分布，给出样本预筛选策略，用于降低对异常网络状态的虚警率。最终实验结果表明，该方法在低频次通联异常与高频次通联异常条件下，均表现出较高的检测率。

关键词：动态复杂网络；异常检测；通联累计量；线性回归

0引言

随着互联网规模的急剧膨胀，网络攻击、计算机病毒等恶意行为造成的危害愈加严重，有必要针对这些网络异常行为，研究快速、准确的检测方法，以方便网络管理者迅速发现网络异常。在动态复杂网络中，网络节点数以及节点之间的通联关系随时间变化。一方面，异常检测需要从众多网络节点中发现异常节点，从而维护网络安全；另一方面，需要从网络总体上判断当前网络是否异常，从而进一步采取相应措施，例如某局域网通联数突然增加可能表示该网络遭受到了网络恶意攻击入侵，网络管理员需要进一步排查网络中受到入侵的节点。

网络异常是与网络正常状态相对的概念，异常检测的一个基本思想，是通过网络长期稳定的数据对网络的正常行为进行建模，找出短期内与该模型偏离较为严重的网络行为作为网络异常[1]。

网络中的异常种类较多，文献[2]将其分为三类，包括：点异常，即局部异常；上下文异常，即异常与事件发生的时刻有关；联合异常，即一段时间内的异常。文献[3]通过时间序列分析的方法提取数据的微观特征和异常。可以通过网络的特征参数对异常现象进行检测，即测量网络的结构特征监测网络结构是否发生了显著变化，从而发现异常。

网络在运行时，一段时间内的通联次数具有一定的规律，当通联次数有显著增加或减少时，说明网络发生异常。例如，网络中主机遭受病毒攻击后，会频繁发送数据包，引起网络异常。可以通过网络正常运行时的数据总结网络中通联规律，设计异常检测机制判断网络通联异常。异常检测机制可以应用到许多领域，例如，网络管理员可以通过异常检测机制及时发现网络异常，从而对网络中的异常现象进行处理，监察部门可以通过网络通联异常，捕获重要节点的行为。从数据获取的角度看，收集网络中的数据后可以进一步剔除异常数据，获得较为合理的网络数据，方便对网络行为进行建模分析。

异常检测方法主要分为两类：基于统计模型的方法和基于距离的非参数化方法。统计模型方法主要是对网络中的一些参数如结点的度、网络中流量状况等进行建模，得到模型参数后，找出不符合模型的数据点作为异常点[4]，非参数方法则是对网路进行聚类分析后判别网络异常情况[5]。

统计模型方法中，文献[6]采用了自回归滑动平均模型(ARMA模型)，通过观测网络参数，划分时间段构成时间序列，利用时间序列挖掘出的规律来找出异常数据。文献[7-8]对时间序列进行相似性度量，从而根据两个时间序列的距离来判断是否为同一个时间序列数据，文献[9-10]在此基础上进行聚类分析，找出异常时间序列。文献[11]提出的随机图模型中，给出网络中结点度数服从泊松分布这一结论，文献[12]提出的优选选择模型，指出复杂网络的节点度数分布是幂律分布，文献[13]在大量数据集上面统计出图的两个基本规律：幂律特征以及有效直径随时间减小。文献[14]在给出图的相似度定义基础上定义图之间的距离，通过距离来判断图结构是否异常。文献[15]通过挖掘网络的模式，使用序列模式挖掘算法，挖掘网络中频繁出现并且具有先后关系的网络拓扑结构，从而能够挖掘出网络演化规律[16]，找出相应的异常。

文献[17]提出LRAD算法(Linear Regression Anomaly Detection)和iLRAD算法(Iterative Linear Regression Anomaly Detection)，将网络通联频次发生显著变化作为网络异常，对网络正常状态下节点和边数进行回归建模，距离模型较远的数据点作为异常数据点，iLRAD是LRAD的迭代版本，在每次迭代中，都删除当前的异常点重新进行建模。但是，该方法只对网络中两个节点是否通信进行统计，并没有考虑节点之间频繁通信的情况，因此不能检测该类异常。

本文在iLRAD算法的基础上，设计检测频繁通联异常的方法，将网络中通联频次发生显著变化作为网络异常，提出通联累积量检测的LRAD算法 (cumulant Linear Regression Anomaly Detection，cLRAD)，考虑网络中节点之间通信频次作为通联累积量进行异常检测，还可以针对个别重要节点的通信设计权值，当该节点之间发生频繁通信时，相应的异常可能性变大。例如，传统MSTP(Multi-Service Transfer Platform)网络不支持流量的统计与复用并存在多点到多点业务[18]无法进行通过流量进行异常检测，本文方法可对此类网络进行检测。本文接下来的内容安排如下：首先，以幂律分布模型对网络节点数与通联累积量之间的关系进行建模，并在理论上证明其合理性；在此基础上，给出cLRAD算法流程；最后，通过Enron公司邮件数据库[19]进行实验验证并与iLRAD算法进行对比。

1幂律分布模型

1.1节点数与边数的分布模型

社交网络、Internet等典型网络中，网络节点数多，节点之间通联规模大。已有研究表明，复杂网络中节点数与边数之间的关系服从幂律分布模型[20]，即：

其中，c,α均为常数，两边取对数得到：

logE(t)=a0logN(t)+b0

从而可以进行线性回归分析对复杂网络进行建模。另一方面，复杂网络的度数分布满足幂律(power law)[21]：

p(x=k)=cx-γ

文献[22]给出了复杂网络在允许节点自连接和节点间多次连接时的幂律分布推导。文献[23]给出了复杂网络在不允许节点之间只能单连接情况下幂律分布的推导。因此，可以根据复杂网络中节点数与边数的分布关系，判断网络是否异常。

1.2节点数与通联累积量的分布模型

文献[17]中提出iLRAD方法，该方法利用回归模型，将网络的节点个数，边的个数以及节点的度等参数作为衡量网络异常的指标。已有研究指出网络中节点和边的个数满足幂律分布，在做适当变换后，可以利用线性回归对两个参数进行回归分析。而实际网络数据中，对于通联关系，两个节点可能会在短时间内频繁通信，该频繁通信可能代表着网络异常，例如网络遭受ARP攻击后，一些节点会频繁向其他节点发送数据请求通信，而上面的iLRAD方法对于发生在同一个窗口内的频繁通信事件仅作一次统计，可能对丢失两点之间频繁通信导致的异常现象的漏警。

为了针对异常的高频次通联行为进行检测，本文在iLRAD基础上提出cLRAD方法，即对于网络通信，对一段时间窗口内的节点之间的通信次数进行累加，作为通联累积量。可以证明，通联累积量与节点仍然满足幂律分布关系。采用相同的方法可以对频繁发生通信的异常事件进行检测。

对于具有N个节点的复杂网络，假设任意两个节点之间产生通联的概率为p，并且两个节点之间可以产生多次通联，则任意两个节点之间通联累积量的期望值为：

因此对于N个节点的网络具有的通联累积量之和的期望值为：

对于复杂网络，节点个数一般较大，因此可以认为E～cNα，即复杂网络的通联次数与节点数在取对数后仍然满足线性关系。因此可以采用线性回归的方法计算系统模型，从而找出距离模型较远的异常点。

2基于通联累积量的动态网络异常检测算法(cLRAD)

2.1cLRAD算法原理

cLRAD与iLRAD算法的基本原理大致相同，iLRAD是对网络中节点之间的通联关系和节点数进行回归建模，而cLRAD则是对通联累积量与节点数的关系进行建模。cLRAD算法首先统计各个时间窗内网络的通联累积量，对通联累积量和节点数取对数后进行线性回归，记通联累积量取对数后的序列为{y1,y2,…yn}，节点数取对数后的序列为{x1,x2,…xn}，则线行回归计算如下：

2.2针对小规模网络状态的考虑

对于上面的幂律分布律，在网络中节点数较多时可以较好的满足，而在节点数较少时，网络的通联累积量并不能很好的满足上面的统计规律，数据分散性较大，采用此时的数据进行回归分析是不合适的。本文提出结合网络总体规模判断当节点数较少时对网络数据截断，不作为模型的回归数据。

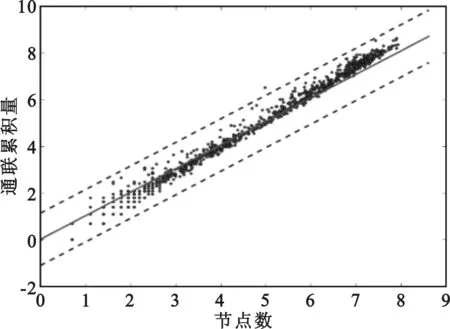
如图1所示，采用的是enron数据库，模型较好的满足线性关系，在回归分析时，由于小规模数据不能很好满足统计特性，该部分数据对回归结果影响较大，可以看出模型在网络大规模时具有一定的偏离。

图1　LRAD算法回归性质及截断数据示意

在采用iLRAD算法进行回归分析时，由于网络规模较大时的数据点被判定为异常点，在迭代过程中逐渐被删除，删除后会导致回归直线进一步偏离，最终导致回归直线偏离较远。

本文提出的小规模网络节点删除策略如下：由用户指定一个网络规模的最小值，主要为网络中通联累积量的大小，遍历所有时段内的网络，将满足该通联累积量的最小节点个数以及最多节点个数的均值作为门限，在回归分析时，不考虑节点数小于该门限的网络，对所有超出门限节点数的网络进行回归分析。设计该截断小规模网络策略的原因主要是为了解决图1所示的情况回归偏离的情况，该截断方法可以有效避免小规模网络数据点离散较大的现象，只保留虚线右上角区域的稠密数据点。截断数据的截断阈值选择如下：

输入，网络规模的最小边数e_min

输出，网络规模的点数阈值n_threshold

forGin {G1,G2,…GM}:

if e_min≤G.number_of_edges

n_list.append(G.number_of_nodes)

nγ= 0.5(max(n_list)+min(n_list))

2.3针对重点节点对的考虑

在复杂网络中，某两对节点之间的通信可能是非常重要的，当某两个节点之间发生通联时，其对应异常的可能性比较大，此时需要对节点对之间的通信情况进行加权。对于重要的节点，采用权值高来表示其相应的重要程度，一旦发生通联则引起异常的可能性大。然而，网络的权重会影响幂律分布，从而导致回归模型不准确，因此需要尽量少的设置加权边，使其对整体统计量影响不会很大。

2.4cLRAD算法流程

在LRAD算法的基础上，考虑网络中节点频繁通信的异常检测问题，结合实际数据特点，设定数据截断阈值并预置重要节点，相应的cLRAD算法流程如下所示：

输入：业务通联事件序列{(S0,D0)|t0,(S1,D1)|t1,…,(SN,DN)|tN}，窗口长度，节点之间通信的重要程度

输出：异常时间段

1)按照窗口长度，划分通联事件序列。

根据窗口长度划分时间段分段点{T0,T1,…TM}

fortin {t0,t1,…tN}:

ifTi≤t

Gi.add_edges(Si,Di)

2)统计各个时段内网络中节点个数以及通联次数，当遇到重要节点之间通信时，需要考虑节点的权值。

node_list.append(G.number_of_nodes())

for (u,v) inG.edges():

edge_count+=G(u,v) *weight(u,v)

edge_list.append(edge_count)

3)对node_list和edge_list中的数据取对数。

log_n = log(node_list)

log_e = log(edge_list)

4)截断较小规模的网络数据。

for (n,e) in zip(log_n, log_e):

ifn>nγ:

part_log_n.append(n)

part_log_e.append(e)

5)对part_log_n和part_log_e进行线性回归。

6)计算不符合回归直线的点标记为异常点。

for (i, (n,e)) in enumerate(zip(log_n, log_e)):

anomalous.append(i)

返回:anomalous

输入为各个时刻的通联数据，首先根据窗口将数据划分到各个时段，时段内的通联关系构成网络，当节点对之间存在多次通联时，需要考虑节点重要程度加权处理通联累积量。然后对各个时段的网络节点和通联累积量取对数，截断较小规模网络数据，进行线行回归。将各个时段的数据点带入回归直线，偏离回归直线超过回归偏差的数据所对应的时间段标记为异常时间段。

3实验结果

采用Enron语料库作为数据对象，挖掘其中的异常结果。Enron语料库是Enron公司公开的数据库，包含158个用户在1979年12月31日到2001年7月12日之间发送的619,446条邮件信息。本文的仿真实验将时间段设定为一天。

在不截断小规模数据情况下，cLRAD异常检测算法结果如图2所示，有个别节点可以被判定出是异常节点。说明这些节点在一天之内发生了频繁通信，该现象与网络受到攻击类似，而LRAD算法不能检测出该异常。

下面人为地加入通信异常，查看异常检测结果。对节点schottla@us.cibc.com和deborahlowe@akllp.com的通信人为增加20%，可以认为增加的这部分通信是异常，进行异常检测的结果如图3所示。

图2节点数与通联累积量的回归关系

可以看出，在节点之间通信数量发生变化时，cLRAD算法可以较好的检测出网络异常，而LRAD方法对于两节点之间的频繁通信只做一次记录，因此LRAD方法对此类异常无反应。

图3　人为增加通联次数的异常检测效果

设置表2中所示节点对之间的通信作为重点监控对象，当表中节点之间发生通信时，认为异常情况较为严重，实验结果如图4所示。

表2　通信节点对和权值对应关系

图4加权通信后的网络异常检测效果

对于权值较大的节点对之间的通信，其偏离系统回归模型较远，cLRAD算法可以较好的检测出此类异常。而LRAD对待所有通联行为是等同处理的，因此不能处理该类特殊通联问题的情况。

将规模小的数据进行截断，选取数据在最大通联数的20%以下的网络规模被截断，此时的网络回归模型如图5所示。可以看出，与图2相比，此时回归直线能够较好的表征网络节点和通联次数之间的变化关系，回归直线在分布密集的数据中。

图5　截断数据异常检测结果

如图5所示，截断小规模网络数据的回归效果更加接近网络模型，回归直线没有偏离数据集中区域，网络异常检测结果更加准确。然而如何选择阶段阈值是一个需要继续研究的问题。

上面的实验中，对数据的预处理是将1天内的数据作为一个通联网络进行异常检测的，检测结果以天数为粒度，还可以以周为单位，进行异常检测，而此时的检测结果表明，有些异常可能发生漏警。由于本算法采用的线性回归方法计算复杂度低，计算速度块，因此，在实际处理问题时，可以遍历不同时窗粒度，给出多粒度异常检测结果。

实验结果表明，cLRAD算法可以找出网络拓扑结构发生异常的情况，并且在用户指定某些特殊节点通联的情况下可以灵敏的找出网络中的异常。然而，该方法需要进一步完善时间窗口长度以及截断数据阈值的选择问题。

4结语

本文针对LRAD算法对于节点多次通联的异常现象无法检测的缺点，提出了cLRAD算法。首先给出了通联累积量的定义并证明其满足幂律分布规律，然后提出了利用该规律进行回归建模方法。在回归分析中，针对网络规模较小时网络数据分散，不能得到较好的回归模型的问题，提出筛选网络数据的策略，然后根据实际中存在的某些节点需要重点关注的场景，提出了cLRAD算法对于特殊节点的处理方法。实验证明，cLRAD对于网络中存在多次通联的异常具有较好的检测效果，而LRAD不能检测出该类异常。

参考文献：

[1]文拯, 梁建武, 陈英. 关联规则算法的研究[J]. 计算机技术与发展, 2009, 5 (19):56-58.

WEN Zheng, LIANG Jian-wu, CHEN Ying. Research of Association Rules Algorithm[J].Computer Technology and Development, 2009,5(19):56-58.

[2]Varun Chandola, Arindam Banerjee, and Vipin Kumar. Anomaly Detection: A Survey[J]. ACM Computing Surveys, 2009, 41(3).

[3]CHENG Hai-bin,TAN Pan-ning, et al. Detection and Characterization of Anomalies Multivariate Time Series[C].SDM, 2009.

[4]LI X, LI Z, HAN J, et al. Temporal Outlier Detection in Vehicle Traffic Data[C]//Proceedings of the 25thInternational Conference on Data Engineering (ICDE2009). IEEE Computer Society, 2009:1319-1322.

[5]Breunig M, Kregel H, Ng R, et al. LOF: Identifying Density-based Local Outliers[J]. ACM SIGMOD Record, 2000, 29(2):104.

[6]LAI K,King G,Lau O. Arima: Arima Models for Time Series Data, 2007.

[7]DING Hui, Goce Trajcevski, etc. Querying and Mining of Time Series Data: Experimental Comparison of Representations and Distance Measures[C]. VLDB,2008.

[8]YANG Ki-yong and Cyrus Shahabi. A PCA-based Similarity Measure for Multivarite Time Series[C]. MMDB,2004.

[9]WENG Xiao-qing, SHEN Jun-yi. Outlier Mining for Multivariate Time Series based on Local Sparsity Coefficient[C]. Proceedings of the 6thWorld Congress on Intelligent Control and Automation, 2006.

[10]陈湘涛，李明亮，陈玉娟.基于时间序列相似性聚类的应用研究综述[J].计算机工程与设计，2010，31(03):577-581.

CHEN Xiang-tao, LI Ming-liang, CHEN Yu-juan. Summaly of Application Research based on Clustering of Time Series Similarity[J]. Computer Engineering and Design, 2010,31(03):577-581.

[11]Erdos P, Renyi A. On the Evolution of Random Graphs[J]. Pub1. Math.Inst.Hung.Acad.Sci, 1960,5:17-16.

[12]Barabasi A, Albert R. Emergence of Scaling in Random Networks[J]. Science, 1999, 286(5439):509.

[13]Leskovec J, Kleinberg J, Faloutsos C. Graph over Time: Densification Laws, Shrinking Diameters and Possible Explanations[C]//Proceeding of the 11thACM SIGKDD International Conference on Knowledge Discovery in Data Mining(KDD’05). Chicago, Illinois, USA.: New York, USA, 2005:177-187.

[14]Bunke H,Dickinson P J, Kraetzl M, et al. A Graph-Theretic Approach to Enterprise Network Dynamics[M]. Birkhauser Boston, 2007.

[15]Lahiri M, Berger-Wolf T Y. Periodic Subgraph Mining in Dynamic Networks[J]. Knowlinf Syst. 2009,24(3):467-497.

[16]Berlingerio M, Bonchi F, Bringmann B, et al. Mining Graph Evolution Rules[C]//ECML/PKDD 2009. Springer Berlin Heidelberg, 2009:115-130.

[17]孟啸.动态复杂网络中的异常检测问题的研究[D]. 哈尔滨：哈尔滨工业大学计算机科学与技术学院,2010.

MENG Xiao. Research on Anomaly Detection in Dynamic Complex Networks[D]. School of Compter Science and Technology, Harbin Institute of Technology. 2010.

[18]李聪,宋路.浅谈IP RAN网络建设思路与策略[J].通信技术,2015,48(01):75-81.

LI Cong, SONG Lu. Idea and Strategy of IP RAN Network Development[J]. Communications Technology, 2015, 48(01): 78-81.

[19]Jitesh S, Jafar A. The Enron Email Dataset Database Schema and Brief Statistical Report. University of Southern California Los Angeles[R]. CA 2004.01.

[20]Dorogovtsev S N, Mendes J F F, Samukhin A N. Structrue of Growing Networks with Preferential Linking[J]. PRL, 2000, 85:4633-4636.

[21]Barabasi A,Albert R.Scale-Free Networks: A Decade and Beyond[J]. Science,2009,325.

[22]Bollobas B, Riordan O M, Spencer J,et al. Degree Sequence of a Scale-Free Random Graph Process[J]. Random Structures and Algorithm, 2001, 18:279-290.

[23]Holme P, Kim B J. Growing Scale-Free Networks with Tunable Clustering[J]. PRE,2002,65:026107.

贺亮(1990—),男,硕士研究生,主要研究方向为网络异常检测；

褚衍杰(1982—),男,工程师,主要研究方向为智能信息处理；

韩杰思(1981—),男,工程师,主要研究方向为图像处理，网络异常检测。

Anomaly Detection Algorithm based on Communicating

Cumulant in Dynamic Network

HE Liang，CHU Yan-jie，HAN Jie-si

(State Key Laboratory of Science and Technology on Blind Signal Processing, Chengdu Sichuan 610041,China)

Abstract：In network operation and maintenance fields, one of the biggest concerns is how to detect the network anomaly without delay. Aiming at the problem that the existing methods could hardly detect the anomaly in case of high-frequency communication, an anomaly detection method based on statistic model for high-frequency communication is proposed. In this method,the power-law distribution model is used to describe the relation of between the number of nodes and frequency communicating cumulant,this model is matched via linear regression,and the network state with regression error beyond the confidence coefficient is predicated as abnormal. In addition,for the heavy-concerned node pair in the network,a predistribution scheme of its weight assignment is given. However, in light of small-scale network status, which could not completely follow power-law distribution, a sample pre-selection strategy is suggested,so as to reduce the false alarm of abnormal behavior. Finally, experiment results indicate that the proposed method is of fairly high detection rate both in abnormal high-frequency and low-frequency communication.

Key words：dynamic complex networks; anomaly detection; communication cumulant; linear regression

作者简介：

中图分类号：TN 911

文献标志码：A

文章编号：1002-0802(2015)12-1400-06

收稿日期：2015-07-08；修回日期：2015-10-20Received date:2015-07-08；Revised date：2015-10-20

doi:10.3969/j.issn.1002-0802.2015.12.016