SOQPSK信号位定时与载波联合估计算法

贾　鹏，唐　远，黄　尧

(1.国家移动卫星通信工程技术研究中心,江苏 南京 210002;

2.解放军理工大学 通信工程学院,江苏 南京 210007)



SOQPSK信号位定时与载波联合估计算法

贾鹏1，唐远2，黄尧2

(1.国家移动卫星通信工程技术研究中心,江苏 南京 210002;

2.解放军理工大学 通信工程学院,江苏 南京 210007)

摘要：针对在极低信噪比、大多普勒频偏环境，研究了SOQPSK信号的位定时、载波频率和相位联合估计算法。该算法运用了Laurent分解原理以减少匹配滤波器个数，位同步信息的提取与接收译码均可共用前端的匹配滤波器，进一步降低接收端复杂度。同时，该算法的同步信息的提取方法也是低复杂度的。计算机仿真结果表明，该算法能够在低信噪比、大频偏条件下，以较低的低复杂度实现同步信息提取，且同步性能良好。

关键词：SOQPSK；Laurent分解；位定时估计；载波估计

0引言

SOQPSK作为一种高效率的恒包络连续相位调制方式，其相位轨迹没有跳变，抗非线性能力较强且通过选用适当的频率整形脉冲，可以使其频谱特性大大改善，与其它调制方式相比，SOQPSK的上述特性使得它具有显著的优点，非常适合于深空通信[1]。

深空通信系统往往工作在极低信噪比和大多普勒频移环境下，此时位同步和载波同步变得更加困难。目前，关于SOQPSK信号同步算法研究的文献并不多，很多时候，基于CPM信号在包络恒定等方面与SOQPSK信号的相似性，可以考虑将CPM信号同步算法扩展到SOQPSK信号。

文献[2]中对非线性变换的滤波法、同相正交环、逆调制环和判决反馈环四种载波同步方法进行了描述，分析了它们的工作原理， 讨论了载波同步的性能指标。文献[3]提出了一种基于NDA(非数据辅助)的联合定时频率估计，但是只适用于MSK和GMSK信号。文献[4]所提种基于DA(数据辅助)的联合同步主要针对突发CPM信号。文献[5]所提定时、频率、相位联合估计分支度量不是基于Laurent分解的，计算复杂。文献[6]联合载波相位和位定时估计的算法基于前向反馈结构，性能不佳。文献[7]的定时-相位联合估计算，需数据采样较密集时才能得到好的估计性能，数据量大且计算复杂。

文中提出一种适用于SOQPSK 信号基于Laurent 分解的低复杂度定时载波联合估计算法，给出联合估计算法的实现方案，通过仿真分析该算法的性能及优缺点。

1SOQPSK信号模型

SOQPSK可以描述为复基带形式的CPM信号：

(1)

式中，Es是符号能量，T是符号周期。相位轨迹函数为：

(2)

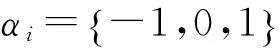
(3)

式中，整形脉冲函数f(t)持续时间为L个符号周期，最大取值为1/2。如果L=1，称为全响应，如果L>1，则称为部分响应。

根据整形脉冲函数f(t)的不同，SOQPSK有不同的形式，其中比较常见的有SOQPSK-MIL、SOQPSK-TG等。其中，整形脉冲函数为L=8的部分响应：

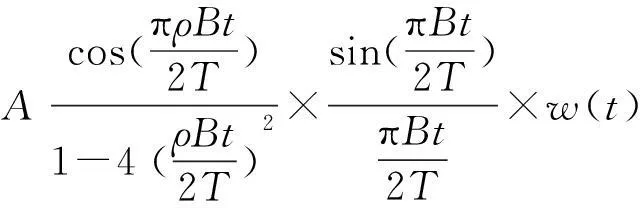
(4)

式中，窗函数w(t)表达式为：

式中，A的取值使fTG(t)的最大取值为1/2，T1=1.5，T2=0.5，ρ=0.7，B=1.25。

2基于Laurent分解的低复杂度联合估计算法

SOQPSK可以看成是一种特殊的三进制CPM信号，三进制CPM信号通过映射可表示为多个二进制CPM信号的乘积，对各个二进制CPM信号分别进行Laurent分解，然后合成简化。复基带形式的三进制CPM的表达式为：

(5)

式中，调制指数h=1/2，发送信号αi={0,±2}，q(t)是有限长函数f(t)的积分。 将三进制CPM信号分解为PAM信号的关键是将三进制信号表达为：

αi=γ1,i+γ0,i

(6)

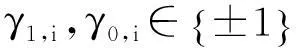
s(t;α)=sbin(t;γ1)sbin(t;γ0)

(7)

将式(7)代入二进制CPM 的PAM信号表达式，则三进制CPM信号可以表示为:

(8)

式中：

(9)

这种表达仍比较复杂，需进一步简化。最终得到：

(10)

式中伪符号集νl,n表示为：

(11)

同时，脉冲分量ρl(t)表示为：

(12)

经过Laurent分解所得脉冲分量ρl(t)有着不同的幅值、周期长度和能量，其中p0(t)幅值最大、持续时间最长，且包含了信号的绝大部分能量。因此，在很多实用场合，CPM信号都以ρl(t)的前几项进行近似。

在观察区间0≤t≤L0T上，SOQPSK信号最大似然估计的似然函数可以表示为：

(13)

在Viterbi译码的过程中，保存每一个状态下的最大路径度量值，接收端的度量增量为：

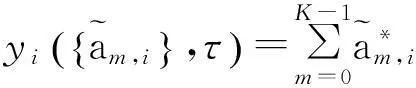
(14)

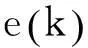
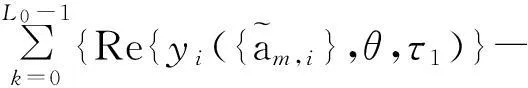
在定时误差得到初步校正的时候，提取载波相位误差函数为：

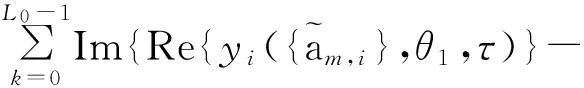
整个算法数字实现框图如图1所示：接收端接收到信号以后将其送入滤波器组，然后运用Viterbi算法得到分支度量值。从分支度量值里提取定时和相位误差，并分别将定时和载波相位偏差进行反馈。

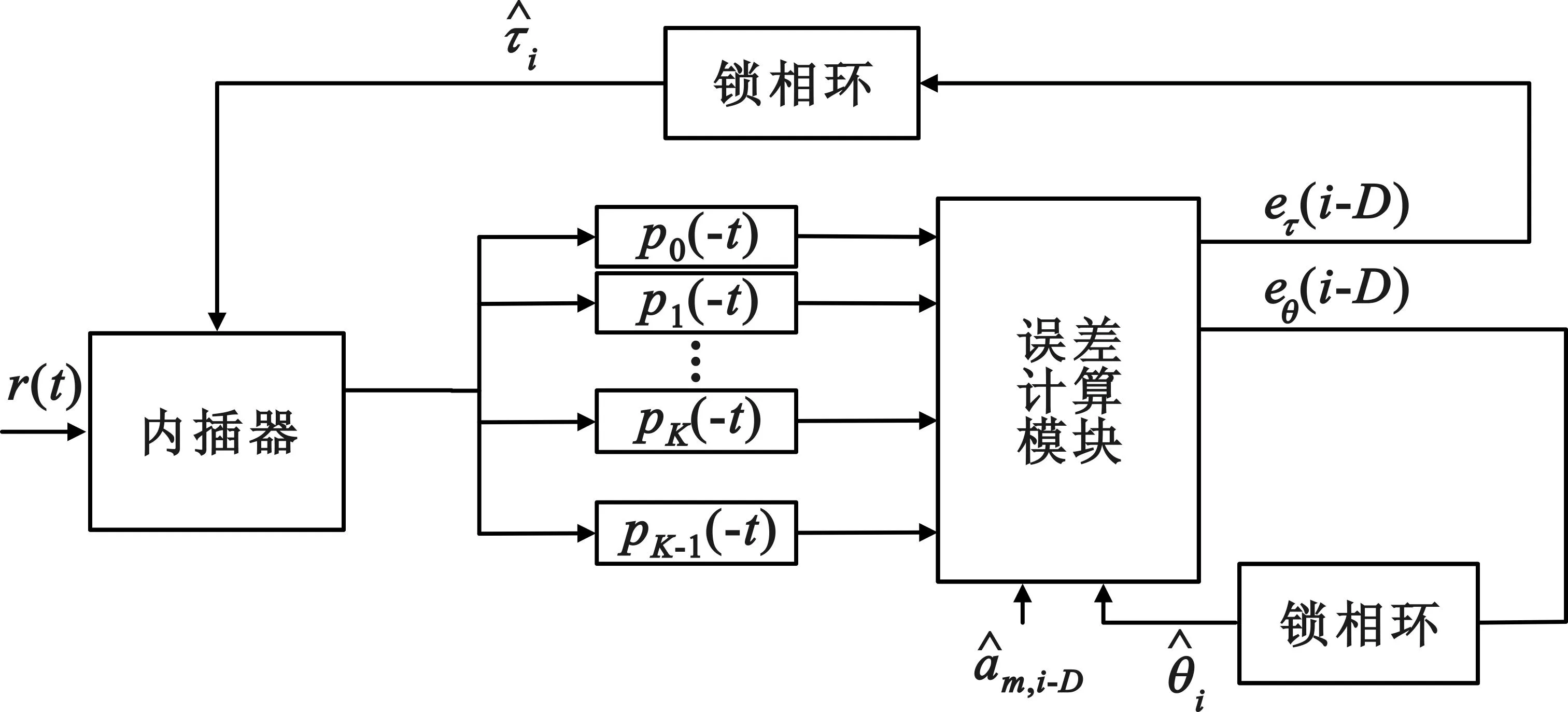
图1　基于Laurent分解的低复杂度联合估计

在整个实现过程中，该算法有两处处理是简化的。其一是基于Laurent分解的匹配滤波器的个数大大减少，且可以与符号检测共用；其二是误差信息的提取相对简化，尤其在与文献[7-8]比较时，实现复杂度大大降低。

3计算机仿真

在高斯白噪声信道中，假设在考虑存在位定时误差、相位误差和频偏的前提下，接收端的信号可以表示为：

r(t)=s(t-τ;α)ej(2πvt+θ)+n(t)

(15)

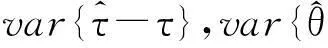
通过仿真,得到无噪声情况下不同初始相偏大小θ下SOQPSK-TG信号的定时误差曲线如图2所示。从图2中可以看出，在没有加入相偏时，SOQPSK-TG信号的定时误差变化最明显。在加入pi/8和pi/16的固定相偏以后，定时误差变化明显减弱，在不同相偏对其影响并不明显。这是因为此时定时信息提取于最大路径度量值的实部，虚部(即相位)的影响并不明显。

图2　不同固定相偏下算法的定时S曲线

进行更进一步的仿真，固定初始相偏θ为pi/16,改变频偏大小ν，得到不同噪声条件下的定时误差和相位误差曲线如图3和图4所示。由图可知，随着频偏的减小，误差曲线幅度变化越明显，相位S曲线越平滑。也就是说，随着频偏的增加，估计性能会变差。

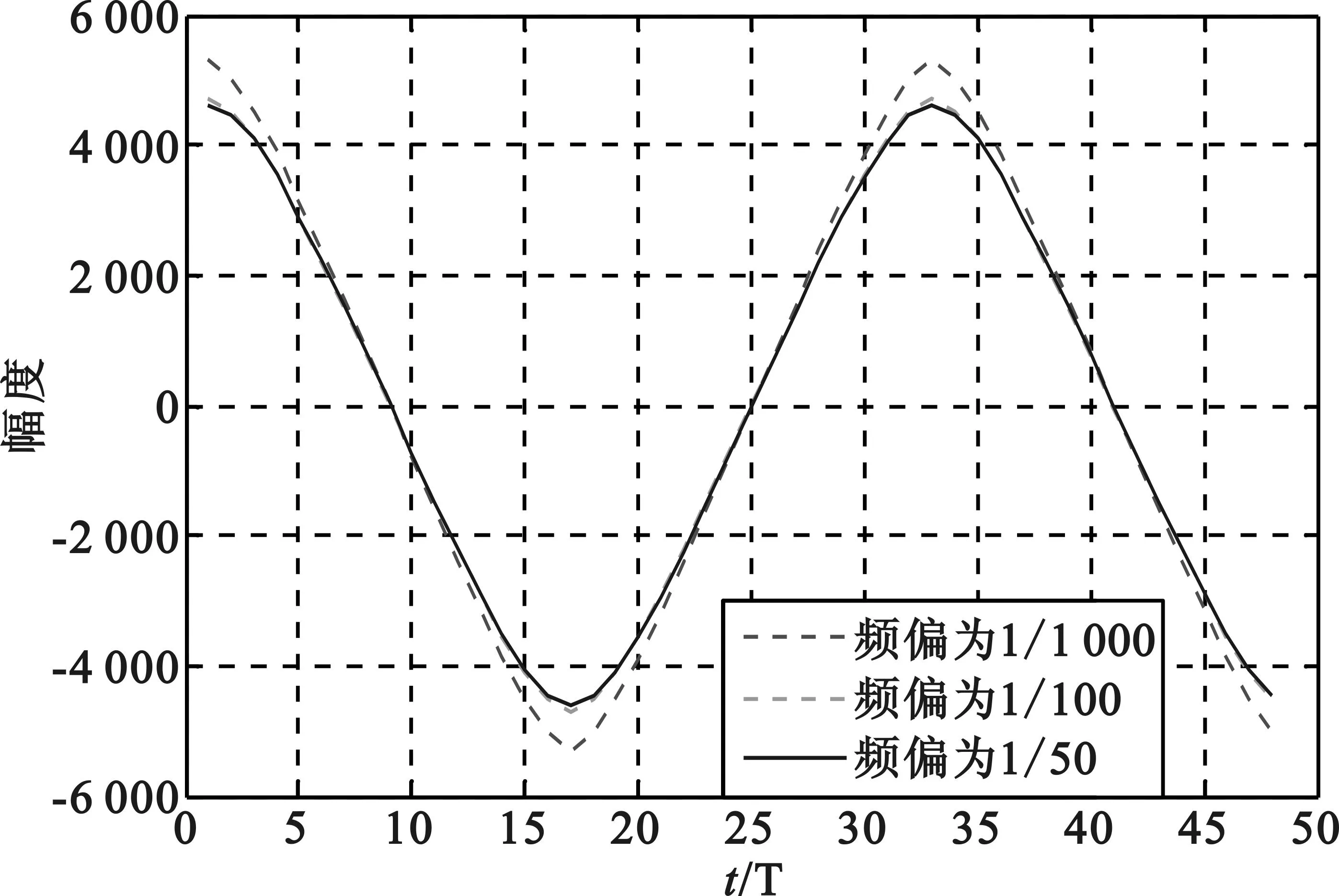
图3不同频偏下算法的定时S曲线

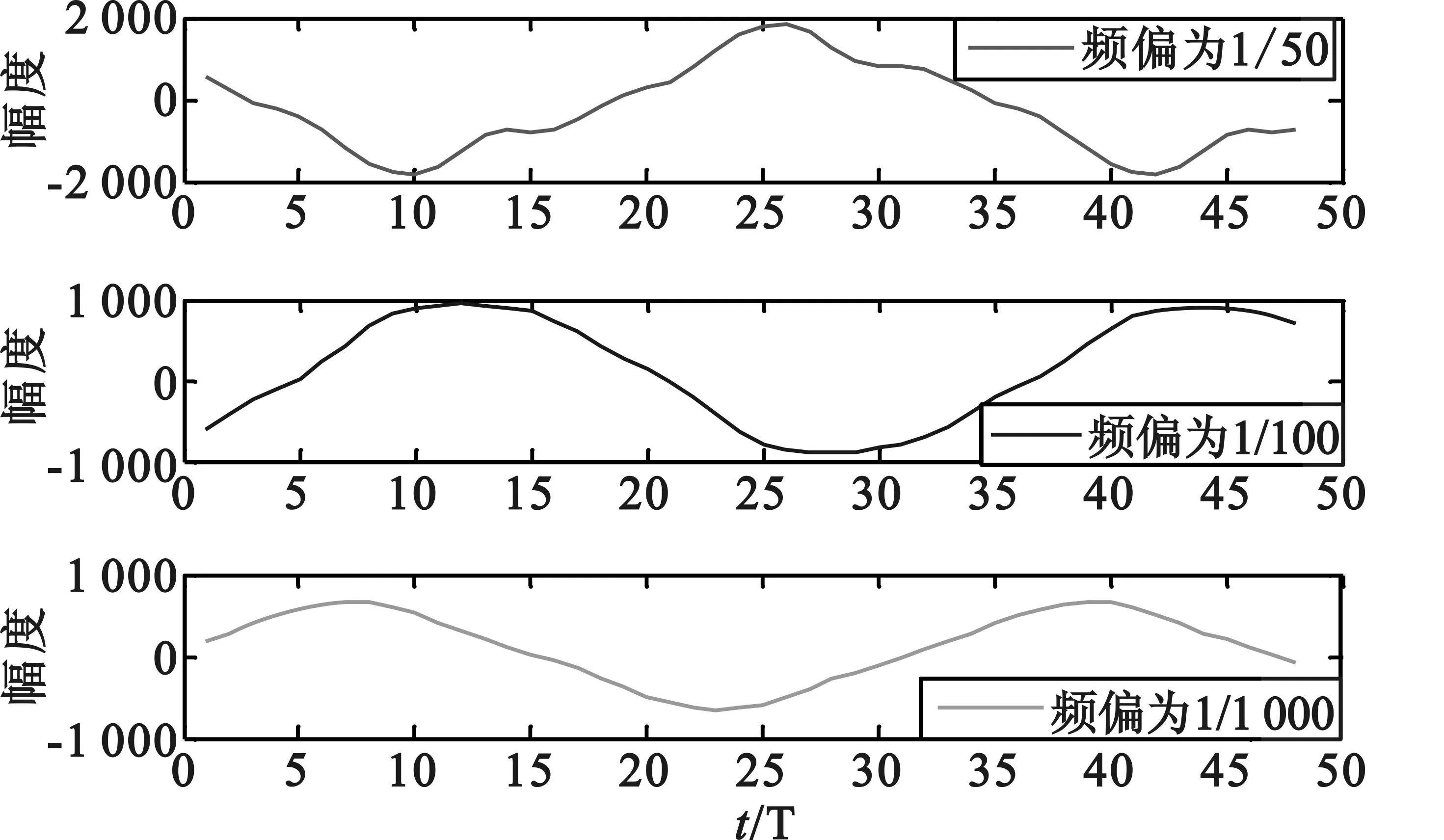
图4　不同频偏下算法的相位S曲线

图5表示该算法的定时性能，横轴表示不同大小的符号信噪比Eb/N0，纵轴表示定时同步信息的归一化均方误差。此时取初始相偏θ为pi/16,频偏大小ν为1/100，由图5可知，对于SOQPSK-TG信号，定时估计的标准差在 10-2到10-3数量级之间，基本满足工程实现需要，但是与文献[8]所示算法以及MCRB界相比还有一定的差距。

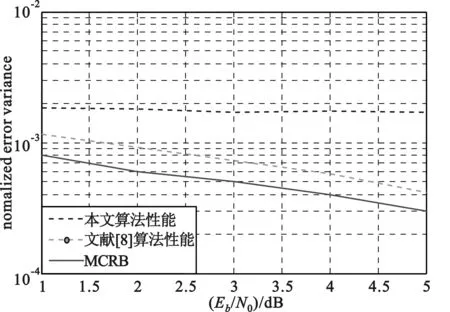
图5　该算法的定时性能曲线

比较本文与文献[7-8]所示算法的优缺点，由表 1可知，本文算法的优势在于实现方案更为简单，计算复杂度小，同步实现快速准确，易于数字实现，虽然牺牲了一定的估计性能，却有效降低了系统的复杂度，简单实用。

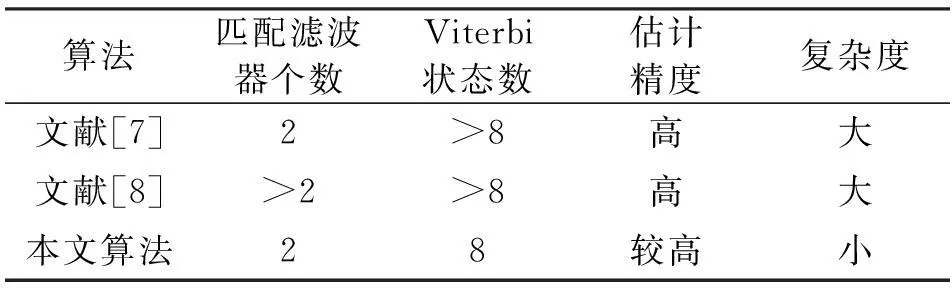
表1　SOQPSK-TG信号的三种联合算法的比较

4结语

SOQPSK信号的恒包络特性使其特别适用于深空通信，此时往往工作在极低信噪比和大多普勒频移环境下。针对位定时与载波估计问题，本文提出了一种SOQPSK信号的联合同步方案，该方案采用Laurent 分解对信号进行简化，在此基础上运用Viterbi算法得到分支度量值，并从分支度量值里提取定时和相位误差。该方案的主要优点有：估计性能良好，定时同步独立于相位同步，位定时同步能够适用于相干接收机和非相干接收机，前端匹配滤波和定时信息的提取运算量大大减小的，且能够作用于低信噪比和大频偏环境。

参考文献：

[1]Simon M. Bandwidth-Efficient Digital Modulation with Application to Deep-Space Communication[D]. Wiley, New York, 2003.

[2]王钢,刘毅鹏.BPSK 载波同步技术的研究[J].通信技术, 2003(01):21-33.

WANG Gang. LIU Yi-peng. Research on Carrier Synchronization Technique in BPSK[J]. Communications Technology. 2003, (01): 21-33

[3]Morelli M, Mengali U. Joint Frequency and Timing Recovery for MSK-Type Modulation [J]. IEEE Transactions on Communications, 1999, 47(6): 938-946.

[4]Hosseini E and Perrins E. Training Sequence Design for Data-Aided Synchronization of Burst-Mode CPM. Global Communications Conference(Globecom), 2012 IEEE. 2012. Anaheim, CA.

[5]Morelli M, Mengali U and Vitetta G M, Joint Phase and Timing Recovery with CPM Signals. Communications, IEEE Transactions on, 1997,45(7):867-876.

[6]D'Amico A A. Feedforward Joint Clock and Phase Estimation Schemes for SOQPSK-Type Signals. Wireless Communications Letters, IEEE, 2013,2(6):679-682.

[7]刘晓明,汪梦柔,吴皓威等.SOQPSK信号的定时-相位联合估计算法[J].江苏大学学报，2011(32):443-448.

LIU Xiao-ming, WANG Meng-rou, WU Hao-wei, et al. Joint Timing and Phase Estimation Algorithm for SOQPSK Signals[J].Journal of Jiangsu University (Natural Science Edition)，2011(32):443-448.

[8]王永刚.连续相位信号低复杂度同步与均衡技术研究[D].南京:解放军理工大学,2013.

WANG Yong-gang. Study on Low-Complexity Synchronization and Equalization Technology of Continuous Phase Signal [D] Nanjing: PLA University of Science and Technology,2013.

贾鹏(1973—)，男，博士，高工，主要研究方向为卫星通信；

唐远(1991—)，男，硕士研究生，主要研究方向为卫星通信与移动通信；

黄尧(1989—)，女，硕士，主要研究方向为卫星通信。

SOQPSK Timing Signal and Carrier Joint Estimation Algorithm

JIA Peng1，TANG Yuan2，HUANG Yao2

(1.National Mobile Satellite Communication Engineering Technology Research Center, Nanjing Jiangsu 210002, China;

2.Institute of Communications Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007, China)

Abstract：Aiming at the environment with very low signal-to-noise ratio and big Doppler frequency offset, the bit timing, carrier frequency and phase joint estimation algorithm of SOQPSK signal are discussed in this paper. Laurent decomposition principle is used in the estimation algorithm for reducing the number of matched filters, and both the extraction of bit synchronous information and the receiving decode could commonly share the front-end matching filters,thus to further decrease the receiver complexity. Additionally, the synchronous information extraction method of this algorithm is also of low complexity. Simulation results show that this algorithm could implement the extraction of synchronization information under the condition of low SNR and large frequency with a relatively low complexity, and also maintain a fairly good performance.

Key words：SOQPSK; Laurent decomposition;bit timing estimation; carrier estimation

作者简介：

中图分类号：TN911.3

文献标志码：A

文章编号：1002-0802(2015)12-1339-04

收稿日期：2015-07-16；修回日期：2015-10-29Received date:2015-07-16；Revised date：2015-10-29

doi:10.3969/j.issn.1002-0802.2015.12.004