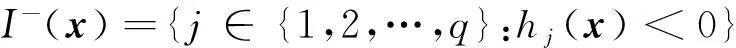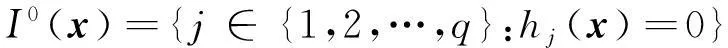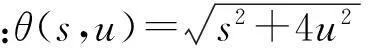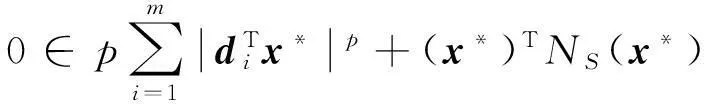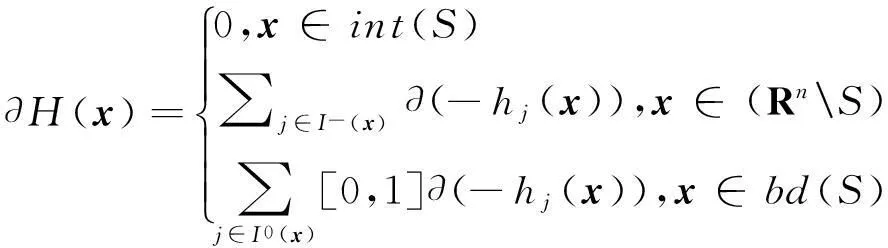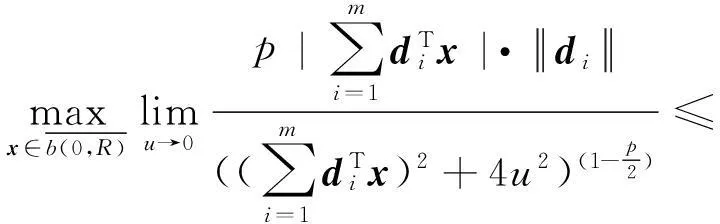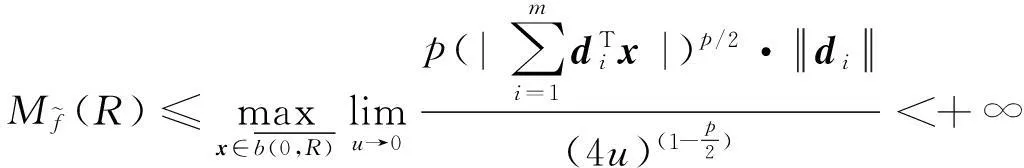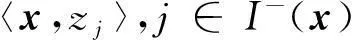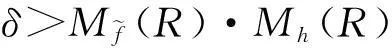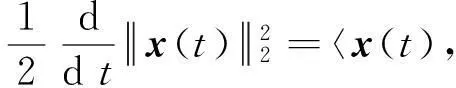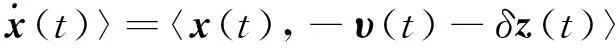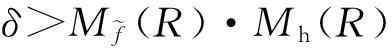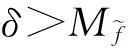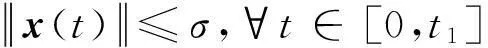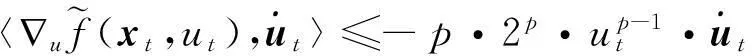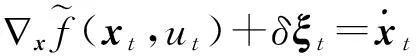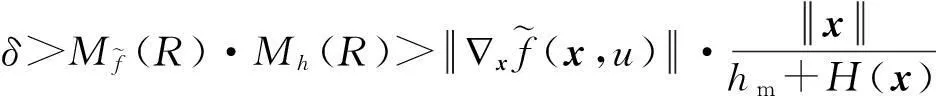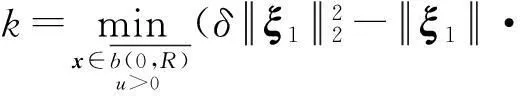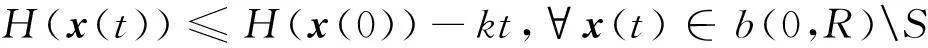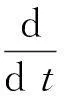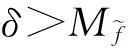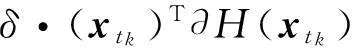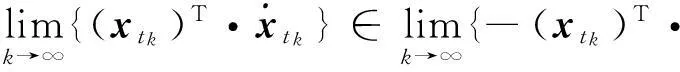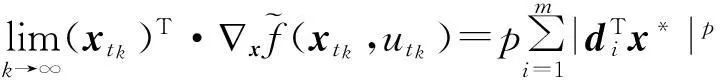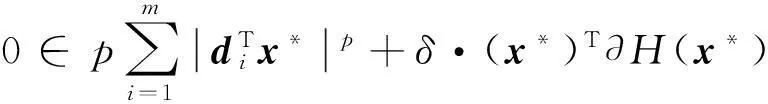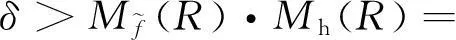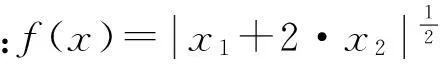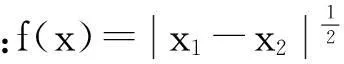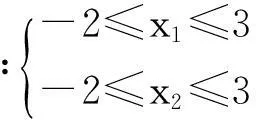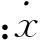光滑神经网络解决非李普西茨优化问题的研究*



光滑神经网络解决非李普西茨优化问题的研究*

通信地址：530004 广西南宁市广西大学计算机与电子信息学院Address:School of Computer & Electronics and Information,Guangxi University,Nanning 530004,Guangxi,P.R.China

喻昕,谢缅,李晨宇

(广西大学计算机与电子信息学院，广西 南宁 530004)

摘要：为寻求满足约束条件的优化问题的最优解，针对目标函数是非李普西茨函数，可行域由线性不等式或非线性不等式约束函数组成的区域的优化问题，构造了一种光滑神经网络模型。此模型通过引进光滑逼近技术将目标函数由非光滑函数转换成相应的光滑函数以及结合惩罚函数方法所构造而成。通过详细的理论分析证明了不论初始点在可行域内还是在可行域外，光滑神经网络的解都具有一致有界性和全局性，以及光滑神经网络的任意聚点都是原始优化问题的稳定点等结论。最后通过几个简单的仿真实验证明了理论的正确性。

关键词：非李普西茨函数；光滑逼近技术；稳定点；聚点

1引言

在科学和技术领域中，如最优控制、信号处理以及模式识别等应用经常会遇到优化问题。传统上一般采用数值计算的方法来解决线性或非线性规划问题，例如牛顿梯度法、罚函数法等等。很多工程应用往往需要得到优化问题的实时解。然而传统的数值方法往往无法满足实时的要求，因为它计算解的时间依赖于问题的维数与结构以及算法的复杂度。求解优化问题实时解的一个可行且很理想的方法就是应用人工神经网络。基于模拟电路的神经网络，由于其内在的大规模并行运算和快速收敛性，可用它进行优化问题的实时求解[1]。

近年来用神经网络来解决非线性规划问题已经得到了很大的发展，并取得了很好的应用。在1986年，TankDW和HopfieldIJ[2]应用Hopfield神经网络模型方法解决了线性规划问题。在1988年，KennedyM和ChuaL[3]提出了解决非线性规划问题的动态规格非线性规划单元NPC(NonlinearProgrammingCircuit)模型，该神经网络模型采用惩罚函数方法来估算最优解。此后，用来解决最优化问题的神经网络模型层出不穷，比如基于拉格朗日方法的拉格朗日神经网络模型[4,5]、基于投影方法的投影神经网络模型[6]、用来解决非光滑非凸或凸问题的单层递归神经网络模型[7,8]。

然而，从上述所提到的神经网络模型文献中，可以发现它们都有一个显著的相似点，就是它们所要求的目标函数必须要满足李普西茨条件，但是在许多重要的应用中，比如图像修复、信号重建以及变量选取等应用中，最优化问题并不满足李普西茨条件，那么对于这样的问题，上述文献所提到的神经网络模型则不能解决。

最近几十年，人们发现光滑逼近技术能够解决目标函数是一般非光滑(满足李普西茨条件)非凸甚至不满足李普西茨条件的优化问题。光滑逼近技术是针对具有特殊结构的一类目标函数，这类目标函数可能是一般非光滑、非凸甚至是非李普西茨函数，通过将目标函数与光滑函数结合来形成具有光滑性质的新目标函数[9]。文献[10]采用投影方法与光滑技术结合构造了光滑神经网络模型，解决了原始优化问题的目标函数是非李普西茨函数的问题，但是在此文献中约束条件为非函数定义的凸性区域，因此在某些情况下进行投影计算是困难的。在文献[11]中，广义动态规格非线性规划单元G-NPC(GeneralizedNPC)模型被提出,它可以解决非光滑非线性优化问题，此模型采用惩罚函数方法来求解原始问题的最优解。然而，此模型要求目标函数必须满足李普西茨条件。鉴于文献[10]和文献[11]中出现的不足，本文提出一类新的解决优化问题的神经网络，其限制条件为不等式区域，与文献[10]相比不需进行投影计算。此外，问题的目标函数可以是非李普西茨函数，克服了文献[11]中要求目标函数须满足李普西茨条件的不足。

本论文的结构组织如下：第1节详细地描述了在本论文将出现的相关符号、定义以及要解决的优化问题；第2节提出光滑神经网络模型；第3节对光滑神经网络能够解决原始优化问题做了充分的理论分析；第4节提出两个仿真实验例子，证明了理论的有效性。

2预备工作

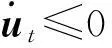
本部分主要对相关问题做一个简要的介绍，以及对相关概念、符号做一个简要的描述。本文要解决的最优化问题的描述如下：

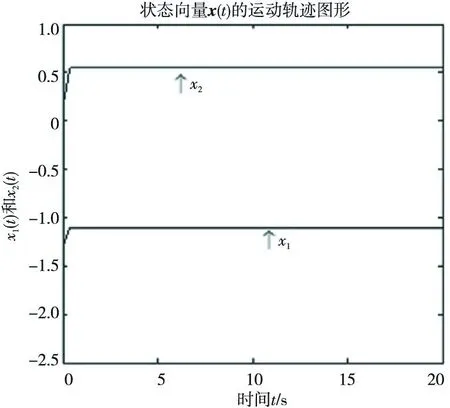
(1)

这里0

定义1如果存在正数κ和ε，使得对于任意x1，x2∈x+εb(0，1)，|f(x2)-f(x1)|≤κ‖x2-x1‖成立，那么函数f:Rn→R在x∈Rn处满足李普西茨条件，若f:Rn→R在其定义域内所有点都满足李普西茨条件，则函数f:Rn→R是局部李普希茨函数。

(2)

定义3对于x*∈S，如果x*满足:

(3)

则x*为式(1)所述优化问题的一个稳定点。

参考文献对于本文所提到的正则函数，绝对连续函数以及上半连续函可以[6,12,15]，在此不赘述。 附中文

3模型描述

为了解决式(1)所述优化问题，本文所提出的光滑神经网络的模型描述如下：

(4)

其中，惩罚因子δ>0,

假设1约束函数-hj(x):Rn→R，j=1，2,…,q是凸函数，且存在0∈int(S)，使得hj(0)>0，j=1，2,…,q。

引理1对于任意初始点x0∈b(0，R)，光滑神经网络至少存在满足式(4)的一个局部解。

证明因-hj(x)：Rn→R，j=1，2,…,q满足局部李普西茨条件，式(4)的右边是一个上半连续的极值映射函数，所以在[0，t1]内必存在局部解x(t)满足式(4)，其中x(0)=x0是其初始点，[0，t1]为最大时间间隔。

□

即:

(5)

(6)

(7)

4主要结果

这部分主要介绍光滑神经网络解的有界性、全局性、神经网络的聚点和稳定点的关系。在本文的主要理论证明中，我们将使用xt和ut来表示x(t)和u(t)。

证明因为-hj在Rn→R上是凸函数且hj(0)>0。那么对于任意x∈RnS，以下关系式成立：

其中zj∈∂(-hj(x))。

因为z∈∂H(x),

所以:

因此:

□

证明当x(t)∈b(0，R)S时，可知:

其中,υ(t)∈。

由引理2可知,

所以：

(8)

而

(9)

由式(8)和式(9)可得:

(10)

□

因为x(t)在局部解存在的最大时间间隔[0，t1]内一致有界，通过解的扩展性定理[14]可知光滑神经网络在[0，∞)内有解，即存在全局解。

□

证明

(11)

由式(2)可知:

(12)

(13)

由式(11)和式(13)可得:

(14)

(15)

因为f(xt)+δH(xt)是连续函数，由定理1和推论1可知x(t)∈b(0，R)，∀t∈[0，∞)，所以f(xt)+δH(xt)在xt∈b(0，R)上必有下界，结合式(15)可得:

(16)

□

证明根据H(x)的定义以及假设1，可知H(x)是正则函数。根据链式法则可得：

(17)

(18)

对式(18)从[0，t](t>0)上积分得：

因此，当t≥H(x(0))/k时，H(x(t))≤0。

□

证明因为xt在可行域b(0，R)上一致有界，所以xt至少存在一个聚点。如果x*是xt的一个聚点，则存在数列{tk}，当limk→∞tk=∞时，limk→∞xtk=x*，limk→∞utk=0。由定理3可知，x*∈S。

式(4)两边乘以x(tk)可变为:

(19)

对式(19)两边取极限:

(20)

(21)

如果xt有两个聚点x*和y*，则存在两个数列{tk}和{sk}使得limk→∞tk=limk→∞sk=∞，limk→∞xtk=x*，limk→∞xsk=y*。因为x(t)∈b(0，R)是连续有界函数，所以x*到y*之间必存在一条路径o(x*，y*)，使得o(x*，y*)上的所有点都是聚点,从而都是式(1)所述优化问题的稳定点，这与假定式(1)所有的稳定点是孤立点相矛盾。

□

5实验仿真结果

为了证明所提出神经网络模型及相关理论的有效性，用以下三个受限问题的仿真实验进行验证。仿真实验是在Matlab R2012a平台下进行的。实验1的最优化问题的目标函数是非李普西茨函数，可行域由线性不等式函数组成。实验2的最优化问题的目标函数是非李普西茨函数，可行域由线性不等式和非线性不等式函数组成。实验3主要是为了将本文和文献[10]进行比较，以证明在实验3满足文献[10]的目标函数和可行域的条件下，当实验3和实验1的初始点相同时，实验3依然能实现实验1的效果，即本文中所阐述的理论和文献[10]一样能找到最优点，只是本文和文献[10]相比，没有使用投影算子，减少了计算量。

实验1

可行域：h(x)=0.5x1-x2+4≥0

首先，确定球形区域b(0，R)中的R、惩罚因子δ以及连续单调函数u。根据可行域覆盖范围，R取值为8，连续单调递减函数为u=e-0.1·t-2。在本文所做的仿真实验中，当u<0.018时，程序停止运行。惩罚因子δ根据式(5)~式(7)估算：

这里δ取值15。

对于原始受限问题，在可行域范围内当x1=x2时目标函数取得最小值，此时的(x1，x2)T为原始优化问题的最优解。为了验证理论的正确性，我们任意取三个点(-6，5)T、(-3，4)T和(2，-4)T。图1表明这三个初始点分别收敛于以下可行域中的三个点(-1.325，-1.325)T、(0.2，0.2)T和(-1，-1)T。显然它们都是原始优化问题的最小值。

Figure 1　Move track of the state vector x(t)图1　状态向量x(t)的运动轨迹图

实验2

和实验1的实验步骤一样，这里R取值4，δ取值为15，对于初始点分三种情况进行举例说明：

(1)初始点(-3，-1)T在可行域外。从图2可以看到，当t>2s时，状态向量x(t)在可行域中且趋向稳定，程序结束时的值为(-0.752 5，0.376 3)T。从原始优化问题的目标函数中可以看出，当x1=-2·x2时，目标函数取得最优解，可知(-0.752 5，0.376 3)T非常接近原始优化问题的最优解。

Figure 2　Move track of the initial point (-3，-1)T图2　初始点为(-3，-1)T的运动轨迹图

(2)初始点(1，1.5)T在可行域内。从图3可以看到，当t>2s时，状态向量x(t)在可行域内且趋向稳定，程序结束时的值为(0.2，-0.1)T，显然是原始优化问题的最优解。

Figure 3　Move track of the initial point (1，1.5)T图3　初始点为(1，1.5)T的运动轨迹图

(3)初始点(-2，0)T在可行域的边界上。从图4可以看到，当t>0.5s时状态向量x(t)在可行域内且趋向稳定，程序结束时的值为(-1.102 8，0.551 4)T，显然是原始优化问题的最优解。

Figure 4　Move track of the initial point (-2，0)T图4　初始点为(-2，0)T的运动轨迹图

实验3

Figure 5　Move tracks of three additional state vectors图5　附加状态向量运动轨迹图

6结束语

本文介绍了一类非李普西茨受限优化问题，通过光滑逼近技术以及结合惩罚函数方法，构建了光滑神经网络模型，扩大了G-NPC模型的应用范围，为解决信号重建、图像修复等应用提供了一种新的神经网络模型。本文对受限非李普西茨优化问题的稳定点进行了定义。在一个比较温和的条件下，证明了解的全局性、有界性，以及所建光滑神经网络的任意聚点是原始优化问题的稳定点等结论。最后，通过几个仿真实验验证了理论的确性。除此之外，通过详细的实验对比，证明本理论和文献[10]提出的理论一样，都能实现找到原始优化问题最优解的目的，只是本文不需进行投影计算而已。

[1]GaoYun.Theneuralnetworkforsovingoptimationproblems[D].Wuxi:JiangnanUniversity，2011．(inChinese)

[2]TankDW,HopfieldJJ.Simpleneuraloptimizationnetworks:Ana/dconverter,signaldecisioncircuit,andalinearprogrammingcircuit[J].IEEETransactionsonCircuitsSystem，1986，33(5):533-541．

[3]KennedyM,ChuaL.Neuralnetworksfornonlinearprogramming[J].IEEETransactionsonCircuitsSystem,1988，35(5):554-562.

[4]HuangYuan-can.Lagrange-typeneuralnetworksfornonlinearprogrammingproblemswithinequalityconstraints[C]∥Procofthe44thIEEEConferenceonDecisionandControl，andtheEuropeanControlConference,2005:4129-4133．

[5]HuangYuan-can.AnewtypeofLagrangenonlinearprogrammingneuralnetwork[J].ACTAElectronicaSinica，2002，30(1):27-29．(inChinese)

[6]LiGuo-cheng,SongShi-ji,WuCheng.Generalizedgradientprojectionneuralnetworksfornonsmoothoptimizationproblems[J].ScienceChinaInformationSciences,2010,53(5):990-1005．

[7]LiuQing-shan,WangJun.Aone-layerrecurrentneuralnetworkforconstrainednonsmoothoptimization[J].IEEETransactionsonSystems,Man,andCybernetics—PARTB:Cybernetics，2011，41(5):1323-1333．

[8]LiuQing-shan，TangChuang-ying，HuangTing-wen.Aone-layerrecurrentneuralnetworkforreal-timeportfoliooptimizationwithprobabilitycriterion[J].IEEETransactionsonCybernetics，2013，43(1):14-23．

[9]ChenXiao-jun.Smoothingmethodsfornonsmoothnonconvexminimization[J].MathematicalProgramming，2012，134(1):71-99．

[10]BianWei,ChenXiao-jun.Smoothingneuralnetworkforconstrainednon-Lipschitzoptimizationwithapplication[J].IEEETransactionsonNeuralNetworkandLearningSystems,2012,23(3):399-411．

[11]FortiM,NistriP,QuincampoixM.Generalizedneuralnetworkfornonsmoothnonlinearprogrammingproblems[J].IEEETransactionsonCircuitsandSystems—I，2004，41(5):1741-1754．

[12]HanZheng-zhi,CaiXiu-shan,HuangJun.Thetheoryforcontrolsystemsdescribedbydifferentialconclusions[M].Shanghai:ShanghaiJiaoTongUniversityPress，2013．(inChinese)

[13]FilippovAF.Differentialequationswithdiscontinuousright-handside[M]∥MathematicsandItsApplications(SovietSeries).Boston,MA:Kluwer,1988．

[14]BetounesD.Differentialequations:Theoryandapplications[M].NewYork:Springer-Verlag,2009．

[15]AubinJP,CellinaA.Differentialinclusion:Set-valuedmapsandviabilitytheory[M].NewYork:Springer-Verlag,1984．

[16]HamFM,KostanicI.Principlesofneurocomputingforscience&engineering[M].YeShi-wei，WangHai-juanTranslated.Beijing:ChinaMachinePress，2007．(inChinese)

[1]高云.求解优化问题的神经网络方法[D].无锡:江南大学，2011．

[4]黄远灿.一种新型的Lagrange非线性规划神经网络[J].电子学报，2002，30(1):27-29．

[12]韩正之，蔡秀珊，黄俊.微分包含控制系统理论[M].上海:上海交通大学出版社，2013．

[16]HamFM,KostanicI.神经计算原理[M].叶世伟,王海娟,译.北京:机械工业出版社,2007．

喻昕(1973-),男，重庆荣昌人，博士，教授，CCF会员(E200011072M)，研究方向为人工神经网络和优化计算。E-mail:Yuxin21@126.com

YUXin,bornin1973,PhD,professor,CCFmember(E200011072M)，hisresearchinterestsincludeartificialneuralnetworks,andoptimizationcalculation.

谢缅(1990-),女，湖北潜江人，硕士生，研究方向为人工神经网络和优化计算。E-mail:996927697@qq.com

XIEMian,bornin1990,MScandidate,herresearchinterestsincludeartificialneuralnetworks,andoptimizationcalculation.

李晨宇(1989-),男，湖南宁远人，硕士生，研究方向为人工神经网络和优化计算。E-mail:329243522@qq.com

LIChen-yu,bornin1989,MScandidate,hisresearchinterestsincludeartificialneuralnetworks,andoptimizationcalculation.

Solvingnon-Lipschitzoptimizationproblemsbysmoothingneuralnetworks

YUXin,XIEMian,LIChen-yu

(SchoolofComputer&ElectronicsandInformation，GuangxiUniversity,Nanning530004,China)

Abstract:In order to seek to optimal solution satisfying the necessary conditions of optimality, aiming at the optimization problems that objective functions are non-Lipschitz and the feasible region consists of linear inequality or nonlinear inequality, we design a new smooth neural network by the penalty function method and the smoothing approximate techniques which convert non-smoothing objective functions into smoothing functions. Detailed theoretical analysis proves the uniform boundedness and globality of the solutions to smooth neural networks, regardless of the initial points inside or outside of the feasible domain. Moreover, any accumulation point of the solutions of to smooth neural networks is a stationary point of the optimization promble. Numerical examples also demonstrate the effectiveness of the method.

Key words:non-Lipschitz function;smoothing approximate techniques;stationary point;accumulation point

作者简介:

doi:10.3969/j.issn.1007-130X.2015.12.011

中图分类号：TP183

文献标志码：A

基金项目：国家自然科学基金资助项目(61462006)；广西区自然科学基金资助项目(2014GXNSFAA118391)

收稿日期：修回日期：2015-03-23

文章编号：1007-130X(2015)12-2262-08