导数知识的联系与贯通

陆贤彬+丁江涛

导数作为工具，其功能十分强大，可以研究函数的单调性、可以研究函数的极值（或最值），还可以研究在某种条件下不等式（恒）成立的问题等.用导数处理这些问题，思路明确、方法简单、易于掌握，并且能凸显问题之间的相互联系、相互转化以及相互贯通的辩证关系.下面我们就以“简”的视角来理解一下作为工具的导数.

1.导数是用相对简单的雨数研究复杂的雨数

我们看下面几个导数：

若f（x）=c（c是常数），则f'（x）=0；

若f（x）=ax+b，（a，b是常数且a≠O），则f'（x）=a；

若f（x）=ax?+bx+c，（a，b，c是常数且a≠0），则f'（x）=2ax+b；

若f（x）=ax?+bx?+cx+d，（a，b，c，d是常数且a≠0），则f'（x）=3ax?+2bx+c；

可见，导数可以将研究“常数”转化成研究“0”；研究“一次函数”转化成研究“常数”；研究“二次函数”转化成研究“一次函数”；研究“三次函数”转化成研究“二次函数”等等……也就是说通过研究低一次的函数来研究高一次的函数，这自然简单了.

我们再看下面几个导数：

若f（x）=1nx，则f'（x）=1/x；

若f（x）=x+1nx，则f'（x）=1+1/x；

若f（x）=logax，（a是常数且a>0，a≠1）则f'（x）=；

可见，导数可以将研究“对数”转化成研究“分式”，当然要简单些，我们还可以再列举一些，同学们可以自己试试.

2.导数是用相对简单的方法替代复杂的方法

我们看一个例子：求函数f（x）=（x-2）?（x-1）的单调增区间.

方法一：不用导数处理，从函数单调性的定义人手.

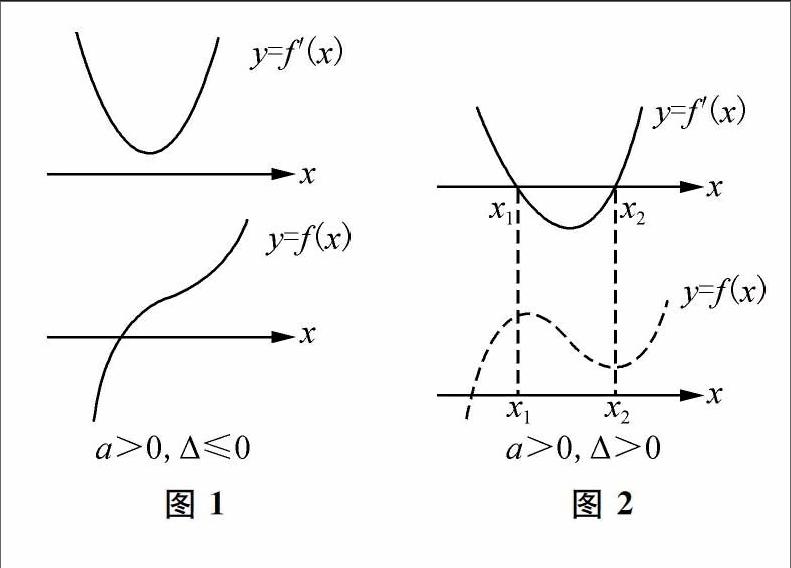
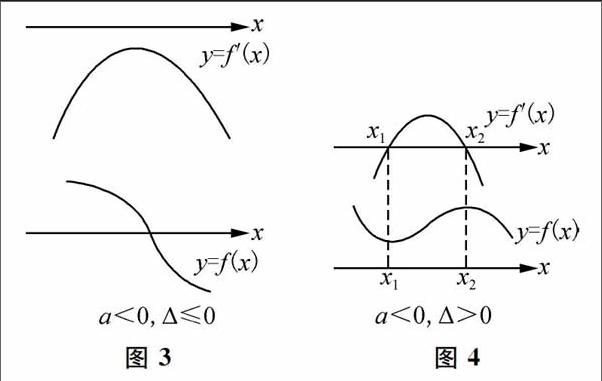
设xl

因此可以分别在区间（-∞，4/3），（4/3，2），（2，+∞）上研究函数的单调性.

不再做下去了，下面还有点复杂，同学们自己可以做一下.这里不是介绍方法而是想说明一下：用这一方法处理起来比较复杂.

方法二：用导数处理.

f'（x）=2（-2）（x-1）+（x-2）?=（x-2）（3x-4）.由f'（x）>O得函数f（x）一（x-2）?（x-1）单调增区间为（-∞，4/3），（2，+∞）.

比较一下，明显地看出：方法2简单.

事实上，对于方法1，要比较任意两个白变量对应的函数值的大小，而且白变量所在的区间还需要先确定，这本身也很难，对于方法2，只要先求出基本函数的导数，再解一个关于x的二次不等式就行了.

3.导数求得单调性进而解决一系列问题

运用导数的方法研究函数的性质，其核心是研究函数的单调性.这是因为如果知道函数的单调性，我们就可以画出它的草图，结合.可观察函数的“极值”，进而可求“最值”、“值域”，也可处理“函数的零点”、“不等式恒成立”等问题，判断函数的单调性是运用导数的方法研究函数性质的基石.问题是如何才能做到既直观、义准确呢？

首先“以数定形”，根据导数的定义，我们可以用“关于导函数的不等式”来刻画“函数的单调性”：若，则函数是增函数；则y=f（x），x∈A是减函数.所以，研究函数单调性的关键是判断导函数y=f'（x），x∈A的函数值的符号，即判断“f'（x）>o”或“、f'（x）<0”.对于这个问题，大多数同学会先求解方程f'（x）=0的根，然后再判断何时为“正”、何时为“负”，这样处理也未尝不可，但由于没有抓住问题的关键——解不等式，有时容易犯错，我们可以尝试“以形助数”.

以三次多项式函数为例，设y=f（x）的导函数f'（x） =ax?+bx+c（a≠0），试讨论其单调性.

分析：对其中的a和△进行讨论，共分四种情况，我们分别作出其导函数和函数的草图：见（图1～图4）.

结合这些.，所有三次多项式函数的单调性一目了然.这里强调的是：当△>o时，宜将f'（x）因式分解，写成两根式：f'（x）=a（x-x1）（x-x2），这样处理不仅可以快捷地作图，而且能直观地判断导函数的符号.

仍以上面的题目为例，可以列一个表，解决一系列问题.

求函数f（x）=（x-2）?（x-1）的单调增区间、单调减区间、极大值、极小值.

解 f'（x）=2（-2）（x-1）+（x-2）?= （x-2） （3x-4）.

列表：

故求函数f（x）=（x-2）?（x-1）的单调增区间为（-∞，4/3），（2，+∞），递减区间是（4/3，2），极大值是4/27，极小值是o.当然本题还可以在某个范围内求最值（如：x∈[0，2]时，求f（x）的值域）；或是在某种条件下不等式恒成立的问题（如：当x∈[0，2]时，不等式（-2）?（x-1）≤a恒成立，求a的范围）等等.

用导数可以解决一系列有联系的问题，函数中的很多问题从而得到有效贯通，这为我们整体认识函数提供了一个很好的平台.随着学习的深入，我们会逐步感悟导数的功力，逐步感悟知识间的联系与贯通，逐步感悟数学的本质是求简.