系统辨识在伺服系统动态特性测试中的应用

朱燕梅，侯　文，郑浩鑫，张　寅

(中北大学 a. 仪器与电子学院；　b. 信息与通信工程学院；　c. 机械与动力工程学院，　太原 030051)



系统辨识在伺服系统动态特性测试中的应用

朱燕梅a，侯文b，郑浩鑫c，张寅a

(中北大学 a. 仪器与电子学院；b. 信息与通信工程学院；c. 机械与动力工程学院，太原 030051)

摘要：将系统辨识引入伺服系统的测试中，采用多新息随机梯算法辨识出系统的传递函数。通过由辨识得到的传递函数来计算系统的阶跃响应特性和频率特性，既减少了测试项目，又提高了效率。基于舵机系统的测试需求完成了测试实验，与传统测试方法相比幅频特性误差小于0.39 dB，相频特性误差小于4.9°，上升时间的误差控制在6.29%以下，实验结果表明，通过系统辨识来计算伺服系统性能指标取得了良好的测试效果。

关键词：伺服系统；系统辨识；多新息随机梯度算法；动态特性

0引言

伺服系统又称随动系统[1]，为提高伺服系统的控制精度和控制效率，需要对系统进行性能测试，分析测试结果，然后依据分析结果对系统进行调试，保证系统能够在最好的状态下运行。因此，伺服系统的性能测试对系统的研究、分析以及改进具有十分重要的实用价值[2]。

将系统辨识应用到伺服系统的测试中，辨识出系统的传递函数，用辨识得到的传递函数计算被测系统的各项特性。一方面可以制定相应的测试指标或对现有的指标进行检验；另一方面，系统的模型和传递函数确定之后，将计算出的各项特性直接作为测试结果，可以减少测试项目，进而大幅缩短测试时间。由此可见，系统辨识在伺服系统性能测试中的应用具有重要的意义[3]。

1系统辨识及辨识算法

系统辨识，就是在输入数据和输出数据的基础上，从所选择的一类模型集中，来确定一个能够充分表征被测系统的模型，准则函数采用不同的优化方法时，可以得到不同的辨识方法。辨识方法有最小二乘法、梯度辨识法、迭代辨识法、辅助模型辨识法、多新息辨识法和耦合辨识法等[4-5]。本文采用多新息随机梯度辨识方法，A(z)、B(z)、D(z)是z-1的系数为常数的时不变多项式

A(z)=1+a1z-1+a2z-2+…+anaz-na，ai∈R

(1)

B(z)=b1z-1+b2z-2+…+bnbz-nb，bi∈R

(2)

D(z)=1+d1z-1+d2z-2+…+dndz-nd，di∈R

(3)

定义参数向量θ和信息向量φ(t)

θ=[a1,a2,…,ana,b1,b2,…,bnb]T

(4)

φ(t)=[-y(t-1),-y(t-2),…,-y(t-na)，

u(t-1),u(t-2),…,u(t-nb)]T

(5)

则受控自回归滑动平均模型可以写为

y(t)=φT(t)θ+D(z)v(t)

(6)

梯度辨识算法是沿着所采用的准则函数的负梯度方向对参数的估计进行搜索，参数最优值的获取通过在误差准则函数的负梯度方向上减少参数估计值与真值的差距来实现[6]。多新息随机梯度算法，将标量新息e(t)∈R扩展为新息向量 E(p,t)∈Rp，p≥1为新息长度，即多新息[7]。新息e(t)使用的是参数估计刷新前的数据θ(t-1)计算的，其表达式为

e(t)=y(t)-φT(t)θ(t-1)

(7)

(8)

其中

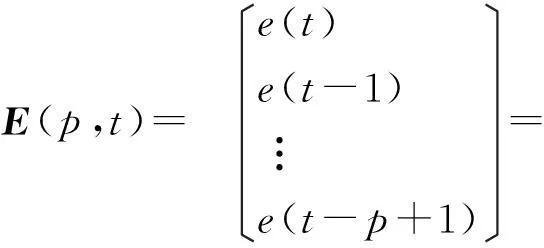
(9)

定义准则函数

(10)

式中：Φ(p,t)为信息矩阵；Y(p,t)为堆积输出向量

Φ(p,t)=[φ(t),φ(t-1),…,φ(t-p+1)]

(11)

Y(p,t)=[y(t),y(t-1),…,y(t-p+1)]T

(12)

多新息随机梯度算法如下

(13)

(14)

r(t)=r(t-1)+‖Φ(p,t)‖2，r(0)=1

(15)

当新息长度p=1时，多新息随机梯度算法就简化为随机梯度算法[8]。多新息随机梯度算法在每步递推计算参数估计时，不仅使用了当前数据和新息，而且使用了过去的数据和新息，因此，该算法收敛速度快；在相邻两时刻递推计算参数估计时，重复利用时刻较前的数据和新息，因此，参数估计精度较高，而且在相同数据长度下，增加p能减小参数估计误差，而且增加的计算量是计算机完全能够胜任的[9]。

2用辨识结果计算伺服系统性能指标

伺服系统的特性可以分为静态特性和动态特性，静态特性反应了系统的非线性程度，动态特性包括阶跃响应特性、频率特性等[10]。将系统辨识应用到测试中，就是通过辨识得到系统的传递函数，然后，用传递函数来计算伺服系统的动态特性。

在计算系统的频率特性时，可以通过相应的公式将系统的传递函数转换为频率响应函数，从而直接算得幅频特性与相频特性，在减少计算量的同时不会因为阶次的增加而使计算变得过于复杂。

若通过辨识得到系统的无噪声差分方程模型为

y(t)+a1y(t-1)+a2y(t-2)+…+anay(t-na)=

b1u(t-1)+b2u(t-2)+…+bnbu(t-nb)

(16)

式中：ai∈R ，bi∈R，i=1,2,…,∞，则可通过z变换得到它的离散传递函数

(17)

令z=ejω，可以得到系统的频率响应函数G(ejω)，其中，ω为角频率，ω=2πf/fs，f为实际频率，即输入量，fs为采样频率[11]。通过欧拉公式

ejx=cosx+jsinx

(18)

将频率响应函数转换为Au(f)+jB(f)的形式，进一步可得到幅频特性与相频特性的公式为

(19)

(20)

代入不同的频率f，即可得到被测系统的幅频特性以及相频特性。

在计算阶跃特性时，将阶跃信号作为输入带到这个差分方程中，得到相应的输出，通过输入和输出来计算系统的阶跃响应特性。

3实验设计

为验证前述系统辨识在伺服系统性能测试中的应用，以导弹舵机系统为测试对象进行实验研究。

对于实际的导弹舵机系统，其传递函数是未知的，即使存在系统的仿真模型，由于各种因素的影响(如构成系统的零部件的微小差异、间隙、摩擦等)实际系统与理论模型之间往往有所差异。那么，如何选择检验辨识结果的标准也就成为实验要解决的重要问题，动态特性是系统重要的特性，直接测得的动态特性的测试精度较高，因此，可以作为检验辨识结果的标准。检验辨识效果的方法原理图如图1所示，在辨识完成后将辨识得到的传递函数变换为频率响应函数，计算幅频特性和相频特性，与直接测得的数据结果进行比较，逐点求得误差，取最大误差作为验证辨识效果的标准。

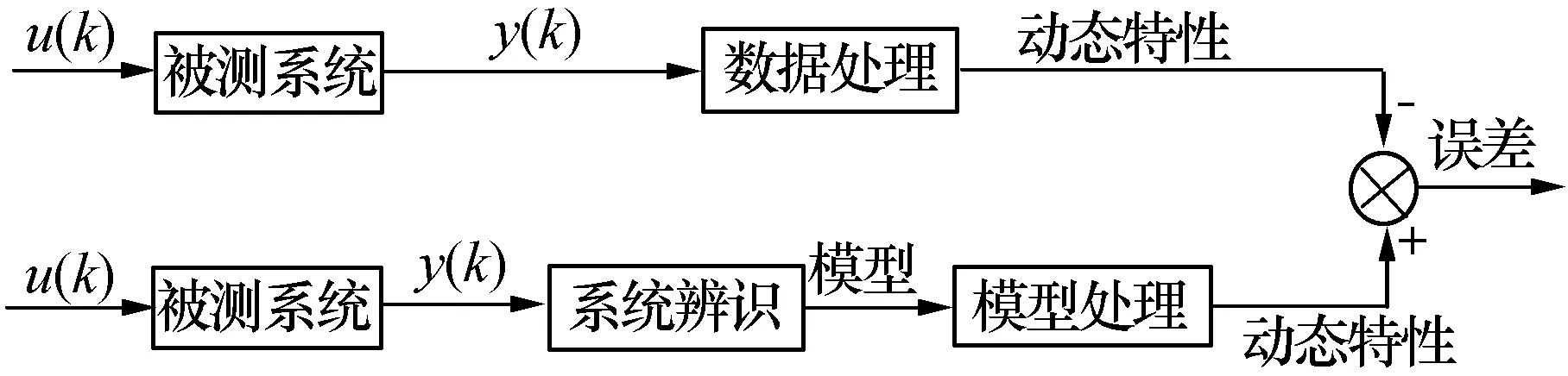
图1　检验辨识效果的方法

采用多新息随机梯度算法，新息长度P=8对舵机伺服系统进行参数辨识，辨识得到的系统的各个参数值如表1所示。

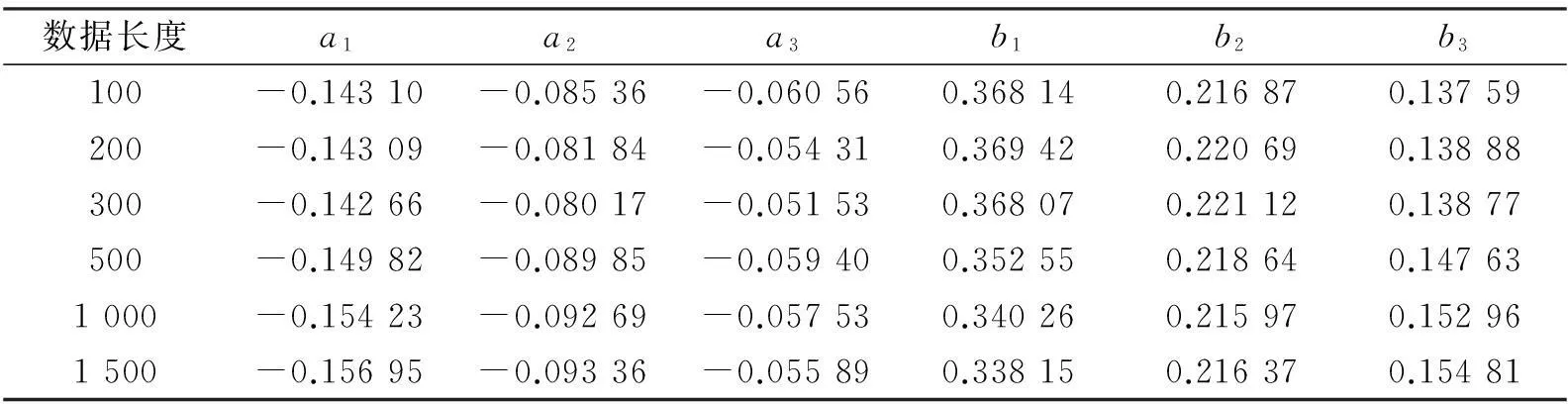
表1　辨识模型参数的估计

在辨识完成后将辨识得到的传递函数变换为频率响应函数，计算幅频特性和相频特性，与由舵机输入输出数据直接测得的数据结果进行比较，逐点求得误差，取最大误差作为验证辨识效果的标准。输入信号幅值为5°的白噪声，数据长度定为20 s。采用受控自回归滑动平均模型进行辨识，通过辨识模型算得的频率特性如图2所示。

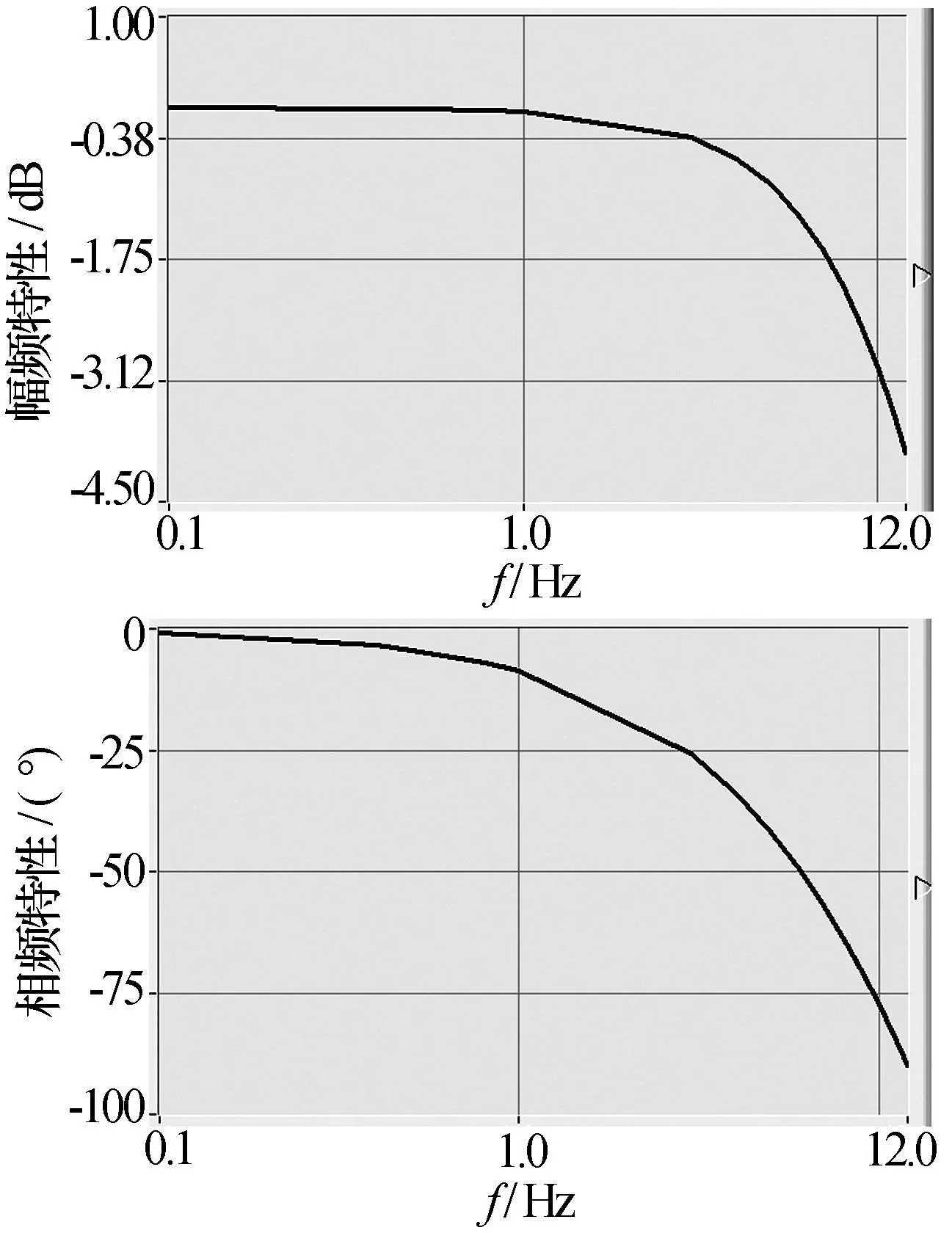
图2　通过辨识模型算得的频率特性曲线

由表2中频率特性测试数据分析可得，幅频特性误差小于0.39 dB，相频特性误差小于4.9°。通过辨识模型算得的阶跃响应特性曲线图如图3所示，将上升时间设定为系统的输出值从稳态值(通过计算稳定部分的均值得到)的5%到95%所需的时间。

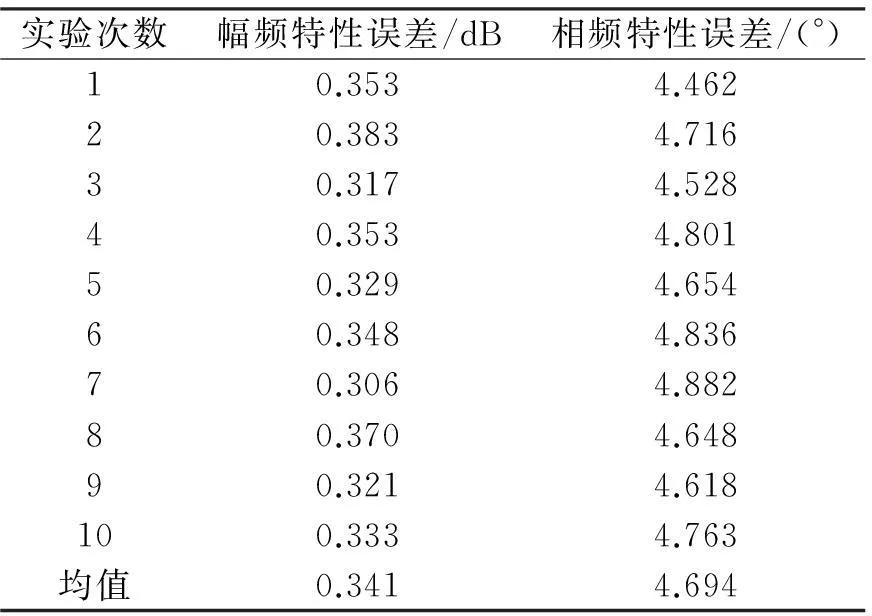
表2　辨识模型的频率特性误差

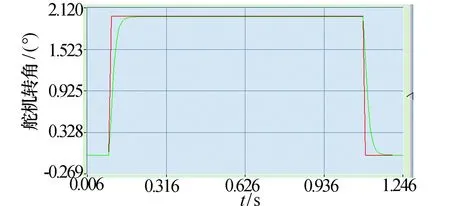
图3　通过辨识模型算得的阶跃响应特性曲线图

由于已经去除了模型中噪声的部分，因此，从图中可以更直观地看出系统没有超调。计算得上升时间均值为35.5 ms。而直接由输入输出曲线测得的正向和反向的上升时间为33.4 ms，输出信号没有超调或超调很小且已淹没在噪声中，因此，也无法准确测得系统超调量和衰减度。通过辨识出系统的传递函数后，再对系统进行测试，其数据曲线相比于直接测试结果更加直观地反应了系统的阶跃响应特性。

4结束语

将系统辨识的理论和内容引入到伺服系统的测试中，辨识出系统的模型和传递函数，并通过实验对某舵机系统进行了测试，得到了动态特性的测试结果，通过对比动态特性测试结果和辨识模型计算动态特性的测试结果，验证了辨识结果的准确性，而且丰富了伺服系统的测试方法。

参 考 文 献

[1]王刚. 直流电机伺服控制技术研究与实现[D]. 大连: 大连理工大学, 2013.

WANG Gang. Research and implementation of the DC motor servo control technology[D]. Dalian: Dalion University of Technology, 2013.

[2]张寅，侯文，李建民，等. 基于Multitone信号的伺服系统频率特性测试方法研究[J]. 计算机测量与控制, 2014, 22(10): 3129-3131.

ZHANG Yin, HOU Wen, LI Jianming, et al. Research on frequency response testing method for servo system based on multitone signal[J]. Computer Measurement & Control, 2014, 22(10): 3129-3131.

[3]钟玉涛. 伺服控制测试分析系统的设计[D]. 武汉：华中科技大学, 2007.

ZHONG Yutao. A design of test and analysis of servo control[D]. Wuhan: Huazhong University of Sicence & Technology, 2007.

[4]ZADEH L A. From circuit theory to system theory[J]. Proceedings of the IRE, 1962, 50(5): 856-865.

[5]丁锋. 系统辨识(4)：辅助模型辨识思想与方法[J]. 南京信息工程大学学报(自然科学版), 2011, 3(4): 289-318.

DING Feng. System idenfification. Part D: Auxiliary model identification idea and methods[J]. Journal of Nanjing University of Information Science and Technology (Natural Science Edition), 2011, 3(4): 289-318.

[6]丁锋，杨家本． 随机梯度算法的收敛性分析[J]． 清华大学学报 (自然科学版)，1999，39(1) : 83-86.

DING Feng, YANG Jiaben. Covergence analysis of stochastic gradient algorithms[J]. Journal of Tsinghua University (Science and Technology), 1999, 39(1): 83-86.

[7]DING F, CHEN T. Performance analysis of multi-innovation gradient type identification methods[J]. Automatica, 2007, 43(1): 1-14.

[8]丁锋. 系统辨识(6)：多新息辨识理论与方法[J]. 南京信息工程大学学报 (自然科学版), 2012, 4(1): 1-28.

DING Feng. System identification. Part F: multi-innovation identification theory and methods[J]. Journal of Nanjing University of Information Science and Technology (Natural Science Edition), 2012, 4(1): 1-28.

[9]WANG W, DING F, DAI J Y. Maximum likelihood least squares identification for systems with autoregressive moving average noise[J]. Applied Mathematical Modelling, 2012, 36(5):1842-1853.

[10]曹宇. 伺服系统特性测试平台设计[D]. 武汉：华中科技大学, 2013.

CAO Yu. Design of the characteristics testing platform on servo system[D]. Wuhan: Huazhong University of Science & Technology, 2013.

[11]范金锁, 张志成, 张合新. 基于虚拟仪器的导弹控制系统测试研究[J]. 仪器仪表学报, 2007,28(4): 260-266.

FAN Jinsuo, ZHANG Zhicheng, ZHANG Hexin. Resaerch of missile control system testing based on virtual instrument[J]. Chinese Journal of Scientific Instrument, 2007, 28(4): 260-266.

朱燕梅女，1986年，硕士研究生。研究方向为自动化测试与控制技术。

费翔宇男，1982年生，工程师。研究方向为生命搜救雷达、穿墙侦察雷达等专用探地雷达信号处理。

冯温雅女，1983年生，工程师。研究方向为探地雷达信号处理。

王成浩男，1989年生，工程师。研究方向为探地雷达信号处理。

System Identify Applied in Dynamic Characteristics

Testing for Servo Control System

ZHU Yanmeia，HOU Wenb，ZHENG Haoxinc，ZHANG Yina

(a. School of Instrument and Electronics;b. School of Information and Communication Engineering;

c. School of Mechanical and Power Engineering, North University of China,Taiyuan 030051, China)

Abstract：System identification is introduced into servo system testing and MISG is used to calculate the transfer function of the system. Step response characteristic and frequency response of the system are calculated through the transfer function which are obtained by system identification, which not only decreases testing items but also improves testing efficiency. A test experiment was completed on the test requirement for an actuator. Compared with the traditional testing method, the experimental results show that the error of amplitude-frequency characteristic kept within 0.39 dB and the error of phase-frequency characteristic kept within 4.9° and the rising time was kept within 6.29% . Test effect is given exellent results througn performance indexes of servo system obtained by system identification.

Key words：servo system; system identify; MISG; dynamic characteristics

DOI：·天馈伺系统· 10.16592/ j.cnki.1004-7859.2015.12.013

收稿日期：2015-07-22

修订日期：2015-09-23

通信作者：朱燕梅Email：757086161@qq.com

基金项目：总装国防科技基金资助项目

中图分类号：TP206

文献标志码：A

文章编号：1004-7859(2015)12-0057-04