短波FH/OFDM通信系统抗跟踪式干扰性能分析*

甘海慧,熊俊俏,曹新莉,陈爱杰

(1.武汉烽火网络有限责任公司，武汉 430074；2.武汉工程大学 电气信息学院，武汉 430205)

短波FH/OFDM通信系统抗跟踪式干扰性能分析*

甘海慧1,**,熊俊俏2,曹新莉2,陈爱杰2

(1.武汉烽火网络有限责任公司，武汉 430074；2.武汉工程大学 电气信息学院，武汉 430205)

摘要：对于短波多载波跳频通信系统，跟踪式干扰是一种有效的干扰模式。分析了正交频分复用(OFDM)部分子信道干扰与符号误码率的关系，通过仿真获得了最佳跟踪干扰的部分时间参数，结合OFDM频谱结构与干扰频谱关系，推导了高斯信道条件下部分频带干扰和多音干扰时系统误码率，分析了短波FH/OFDM通信系统抗跟踪式干扰的误码率性能，仿真结果表明：跟踪干扰时间窗口对误码率的影响与部分频带干扰因子和信干比有关；在部分频带干扰与部分时间干扰之间，存在等效的干扰效果区域；多音干扰因子越大，系统所受影响越大，跟踪干扰时间窗口对误码率的影响与多音干扰因子和信干比有关，针对OFDM符号的多音干扰影响要远大于部分频带干扰的影响；跳频与OFDM技术的结合、提高载波跳速、减小跟踪式干扰对OFDM符号的影响，也是消除多音干扰的重要手段。

关键词：短波跳频；多载波调制；跟踪式干扰；部分频带干扰；多音干扰；抗干扰性能分析

doi:10.3969/j.issn.1001-893x.2015.02.008

引用格式：甘海慧,熊俊俏,曹新莉,等.短波FH/OFDM通信系统抗跟踪式干扰性能分析[J].电讯技术，2015,55(2):156-162.(in English)[GAN Haihui,XIONG Junqiao,CAO Xinli,et al.Tracking Interference Suppression Performance Analysis of Shortwave FH/OFDM Communication System[J].Telecommunication Engineering,2015,55(2):156-162.]

中图分类号：TN911.2

文献标志码：码：A

文章编号：号：1001-893X(2015)02-0156-07

收稿日期：*2014-08-15；修回日期：2014-12-26Received date:2014-08-15；Revised date：2014-12-26

基金项目：湖北省自然科学基金资助项目(2014CKC524)；武汉工程大学科研基金资助项目(K201421)

Abstract：Tracking interference is an effective interference patterns for a shortwave multi-carrier frequency-hopping(FH) communication system.In this paper,the relationship between sub-channels interference and orthogonal frequency division multiplexing(OFDM) symbol error rate is analyzed,and the part time parameters of best tracking interference are obtained by simulation,the system bit error rate(BER) in partial band jamming and the multi-tone interference is derived under Gaussian channel according to the relationship between OFDM spectrum and interference spectral,and the BER performance of anti-tracking interference is analyzed.Simulations show that:the BER is related not only with the tracking interference time window,but also with the partial-band interference factor and signal to interference ratio;there is interference equivalent region between the partial-band interference and the part-time interference;when the factor of multi-tone jamming is greater,the effect of the time-window on system is greater,the BER is related not only with the tracking interference time window,but also with the multi-tone interference factor and signal to interference ratio,and the effect of multi-tone interference on OFDM symbol is more critical than that of partial band interference;by combining FH and OFDM,increasing the carrier FH rate and reducing the impact of tracking interference on OFDM symbols,multi-tone interference can be eliminated effectively.

作者简介：

Foundation Item:The Natural Science Foundation of Hubei Province(2014CKC524);The Scientific Research Foundation of Wuhan Institute of Technology(K201421)

Tracking Interference Suppression Performance Analysis of

Shortwave FH/OFDM Communication System

GAN Haihui1,XIONG Junqiao2,CAO Xinli2,CHEN Aijie2

(1.Wuhan FiberHome Networks Co.,Ltd.,Wuhan 430074,China；

2.College of Electrical and Electronic Engineering,Wuhan Institute of Technology,Wuhan 430073,China)

Key words：shortwave frequency hopping;multi-carrier modulation;tracking interference;partial band interference;multi-tone interference;interference suppression performance analysis

1引言

短波多载波跳频(Frequency Hopping，FH)通信技术兼具较强的抗干扰、抗多径衰落的能力，从而在战术通信方面等得到了广泛应用，但易受到各种人为干扰，如针对宽带通信的宽带干扰、部分频带干扰，以及针对正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统的单音和多音干扰等[1]。目前，FH/OFDM系统抗干扰的性能分析通常考虑两种情形：一是干扰方了解跳频频率序列，对所有跳频频点实施干扰，但不了解OFDM具体参数对OFDM信号进行各种形式的干扰[2-3]；二是干扰方不了解跳频频率序列，对部分跳频频点实施干扰，此时假设一旦某跳频频点受到干扰，则该频点所携带的OFDM符号全带宽受干扰[4]。针对OFDM信号的多音干扰，文献[5-6]进行了分析。但实际上由于干扰方并不了解跳频频率序列变化规律以及监听、处理时间的延迟，无法对跳频频率驻留时间段全部干扰，对每一跳驻留时间存在部分干扰，即对OFDM符号形成部分时间干扰，结合干扰方的具体干扰模式，存在部分时间的子信道干扰、部分时间的部分频带干扰以及部分时间的多音干扰等。

本文首先分析OFDM子信道误码率与符号误码率的关系，并推导了最佳跟踪式干扰的参数，接下来从频谱受干扰角度出发，分别分析宽带噪声干扰、多音干扰对OFDM系统的影响，最后结合部分时间干扰开展跟踪式干扰的研究，分析跟踪式干扰条件下FH/OFDM系统的抗部分频带干扰和抗多音干扰的能力。

2最佳跟踪式干扰参数分析

OFDM的子载波数为M，每个子载波上传输QPSK调制信号，若第i个子信道上的信噪比为γb(i)，对应M路子载波，OFDM符号的平均比特误码率为[7-8]

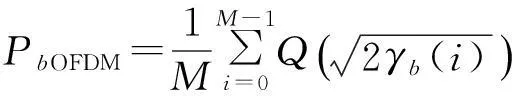
(1)

若OFDM的M个子信道中，有m个子信道被干扰，则有M-m个子信道没有被干扰，被干扰比为ρ=m/M，令γb0为子载波被干扰时的信噪比，γb1为子载波未被干扰时的信噪比，对应的OFDM符号的平均比特误码率为[9]

(2)

式中，Eb为码元的能量，Nj为干扰的总能量。

式(2)为OFDM符号的部分子载波受到干扰，且干扰时间为OFDM符号全周期。若假设干扰方了解跳频工作频率集或跳频工作频段，但对跳频频率序列变化无法预测，则可以采用跟踪式干扰，即干扰方施加的干扰仅仅为OFDM符号周期的部分时段干扰。设干扰时长为LTs(Ts为调制信号周期)，OFDM周期为MTs，则干扰时长比为ρT=L/M。

在OFDM发送端，发送数据为{Xk,k=0,1,2,…,M-1}，而接收端信号为

y(m)=αx(m)+nj(m)WL(m)+n(m),

m=0,1,2,…,M-1。

(3)

式中，α为频率非选择性慢衰落信道的衰落因子，n(m)为高斯白噪声干扰，nj(m)为干扰信号，WL(m)为干扰窗函数，

(4)

接收端基带信号经过FFT变换，得到

αX(k)+FFT{nj(m)WL(m)}+n(k),

k=0,1,2,…,M-1。

(5)

式中，高斯白噪声n(k)对每个子载波信号解调时形成干扰，人为施加的干扰信号nj(m)经过FFT变换，将对特定子信道或全部子信道形成干扰，这取决于干扰的具体形态，包括干扰时长、窗函数的选择等。

根据式(5)，干扰与加窗函数的频谱分布对每个子载波均可能形成干扰。在干扰能量一定时，干扰时长越短，则干扰带宽越宽，对每个子载波的干扰功率下降；反之，干扰时长越长，则干扰带宽越窄，形成对部分子载波的强烈干扰。以宽带干扰为例，对高斯白噪声频谱干扰进行时域加窗，将改变高斯白噪声的频谱结构，其噪声频谱为非均匀分布，因此，式(2)是将干扰信号简化处理的结果。

对于跟踪式干扰，在信干比较小时，即小于1 dB，由于干扰信号功率较大，此时干扰所占时间比只要在0.1～0.2即可对系统造成较好的干扰效果，而当信干比大于2 dB后，要取得较好的干扰效果，干扰所占时间比ρT应大于0.5～0.6，当信干比大于5 dB时，不适合采用该干扰方式。通常，对通信实施干扰，施加方应具有足够的干扰功率，考虑ρT=0.5实施跟踪干扰。

3宽带噪声干扰对OFDM信号的影响

噪声干扰的影响体现在频谱结构上，由于FH/OFDM信号频谱为多载波宽带频谱，与传统的跳频信号的单载波不同，宽带干扰信号对OFDM信号频谱的干扰存在不同的模型。

假设OFDM符号为矩形脉冲，其功率谱密度(Power Spectral Density，PSD)为[10]

(6)

式中，M为子载波数目，Psub为OFDM符号的子载波功率，Wsub为子载波的频率间隔。

假设频带干扰的PSD为

(7)

式中，PJ和WJ为干扰信号的功率和带宽，干扰信号与OFDM信号的中心频率距离为fd。

当OFDM符号的部分子载波被干扰时，平均差错率为

(8)

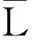
3.1　高斯信道条件下阻塞干扰的影响

在高斯信道条件下，OFDM系统的误码率性能取决于有效信噪比γk，考虑到OFDM信号的快速傅里叶变换(Fast Fourier Transform，FFT)，利用Cauchy-Schwarz不等式，信噪比γk为

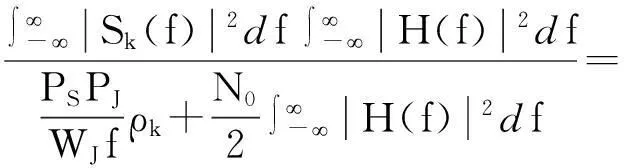
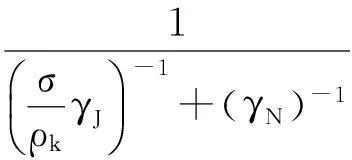
(9)

系统采用BPSK调制时，平均误码率为

(10)

当受干扰的子载波数L等于OFDM子载波总数M时，为阻塞干扰，属于宽带噪声干扰，干扰功率在整个频带上，简化考虑，其干扰效果与白噪声干扰(AWGN)的一样，干扰噪声的功率谱密度为

PSDJ=N0+NJ。

(11)

式中，N0为复AWGN的噪声功率谱密度，NJ为阻塞干扰的功率谱密度。

若全时段干扰，则在AWGN信道环境下，BPSK的比特误码率为[12]

(12)

式中，Eb为OFDM信号的平均比特能量。

若不考虑信道的时变特性，在高斯白噪声信道条件下，OFDM符号的平均误码率与式(12)相同。FH/OFDM系统在高斯白噪声信道条件下，存在阻塞干扰时，系统误码率与信噪比的关系曲线如图1所示。

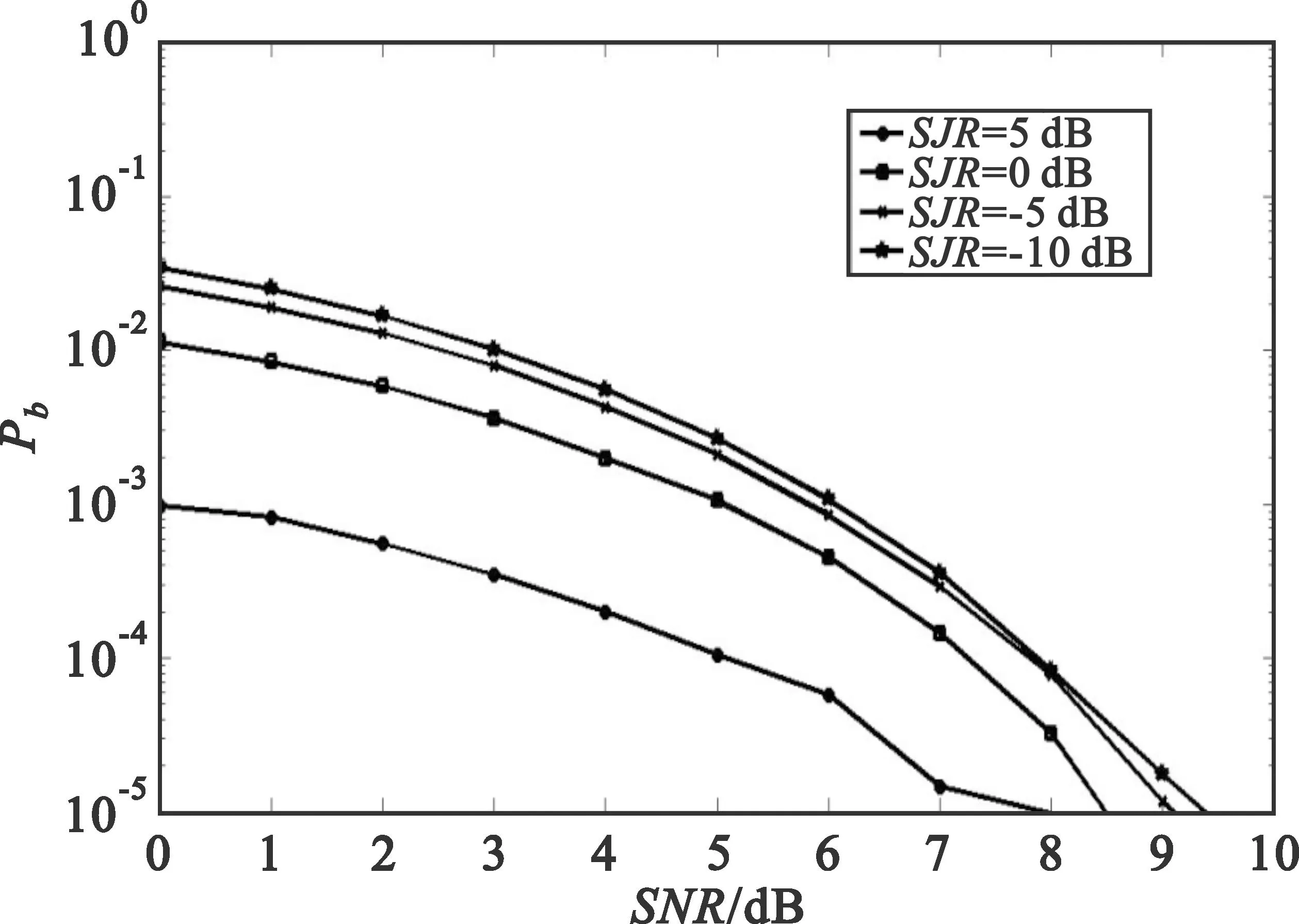
图1　阻塞干扰对FH/OFDM系统的影响

图1所示为阻塞干扰信干比分别为10 dB、5 dB、0 dB、-5 dB时，FH/OFDM系统的误码率性能。系统OFDM子载波为1024路，当干扰功率信干比大于0 dB时，干扰对误码率产生较大影响，而干扰功率信干比小于0 dB时，白噪声的影响比阻塞干扰的影响要强。

3.2　高斯信道条件下部分频带干扰的影响

对于式(8)，当干扰的子载波数目L不等于OFDM全部子载波数目M时，称为部分频带干扰，可等效为加性高斯白噪声，但是将其干扰功率集中在部分频带上。这里考虑干扰信号全部落在OFDM频带内，OFDM信号的部分子频带被干扰。令频带干扰因子ρf为

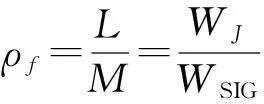
(13)

式中，WJ为干扰噪声的带宽，WSIG为OFDM信号的带宽。

在高斯白噪声信道条件下，部分被干扰的子载波其干扰噪声的功率谱密度为WJ/ρf，没有被干扰的子载波的噪声干扰为N0，式(10)的比特误码率可简化为[8]

(14)

考虑到部分频带干扰的功率谱密度NJ/ρf远大于信道的白噪声N0，误差函数等效为

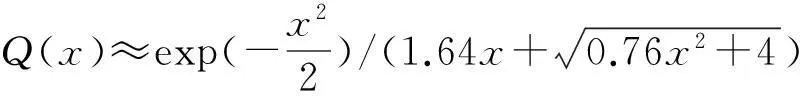
(15)

则式(14)可改写为

(16)

式中，信干比SIR=Eb/NJ。

图2为高斯白噪声信道条件下，部分频带干扰信干比为10 dB，不同频带干扰因子ρf时，FH/OFDM系统的误码率性能。系统OFDM子载波为1024路，当部分干扰频带因子ρf小于0.5时，其干扰效果与ρf等于0.1相当，即对误码率的影响很小；而当部分频带干扰干扰因子ρf大于0.5后，其影响越来越大；当ρf为1时，即全频带干扰，误码率恶化到10-3水平(信噪比为20 dB时)。 显然，在高斯白噪声信道条件下，部分频带的干扰因子越大，其对误码率的影响也越大。

图2　高斯信道条件下部分频带干扰的误码率

4多音干扰对OFDM信号的影响

多音干扰是将干扰能量集中干扰OFDM信号的部分子载波，干扰信号J(t)为一系列正弦波，其幅度为AJ，相位φJ为随机变量，在[0,2π]上均匀分布，干扰频率为fJ，其值大小也是OFDM子载波之一。

假设OFDM信号子载波的总数M中，被干扰的子载波数为L，则被干扰的比例为ρM=L/M。

以调制信号为BPSK为例，干扰信号J(t)虽然与子载波同频，但相位不一致，接收的解调信号为

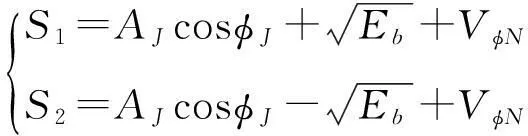
(17)

式中，φJ在[0,2π]上均匀分布，VφN代表白噪声干扰。

对二进制调制信号BPSK的解调中，对S1、S2的差错概率是相等的，在多音干扰下的BPSK的比特误码率为

PBPSK_MTJ=Pes1=Pr(S1<0)。

(18)

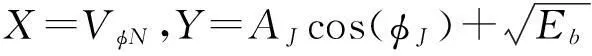
PBPSK_MTJ=Pes1=Pr(S1<0)=Pr(W<0)。

(19)

随机过程cos(θ)的概率密度函数为

(20)

则Y的概率密度函数(PDF)为

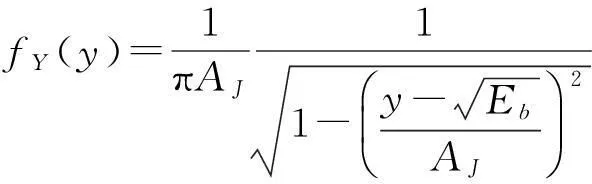
(21)

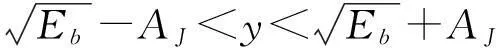
则

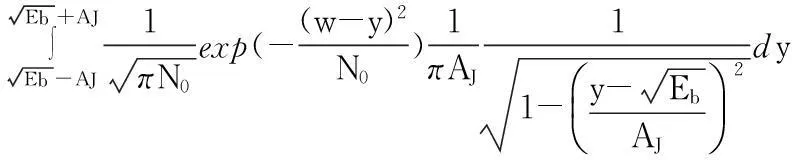
(22)

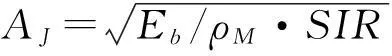
则有

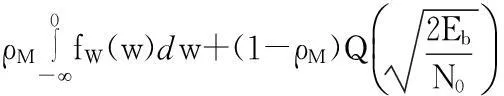
(23)

若忽略AWGN白噪声的影响，有

PBPSK(Eb，ρM，SIR)=Pes1=

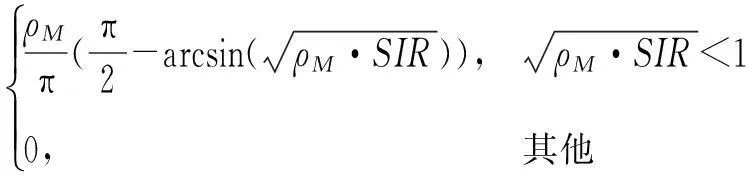
(24)

高斯白噪声信道条件下，存在多音干扰时误码率与信噪比的关系曲线如图3所示。当无噪声影响或信噪比较大时，误码率仅由多音干扰因子决定，近乎为常数；而信噪比较低时，白噪声的影响占主导作用，误码率随信噪比增大而下降，但当信噪比增大到一定限度时，误码率不再下降，反而由多音干扰因子决定。

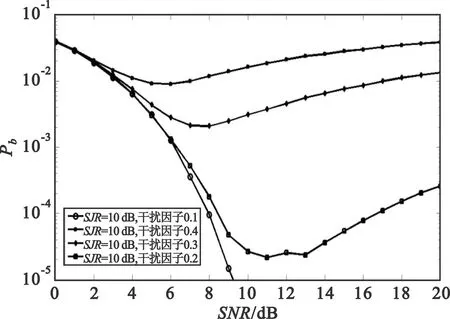
图3　高斯信道条件下，多音干扰的误码率关系

5跟踪式干扰仿真结果与分析

5.1　噪声与干扰的关系仿真

考察FH/OFDM系统，OFDM的子载波数为1024，考虑部分频带干扰因子ρf=0.3，信噪比分别取8 dB、7 dB、6 dB和5 dB。其中，部分频带干扰由噪声序列产生，其强度由信干比控制，经过快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)，获得干扰时域波形，再与噪声一并送入信道。经过蒙特卡洛法仿真，得到的误码率曲线如图4所示。

图4　FH/OFDM系统噪声、部分频带干扰误码率

根据仿真结果，白噪声为系统的基底噪声，当部分频带干扰影响系统时，白噪声的影响较弱，误码率的性能主要受部分频带干扰影响，但当信干比较大时，干扰的影响减弱，则呈现白噪声的影响，不同信噪比的误码率下限不同。

同时，干扰时间占比所引起的误码率变化，主要影响在干扰有效作用时，由于干扰时间占比减小，而误码率有所提高，但当信干比较大时，干扰失去了影响，干扰时间占比也无法改变误码率性能。为便于分析干扰的影响，以下均考虑背景白噪声的信噪比为10 dB。

5.2　抗部分频带干扰的性能仿真

考察FH/OFDM系统，OFDM的子载波数为84，分别考虑部分频带干扰因子ρf为0.1、0.3、0.5以及时间窗口因子ρT为1/2、2/3、1时的误码率关系，信噪比为10 dB。其中，部分频带干扰由噪声序列产生，其强度由信干比控制，经过IFFT变换，获得干扰时域波形，再经过时间窗口选择干扰时间窗，经过蒙特卡洛法仿真得到的误码率曲线如图5所示。

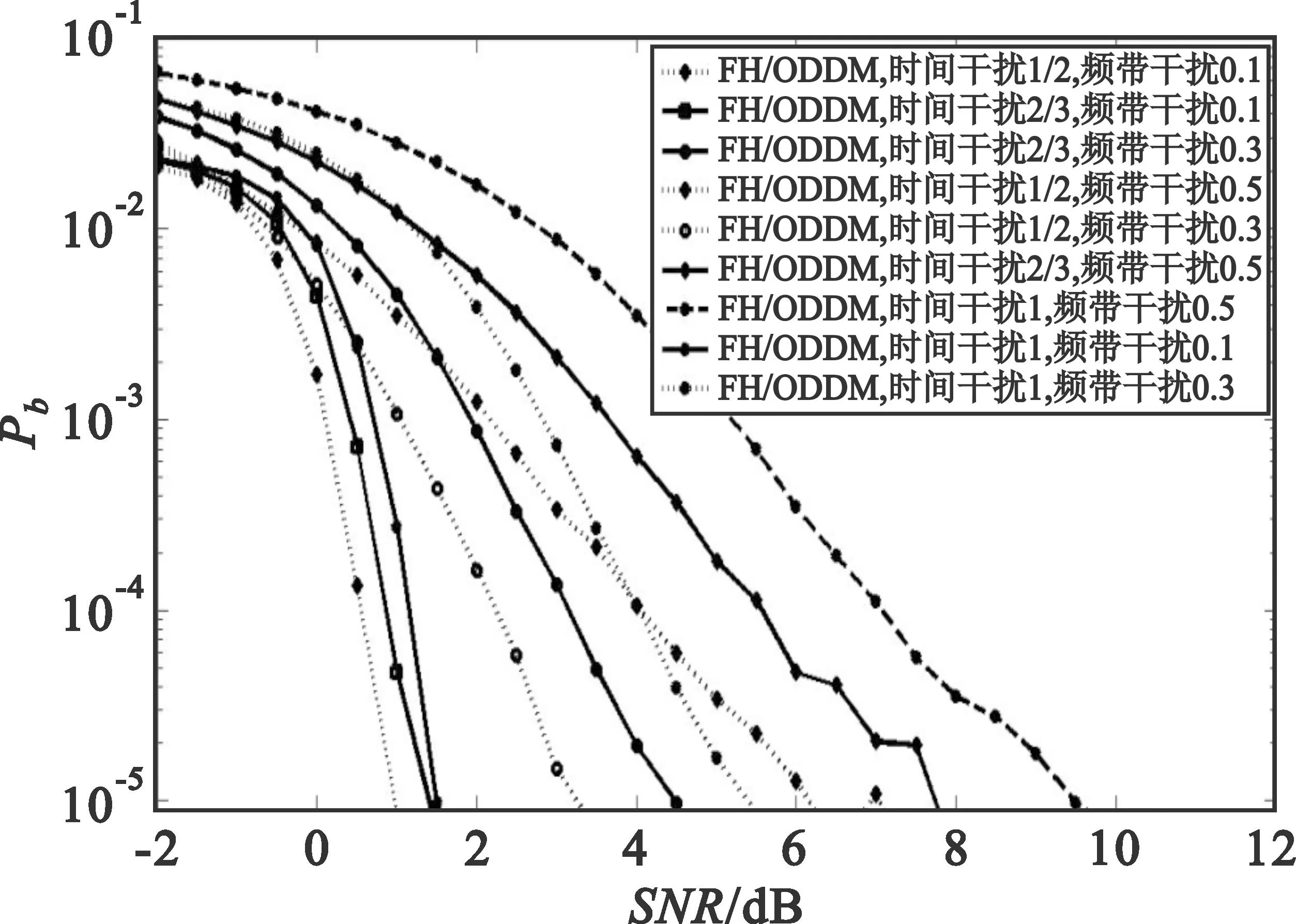
图5　FH/OFDM系统部分频带干扰、时间干扰窗口

根据仿真结果可以看出：部分频带干扰因子越大，系统所受影响越大；干扰时间窗口对误码率的影响，与部分频带干扰因子和信干比有关，如在ρf=0.1时，处于低信干比，此时，干扰时间窗口的影响并不大；而在ρf=0.5时，在高信干比条件下，误码率性能恶化2 dB左右；在部分频带干扰与部分时间干扰之间存在等效的效果区域，如ρf=0.5、ρT=1/2与ρf=0.3、ρT=1在信干比为4 dB时，误码率相等，而在信干比小于4 dB时，前者的误码率优于后者，而在信干比大于4 dB时，后者的误码率优于前者。

5.3　抗多音干扰的性能仿真

仿真条件为84路OFDM子载波，信噪比为10 dB，多音干扰因子ρf为0.1、0.3，时间干扰窗口ρT为1/2、2/3、1。其中，多音干扰取自于信号序列的一部分，经过噪声序列控制的相位以及噪声序列控制的幅度获得多音干扰序列，其幅度强度由信干比控制，经过IFFT变换，获得干扰时域波形，再经过时间窗口选择干扰时间窗，经过蒙特卡洛法仿真得到多音干扰时的误码率曲线如图6所示。

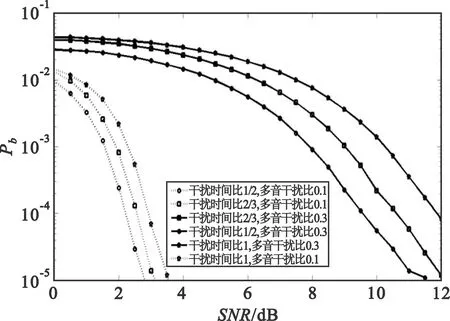
图6　FH/OFDM系统多音干扰、时间干扰窗口与误码率关系

根据仿真结果可以看出:多音干扰因子越大，系统所受影响越大，当多音干扰因子达到0.5时，误码率仅0.5，为严重干扰状态；干扰时间窗口对误码率的影响与多音干扰因子和信干比有关，如在ρM=0.1时干扰时间窗口大小的影响要小于ρM=0.5时的影响；误码率达到10-5时，若ρM=0.1，干扰时间窗口的影响在0.5 dB左右，而在ρM=0.5时，其影响在2 dB左右。

6结束语

本文针对短波FH/OFDM通信系统在中低速跳频条件下跟踪干扰将成为典型的干扰模式，通过仿真研究获得了不同信干比时最佳跟踪干扰的干扰时间比，并对常见的部分频带和多音跟踪干扰的性能进行了分析，仿真结果表明：部分频带干扰因子越大，系统所受的影响越大，同时跟踪干扰时间窗口对系统的影响还与信干比有关；部分频率干扰与部分时间干扰之间存在等效区域；多音干扰对系统的影响与干扰因子密切相关，但在同样信干比条件下，针对OFDM符号的多音干扰影响要远大于部分频带干扰的影响。因此，跳频与OFDM技术的结合，通过高速载波跳频，减小干扰对OFDM符号的影响，也是消除多音干扰的重要手段。

参考文献：

[1]征惠玲.国外无线通信抗干扰技术研究进展[J].电讯技术,2014,54(4):524-528.

ZHENG Huiling.Research Progress of Anti-Jamming Technology for Wireless Communications[J].Telecommunication Engineering,2014,54(4):524-528.(in Chinese)

[2]单超,王娜,王萍.OFDM系统的抗干扰性能研究[J].系统仿真学报,2006,18(6):1618-1622.

SHAN Chao,WANG Na,WANG Ping.Research of Antijamming Performance About OFDM in Case of Pefect Synchronizations[J].Journal of System Simulation,2006,18(6):1618-1622.(in Chinese)

[3]Luo Jun,Andrian J H,Zhou Chi.Bit Error Rate Analysis of Jamming for OFDM Systems[C] //Proceedings of 2007 Wireless Telecommunications Symposium.Pomona,CA:IEEE,2007:1-8.

[4]濮荣强,沈林放.OFDM跳频载波的抗干扰性能研究[J].山东理工大学学报(自然科学版),2011,25(3):36-38.

PU Rongqiang,SHEN Linfang.Studies of the anti-jamming performance of OFDM frequency hopping carriers[J].Journal of Shandong University of Technology(Natural Science Edition),2011,25(3):36-38.(in Chinese)

[5]Abdelhakim M, Ren Jian, Li Tongtong.Reliable OFDM System Design under Hostile Multi-tone Jamming[C] //Proceedings of 2012 IEEE Global Communicdations Conference(GLOBECOM).Anaheim,CA:IEEE,2012:427-4295.

[6]Shan Chao,Wang Ping,Sun Guozhong.Performance of OFDM in the Presence of Multitene Jamming[C] //Proceedings of 2012 IEEE International Symposium on Robotics and Applications.Kuala Lumpur:IEEE,2012:118-121.

[7]Proakis J G.Digital Communicationgs [M].4th ed.Beijing:Publishing House of Electronics Industry,2009.

[8]Clancy T C.Efficient OFDM denial:Pilot jamming and pilot nulling[C] //Proceedings of 2011 IEEE International Conference on Communications.Kyoto:IEEE,2011:1-3.

[9]Han M,Yu T,Kim J.An Efficient Channel Estimation Algorithm under Narrow-Band Jamming for OFDM Systems[C]//Proceedings of 2006 Military Communications Conference.Washington DC:IEEE,2006:1-6.

[10]Han M,Yu T,Kim J.OFDM Channel Estimation With Jammed Pilot Detector Under Narrow-Band Jamming[J].IEEE Transactions on Vehicular Technology,2008,57(3):1932-193.

[11]Park J,Kim D,Kang C.Effect of Bluetooth Interference on OFDM-based WLAN[C] //Proceedings of 2003 IEEE 58th Vehicular Technology Conference.Jeju,Korea:IEEE,2003:786-789.

[12]Patel C S,Stuber G L,Pratt T G.Analysis of OFDM/MC-CDMA under imperfect channel estimation and jamming[C] //Proceedings of 2004 IEEE Wireless Communications and Networking Conference.Atlanta Georgia:IEEE,2004:952-958.

甘海慧(1975—)，女，湖北武汉人，硕士，高级工程师，主要从事通信系统与网络设备测试工作;

GAN Haihui was born in Wuhan,Hubei Province,in 1975.She is now a senior engineer with the M.S. degree.Her research concerns system test for communication and network equipment.

Email:553533679@qq.com

熊俊俏(1966—)，男，湖北天门人，博士，教授，主要研究方向为无线通信系统与无线传感器网络应用;

XIONG Junqiao was born in Tianmen,Hubei Province,in 1966.He is now a professor with the Ph.D. degree.His research concerns wireless communication system and application of wireless sensor network.

Email：305388096@qq.com

曹新莉(1977—)，女，陕西西安人，博士，副教授，主要研究方向为无线通信系统与通信信号处理;

CAO Xinli was born in Xi'an,Shaanxi Province,in 1977.She is now an associate professor with the Ph.D. degree.Her research concerns wireless communication system and communication signal processing.

Email：6909753@qq.com

陈爱杰(1991—)，男，湖北荆州人，硕士研究生，主要研究方向为无线通信系统。

CHEN Aijie was born in Jingzhou,Hubei Province,in 1991.He is now a graduate student.His research concerns wireless communication system.

Email：513751897@qq.com