离散采样偏差造成的信噪比损失分析与改善*

陈　娟

(中国西南电子技术研究所，成都 610036)

离散采样偏差造成的信噪比损失分析与改善*

陈娟**

(中国西南电子技术研究所，成都 610036)

摘要：分析了离散采样偏差造成的目标信噪比损失，提出采用幅度最大原则搜索获得采样位置偏差值，利用该偏差值在频域完成对采样偏差的补偿，从而改善信噪比的损失。讨论了该算法的应用条件，分别对强散射点目标和弱散射点目标情况进行了仿真，分析了随着信噪比变化该算法对信噪比损失改善的效果，验证了算法的有效性。算法具有较低的运算复杂度，因而在实际系统中易于实现。

引用格式：陈娟.离散采样偏差造成的信噪比损失分析与改善[J].电讯技术，2015,55(2):206-210.[CHEN Juan.Analysis and Compensation of Signal-to-Noise Ratio Loss Caused by Discrete Sampling Offset[J].Telecommunication Engineering,2015,55(2):206-210.]

关键词：雷达信号处理；离散采样偏差；信噪比损失；幅度最大补偿法

中图分类号：TN957.51

文献标志码：码：A

文章编号：号：1001-893X(2015)02-0206-05

收稿日期：*2014-09-05；修回日期：2014-12-08Received date:2014-09-05；Revised date：2014-12-08

通讯作者：*chj1030@163.comCorresponding author：chj1030@163.com

Abstract：The signal-to-noise ratio(SNR) loss caused by discrete sampling offset is analyzed.Amplitude optimization compensation algorithm is proposed for reducing the SNR loss.Firstly,based on amplitude optimization,the sampling offset range is searched.And then the SNR loss is compensated by the sampling offset range in frequency domain.The applied condition is discussed.The simulation of high SNR target and low SNR target shows the compensation result of the algorithm in different SNR,which proves its effectiveness.The proposed algorithm is suitable for practical system with low computational complexity.

作者简介：

Analysis and Compensation of Signal-to-Noise Ratio Loss Caused

by Discrete Sampling Offset

CHEN Juan

(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

Key words：radar signal processing;discrete sampling offset;signal-to-noise ratio loss;amplitude optimization compensation algorithm

1引言

随着现代雷达轻小型化发展，使用较小的发射功率探测到更远距离的目标成为雷达应用中的迫切需求，这使得尽量降低信号处理信噪比损失，即提高信噪比成为一个重要的研究内容。

实际中常采用长时间相参和非相参处理进行信号积累提高目标信噪比，实现的方法包括包络移动补偿[1-2]、Keystone变换[3-5]、时频积累[6-7]、空时积累[8]等各种算法。这些算法虽能将不同采样时刻的目标位置对齐后进行积累，但均未考虑实际系统中由于离散采样偏差造成的信噪比损失。

本文分析了实际雷达信号处理中由于离散采样偏差造成的信噪比损失，提出了采用幅度最大准则搜索获得采样位置偏差值，在频域补偿后使得目标能量聚焦在一个距离单元采样点上，从而改善信噪比的幅度最大补偿法。同时，分析了算法应用的条件，提出了对于不同信噪比目标数据的处理方式，并讨论了运算复杂度。对不同类型目标的仿真结果验证了算法的有效性，因而具有一定的实用价值。

2离散采样偏差造成的信噪比损失分析

考虑系统发射线性调频信号，且探测目标长度未超过距离分辨单元的一半，不考虑电磁波传播衰减对其幅度的影响和窗函数调制，则对于一个相参处理间隔(Coherent Process Interval,CPI)内一个脉冲周期时间(Pulse Recurrent Time,PRT)的目标回波信号形式为

(1)

式中，γ为信号的调频斜率，t为时间；R(t)=R0-vt为目标至雷达瞬时距离，R0为雷达发射信号时刻目标和雷达间距离；v为雷达和目标间的径向速度，相向方向为正；λ为发射信号波长。

由于在此仅考虑采样偏差影响，因此假定雷达和目标间相对速度v较小，在雷达发射信号至收到目标回波的时间段内包络变化可忽略，经线性距离走动校正和距离压缩后，信号形式为

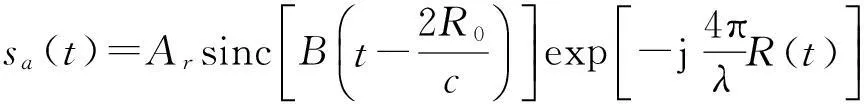
(2)

式中，Ar为脉压后幅度，B为信号带宽，sinc(a)=sinπa/(πa)。

实际系统为离散系统，对于离散系统式(2)改写为

(3)

式中，na和nr分别为脉冲重复频率(Pulse Recurrent Frequency,PRF)采样点和发射信号采样点，与时间轴关系为tn=na·Δta+nr·Δtr，Δta为脉冲重复时间间隔；Δtr=1/fs为采样时间间隔，fs为采样频率；R(naΔta;R0)=R0+vnaΔta为每个PRT时刻目标至雷达的斜距。

在此认为距离走动校正已将不同采样时刻的目标回波包络对齐，即仅考虑由于离散采样造成的目标跨距离单元信噪比损失，因此仅需考虑式(3)的sinc函数项，如式(4)所示：

(4)

从上式可知，当nrΔtr-2R0/c=0时，a(nr)=1，此时幅度最大。而由于离散采样，存在量化误差，最大为Δtr/2，即nrΔtr-2R0/c=Δtr/2。将此误差代入式(4)得到

(5)

从式(5)可知，当fs=B时，该误差最大，为0.64，可见由离散采样造成的跨距离门误差最大可能带来约3.9 dB的损失，而实际系统中采样频率fs应大于带宽B。如取fs=1.2B，则损失约为2.6 dB，如图1所示。

图1　采样偏差造成的信噪比损失

3幅度最大法补偿采样偏差

由于实际系统中，对于大带宽的信号不可能采用高倍率的采样频率，因此有可能存在最大约2.6 dB的采样量化误差，而降低该量化误差的方法唯有使得目标位于离散采样的距离单元上。可采用快速搜索的方法获得距离采样偏差量，然后根据采样偏差量调整采样单元位置，使得目标能量聚于一个距离单元上，从而降低目标位置跨距离单元造成的信噪比损失。

对于波束中仅有一个目标的情况，采用最大幅度搜索方法搜索采样偏差量是最直接和有效的。

3.1　幅度最大补偿法原理

幅度最大补偿法的基本原理在于，当目标恰好位于距离单元采样点时(Δar=0)其幅度最大，相反如目标位置跨距离单元时(Δar≠0)，则其幅度相应较小。以幅度最大为目标，从初始的采样偏差开始迭代搜索，直至最小迭代步长或最大迭代次数，最终获得准确的采样偏差量。

参考式(4)，对于斜距位于R0的目标，完成脉压和走动校正后的距离频域信号表达式如下：

(6)

根据每次迭代的采样偏差量ΔRi，在频域乘该偏差量对应的相位校正因子

(7)

式中，i=1,2，…,N,N为最大迭代次数。则有

(8)

再进行IFFT处理后得到

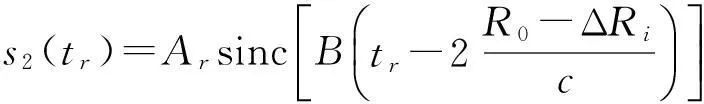
(9)

对于上式中的第二部分，离散采样表达式为

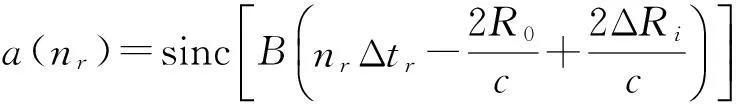
(10)

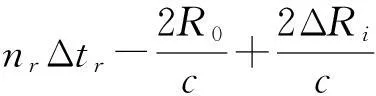
3.2　流程图

幅度最大补偿法流程图如图2所示。

图2　幅度最大补偿法流程图

处理流程如下：

(1)取当前积累周期内完成脉冲压缩和走动校正后的距离频率信号，设置初始距离偏差迭代量ΔR0；

(2)根据初始迭代偏差量计算频域相位校正因子；

(3)将相位因子与频域信号相乘，并完成IFFT处理，获得最大幅度值，记为A0；

(4)根据偏差步长获得ΔRi，循环步骤2~3，将得到的Ai与Ai-1比较，如Ai>Ai-1则ΔRi+1=ΔRi+ΔRstep，否则步长减半，符号取反；

(5)当迭代步长小于设置的最小迭代步长，或者达到了设置的最大迭代次数时，完成整个搜索过程；

(6)使用搜索得到的采样偏差进行补偿，使得目标聚焦于一个距离单元采样点。

此外，迭代步长和迭代次数设置原则如下：

(1)为了尽量减小迭代次数，初始迭代步长设置为距离采样间隔的一半；

(2)从式(5)和图1可知，由于当采样频率达到带宽的6倍时，采样偏差造成的误差已降低至0.1 dB，因此最小迭代步长可设置为采样间隔的1/8即可；

(3)最大迭代次数可根据对运算量的要求进行设置。

4仿真分析结果

作为对上述理论的验证，在此参考实际系统参数对算法进行仿真分析。该理论主要基于对空探测情况，因此并未引入地杂波的影响。

仿真参数设置如表1所示。

表1　仿真参数表

由于采用幅度为标准进行搜索，在此对不同信噪比的目标进行了仿真分析，以验证其有效性。

4.1　不同信噪比时幅度最大补偿法效果

图3为对于不同信噪比情况下采用最大幅度搜索得到离散采样偏差值，根据偏差值调整采样位置后的信噪比损失结果。

图3　不同信噪比时幅度最大补偿法效果

从图3中可知，当目标信噪比大于等于7 dB时，幅度最大补偿法获得的距离采样偏差可改善信噪比损失低于0.1 dB；当目标信噪比位于3~7 dB时，该方法改善信噪比损失低于0.2 dB；当目标信噪比低于3 dB时，该方法改善信噪比损失下降明显，0 dB时仅为1.2 dB；而当目标信噪比为负时，以最大幅度搜索已无法正确搜索到目标，因此需采用其他算法提高采用最大搜索法前的目标信噪比。

由以上分析可知，如果系统要求采样偏差造成的信噪比损失分别低于0.1 dB和0.2 dB，幅度最大补偿法的应用前提为处理的数据中目标信噪比需达到7 dB和3 dB以上。

4.2　强散射点目标仿真

图4和图5为仿真分析得到的对于强散射点目标距离走动校正后跨距离单元以及经过幅度最大补偿法得到的不跨距离单元情况的二维图像。仿真结果表明，幅度最大补偿法对于高信噪比目标有很好的聚焦改善效果，且不跨距离单元时的幅度相比跨距离单元时的幅度约2.615 dB，与式(5)分析一致。

(a)处理前跨距离单元二维图

(b)处理后不跨距离单元二维图

图5　强点目标跨距离单元与否的幅度剖面

4.3　弱散射点目标仿真

对于弱散射点目标，脉压后的数据中目标可能被噪声淹没，此时使用幅度最大原则搜索采样偏差将失效，需对弱目标脉压后的数据进行相参积累等处理，增强信噪比后采用幅度最大补偿算法。对于信噪比为-15 dB的信号，经128个PRT的相参积累后幅度最大补偿算法的处理结果如图6所示。

图6　弱点目标相参积累后跨距离单元与否的幅度剖面

从仿真结果可见，对于弱散射点目标在积累后采用幅度最大补偿法可得到很好的聚焦效果，能改善目标由于采样偏差造成的信噪比损失。

4.4　运算量分析

幅度最大补偿算法中最耗时的应为搜索迭代运算，因此迭代运算中处理的数据量和迭代运算的次数决定了该算法的运算量大小。

对于高信噪比目标，由于脉压后单帧数据的信噪比足够高，满足幅度最大补偿法的应用前提，因此迭代运算处理的数据为脉冲压缩后CPI中的单帧数据。

对于低信噪比目标，由于单帧数据的信噪比不够，因此需对积累后的数据进行搜索处理，但迭代运算处理的数据量同样只有一帧数据。

在仿真中设置初始迭代步长为1/2采样单元，最小迭代门限为1/8的采样单元，以2分法原则进行迭代搜索，所需迭代次数为5次。

综上所述，完成幅度最大补偿算法的搜索迭代运算仅需对单帧数据进行5次迭代运算，可见运算量很小。

5结束语

本文分析了实际雷达信号处理中由于离散采样偏差造成的目标跨距离单元的信噪比损失，提出采用幅度最大补偿法搜索获得采样位置偏差值，补偿后使得目标能量聚焦在一个距离单元采样点上，从而降低信噪比损失。

对不同信噪比情况下的数据进行了仿真验证，结果表明对于3 dB以上信噪比的数据，可以得到低于0.2 dB的损失。分别对未进行积累的强点目标数据和进行相参积累后的弱目标数据采用该算法进行处理均达到很好的效果。

该算法的运算量很小，仅需对单帧数据进行5次迭代运算，易于在实际系统中实现，具有较高的实用价值。

参考文献：

[1]王俊，张守宏.微弱目标积累检测的包络移动补偿方法[J].电子学报，2000，28(12):56-59.

WANG Jun,ZHANG Shouhong.Study on the Motion Compensation of Range Migration for Weak Moving Target Detection[J].Acta Electronica Sinica,2000，28(12):56-59.(in Chinese)

[2]庞存锁,侯慧玲.基于包络补偿的高速多目标检测算法[J].弹箭与制导学报,2013,33(3):163-170.

PANG Cun suo,HOU Huiling.High Speed Multi-target Detection Based on Envelope Migration Compensation[J].Journal of Projectiles，Rockets，Missiles and Guidance,2013,33(3):163-170.(in Chinese)

[3]TIAN Jing,CUI Wei,SHEN Qing,et al.High-speed maneuvering target detection approach based on joint RFT and keystone transform[J].Science China(Information Sciences),2013(6):93-105.

[4]张顺生,曾涛,基于Keystone变换的微弱目标检测[J].电子学报，2005,33(9):1675-1678.

ZHANG Shunsheng,ZENG Tao.Weak Target Detection Based on Keystone Transform[J].Acta Electronica Sinica,2005,33(9):1675-1678.(in Chinese)

[5]Perry R P,Dipietro R C,Fante R L.SAR imaging of moving target [J].IEEE Transactions on Aerospace and Electronic System,1999,35(1):188-200.

[6]李品,刘振星,黄健.跨距离门目标的时频积累及检测方法研究[J].现代雷达，2012,34(8):52-54,80.

LI Pin,LIU Zhenxing,HUANG Jian.A Study on Hybrid Integration and Detection for Range Migration Target Based on Time-frequency Method[J].Modern Radar,2012,34(8):52-54,80.(in Chinese)

[7]ChenV C,Qian S.Joint time-frequency transform for radar range-Doppler imaging [J].IEEE Transactions on Aerospace and Electronic System,1998,34(2):1-5.

[8]樊玲.多帧相参积累检测前跟踪方法[J].电讯技术,2011,51(7):50-54.

FAN Lin.Track-before-detect Method Based on Coherent Integration during Multi-scan[J].Telecommunication Engineering,2011,51(7):50-54.(in Chinese)

陈娟(1984—),女，湖北石首人，2008年于电子科技大学获硕士学位，现为工程师，主要研究方向为雷达信号处理。

CHEN Juan was born in Shishou,Hubei Province,in 1984.She received the M.S. degree from University of Electronics Science and Technology of China in 2008.She is now an engineer.Her research concerns radar signal processing.

Email:chj_1030@163.com