工作点驱动的模拟集成电路优化设计

陈　晓，郭裕顺

(杭州电子科技大学信息工程学院，浙江 杭州 310018)



工作点驱动的模拟集成电路优化设计

陈晓，郭裕顺

(杭州电子科技大学信息工程学院，浙江 杭州 310018)

摘要：工作点驱动的电路优化设计以电路直流工作点上一组独立的器件电压、电流作为优化变量。实现这一方法需要根据器件的工作点电压、电流确定器件尺寸。提出了用T-S模糊逻辑建立器件尺寸与工作点之间关系模型的方法，由此可准确、高效地完成直流工作点的设计，并开展进一步的优化。采用这一模型，以一个两级运算放大器为例，给出了工作点驱动优化设计的结果。

关键词：模拟集成电路；优化设计；工作点驱动；模糊逻辑

0引言

通常的电路优化设计都是以电路中的元器件参数作为设计变量的。对CMOS集成电路，一般是MOS管的几何尺寸，即沟道长度L与宽度W。采用常用的优化算法，优化过程中这些长、宽参数的变化虽可限制在一定的范围内，但其具体取值是不可预测的，常常出现一些极不合理的值，使电路远离正常工作状态，或出现仿真计算过程中的不收敛，导致优化过程过早终止。为此，近年来出现了工作点驱动的优化设计方法[1-3]，这种方法以电路直流工作点上的一组独立的电压、电流作为变量来进行优化设计，可以避免以上问题。同时由于改变了电路的设计空间，还具备某些独到的优点。

实现工作点驱动的优化，要解决的首要问题是如何从器件的工作点电压、电流获得器件尺寸及各种电参数。对长沟道器件，根据平方律模型，器件长宽可从其工作点电压电流立即求得；但对目前大多数情况下的小尺寸MOS工艺设计，简单的平方律模型无法满足精度要求，本文为此提出用模糊逻辑建模的方法来完成这一任务。先利用HSpice等电路模拟器中内置的高精度MOS模型获得一组样本数据，再应用T-S模糊逻辑系统建立器件尺寸与工作点电压电流之间的关系模型，优化过程中直接调用这一模型，就可从器件端电压电流立即确定器件参数。在此基础上，可较为方便地实现工作点驱动的MOS集成电路优化。

1工作点驱动的电路优化设计

通常一个电路的优化设计问题可表达为：

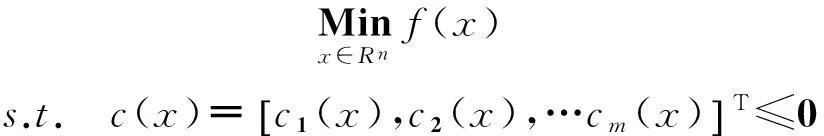
(1)

式中，x为设计变量，f(x)为目标函数，c(x)为约束条件。对CMOS电路，设计变量x一般是各MOS管的长度与宽度，目标函数是功耗、面积与速度、带宽等要优化的性能指标，约束条件是电路的工作状态(如MOS管工作在饱和区)要求及部分约束性电路指标要求。一般电路的性能指标与尺寸参数之间的关系较为复杂，要先求解电路的直流工作点，再根据工作点上的小信号交流参数进行计算。在基于方程的优化中，性能参数通过近似解析表达式计算；在基于仿真的优化中，性能参数则通过调用SPICE等电路仿真器计算。对小尺寸工艺，为了保证计算精度，往往只能采取后者。但在优化过程中经常会出现某次迭代的x对应的电路远离正常工作区域，部分MOS管不是工作在饱和区甚至不能导通，或在求解直流工作点时就不收敛，导致优化过程无法进行下去。

反观传统的手工设计方法。MOS电路的手工设计通常包含如下几个步骤[4]：1)给电路中每一个晶体管设置合适的过驱动电压和偏置电压；2)确定电路的功耗及电源电压，然后由总电流合理分配主要支路的电流；3)对电路的其它性能参数加以约束直到电路中各MOS管的电流和电压都确定下来，再用MOS管的平方律模型计算出所有器件的长宽比；4)调用Hspice等电路仿真器对设计进行调整、验证，这通常需要反复迭代。由于这一过程的出发点是各MOS管的工作电压与电流，因此可称之为工作点驱动的设计方法。

工作点驱动的优化设计即模仿手工设计过程，将优化的变量从器件尺寸W、L改作电路中一组独立的器件端电压、电流。对一个MOS管，从端电压电流可求出其尺寸参数，如对长沟道器件有：

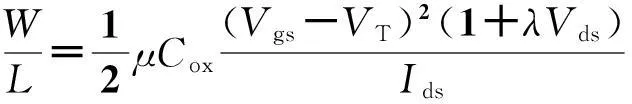
(2)

式中，Vgs为MOS管的栅源电压，Vds为漏源电压，Ids为漏电流，μ、Cox为工艺常数，λ为沟道长度调制系数。可见确定的工作点电压电流对应一个确定的器件，因此可选择一组独立的电压电流作为电路的决定参数。

设计参数改变后，首先不再需要计算电路的直流工作点，避免了以尺寸参数作为变量时工作点可能不正常的问题；其次由于改变了电路的设计空间，可方便地表达设计时对电路工作区域的约束(即约束方程)；此外，还可能使优化变量与目标函数之间的映射关系变得更为简单，有利于优化算法的收敛。同时，由于更接近于传统手工设计，可使设计者更好地理解设计过程与设计结果，也为优化过程结合设计者已有的经验提供了可能。

2器件尺寸的模糊逻辑建模

实现上述工作点驱动的优化设计，必须要有依据器件电压电流决定尺寸的方法。对短沟道器件，式(2)的误差太大，而精确的模型方程

IDS=f(VGS，VDS，VBS，W，L)

(3)

如BSIM、EKV等均较为复杂，难以得到类似式(1)的简便计算式。本文采用数值建模的方法来完成这一任务，先用模糊逻辑构造出如下模型：

W=f(IDS，VGS，VDS，VBS，L)

(4)

设计时调用这一模型，从由器件电压电流求出宽度。对短沟道器件，由于尺寸对特性的影响不只由长宽比决定，因此上述模型中L是自变量。设计时沟道长度一般可事先确定。

一个模糊逻辑系统由一组模糊推理规则组成，规则表示的是输入与输出变量之间的关系[5]：

ifx1isA1，x2isA2，…，xn isAntheny=B

(5)

式中，x1，x2，…，xn为输入变量，A1，A2，…，An为输入变量的模糊子集，y为输出变量，B为输出变量的取值。本文采用Sugeno模糊逻辑模型，其结论部分可以是任意非线性函数，即将式(5)中的B取作f(x1，x2…，xn)，通常f是输入变量x1，x2，…，xn的一个多项式。每一条如式(5)所示的推理规则会产生一个输出量y，将所有推理规则输出的y进行加权平均后得到系统最后的输出：

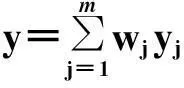
(6)

式中，w为权重，由各模糊集的隶属函数决定，yj为结论部分的多项式函数。式(6)即是模糊逻辑模型的表达式。根据建模对象的一组输入与输出训练样本，可建立这样的模糊逻辑模型，具体过程参考文献[5]，这里不再赘述。

对TSMC 0.35 μm工艺库，上述模型的结果如下：选取不同的器件端电压VGS、VDS、VBS组合，通过Hspice中内建的Bsim3v3模型仿真获得IDS的准确值，然后代入模型并与事先设置的W值进行比较。图2给出了较窄与较宽两种情况下(W=1 μm和W=100 μm)由模型得到的宽度值，横坐标代表不同的组合(样本)次序。可以看出，两种情况下模型的准确度是比较高的，全部样本的平均相对误差在1%以下。更多情况下的测试结果也类似。

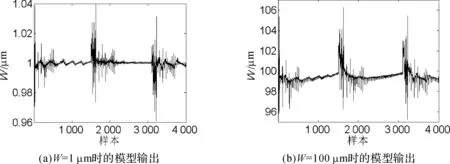
图1　W模型测试输出及误差

3两级运放设计实例

下面以一个带米勒补偿的两级运放为例，说明工作点驱动的优化设计。采用TSMC 0.35 μm工艺，电路的VDD=2.5 V，VSS=-2.5 V，CL=2 PF，性能要求如表1所示，考虑的性能指标为单位增益带宽(UGB)、功耗(Power)、相位裕度(PM)、单位增益(AV)及摆率(SR)。

表1　运放性能参数要求

先进行工作点驱动的初始设计。取电路偏置电流Ibias为15 μA，M5的尾电流为15 μA，M7的尾电流为60 μA，CC=1 PF，这样流过M1、M2分别为7.5 μA。根据各器件都在饱和区域工作的条件，设置各工作电压情况如下：Vgs1=Vgs2=0.7 V，Vgs3=Vgs4=Vgs6=-0.9 V，Vgs5=Vgs7=Vgs8=0.7 V，Vds1=Vds2=2.3 V，Vds3=Vds4=-0.9 V，Vds5=1.8 V，Vds6=-2.5 V，Vds7=2.5 V，Vds8=0.7 V，Vsb，i=0，i=1，2，…，10。取MOS管的长度L=1 μm。根据设置好的电路工作点，运用上述W尺寸的模糊逻辑模型，求得各MOS管的宽度尺寸W的值，如表2所示。

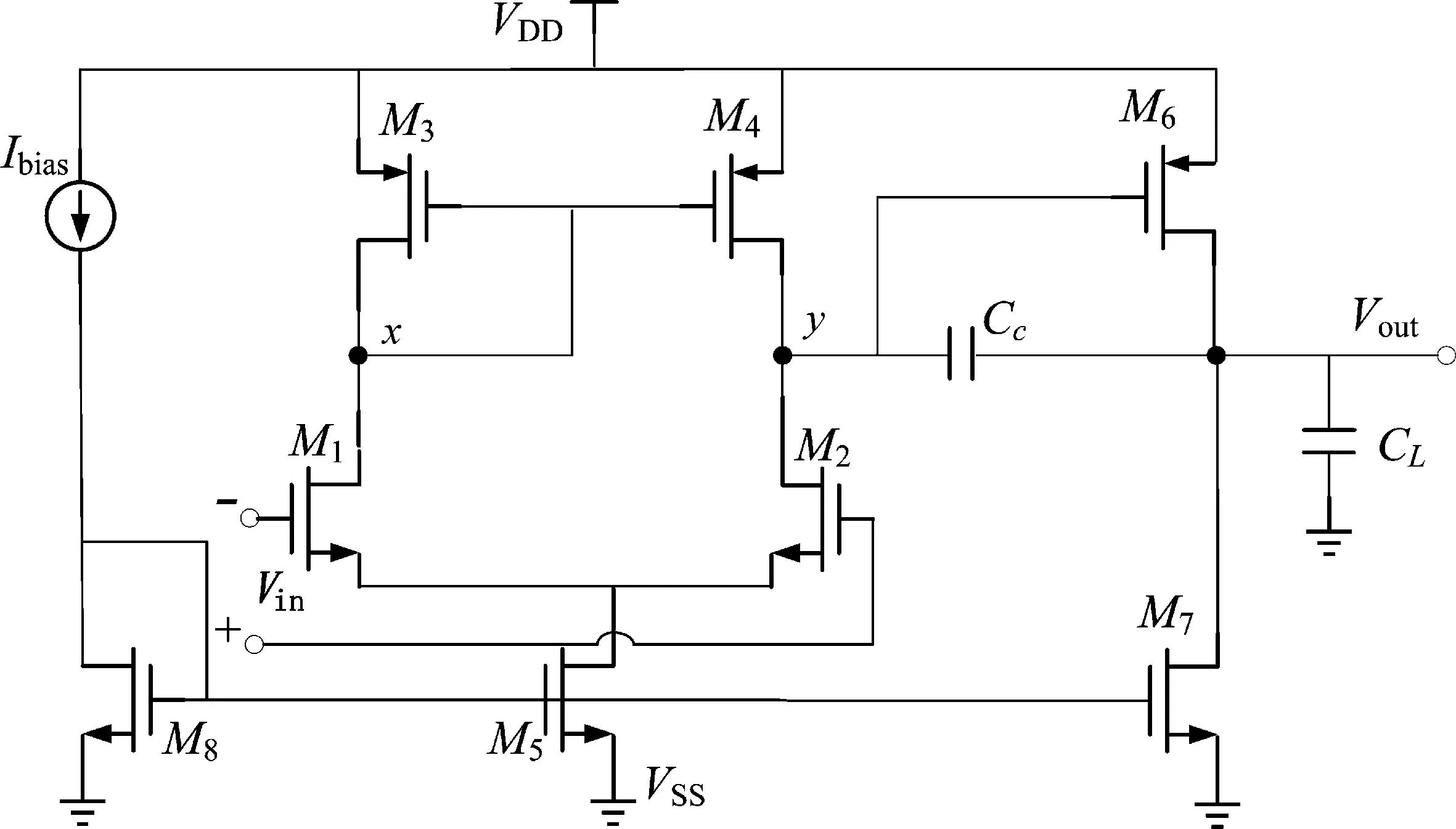
图2　CMOS两级运算放大器电路

μm

可以用Hspice检验得到的电路是否满足开始设置的工作点，验证结果如表3所示。表3中，期望值为设置的各电压电流，数值模型为采用模糊逻辑模型所得结果，平方律模型为采用平方律公式(2)所得结果，从两者的误差值可见按平方律模型设计的工作点误差是较大的。

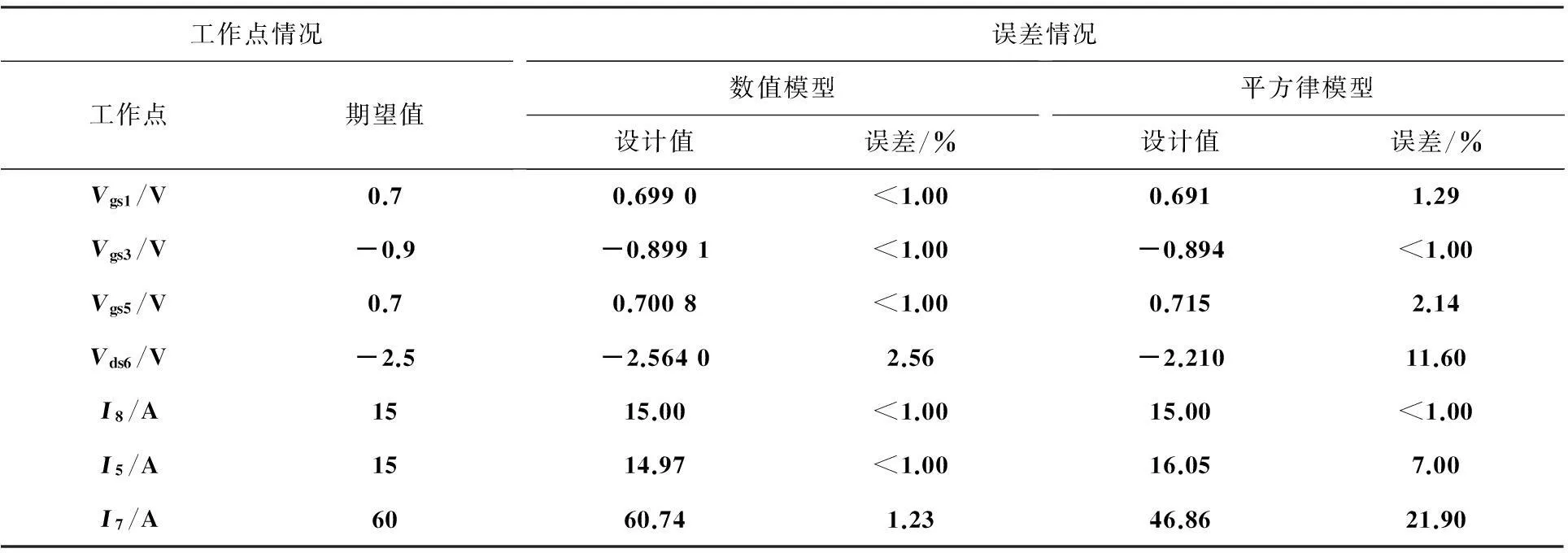
表3　电路工作点情况及误差情况

再根据表2得到的器件W值，用Hspice仿真验证得到的电路各性能参数，结果如表4所示。对照表1的要求，可见相位裕度和带宽还不能满足。

表4　初始设计得到的电路性能

为此对该电路进一步优化，采用matlab工具箱中的约束优化工具fmincon。目标函数为功耗，表1中的其余性能要求作为约束条件，性能参数采用基于方程的计算得到(即采用基于方程的优化[6])，但计算时所用的器件小信号参数不采用长沟道模型对应的参数，而是用上节的模糊逻辑建模建立的小信号参数数值模型，这样保证基于方程的优化也有较好的精度[7]。

优化后的结果如表5，此时得到的各器件尺寸和补偿电容如表6。由于基于方程的优化不能完全消除误差，因此对这样得到的电路最后再用Hspice进行验证校核，结果如表7所示，对照表1所列出的设计指标，可见电路的全部性能指标都已满足要求，并实现了功耗的最小化。

表5　优化后的电路性能

表6　优化设计结果

表7　仿真结果及误差

4结束语

工作点驱动的模拟电路优化设计较通常的方法有不少优点。本文先用模糊逻辑建立器件尺寸与工作点电压电流之间的关系的数值模型，再采用MATLAB中的优化工具箱进行基于方程的优化。电路设计实例表明，这样的数值模型可准确地进行电路工作点设计，在此基础上再进行某一目标的优化，最后得到满意的设计结果。

参考文献

[1]Guerra-Gómez I,McConaghy T,Tlelo-Cuautle E.Operating-point driven formulation for analog computer-aided design[J].Analog Integrated Circuits and Signal Processing,2013,74(2):345-353．

[2]Iskander R,Lou⊇rat M M,Kaiser A.Hierarchical sizing and biasing of analog firm intellectual properties[J].Integration,the VLSI Journal,2013，46(2):172-188．

[3]Liu B，Pak M，Zheng X，et al.A novel operating-point driven method for the sizing of analog IC[C]//Circuits and Systems(ISCAS),2011 IEEE International Symposium on.Rio de Janeiro：IEEE，2011：781-784．

[4]Razavi B.Design of analog CMOS integrated circuits[M].New York：McGraw-Hill,2001：305-306．

[5]Wang L Y，Guo Y S.Large-Signal MOSFET Modeling by Means of Knowledge Based Fuzzy Logic System[C]//ASIC (ASICON),2011 IEEE 9th International Conference on.Xiamen：IEEE,2011：953-956．

[6]Gielen G G E,Rutenbar R.Computer-aided design of analog and mixed-signal integrated circuits[J].Proceedings of the IEEE,2000,88(12):1825-1854．

[7]蒋海晓.CMOS运放多目标优化设计的快速算法[D].杭州：杭州电子科技大学.2013：25-36．

Operating-point Driven Optimal Design of Analog CMOS ICs

Chen Xiao，Guo Yushun

(SchoolofInformationEngineering，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract：Operating-point driven design of analog circuits uses a group of independent device voltages and currents as the design variables.Its implementation need to convert the terminal voltages and currents into the size of the device.A method to realize such a conversion based on T-S fuzzy logic modeling is proposed in this paper.Accurate DC operating-point design is achieved and further circuit optimization can be carried out with this method.A design example of a two-stage operational amplifier is given to demonstrate the effectiveness of the method.

Key words：analog circuits；optimal design；operating-point driven；fuzzy logic

中图分类号：TN402

文献标识码：A

文章编号：1001-9146(2015)06-0018-05

通信作者：

作者简介：陈晓(1989-)，男，浙江嘉兴人，在读研究生，集成电路设计.郭裕顺教授，E-mail：ysguo@hdu.edu.cn．

基金项目：国家自然科学基金资助项目(60672013)

收稿日期：2015-02-05

DOI：10.13954/j.cnki.hdu.2015.06.004