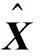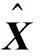一种改进的正则化自适应匹配追踪算法

王芳星，刘顺兰

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

摘要：针对压缩感知中未知稀疏度信号的重构问题，提出了一种改进的正则化自适应匹配追踪算法。它通过自适应变步长迭代对信号稀疏度进行估计，并将其作为初始支撑集长度，然后在分阶段迭代中正则化筛选原子，最终实现信号的精确重构。仿真结果表明，该算法重构信号的性能和效率均优于子空间追踪算法、正交匹配追踪算法和稀疏度自适应匹配追踪算法。

关键词：信号重构；压缩感知；稀疏度；自适应；正则化

DOI: 10.13954/j.cnki.hdu.2015.01.016

一种改进的正则化自适应匹配追踪算法

王芳星，刘顺兰

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

摘要：针对压缩感知中未知稀疏度信号的重构问题，提出了一种改进的正则化自适应匹配追踪算法。它通过自适应变步长迭代对信号稀疏度进行估计，并将其作为初始支撑集长度，然后在分阶段迭代中正则化筛选原子，最终实现信号的精确重构。仿真结果表明，该算法重构信号的性能和效率均优于子空间追踪算法、正交匹配追踪算法和稀疏度自适应匹配追踪算法。

关键词：信号重构；压缩感知；稀疏度；自适应；正则化

DOI:10.13954/j.cnki.hdu.2015.01.016

收稿日期：2014-04-14

通信作者：

作者简介：王芳星(1988-)，男，江西余江县人，在读研究生，压缩感知.刘顺兰教授，E-mail: liushunlan@163.com.

中图分类号：TN911.72

文献标识码：：A

文章编号：：1001-9146(2015)01-0079-05

Abstract:This paper presents a modified regularization adaptive matching pursuit(MRAMP) algorithm for the problem that reconstruct signals with unknown sparsity in compressed sensing. The proposed algorithm adaptively estimates the sparsity with difference steps through stage by stage and set it to the length of the initial support， then gets the accurate target signal by regularization screening of atoms in every stage. Simulation results show that the performance and efficiency of the proposed algorithm is better than subspace pursuit(SP) algorithm， orthogonal matching pursuit(OMP) algorithm and SAMP algorithm.

0引言

压缩感知(Compressive Sensing， CS)理论充分利用了信号的稀疏度来获取和处理信号[1]。重构算法是压缩感知理论的关键技术，其中贪婪算法结构简单，运算少，因此得到很好的运用。正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法[2]是传统的贪婪算法，它在每次迭代中选取一个原子更新支撑集，效率较低。然而，正则化正交匹配追踪(Regularized Orthogonal Matching Pursuit， ROMP)算法[3]在每次迭代过程中选取多个支撑集原子重构信号，其重构速度比OMP算法快。之后出现的子空间追踪(Subspace Pursuit， SP)算法[4]引入了回溯思想，重构复杂度较低。但上述算法必须已知信号稀疏度，而稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit， SAMP)算法[5]不需要稀疏度作为先验信息。本文针对未知稀疏度信号的重构，将SAMP算法的自适应、SP算法的回退筛选和ROMP算法的正则化原子选择相结合，提出了一种改进的正则化自适应匹配追踪(MRAMP)算法并将其与OMP、SAMP和SP算法进行了性能比较。仿真结果表明，MRAMP算法对信号的重构性能和效率优于其它几种算法。

1压缩感知

压缩感知理论的应用需要信号是稀疏或者近似稀疏的，设X是有限长离散时间信号，可看作空间RN内N×1维列向量，假定Ψ={ψ1，ψ2，...，ψN}是RN内一组标准正交基，则信号X可表示为：

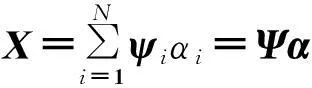
(1)

式中，Ψ为N×N矩阵，α为投影系数[αi]=[〈X，ψi〉]构成的N×1维列向量。可见，X和α是同一个信号的不同表示。如果α中非零元素个数为K(K<

设计一个与变换基不相关的M×N(M

Y=ΦX=ΦΨα=Θα

(2)

式中，Θ=ΦΨ为M×N矩阵，称为恢复矩阵。

2稀疏度估计

本文通过原子匹配测试的方法给出初始稀疏度的估计。下面先给出两个命题。

在SAMP算法中，初始稀疏度设为1或阶段步长取一个较小值，则需要多次匹配、更新、信号估计和残差更新，降低了算法效率。若初始稀疏度随便设为某一常数或取一个较大的阶段步长则会影响算法的精度。针对以上问题，根据命题2可不断增加K0的值来对稀疏度进行初始估计，当条件不满足时，K0为稀疏度初始估计值，同时可得到初始残差和初始阶段步长。

3MRAMP算法

SP算法主要思想是回溯迭代，每次迭代首先计算残差r，然后选择观测矩阵Φ的各个原子φi中与残差最匹配的原子，得到相关系数u：

u={ui|ui=|〈r，φi〉|，i=1，2，…，N}

(3)

将u中最大值对应的索引S并入支撑集索引F，更新支撑集ΦF，并采用最小二乘法进行信号估计以及更新残差：

(4)

(5)

输入：M维测量向量Y，M×N观测矩阵Φ，阶段迭代步长step≠0，δK。

1)初始稀疏度K0=1，稀疏度估计步长step1=step，索引集F0=∅，S=∅(空集)；

2)通过式(3)计算相关系数u，并从u中取出K0个最大值对应的索引值存入索引集F0中；

5)初始化阶段stage=1，初始化迭代次数n=1，初始阶段步长step=「0.5step1⎤，初始支撑集长度size=K0，索引集F=F0；

6)通过式(3)计算u，取出u中size个最大值对应的索引值存入S中；

7)将选出的size个相关系数进行正则化并将得到的索引值存入S0中，然后将S0并入索引集F，更新支撑集ΦF；

图1　MRAMP算法流程图

4算法仿真结果和分析

为了说明MRAMP算法的正确性和有效性，本文采用正弦信号进行实验。

(6)

式中，f1=100 Hz，f2=200 Hz，f3=300 Hz，采样频率fs=800 Hz，ts=1/fs。测量向量长度M=64，原始信号长度N=256，观测矩阵Φ和稀疏变换矩阵Ψ分别取高斯随机矩阵和傅里叶变换矩阵。稀疏度估计步长step1=1，参数δK=0.35，ε=10-6。

MRAMP算法重构信号的仿真结果如图2所示，从图2可以看出该算法能够很好的重构原始信号，并且重构均方误差较小。

图2　MRAMP算法重构信号

M取不同值时，各个算法300次重构实验的平均运行时间如图3所示。由图3可以看出，MRAMP算法的平均运行时间要明显少于OMP算法、SAMP算法和SP算法。

图3　M取不同值时，不同算法的平均运行时间

测量向量长度M=64，高斯白噪声环境中，不同信噪比(Signal Noise Ratio， SNR)下各算法对信号的重构概率如图5所示。由图5可知，各算法的准确重构概率随着信噪比的增大而增大，MRAMP算法的准确重构概率优于SP、OMP、SAMP算法，当信噪比大于10 dB时，所有算法均能准确重构信号。当信噪比为7 dB时，MRAMP、OMP、SAMP和SP算法的重构概率分别为0.780 0、0.720 0、0.594 0和0.682 0，表明同一信噪比下，MRAMP算法的重构概率高于其它几种算法。因此，在噪声环境下，MRAMP算法的重构性能优于OMP、SAMP和SP算法。

图4　不同算法准确重构概率对比

图5　不同信噪比下，信号的重构概率

5结束语

本文在已有的压缩感知重构算法研究的基础上，将信号的稀疏度估计、SAMP算法的自适应、SP算法的回退筛选和ROMP算法的正则化原子选择相结合，提出了MRAMP算法。算法通过原子匹配测试得出初始稀疏度作为初始支撑集长度和小能量残差作为初始残差，减少了整个算法迭代次数，使算法效率得到提高。在变步长分阶段迭代过程中逐渐减小迭代步长并利用正则化选取能量最大的原子来更新支撑集，从而更快更精确地逼近信号稀疏度，当前后两次估计信号的差值达到某一设定的阀值以下便能精确的重构未知稀疏度的信号。仿真结果表明，MRAMP算法重构性能和效率明显优于OMP、SAMP和SP算法。

参考文献

[1]Donoho D L .Compressed sensing[J].IEEE Trans Information Theory,2006,52(4):1 289-1 306.

[2]Tropp J A , Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans on Information Theory,2007,53(12):4 655-4 666.

[3]Needell D , Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics,2009,9(3):317-334.

[4]Dai W , Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J] . IEEE Trans on Information Theory,2009,55(5):2 230-2 249.

[5]DO T T, Lu Gan , Nguyen N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Pacific Grove: IEEE Computer Society,2008:581-587.

[6]杨成,冯魏,冯辉,等.一种压缩采样中的稀疏度自适应子空间追踪算法[J].电子学报,2010,38(4):1 914-1 917.

[7]朱延万,赵拥军,孙兵.一种改进的稀疏度自适应匹配追踪算法[J].信号处理,2012,28(1):80-86.

A Modified Regularization Adaptive Matching Pursuit Algorithm

Wang Fangxing ，Liu Shunlan

(SchoolofCommunicationEngineering，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Key words: signal reconstruction; compressive sensing; sparsity; adaptation; regularization