细胞自动机:简单的规则,复杂的行为
2016-01-22陈芳跃金伟锋
陈芳跃,金伟锋
(1.杭州电子科技大学理学院数学系,浙江 杭州 310018;
2.上海大学理学院数学系,上海 200444)
摘要:细胞自动机是一种时间、空间与状态都离散的数学模型。回顾了初等细胞自动机模型的应用及其符号动力学刻画的相关文献,在大量统计性质和计算机模拟基础上,着重分析具有鲁棒Bernoulli移位特征的细胞自动机规则的一些符号动力学性质,揭示了细胞自动机的简单规则中蕴含着复杂、混沌的非线性动力学特性。这些结果丰富了细胞自动机的理论基础,也将促进符号动力系统的理论和应用的研究。
关键词:初等细胞自动机;规则;符号动力学;混沌;拓扑混合;拓扑熵
DOI: 10.13954/j.cnki.hdu.2015.01.001
细胞自动机:简单的规则,复杂的行为
陈芳跃1,金伟锋2
(1.杭州电子科技大学理学院数学系,浙江 杭州 310018;
2.上海大学理学院数学系,上海 200444)
摘要:细胞自动机是一种时间、空间与状态都离散的数学模型。回顾了初等细胞自动机模型的应用及其符号动力学刻画的相关文献,在大量统计性质和计算机模拟基础上,着重分析具有鲁棒Bernoulli移位特征的细胞自动机规则的一些符号动力学性质,揭示了细胞自动机的简单规则中蕴含着复杂、混沌的非线性动力学特性。这些结果丰富了细胞自动机的理论基础,也将促进符号动力系统的理论和应用的研究。
关键词:初等细胞自动机;规则;符号动力学;混沌;拓扑混合;拓扑熵
DOI:10.13954/j.cnki.hdu.2015.01.001
收稿日期:2014-10-20
基金项目:国家自然科学基金资助项目(11171084)
作者简介:陈芳跃(1956-),男,浙江金华人,教授,数学.
中图分类号:O19;O189.1
文献标识码::A
文章编号::1001-9146(2015)01-0001-09
Abstract:Cellular automata (CA) are mathematical models with discrete time, space and states. Symbolic dynamics is a critical approach and technique for nonlinear dynamical analysis. This work conducts the literature review of investigations of symbolic dynamics of elementary cellular automata and their applications. Based on the extensive statistics properties and exhaustive simulations of elementary cellular automata (ECA), this paper proposes an effective method to unveil symbolic dynamics of Bernoulli-shift rules under the viewpoint of symbolic dynamics in the space of bi-infinite symbolic sequences. These results uncovers the chaotic and complex symbolic dynamics of simple ECA rules, enrich the symbolic dynamics of ECA, and promote the theory and technology of dynamical system, especially symbolic dynamics.
0引言
细胞自动机(Cellular Automata)是时间、空间和状态皆离散的布尔化非线性动力学系统,它由一维、二维或三维的空间规则结构组成,每个细胞都按照相同的规则同步演化,细胞状态由其自身和邻居的状态共同决定[1,2]。作为细胞自动机的最小单位,细胞状态只有有限多个(对于只有两个状态的细胞自动机,其状态常用0和1来表示)。根据具体规则,细胞可以从一个状态转换为另一个状态。自产生以来,细胞自动机模型已被广泛地应用于各个领域[3-6]。在物理学中,细胞自动机成功应用于流体力学的格子气模拟,同时也为热和波动方程等提供简单的模型。在计算机科学中,细胞自动机被用于并行计算的研究[7]。在经济学中,细胞自动机模型成功运用于寡头垄断模型的研究。在非线性科学中,细胞自动机为分形、混沌、分岔、吸引子等动力系统理论的研究提供了有效的模型工具,同时对复杂系统的特征进行有效模拟和描述。因此,细胞自动机的发展一方面得益于离散数学、自动机理论、逻辑数学和图灵机思想等相关理论的研究[8],另一方面也促进了复杂科学、非线性科学等相关学科发展,并导致了人工生命科学的产生[9]。
20世纪50年代计算机创始人John von Neumann正式提出细胞自动机理论,并在Stanislaw Ulam的建议下,于1948年应用于“生物学中的自我复制行为,并且能在计算机上得以实现”的问题研究,建立了一个具有29个状态、具备普适计算能力的细胞自动机。此后,A.W.Burks通过理论研究提出了细胞自动机结构,由于这一结构过于繁复,其发展与应用在当时受到极大限制[10]。由于种种原因,此后关于细胞自动机的探索停滞了约十余年。但随着计算机的普及,J.H.Conway于20世纪70年代编制了一个名为“生命游戏(game of life)”的程序,细胞在网格中生产了稳定和非稳定等难以预测的演化行为。这结果使计算机科学家产生了兴趣,由此细胞自动机的研究再度兴起[11],同时,细胞自动机的符号动力学性质刻画在这时期开始了[12]。1969年Hedlund从数学上严格定义了一维细胞自动机,实质是符号空间上移位映射的自同态。借助此定义,Hedlund详细刻画了具有某些特点细胞自动机(如满射和开射等)的非线性动力学性质。M.A.Shereshevsky(1992年), L.P.Hurd,J.Kari,K.Culi(1992年),G.Lotti, P.Favati,G.Cattaneo,L. Margara,M. Finellt(1997-2000年),F.Ohi (2007,2008年)和H.Akin(2005-2009年)等,相继在符号动力学框架下刻画了具有特殊性质细胞自动机的动力学性质,如加性的、可逆的以及完全的细胞自动机等等[13-18]。除此之外,对其他细胞自动机(尤其是非加性)的符号动力学性质,如拓扑熵、周期轨道、拓扑传递性、拓扑混合性等,知之甚少。
在20世纪80年代,著名学者Stephen Wolfram借助计算机模拟将带有游戏色彩的原始细胞自动机加以分类整理,并使之最终上升到了科学方法论。他建议进一步简化细胞自动机,使其具备简单的局部规则与链接,并具有高度并行计算能力。最简单的一维细胞自动机的状态数为2、左右邻居各为1,被称为初等细胞自动机(Elementary Cellular Automata, ECA)[19,20],它能使计算机反复地计算极其简单的运算规则,并使之发展成为异常复杂的模型,进而解释自然界中的一些复杂和自组织现象。此细胞自动机具有适合超大规模集成电路(VLSI)层次的信息并行处理能力。在大量计算机实验的基础上,Wolfram详细分析了一维细胞自动机的演化行为,将其动力学行为归纳为平稳型、周期型、混沌型、复杂型四大类:(1)自任何初始状态开始,经过一定时间运行后,平稳型的细胞空间趋于一个空间平稳的构形,每一个细胞处于固定状态,不随时间变化而变化(如图1.1所示);(2)周期型的细胞空间趋于一系列简单的固定结构或周期结构,这些结构可看作是一种滤波器(Filter),故可应用到图像处理研究中(如图1.2所示);(3)混沌型表现出混沌的非周期行为,所生成的结构的统计特征不再变止,通常表现为分形分维特征(如图1.3所示);(4)复杂型的出现复杂的局部结构或局部混沌,其中有些会不断地传播,并出现自组织现象(如图1.4所示)。

图1.1 平稳型CA的演化图

图1.2 周期型CA的演化图

图1.3 混沌型CA的演化图

图1.4 复杂型CA的演化图
上述Wolfram的四个分类虽是定性的,但他的研究成果引起了数学家、物理学家等众多学科领域专家的关注,从而使细胞自动机成为研究复杂系统的有效理论模型。由C.Langton提出的人工生命迅速发展成为复杂性科学的一个分支[8]。N.Packard和Langton在进一步深入研究中提出的“混沌的边缘”(the edge of chaos)概念也成为当前复杂性科学研究的重要成果之一[9]。与此同时,细胞自动机的数学理论研究也得到全面发展,特别是在加性细胞自动机、等度连续的细胞自动机以及正扩张的细胞自动机的符号动力学性质方面,取得了一系列完善的研究成果[14,15,21,22]。经过大量的计算机模拟和经验观察,Wolfram在2002年创造性地提出初等细胞自动机是“一种新科学(A New Kind of Science)”[23]。著名学者L.O.Chua等人自2002年开始为Wolfram的初等细胞自动机的计算机模拟结果进行数学刻画,他们结合以往在细胞神经网络(Cellular Neural Networks)和非线性电路等研究方面取得的丰富成果,对细胞自动机开展了系统的研究,在非线性科学杂志International Journal of Bifurcation and Chaos上发表了一系列研究成果(共13篇)[24-36]。他们以周期边界条件的有限长度构形为基本元素,从非线性科学角度系统地揭示了初等细胞自动机内在的一些动力学本质,并发现某些初等细胞自动机可展现如混沌、分形、混沌边缘、遍历、吸引子等非线性科学的几乎所有性质。当然,有部分工作与先前文献重合。如分类问题,文[37]从不同角度也得到了类似结论。
虽然我们可以在不同的框架下研究细胞自动机的动力学性质,然而想得到其演化的普遍性结论依旧十分困难。研究证明,细胞自动机的任何一个非平凡的命题都是不可判定的,即不存在一个可以对所有的细胞自动机作出“是”或“否”的回答的可行算法[38]。因此,对大量的细胞自动机的性质(即使是初等细胞自动机)的严格数学分析仍然是困难而富有挑战性的。近几年来,我们在Hedlund和Chua等研究成果的启发下,结合符号动力学理论和方法,在数学上严格定义了一维细胞自动机——符号空间上的拓扑动力系统,进而对具备某些特征的一维细胞自动机的非线性动力学行为进行了系统地研究,取得了一些成果[39-46,53,57,61-65]。
1细胞自动机与符号动力学
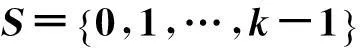
显然上述定义是合理的。称度量空间(SZ,ρ)为一维k符号序列空间,简称一维符号空间,并且是紧致的、完全的、完全不连通的Hausdorff空间。设a=(a0,…ap-1)是S上一个长度为p≥1的有限序列,简称长度为p的字。设x∈SZ,I=[i,j]是一个整数区间,则记x[i,j]=(xi…xj)和x[i,j)=(xi…xj-1),若存在m∈Z,使得x[m,m+p+1]=a,则称“有限序a出现在x内”或“x含有a”,记作az;否则称“有限序列a没有出现在x内”。对于Λ⊆SZ,若存在x∈Λ,使得ax,则称“a出现在Λ内”,仍记为aΛ。设m∈Z,集叫做SZ上的柱集。显然,柱集是既开又闭的,且全体柱集可构成拓扑基,开集为柱集的并。现在,我们SZ上定义移位映射为:则称拓扑动力系统(SZ,σ)为S上的一维符号动力系统。关于(SZ,σ)的动力学性质和部分结论叙述如下[47,48]:
σ有任何周期的周期点;σ的周期点在SZ中稠密;σ拓扑混合⟹σ拓扑传递和对初值敏感依赖;σ的拓扑熵为logk,其中k为符号集S的基数;σ具有Li-Yorke意义下的混沌和Devaney意义下的混沌。
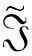
命题1.1任何有限型子移位都与一个2阶有限型子移位拓扑共轭。
由此可知,在诸多有限型子移位中,2阶有限型子移位才是本质的。而且转移方阵是用于刻画2阶有限型子移位动力学行为的主要工具。定义如下:
由符号动力学理论可知,若转移方阵A的每行每列都不全为0,则A和2阶有限型子移位两者之间的可以相互决定。关于2阶子移位ΛA的动力学性质有:(1)σA的拓扑熵为转移方阵A的谱半径;(2)σA是拓扑混合的当且仅当存在正整数N,当n≥N时,An中的每个元素都大于0。
与一般的动力学模型不同,细胞自动机不是由严格定义的物理方程或函数确定,而是由一系列模型构造的规则构成,其特点是时间、空间、状态都离散,每个变量只取有限多个状态,且其状态改变的规则在时间和空间上都是局部的。由此,细胞自动机可以展现复杂而丰富的动力学行为。目前一维细胞自动机的理论研究已有一些结论,而高维的还知之甚少。
从数学的角度,我们可以对一维细胞自动机作如下定义[12]:
定义1.2设f是SZ上的连续映射,若紧致(SZ,f)满足f∘ σ=σ∘ f,则称f是一个一维细胞自动机。
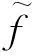
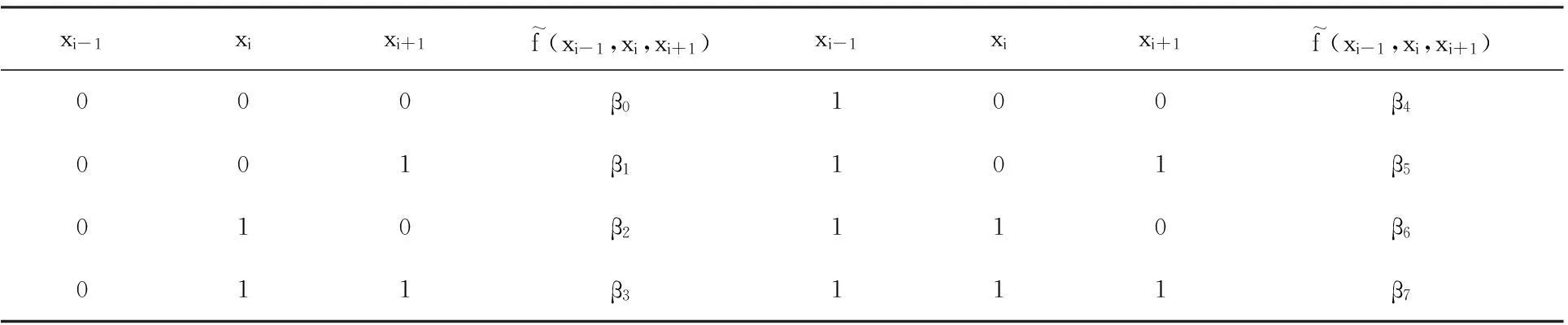
表1 初等细胞自动机的布尔函数真值表
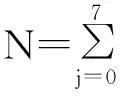
2Bernoulli移位规则的动力学
Chua等人借助于细胞自动机特征函数(characteristic function)、前向映射(forward map)以及树图(basin tree diagram),在有限长度的符号序列空间中完整刻画了256个初等细胞自动机的轨道渐近性质。文[26]在有限长度的符号序列空间中给出了细胞自动机的88个全局等价类。在任意选取初始条件的基础上,通过大量的计算机模拟以及对前向映射的分析,将88个等价类规则分为四类:(1)40类周期规则(周期1,周期2和周期3);(2)30类鲁棒性Bernoulli移位规则;(3)10类复杂Bernoulli移位规则;(4)8类超Bernoulli移位规则。对于初等细胞机的分类研究,最早始于C.C.Walker和W.R.Ashby(1966年)[49],接着是O.Martin,A.M.Odlyzko和Wolfram(1984年)[50,51],随后是W.Li和N.Packard(1990年)[37],A.Wuensche(1992年)[52]。文[53]在符号动力学框架下对256个初等细胞自动机的拓扑共扼分类(88类)给出了严格的证明(2007年)。当然,一些新的分类技术和方法仍然在不断涌现,比如文[54]运用了记忆分类的方法。这些分类,尤其是拓扑共轭分类,意味着只要考虑属于不同的全局等价类的规则所得细胞自动机的动力学行为即可。这将大大地节省人们在研究细胞自动机动力学行为的成本与时间。
Hedlund对一维细胞自动机作了严格的数学定义,把“与符号序列空间上的移位可交换的连续映射”称为细胞自动机,并且证明了这个定义与最初的以状态空间、邻域半径及局部规则这三者确定细胞自动机的定义一致。因此,用符号动力系统研究细胞自动机是一种必然的发展趋势。在Chua等人工作的启发下,尤其是利用特征函数和前向映射发现细胞自动机Bernoulli移位特性,近年来我们在双边无穷的条件下从符号动力学的角度详细地刻画了鲁棒性Bernoulli规则的动力学性质和混沌性状。由于在理论上已经证明关于细胞自动机的任何一个非平凡的命题都是不可判定的,因此我们必须针对不同类别的细胞自动机研究它们各自所特有的动力学行为。为清晰和方便起见,下文专门就规则10的符号动力学性质给出详细说明,展示了在符号动力学框架下研究初等细胞自动机动力行为的方法与技巧。
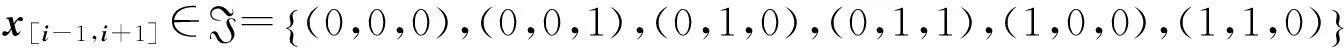
由于f10在Λ的动力学行为等价于有限性子位移Λ的动力学行为,所以下面我们通过有限性子位移的动力学性质来刻画f10在Λ的动力学性质。
由于正拓扑熵蕴涵着Li-Yorke意义下的混沌,而拓扑混合性蕴涵着多种意义下的混沌,如Devaney意义下的混沌和Li-Yorke意义下的混沌等等[47,48,55]。综上所述,有:
命题2.3f10在子系统Λ上既具有Li-Yorke意义下的混沌,又具有Devaney意义下的混沌。同时,f10在其全局吸引子上具有Li-Yorke意义下的混沌。
按照上述研究方案和技术路线,我们已经初步完成了如下三方面的研究:(1)刻画了30类鲁棒性Bernoulli移位规则的符号动力学性质,如拓扑混合性,拓扑熵,拓扑传递性等。(2)发现了在周期性规则中的非鲁棒性Bernoulli移位规则,并刻画了其混沌的符号动力学行为。如文[45,56]借助于细胞自动机特征函数与树图发现鲁棒性周期1规则40和鲁棒性周期2规则37都具有非鲁棒性Bernoulli移位特性,并进一步地从符号动力学角度证明了这些规则的复杂动力学行为。(3)讨论了部分复杂Bernoulli移位和超Bernoulli移位规则中的混沌子系统。这些结论揭示了Bernoulli移位,即滑翔机(glider)在刻画细胞自动机符号动力学性质中的作用。由此,首先文[57]给出了滑翔机的数学定义,随后文[46]借助于文[40]所定义的块映射(blocking transformation)和释放映射(releasing transformation)证明了“细胞自动机中的滑翔机意味着混沌”这个命题。这个结论回答了如下两个问题:(1)是否存在具备普适计算能力且拥有混沌动力学性质的细胞自动机[58];(2)能否从细胞自动机模拟演化图中推导出其混沌的符号动力学性质[59,60]。
值得注意的是,上述方法适用于非加性、非满的、非等度连续的、非正扩张以及非置换的细胞自动机。这深刻揭示了细胞自动机复杂的动力学性质,丰富了细胞自动机的符号动力学理论。在刻画细胞自动机符号动力学性质中,这些结论只是沧海一粟,还有待提出更多技巧与方法。
3结束语
刻画“由细胞自动机定义的动力系统的非线性动力学性质”是细胞自动机理论研究中的经典命题。具备一些特殊性质的细胞自动机的符号动力学行为已得到详细地结论(如满的、加性的、正扩张的、等度连续的等等)。满足这些性质的细胞自动机数目不多,仍然有大量全局映射(尤其是非加性的)的动力学行为还尚未知晓。本文中我们借助一维符号动力系统的思想和方法阐述了刻画Chua分类中Bernoulli移位规则在双边无穷的条件下的动力学性质与混沌性质的方法。这些规则大部分是非加性,非满的,非等度连续和非扩展的。从符号动力学角度看,这些Bernoulli移位规则拥有非常复杂的动力学行为,如正拓扑熵和拓扑混合性等。同时,这里阐述的方法也对刻画复杂Bernoulli移位规则和超Bernoulli移位规则的符号动力学行为有所帮助。
参考文献
[1]Neumann J. Theory of self-reproducing automata (Edited and completed by Burks A.W.)[M]. Champaign: University of Illinois Press,1966.
[2]Wolfram S. Theory and applications of cellular automata[M]. Singapore: World Scientific,1986.
[3]Jia B, Jiang R, Wu Q S. Traffic behavior near an off ramp in the cellular automaton traffic model[J]. Physical Review E,2004,69(5):056105.
[4]Prosperini N, Perugini D. Application of a cellular automata model to the study of soil particle size distributions[J]. Physical A,2007,383(2):595-602.
[5]Sieburg H B, McCutchanb J A, Claya O K, et al. Simulation of HIV infection in artificial immune systems[J]. Physical D,1990,45(1-3):208-227.
[6]Jiang R, Wu Q S. The adaptive cruise control vehicles in the cellular automata model[J]. Physical Letter A,2006,359:99-102.
[7]Hopcroft J, Ullman J. Introduction to automata theory, languages and computation[M]. Addison-Wesley, Reading, Mass,1979.
[8]Langton C G. Self-reproduction in cellular automata[J]. Physica D,1984,10(1-2):135-144.
[9]Langton C G. Computation at the edge of chaos: phase transitions and emergent computation[J]. Physica D,1990,42:12-37.
[10] Burks A W. Essays on cellular automata[M]. Champaign:University of Illinois press,1970.
[11]Gardner M. The fantastic combinations of John Conway’s new solitaire game ‘life’[J]. Scientific American,1970,223:120-123.
[12]Hedlund G A. Endomorphisms and automorphisms of the shift dynamical system[J]. Mathematical System Theory,1969,3(4):320-375.
[13]Ohi F. Chaotic properties of the elementary cellular automata rule 40 in Wolfram’s class[J]. Complex Systems,2007,17:295-308.
[14]Favati P, Lotti G, Margara L. Additive one-dimensional cellular automata are chaotic according to Devaney’s definition of chaos[J]. Theoretical Computer Science,1997174:157-170.
[15]Cattaneo G, Finellt M, Margara L. Investigating topological chaos by elementary cellular automata dynamics[J]. Theoretical Computer Science,2000,244:219-241.
[16]Hurd L P, Kari J, Culi K. The topological entropy of cellular automata is uncomputable[J]. Ergodic Theory and Dynamic Systems,1992,82(255):255-265.
[17]Damico M, Manzini G, Margara L. On computing the entropy of cellular automata[J]. Theoretical Computer Science,2003,290:1 629-1 646.
[18]Juarez Martinez G, McIntosh H V, Seck TuohMora J C. Production of gliders by collisions in rule 110[J]. Lecture Notes in Computer Science,2003,2801:175-182.
[19]Wolfram S. Statistical mechanics of cellular automata[J]. Review Modern Physics,1983,55(3):601-644.
[20]Wolfram S. Universality and complexity in cellular automata[J]. Physica D,1984,10(1):1-35.
[21]Akin H. The topological entropy of nth iteration of an additive cellular automata[J]. Applied Mathematics and Computation,2006,174:1 427-1 437.
[22]Allouche J P, Skordev G. Remarks on permutive cellular automata[J]. Journal of Computer and System Sciences,2007,67:174-182.
[23]Wolfram S. A new kind of science[M]. Wolfram Media, Inc., Champaign, Illinois,2002.
[24]Chua L O, Yoon S, Dogaru R. A nonlinear dynamics perspective of Wolfram’s new kind of science, part I: threshold of complexity[J]. International Journal of Bifurcation and Chaos,2002,12(12):2 655-2 766.
[25]Chua L O, Sbitnev V I, Yoon S. A nonlinear dynamics perspective of Wolfram’s new kind of science, part II: universal neuron[J]. International Journal of Bifurcation and Chaos,13(9):2 377-2 491.
[26]Chua L O, Sbitnev V I, Yoon S. A nonlinear dynamics perspective of Wolfram’s new kind of science, part III: predicting the unpredictable[J]. International Journal of Bifurcation and Chaos,2004,14(11):3 689-3 820.
[27]Chua L O, Sbitnev V I, Yoon S. A nonlinear dynamics perspective of Wolfram’s new kind of science, part IV: from Bernoulli shift to 1/f spectrum[J]. International Journal of Bifurcation and Chaos,2005,15(4):1 045-1 183.
[28]Chua L O, Sbitnev V I, Yoon S. A nonlinear dynamics perspective of Wolfram’s new kind of science, part V: fractal every where[J]. International Journal of Bifurcation and Chaos,2005,15 (12):3 701-3 849.
[29]Chua L O, Sbitnev V I, Yoon S. A nonlinear dynamics perspective of Wolfram’s new kind of science, part VI: from time-reversible attractors to the arrows of time[J]. International Journal of Bifurcation and Chaos,2006,16(5):1 097-1 373.
[30]Chua L O, Guan J B, Valery I S, et al. A nonlinear dynamics perspective of Wolfram’s new kind of science, part VII: isle of Eden[J]. International Journal of Bifurcation and Chaos,2007,17(9):2 839-3 012.
[31]Chua L O, Karacs K, Sbitnev V I, et al. A nonlinear dynamics perspective of Wolfram’s new kind of science, part VIII: more isles of Eden[J]. International Journal of Bifurcation and Chaos,2007,17(11):3 741-3 894.
[32]Chua L O, Pazienza G E, Orzo L, et al. A nonlinear dynamics perspective of Wolfram’s new kind of science, part IX: quasi-ergodicity[J]. International Journal of Bifurcation and Chaos,2008,18(9):2 487-2 642.
[33]Chua L O, Pazienza G E, Shin J. A nonlinear dynamics perspective of Wolfram’s new kind of science, part X: period-1 rules[J]. International Journal of Bifurcation and Chaos,2009,19 (5):1 425-1 654.
[34]Chua L O, Pazienza G E, Shin J. A nonlinear dynamics perspective of Wolfram’s new kind of science, part XI: period-2 rules[J]. International Journal of Bifurcation and Chaos,2009,19(6):1 751-1 930.
[35]Chua L O, Pazienza G E. A nonlinear dynamics perspective of Wolfram’s new kind of science, part XII: period-3 rules, period-6 rules, and permutive rules[J]. International Journal of Bifurcation and Chaos,2009,19(12):3 887-4 038.
[36]Chua L O, Pazienza G E. A nonlinear dynamics perspective of Wolfram’s new kind of science, part XIII: Bernoulli shift rules[J]. International Journal of Bifurcation and Chaos,2010,20(7):1 859-2 003.
[37]Li W, Packard N. The structure of the elementary cellular automata rule space[J]. Complex Systems,1990,4(3):281-297.
[38]Hurd L P, Kari J, Culi K. The topological entropy of cellular automata is uncomputable[J]. Ergodic Theory and Dynamic Systems,1992,82(255):255-265.
[39]Chen F Y, Jin W F, Chen G, et al. Chaos of elementary cellular automata rule 42 of Wolfram’s class II[J]. Chaos,2009,19:013 140.
[40]Jin W F, Chen F Y. Topological chaos of universal elementary cellular automata rule[J]. Nonlinear Dynamics,2011,63:217-222.
[41]Jin W F, Chen F Y, Chen G, et al. Complex symbolic dynamics of Chua’s period-2 rule 37[J]. Journal of Cellular Automata,2010,5 (4-5):315-331.
[42]Jin W F, Chen F Y, Chen G, et al. Extending the symbolic dynamics of Chua’s Bernoulli-shift rule 56[J]. Journal of Cellular Automata,2010,5(1-2):121-138.
[43]Chen F F, Chen F Y. Complex dynamics of cellular automata rule 119[J]. Physica A,2009,388:984-990.
[44]Chen F F, Chen F Y, Chen G R, et al. Symbolic dynamics of elementary cellular automata rule 88[J]. Nonlinear Dynamics,2009,58:431-442.
[45]Chen L, Chen F Y, Jin W F, et al. Some non-robust Bernoulli-shift rules[J]. International Journal of Bifurcation and Chaos,2009,19(10):3 407-3 415.
[46]Jin W F, Chen F Y, Chen G R. Glider implies Li-Yorke chaos for one-dimensional cellular automata[J]. Journal of Cellular Automata. (In Press)
[47]周作领.符号动力系统[M].上海:上海科技教育出版社,1997.
[48]Kitchens B. Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts[M]. Berlin: Springer Verlag,1998.
[49]Walker C C, Ashby W R. On temporal characteristics of behavior in certain complex systems[J]. Kybernetik,1966,3(2):100-108.
[50]Martin O, Odlyzko A M, Wolfram S. Algebraic properties of cellular automata[J]. Communications in Mathematical Physics,1984,93(2):219-258.
[51]Wolfram S. Cellular automata as models of complexity[J]. Nature,1984,311(4):419-424.
[52]Wuensche A, Lesser M. The Global Dynamics of Cellular Automata[M]. Santa Fe Institute Studies in the Sciences of Complexity, Addison-Wesley Publishing Company,1992.
[53]Guan J B, Shen S W, Tang C B, et al. Extending Chua’s global equivalence theorem on Wolfram’s new kind of science[J]. International Journal of Bifurcation and Chaos,2007,17(2):4 245-4 259.
[54]Genaro J M. A note on elementary cellular automata classication[J]. Journal of Cellular Automata,2013,8(34):233-259.
[55]Blanchard F, Glasner E, Kolyada S, et al. On Li-Yorke pairs[J]. Journal Reine Angewandte Mathematik,2002,547:51-68.
[56]Jin W F, Chen F Y, Chen G R, et al. Complex symbolic dynamics of Chua’s period-2 of rule 37[J]. Journal of Cellular Automata,2010,5(4-5):315-331.
[57]Chen F Y, Shi L, Chen G R, et al. Chaos and gliders in periodic cellular automata rule 62[J]. Journal of Cellular Automata,2012,7:287-302.
[58]Delvenne J C, Kurka P, Blondel V. Decidability and universality in symbolic dynamical systems[J]. Lecture Notes in Computer Science,2005,3 354:104-115.
[59]Kosaraju S R. On some open problems in the theory of cellular automata[J]. IEEE Transactions on Computers,1974,23(6):561-565.
[60]Boyle M. Open problems in symbolic dynamics[J]. Contemporary mathematics,2008,469:69-118.
[61]金伟锋.二维符号动力学与细胞自动机[D].金华:浙江师范大学,2009.
[62]陈琳.若干一维细胞自动机动力学行为的复杂性研究[D].金华:浙江师范大学,2009.
[63]陈方方.Bernoulli移位细胞自动机的符号动力学研究[D].金华:浙江师范大学,2009.
[64]韩云芳.一类超Bernoulli移位细胞自动机的动力学研究[D].杭州:杭州电子科技大学,2010.
[65]管俊彪.细胞自动机和符号动力系统[D].金华:浙江师范大学,2006.
Simple Rules, Complex Behaviors—Symbolic Dynamics of
Elementary Cellular Automata
Chen Fangyue1, Jin Weifeng2
(1.DepartmentofMathematics,SchoolofScience,HangzhouDianziUniversity,Hangzhou,Zhejiang, 310018,China;
2.DepartmentofMathematics,SchoolofScience,ShanghaiUniversity,Shanghai, 200444,China)
Key words: elementary cellular automata; rule; symbolic dynamics; chaos; topologically mixing; topological entropy
