双螺杆压缩机端盖加工工艺规程规划的蚁群算法研究*

章正伟

(浙江交通职业技术学院 机电与航空学院，杭州　311112)



双螺杆压缩机端盖加工工艺规程规划的蚁群算法研究*

章正伟

(浙江交通职业技术学院 机电与航空学院，杭州311112)

摘要：双螺杆压缩机以其优良的运行平稳性在矿用工业中被推广应用，为满足产能要求，在研究其端盖加工工艺基础上，采用蚁群算法研究双螺杆压缩机端盖加工工艺规程规划方案。研究了实际加工情况，引入工艺约束关系矩阵并提出“或”型工艺约束，针对此复杂问题编制了加工要素选择模块，并采用启发式要素选择规则，改进了蚁群算法的结构。在充分研究端盖-腔体装配过程后，锁定了端盖的关键加工要素。在此基础上编制了零件的工艺约束模型，代入算法求解，实现了加工工艺规程规划的自动化，并通过与人为经验工艺设计进行对比，说明了此算法的有效性并具有更高的经济性。

关键词：单边装配线；U型装配线；粒子群算法；优化

0引言

双螺杆压缩机在机械工业中被推广应用，具有较大的市场需求，故面对市场需求的增加，需对产品加工工艺规程合理编排，在保证产品工艺稳定性基础上提升产品产量。此问题属于机械加工过程中的加工工艺规程规划问题。加工工艺规程规划问题直接影响零件的加工成本，并影响零件的工艺稳定性。目前针对加工工艺规程规划问题中合理的加工工艺序列的编制问题，已有较多人进行研究：文献[1]通过引进了工艺约束矩阵从而实现对加工序列的合法性识别，综合考虑了降低装夹次数与工序转换次数，并通过采用遗传算法求解此问题，得到实用结果；文献[2]则通过建立工艺要素之间的质量相关性并以此建立一个机床-夹具-刀具-加工方式之间的工艺系统，通过分析所有可能影响工艺质量的分要素并研究不同质量要素之间的约束关系从而分析出改进零件工艺质量所需的投入成本；文献[3-4]分别采用与车间资源匹配最优和加工工序之间关联性较优的方法进行工艺加工路线的选择，取得了一定效果；文献[5]则对加工过程中刀具的空行程路径进行了规划，采用启发式-遗传混合算法求解取得较好效果；文献[6]则通过对叶片加工过程中的整个机床系统建立数学约束条件，对叶片各工序加工时间进行优化从而降低了整体加工成本；文献[7-9]采用遗传算法对加工工步的排序问题进行研究，从而降低整体加工时间或降低辅助加工时间。但以上研究均未考虑到当前实际生产中将工序集合归并为工位的工艺组织方式，并未考虑工位之间的加工效率平滑因素(平滑因素即工位之间加工时间的平衡性)对实际产量的影响，而当前加工制造业利润空间增长有限，研究高效率的加工工艺规程规划方案成为紧迫问题。故本文的研究重点在于为零件所有加工元素所对应的工序进行归属工位的划分，在工序划分时，需以加工工步间先后关系为约束条件，以产生逻辑合理、工位间平衡率较高的工位划分方案为目标。此问题与装配线平衡问题有相似的优化目标，但需考虑零件的加工工艺约束，称此问题为工艺优化平衡问题(Process Balance Optimization Problem, PBOP)。最后，对某型双螺杆压缩机的端盖零件作为应用实例，并分析其工艺编排经济性。

1工艺优化平衡问题工艺约束的实现

文献[1]将一个被加工特征细分为多个加工内容，如将铣面划分为：粗铣、半精铣、精铣、磨削(如有较高平面度和粗糙度要求时)，再将拆分出的细小不可分加工内容进行再次组合优化。而在实际生产过程中，针对同一被加工要素，粗/精加工往往合并连续加工而不分离，因为针对同一加工要素的加工内容需要连续操作，方能降低机床定位轴的往复运动从而提高加工精度(如对于同一定位销孔，可以将初钻孔，铰孔工序紧凑安排，防止由于粗精加工分离引起机床重复定位误差导致销孔位置度尺寸的过程控制能力不足)，节约空行时间。针对本文求解零件模型的复杂性，包含多种类型的被加工要素，如铣面、钻孔/攻丝组合、钻孔/铰孔组合、钻孔/镗孔组合、深长孔工步组合等，若将所有要素的加工内容均根据加工工步进行拆分计算，将大大增加问题的计算规模，故限制最小不可分任务为被加和工要素(即将加工要素的粗加工工步和精加工工步合并为一个不可拆分的整体)。

明确被优化的最小任务为被加工要素之后，若要检验产生的工位划分序列是否符合被加工要素之间的逻辑关系(即先后加工次序关系)，则需定义约束矩阵，本文借鉴了文献[1]的约束矩阵定义方式，即：

若要素i优于要素j进行加工，则cij=1；否则说明i与j之间无约束关系，cij=0。但文献[1]并未考虑实际加工条件中“或”型加工约束条件的存在，即存在要素k，既可在要素i完成后立即被加工，也可在要素j完成后立即被加工；且当i被加工后，要素k可被加工并忽视其紧前要素j是否被加工。称以上约束关系为“或”型约束，即k的紧前要素i和j中，只需有任意一项完成加工，k便能进行加工。对此类约束，设cik=cjk=2。在“或”型约束条件下，若i已被加工，则i与k的紧前关系释放，则cik的值由2变为-1，表示i对k的约束已经结束。综上，cij的可能取值为：

cij=(-1,0,1,2)

(1)

在公式(1)中，若cij为-1则表示任务i对任务j的“或”型约束已经释放；若cij为0则表示任务i与任务j之间并不存在工艺约束关系；若cij为1则表示任务i为任务j的紧前工序，任务j开启的必要前提为任务i已加工完毕；若cij为2则表示任务i与任务j之间存在“或”型约束关系。相比于文献[1]，增加“或”型约束的意义在于，某被加工要素k，能由i要素作为定位基准的条件下被加工，也能由j要素作为定位基准的条件下被加工，具有以下优点：①使得加工工艺规程规划中，要素k的加工定位与夹持方式直接体现于工艺约束矩阵中，从而更贴近实际加工工艺情况，②同时也使得工序链的可能构成种类更多，即增加了工序组合的多样性。

1.1加工工艺规程规划及数学模型

如图1所示，在零件生产线中，整条生产线划分为6个工位，每个工位包含不同的加工要素内容组合，被加工零件在一个工位中一次装夹，完成本工位加工内容后转移到下一工位。图2所示为加工工艺约束图例，t表示要素加工时间，4→8和7→8为虚约束，表示若要素4已被加工，则要素8可被加工且忽视要素7对8的约束。工位内部的加工要素编排以及工位之间加工要素先后顺序编排均符合工艺约束矩阵。若将图2所包含的加工要素按图2约束放入图1的加工生产线中，图3为一种可能的工艺序列编排方案。在图3中，由于要素4早在工位3便完成加工，故与其符合虚约束关系的要素8可提前至工位4加工，此时已经释放要素7对要素8的约束作用。而若未引入虚约束的概念，则要素8必须在要素4和7均完成后方可加工，无疑减少了工艺编排的更多可能性和灵活性。

图1　加工生产线示例

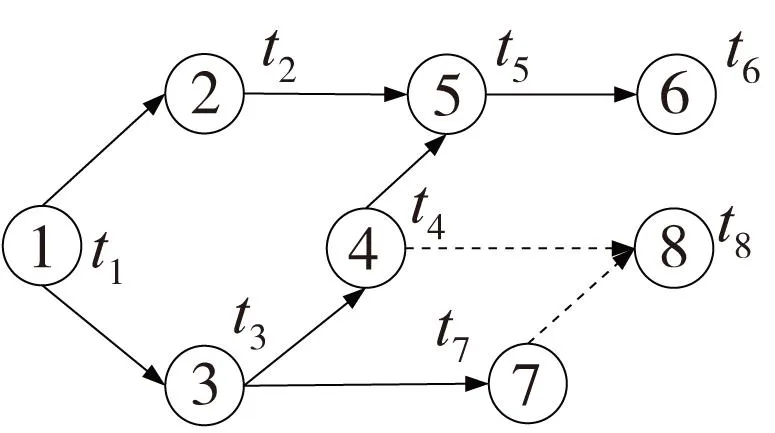
图2　加工工艺约束图例

图3一种满足图2的6工位工艺编排方案

在满足约束矩阵的前提下，同时加工要素的编排要以平衡化整条生产线为目标，使得各个工位的加工时间趋于一致而消除瓶颈，即在节拍约束确定条件下使得生产线机床利用率最高，称此问题为工艺优化平衡问题(Process Balance Optimization Problem, PBOP)。而本文的研究目的在于将装配线平衡理论引入工艺优化平衡领域，考虑工艺优化问题特殊特点的基础上采用高效的装配线优化平衡方法，提高加工工艺规程规划的平衡率。

故机械加工生产线的工艺平衡规划问题数学模型类似于单边装配线平衡问题[10-11]，但相关字母的含义已根据加工工艺规程规划问题而变化：

s.t． Mx∩My= Фx≠yx、y = 1,2,…,m

(2)

(3)

(4)

∀i∈Sxj∈Sy若 cij= 1或2 则 x ≤ y

(5)

式中:Mx、My分别表示工位x和工位y；Ф为空集; 第k个工作站所包含加工要素集合为Mk，即Mk={ i | 任务 i 划分归属于工位k } ;E为生产线上所有加工要素的集合，E={ 1,2,…,n} ; n为要素总数;要素间工艺约束为cij，若要素i与j直接相连，要素i先于j则cij=1或等于2，否则cij= 0; m为工位总数; Tk为第k个工位的加工时间之和。数学模型中的公式含义如下。式(2)表示体现加工要素分配的唯一性，即单一加工要素只能在某一个工位中进行加工，此假设说明单一加工要素不能被拆分，也不能同时在不同工位中出现;式(3)确保所有加工要素都被分配，即表示零件的所有加工要素均要排布于所有工位中，不能出现遗漏加工要素的情况;式(4)表示每个工位的要素加工时间总和均小于预设节拍时间C，即表示每个工位的要素加工时间累计需满足小于节拍时间的约束条件；式(5)表示要素分配过程的先后约束关系。

2工艺平衡优化问题的蚁群算法

蚁群算法的整体算法流程如图4所示，从图4中可知，解的构造为最关键模块。本文的蚁群算法借鉴了文献[12]，但由于所求解的问题已发生改变，需针对加工工艺规程规划的问题特征对原算法解构造模块进行改进。分析图5所示解的构造算法流程，对于所解决的加工工艺规程规划的问题，关键在于根据工艺约束矩阵以及数学模型的规则筛选出可被选择的加工要素集合DS。故在算法的具体介绍中，围绕蚁群算法引入加工工艺规程规划问题的适应性改进而展开。

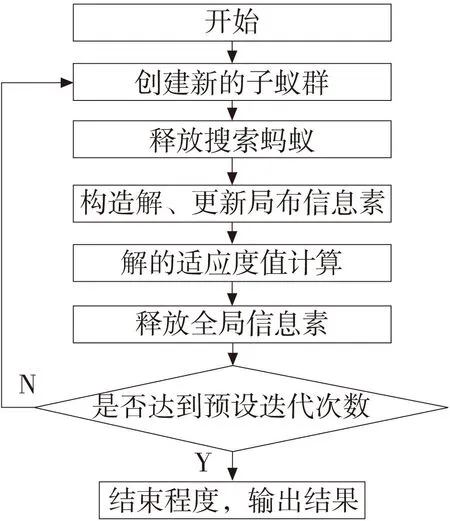
图4　蚁群算法流程

2.1蚁群算法解的构建

解的构建模块：如图5所示解的构建过程中，每只蚂蚁当前工位下进行加工要素的选择时，需首先生成可供直接分配的加工要素集合DS，再从中采用蚁群综合信息搜索规则选择加工要素。解的构建主要由两个分模块组成，分别为：可供直接分配的要素集合(DS)生成模块、蚁群综合信息要素搜索规则模块。

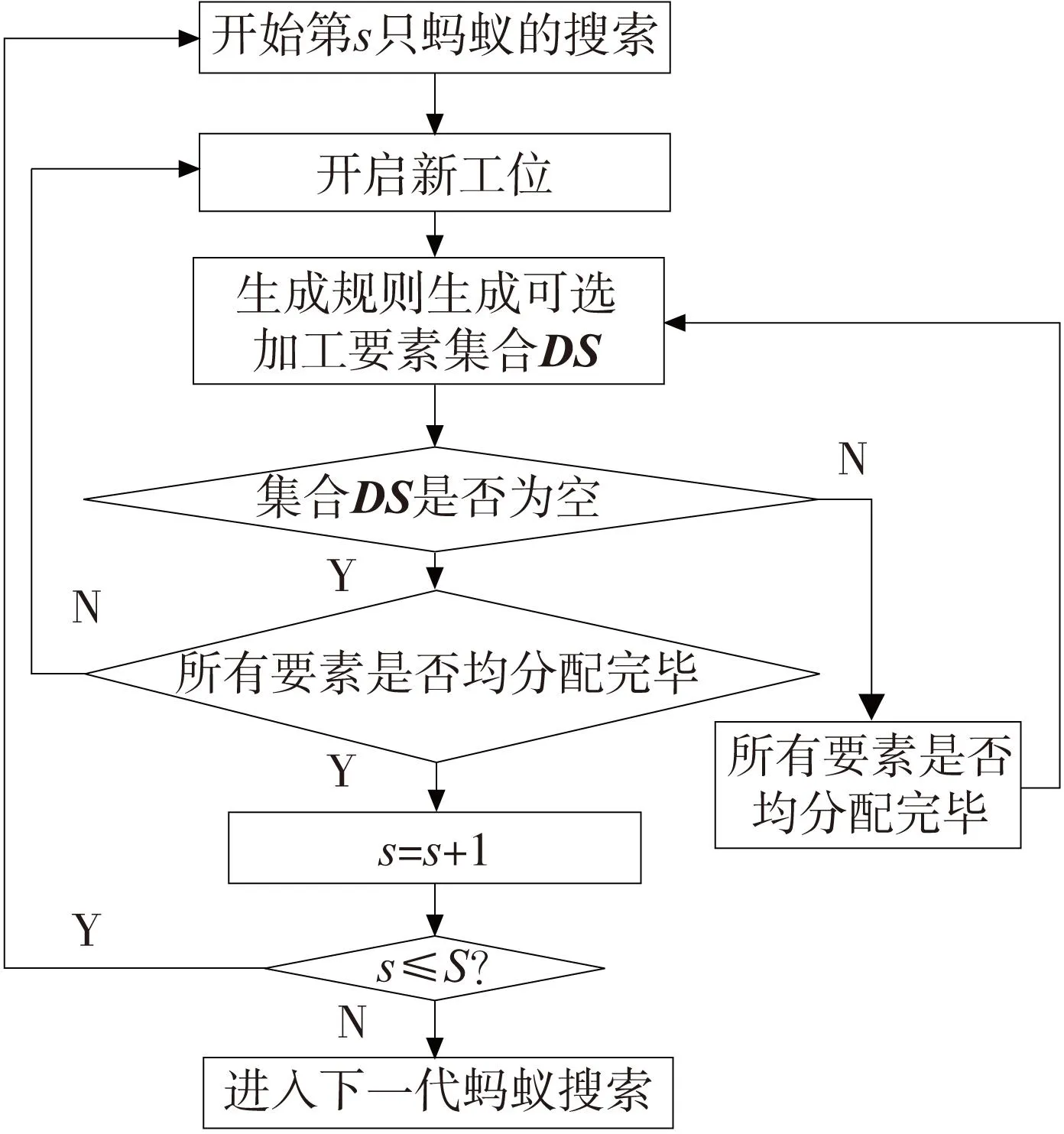
图5　解的构造算法流程

DS生成模块：为解决本文所引入的“或”型约束，并考虑工艺约束矩阵的限制条件，可选要素筛选过程算法构建如下：

(1)首先根据工艺约束矩阵，查找当前紧前要素均已被安排完毕的加工要素，生成初始可被分配加工要素集合IS。对此，由于“或”型约束条件的存在，针对被判断要素j，有多种情况：

①若∃i∈E，cij=1成立，则说明要素j还有未被分配的紧前要素，故要素j不能被选取入IS集合；

②若∀i∈E，cij≠1均成立，且∀i∈E使得cij=-1成立，则说明要素j的所有紧前要素均已被分配，要素j已经自由并可放入IS；

③若∀ i∈E，cij≠1均成立，且∀i∈E，cij≠-1和cij≠-2均成立，说明要素j不存在任何紧前要素或虚约束，要素j可放入IS；

④若∀i∈E，cij≠1均成立，∃i∈E， 使得cij=2成立，则说明要素j至少存在两个以上的虚约束紧前要素未被分配，且未有任意一个虚约束被解除，故任务j不能被放入IS。

(2)在(1)基础上，进一步判断IS中加工要素，是否满足约束公式(4)，剔除不满足此公式的加工要素，形成可直接供分配的加工要素集合DS，同时，当从DS集合中选择出某一加工要素后，需释放与该加工要素有关的所有虚约束；

蚁群综合信息要素搜索规则：蚁群综合信息搜索规则算法[9]采用加工要素加工时间信息为启发式信息，构造如下混合搜索机制，综合了随机搜索、信息要素-启发式信息搜索两种搜索机制：

(6)

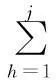
3矿用双螺杆压缩机端盖制造工艺

3.1装配要求对加工工艺影响分析

如图6所示为矿用双螺杆压缩机的腔体和左/右端盖装配爆炸图。图6中定位销所在的右侧端盖为加工制造的难点部件，图7为右侧端盖的三视图，在图7所标示此部件的关键加工要素为B面两镗孔以及A面两销孔，其中，两镗孔用于安装双螺杆，故双螺杆相对于腔体的定位准确度取决于右侧端盖安装轴承的镗孔相对于定位销孔(均见图7标示)的位置度加工精度。若两端盖镗孔的位置精度不高，导致图6中位于左/右端盖与中间腔体装配后，两端盖左/右相对镗孔的同心度尺寸超差，从而使双螺杆装配过程中存在变形，导致装配应力的增加。而此装配应力也会直接影响轴承的径向应力，从而也影响轴承寿命。

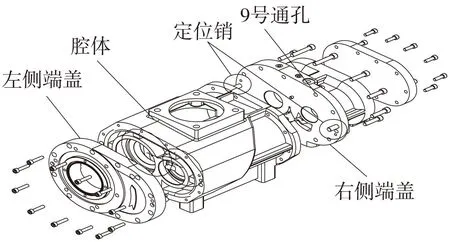
图6　矿用双螺杆压缩机客体装配爆炸图

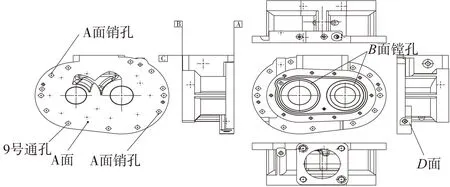
图7　矿用双螺杆压缩机端盖三视图

由于此要求，使得端盖加工过程中，镗孔的位置度尺寸为必须保证的关键尺寸加工要素。为保证镗孔相对于定位销孔的位置精度，将两种加工要素安排于同一工位加工(则加工精度近似于机床本身定位精度，为最合理的工艺安排)。且由于销孔位于A基准面上，而镗孔尺寸(为图7主视图所示的两个较大中心内孔)位于B基准面上，而A面与B面位于端盖的两侧(见图7)，加工方向相反，为保证销孔能与镗孔一同加工，故使A基准面的加工优先级更高，从而使得销孔与B面镗孔共序加工时，A面已加工完毕，不会出现先加工销孔而再铣A面的不合理工艺。

3.2端盖加工要素工艺分析

图7为端盖的三视图，共有被加工要素59个，按照加工要素在加工面上的分布，将加工要素归结到A面、B面和C面、D面(D面为孔的台阶面，面积较小且加工时间短)上，其中C面为法兰面、D面虚拟为端盖的所有侧面集合(将端盖所有侧面归集到与D面一道加工是基于目前加工中广泛使用的第四轴设备，可以采用一次定位加工360°侧面，从图7中可观察到端盖侧面存在不同角度的孔，且所有孔的轴线均与A/B面平行)。根据加工要素的加工方位，编制加工约束关系图：将位于A、B、C、D面的各加工要素归结为本加工面的紧后要素，则A、B、C、D面后跟随了位于本加工面的所有要素(见图8，分别为加工要素1、2、7、15，其中由于D面为某台阶孔的台阶面)；同时其中59为去毛刺工序，为所有加工尺寸的紧后要素，为简化加工约束关系图，未在图8中显示。为使在B面也能加工A面上的光孔且防止刀具过短而与零件干涉，采用了加长刀杆，则位于A面上位于端盖边缘的一圈孔和螺纹孔均也能与加工B面时一道加工，同时设置A面上外圈光孔等元素与A/B基准为“或”约束关系，在图8中采用虚线表示；例如图6和图7所示9号通孔位于A面上，若安排在加工B面时加工，为防止刀柄与B面下方四周毛坯面干涉，则须采用加长刀杆。加工要素的加工时间信息表见表1。

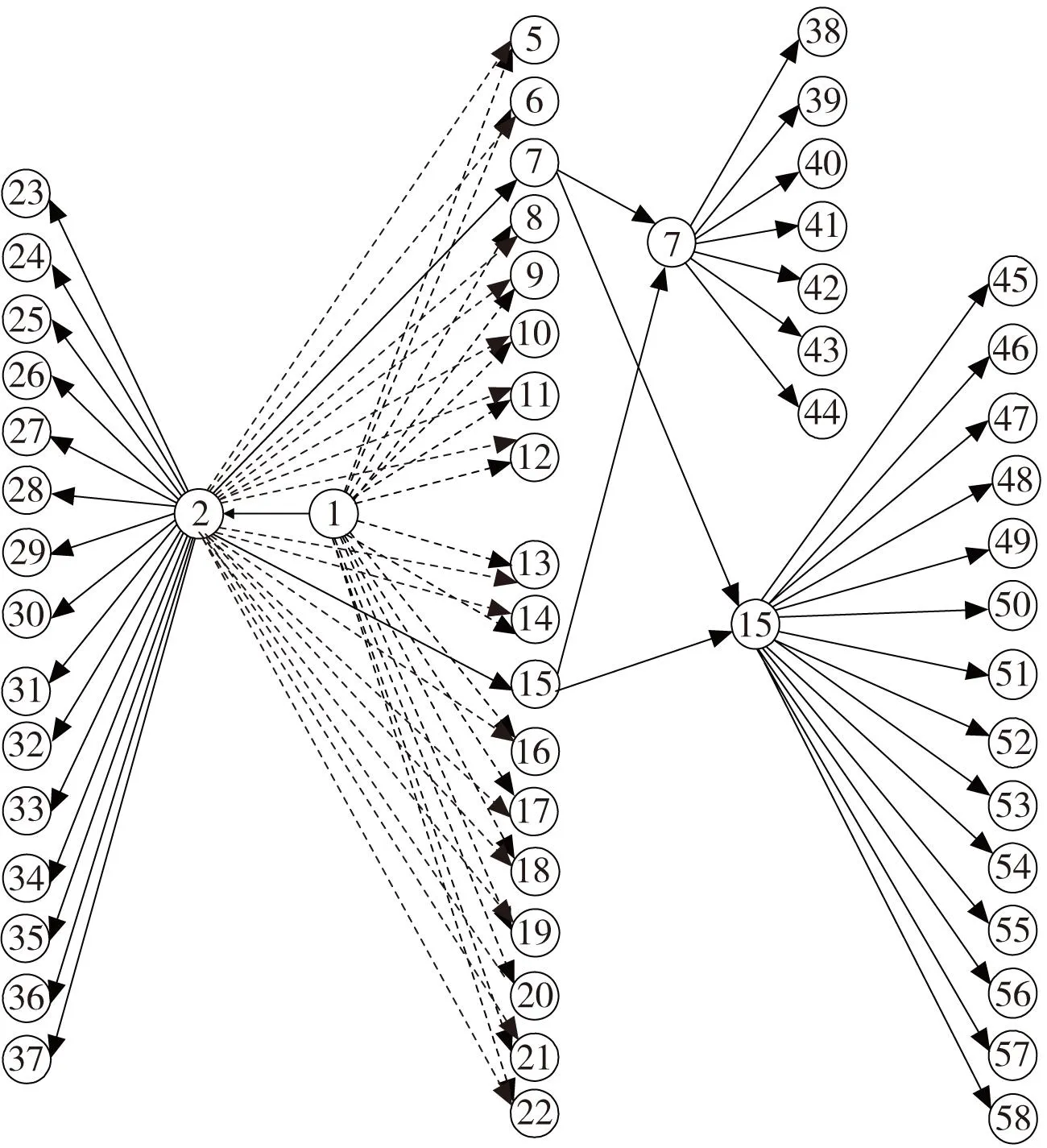
图8　加工约束关系图

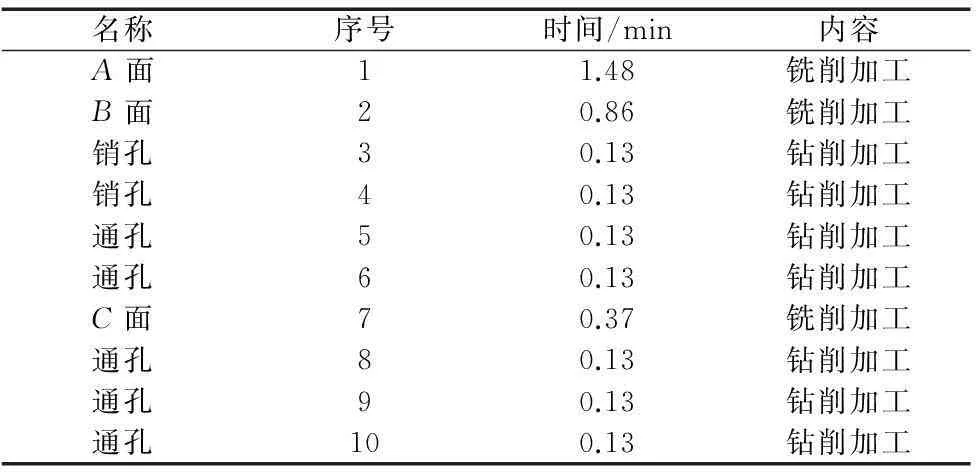
名称序号时间/min内容A面11.48铣削加工B面20.86铣削加工销孔30.13钻削加工销孔40.13钻削加工通孔50.13钻削加工通孔60.13钻削加工C面70.37铣削加工通孔80.13钻削加工通孔90.13钻削加工通孔100.13钻削加工

续表

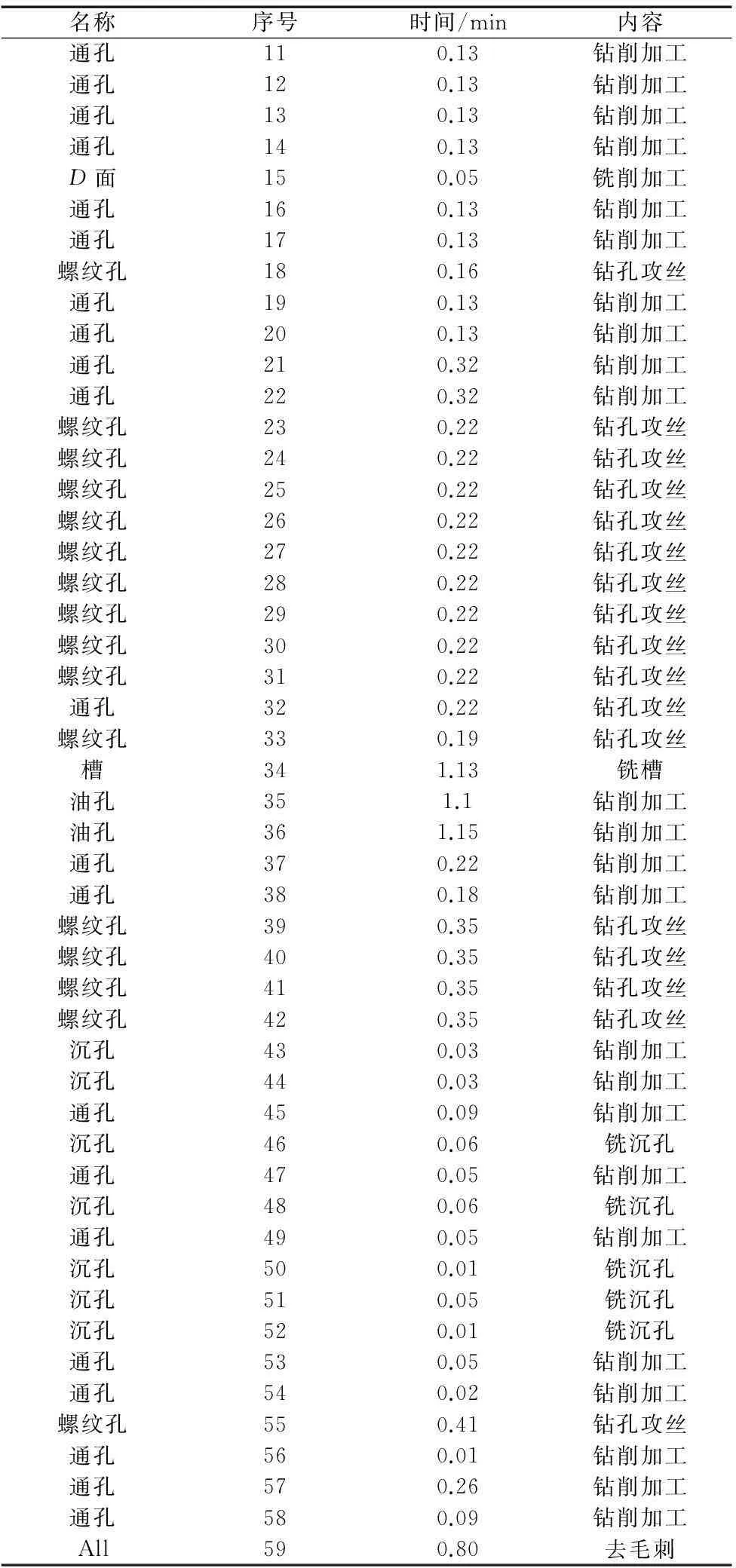
名称序号时间/min内容通孔110.13钻削加工通孔120.13钻削加工通孔130.13钻削加工通孔140.13钻削加工D面150.05铣削加工通孔160.13钻削加工通孔170.13钻削加工螺纹孔180.16钻孔攻丝通孔190.13钻削加工通孔200.13钻削加工通孔210.32钻削加工通孔220.32钻削加工螺纹孔230.22钻孔攻丝螺纹孔240.22钻孔攻丝螺纹孔250.22钻孔攻丝螺纹孔260.22钻孔攻丝螺纹孔270.22钻孔攻丝螺纹孔280.22钻孔攻丝螺纹孔290.22钻孔攻丝螺纹孔300.22钻孔攻丝螺纹孔310.22钻孔攻丝通孔320.22钻孔攻丝螺纹孔330.19钻孔攻丝槽341.13铣槽油孔351.1钻削加工油孔361.15钻削加工通孔370.22钻削加工通孔380.18钻削加工螺纹孔390.35钻孔攻丝螺纹孔400.35钻孔攻丝螺纹孔410.35钻孔攻丝螺纹孔420.35钻孔攻丝沉孔430.03钻削加工沉孔440.03钻削加工通孔450.09钻削加工沉孔460.06铣沉孔通孔470.05钻削加工沉孔480.06铣沉孔通孔490.05钻削加工沉孔500.01铣沉孔沉孔510.05铣沉孔沉孔520.01铣沉孔通孔530.05钻削加工通孔540.02钻削加工螺纹孔550.41钻孔攻丝通孔560.01钻削加工通孔570.26钻削加工通孔580.09钻削加工All590.80去毛刺

4 端盖加工生产线规划设计

根据预定年产量6～7.5万的目标，按每年工作周50计，预定每周产能为1200～1500套，因此每班产能为100～120套。故节拍时间(CT: Circle Time)预定为4～5min，针对PBOP问题，将预定节拍时间细化为以0.1min为级差的等差数列，采用蚁群算法进行运算，设置蚂蚁数目10，运算代数10。计算结果见表2，m为计算得到的工位数目(单位：个)，LB为平衡率(单位：%)。从求解效果看，可优选方案2，平衡率为92.4 %(参见表3中分配结果，平衡率的计算为将所有工位累计加工时间累加，再除以节拍时间与工位数的乘积，即LB=工位累计时间之和÷(节拍时间×工位数目))。表3为蚁群算法得出的PBOP问题按方案2分配结果，表3中，括号内数字表示任务的开始和结束时间(单位min)，如安排在工位1的最后一个被加工要素11(3.71, 3.84)表示加工要素11的开始加工时间为3.71min，加工结束时间为3.84min，各工位累计加工时间见表3末列累计值。

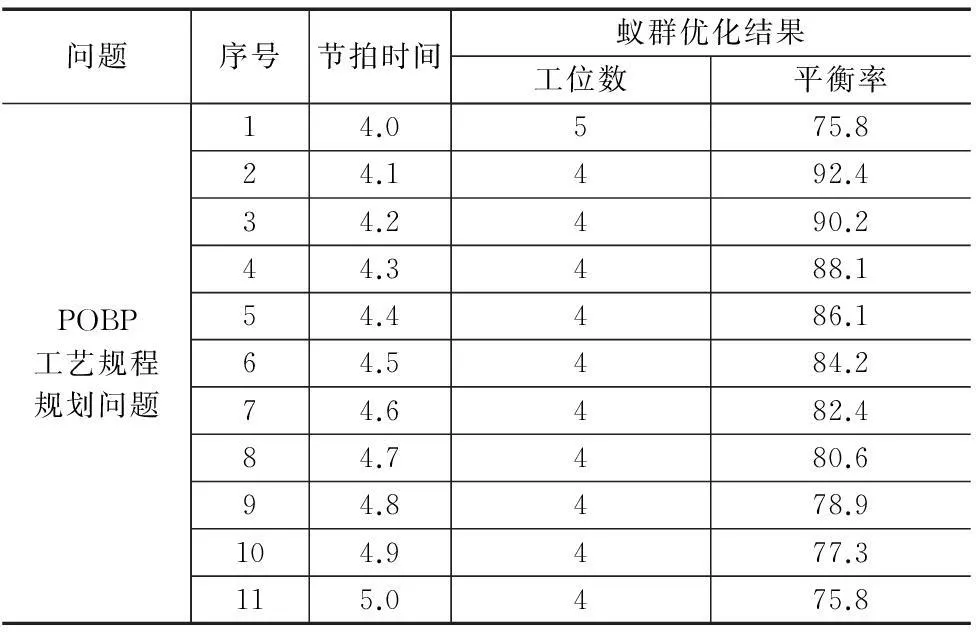
表2　各测试问题结果对比

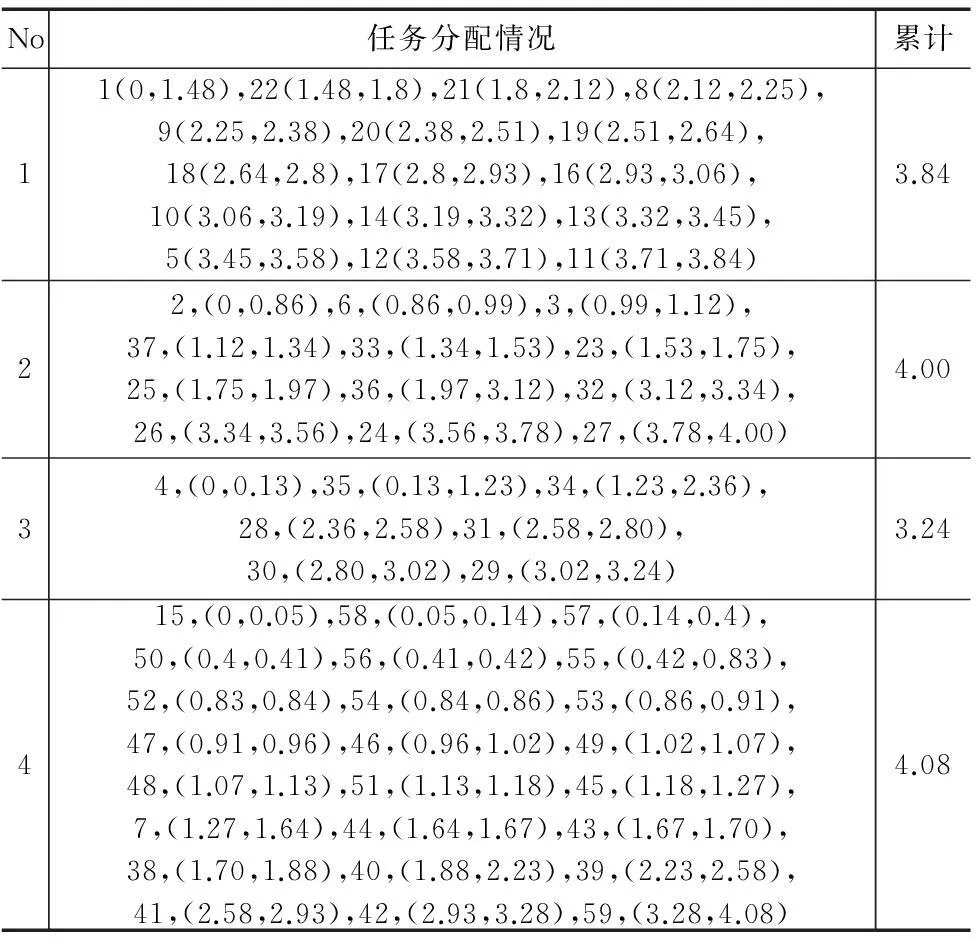
表3　蚁群算法方案2优化结果

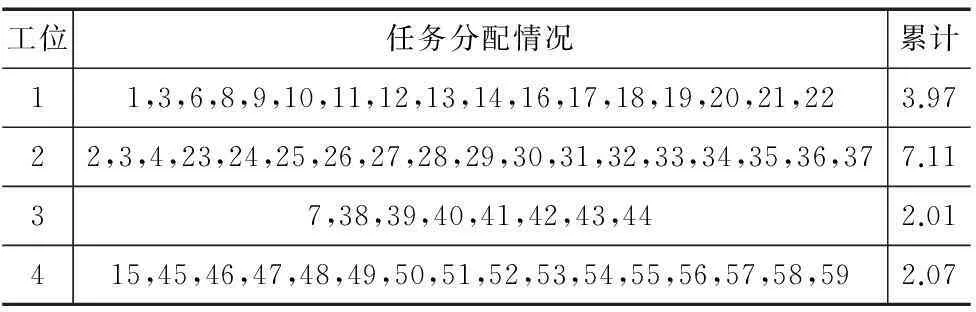
表4　人工经验方案

表4为人工经验排产的方案，累计列表示此工位的加工时间累计值。若按此方案排产，工序2的加工时间最长，故工序2为瓶颈工序，且生产线的平衡率仅为53.3%。由于工序2加工时间过长，导致工序1、工序3、工序4的累计时间与工序2累计时间相减后分别存在3.14min、5.1min、5.04min的时间差值，会带来以下影响：由于工序1相对于工序2生产过快，则在工序1和2之间会产生大量半成品；而在工序2和工序3之间，同样由于工序2过慢，导致工序3经常等待工序2的完工产品，对生产资源的利用明显不足。而采用本文蚁群算法之后，按表3所得方案生产线平衡率有39.1%的提高，成效明显。

5结束语

本文针对机械加工规划中的工位平衡问题(PBOP)进行了研究，引入了实际工艺问题中广泛存在的“或”型约束，使得工艺约束矩阵更符合实际加工情况。构造了一种蚁群算法，针对“或”型约束，建立了可选加工要素筛选模块，并在蚁群综合信息要素选择中分别采用两种启发式信息规则进行加工要素的选择。针对某型矿用螺杆压缩机的装备过程进行了分析，研究了其装配过程对端盖加工要素的影响，从而建立了合理的工艺约束矩阵。在此基础上将此实际案例代入算法求解，并与人工经验排产进行对比，生产制造线有39.1%的效率提升，验证了本文算法性能。

[参考文献]

[1] 胡于进,张正义,凌玲,等.基于工艺约束矩阵的加工序列优化[J].中国机械工程,2009,20(9):1062 -1066.

[2] 郑联语,唐晓青,汪叔淳.基于QFD的数控加工工艺质量优化规划方法[J].机械工程学报,2001,37(8): 38-42.

[3] 涂俊翔. 与车间资源匹配最优的工艺规划选择[J]. 组合机床与自动化加工技术,2013(4):125-128.

[4] 祝天荣,徐新胜,陶西柱. 基于多色集合理论的机械零件加工路线方法研究[J]. 组合机床与自动化加工技术,2013(9):129-131.

[5] 侯媛彬,高阳东,郑茂全.基于贪心-遗传算法的混合轨迹加工走刀空行程路径优化[J].机械工程学报,2013,49(21): 153-159.

[6] 郝一舒,王德斌,岳滨楠.基于遗传算法的高速铣削加工工艺多目标优化[J].制造技术与机床,2009(6):98-101.

[7] 郑永前,王阳.基于遗传算法的加工工艺决策与排序优化[J].中国机械工程,2012,23(1):59-65.

[8] 李天明. 基于遗传算法对箱体加工工艺的优化设计[J]. 煤炭技术,2009(10):12-14.

[9] 魏文杲. 基于改进遗传算法的工件加工工序优化[J]. 组合机床与自动化加工技术,2010(1):81-83.

[10] 张则强,程文明,钟斌,等.混合品种装配线平衡问题的一种混合搜索机制的蚁群算法[J].机械工程学报, 2009, 45(5): 95-101.

[11] 鲁建厦,蒋玲玲,李修琳.基于混合粒子群算法求解装配线第二类平衡问题[J].中国机械工程,2010,21(4): 420-424.

[12] 张则强,胡俊逸,程文明.第Ⅰ类双边装配线平衡问题的改进蚁群算法[J].西南交通大学学报,2013,48(4): 724-730.

(编辑赵蓉)

Study of Ant Colony Algorithm for Double Screw Compressor End Cover

Machining Process Planning

ZHANG Zheng-wei

(Department of Mechanotronics and Aviation,Zhejiang Institute of Communications,Hangzhou 311112,China)

Abstract：Double screw compressor have excellent stability performance and have been used widely in the mining industry. To meet the requirements of production capacity, using ant colony algorithm to planning it’s machining process procedure by study processing technology of the end cover. In order to guarantee the feasibility of processing scheme, apply the processing constraint and introduce the new “or” type constraint. Finally the algorithm structure of ant colony algorithm is completed by implement the process element sifting module and two heuristic methods in process select module. The key machining process element is find out by study the assembly process of this product. Then the process constraint model of end cover is established and input into the ACO algorithm. So the computer aided process planning is completed. And the effectiveness of this algorithm is proved by contract with the human experience machining plan.

Key words：assembly lines; U- assembly line; particle swarm algorithm; optimization

中图分类号：TH165; TG506

文献标识码：A

作者简介：章正伟(1977—)，男，浙江金华人，浙江交通职业技术学院副教授，硕士，研究方向为CAD/CAM/CAPP/CAE，(E-mail)zzw@zjvtit.edu.cn。

*基金项目：浙江省教育厅2013年度科研计划项目：节能高效低压内置润滑喷油双螺杆压缩主机的研究(Y201329722)；2013年度浙江省高职高专院校中青年专业带头人专业领军项目(LJ2013018)

收稿日期：2015-05-21；修回日期2015-06-19

文章编号：1001-2265(2015)12-0116-05

DOI:10.13462/j.cnki.mmtamt.2015.12.031