基于牛顿插值的主减速器齿侧间隙调节研究*

任永强，洪婉君，任舒蕙

(1.合肥工业大学 机械与汽车工程学院，合肥　230009；2.合肥市第六中学，合肥　230009)



基于牛顿插值的主减速器齿侧间隙调节研究*

任永强1，洪婉君1，任舒蕙2

(1.合肥工业大学 机械与汽车工程学院，合肥230009；2.合肥市第六中学，合肥230009)

摘要：汽车主减速器齿侧间隙调节是通过旋转主齿两端的花螺母进行调整的，然而目前的调整方法均是根据经验手动调节，不仅调节精度有限，而且效率低下。在结合实际生产经验，分析工艺要求后，提出一种自动化调整方案，并运用牛顿插值多项式，拟合调节花螺母与齿侧间隙间的关系函数。同时采用闭环控制实现间隙的有效测量和及时反馈，从而提高控制精度。实践证明：通过数据分析和现场实践，验证所提方案可靠有效，可以提高车间调节效率。

关键词：主减速器；齿侧间隙调节；牛顿插值

0引言

驱动桥主减速器总成是汽车的关键部位之一，其中主减速器在传动系中起降低转速，增大转矩的作用，并通过采用圆锥齿轮传动来改变转矩旋转方向。主减速器的装配质量直接影响汽车运行的平稳性、噪声、寿命及能耗。而汽车后桥减速器的装配质量主要受两个因素的影响，一个是主减速器内主齿总成的装配质量，另一个是主减速器内主、被动齿轮是否啮合良好。

主减速器在高速运转时，由于齿侧间隙的存在，将导致轮齿冲击，这种冲击将带来强烈振动、噪声和较大的动载荷，影响传动寿命和可靠性，因此在装配中，保证齿侧间隙在规定范围内至关重要，工业要求一般为0.15～0.4mm。

齿侧间隙的调整是通过旋转主齿所在轴两端的花螺母，来前后移动主齿，从而改变与锥齿的间隙。由于目前行业的齿侧间隙调整大多为手动调整，因此在实际应用中，花螺母旋转圈数与间隙调整量间的关系一般为操作工人所总结出来的经验公式，而该经验公式多为粗糙的一次线性函数，无法真实体现出二者间的换算关系，这对于具有较高精度要求的齿侧间隙调整工艺来说，将大大增加调整和测量次数，降低工作效率。此外，即便是同种型号的减速箱之间也存在工艺和装配偏差， 因此对于不同的减速箱，其换算公式应该做出一定调整和更新，以更好地提高生产效益。因此本实验平台提出通过牛顿插值多项式对花螺母旋转圈数与齿侧间隙调整量间的关系函数进行拟合，并对往后的调整作出控制。

1试验平台搭建

齿侧间隙测量的一般方法有咬铅法[1]、打表法[1]两种，咬铅法由于受到铁丝自身刚性和测量误差的限制，测量结果往往具有较大的误差。而打表法是在一个齿轮上装有夹紧杆，以测量该齿轮的摆动角度，在千分表上得到度数j，齿侧间隙jn的测量结果直接由计算获得：

式中：R为装夹齿轮的分度圆半径 (mm)；L为百分表触头至齿轮轴线的距离(mm)。

打表法具有较高测量精度，且测量方法便于实现工业自动化，应为未来主流测量方式。本实验平台使用打表法进行齿侧间隙测量。试验平台见图1。

图1　齿侧间隙测量调整试验平台

在测量齿侧间隙时，下方的驱动电机对主减锥齿产生制动力，使其固定不发生旋转。而位移传感器装置的探头下抵主齿上方，随后，主减主齿的加载电机通过加载扭矩转动(左、右方向各一次)主齿，主齿由于齿侧间隙的存在，会发生轻微的偏转，而传感器装置通过杠杆作用，将下方探头左右方向的摆动量按比例传达到上方位移传感器中，并进一步通过串口将数据传入上位机进行处理，从而获得实际的齿侧间隙值。

在调整齿侧间隙时，驱动电机通过对主齿两侧的花螺母旋入/旋出一定圈数来实现对齿侧间隙的调整。而驱动电机旋转圈数是根据间隙调整公式计算得来。

2间隙调整平台的闭环控制系统

按照对被控对象的控制是否具有反馈装置进行分类，可粗略分为开环控制和闭环控制两类。开环控制结构简单、工作稳定，但是抗干扰能力差、控制精度不高；闭环控制由于反馈装置的作用，可以抑制内外扰动对被控量的影响，但对反馈原件的精度要求较高。

为保证齿侧间隙的调节精度和调节效率，该试验平台采用闭环控制。通过位移传感器测量到位移变量，换算后得到实际齿侧间隙值，反馈到上位机系统中，构成闭环控制系统，详见图2。

图2　闭环控制系统

3间隙调整设定值与实际调整偏差分析

该试验平台通过位移传感器测得主减速器中主齿与锥齿的间隙值，将此间隙值与设定值进行比较，得到一个偏差值，再对控制输入量进行调整， 将两次测量值相比较可以获得实际间隙调整值，而该实际调整值经过上位机处理过后，将作为驱动电机控制信号反馈到PLC中，进而反馈到变频器中，形成对驱动电机的闭环矢量控制。变频器在获得调整值后，驱动左右两侧的电机旋入/旋出主齿两侧的花螺母，进而再对齿侧间隙进行调整。

正如上方所说，需调整的花螺母圈数与间隙调整量之间存在换算关系，但是由于换算公式存在难以估计和消除的误差，因此间隙调整无法一次到位，总是存在调整偏差，这时，通过闭环控制便可以对偏差进行反馈和调整。

4牛顿插值

由于花螺母实际旋转圈数与实际齿侧调整量间的函数关系是未知的，因此需要在测量调整中通过数据处理拟合出关系函数。该试验目的是为了尽可能降低测量和调整次数，因此，需要通过少数的几次测量数据来构建拟合函数，而插值法适用于少点函数拟合情况，因此本实验采用插值法进行函数构建。

在各种插值法中，牛顿插值利用插商、差分的概念，以x0,(x-x0),(x-x0)(x-x1),……为基本项，通过离散函数点构建插值多项式pn，以实现对原函数的拟合。与逐次线性插值法相比，牛顿插值法同样具有有效计算任何给定点函数值的优点，但其统一表达式的特性摆脱了每一段都需要特定插值表达式的缺陷。此外，与Lagrange多项式相比，它克服了“每增加一个点时整个计算工作重新开始”的缺点，减少乘除法的运算次数。因此本研究最终决定采用牛顿插值法进行函数拟合。

设齿侧间隙调整量为x，而实际旋转圈数为f(x)，每一次齿侧间隙测量调整都可以获得一组(x,f(x))数据，基于这些数据可以通过牛顿插值多项式拟合f(x)函数。控制系统再通过拟定的f(x)函数输出控制值。

牛顿插值多项式原理如下：

已知f(x0),f(x1),f(x2),…,f(xn)，其中 x0,x1,x2,…,xn彼此互异，则函数f(x)=pn(x)+rn(x)，其中pn(x)为插值多项式，即本实验的拟合函数，rn(x) 为牛顿插值余项，此处忽略不讨论，因此 f(x)≈pn(x)。为满足插值条件 pn(xi)=f(xi),i=0,1,…,n, 牛顿插值多项式定义如下：

pn(x)=f(x0)+f[x0,x1](x-x0)+

f[x0,x1,x2](x-x0)(x-x1)(x-x2)+

f[x0,x1,…,xn](x-x0)(x-x1)…(x-xn)

pn(x)多项式中的

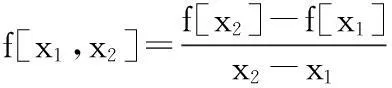
以此类推……求出插商表(见表1)中的各个插商值，通过这些插商值可求得 f(x) 的牛顿插值多项式 pn(x)。

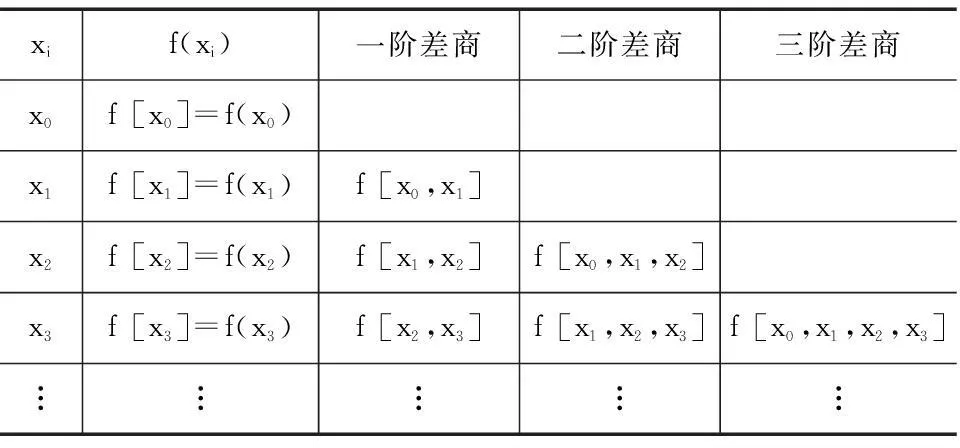
表1　牛顿插商表

插商表中对角线上的插商值就是牛顿插值多项式的各项系数。

5牛顿插值拟合实现

控制系统的数据处理通过上位机完成，上位机最终将控制数据通过以太网发送给PLC，再进一步输出到变频器中，从而实现对驱动电机的控制。本实验台上位机拟合函数的构建与实现由C#语言编写，其流程图见图3。

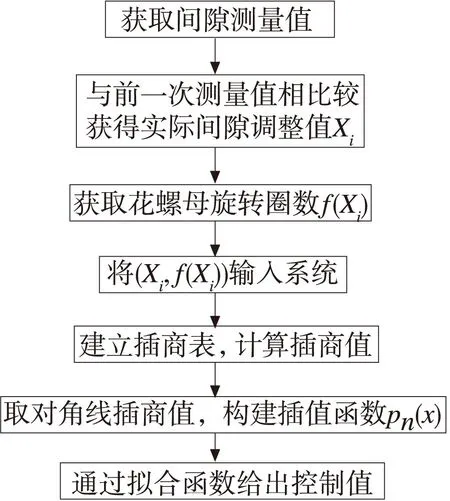
图3　牛顿插值算法流程图

每当获取新的间隙测量值和旋转圈数时，新值都将输入系统，然后重新构建拟合函数，随着测试次数增多，拟合函数将越逼近实际函数曲线。

6实验结果

把得到的拟合函数通过500个点在界面中绘制出来，便于试验观察。图4中为其中一个减速箱三次测量调整后拟合的函数结果。

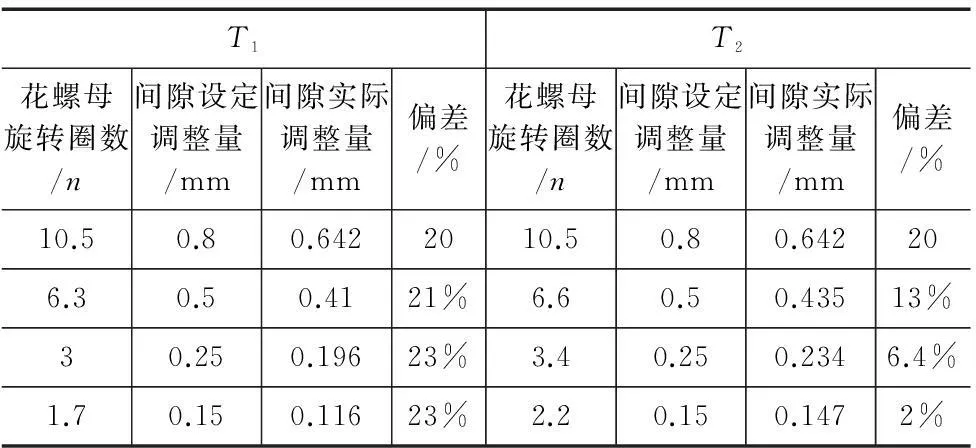
试验数据如表2所示，其中T1是使用经验公式调节间隙量的实验数据，T2是使用牛顿插值法所得的实验数据。 从实验数据中可得：经验公式随着调整量减小，其控制偏差有变大的趋势，而牛顿插值构建的函数可以有效反映花螺母旋转圈数与齿侧间隙调整量间的关系，随着实验次数增多，控制精度也在不断变高。

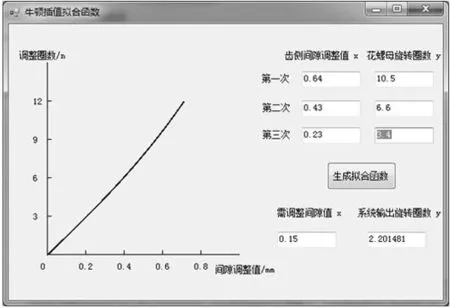
图4　函数拟合结果

T1T2花螺母旋转圈数/n间隙设定调整量/mm间隙实际调整量/mm偏差/%花螺母旋转圈数/n间隙设定调整量/mm间隙实际调整量/mm偏差/%10.50.80.6422010.50.80.642206.30.50.4121%6.60.50.43513%30.250.19623%3.40.250.2346.4%1.70.150.11623%2.20.150.1472%

7总结

通过牛顿插值多项式，对花螺母旋转圈数与齿侧间隙调整量间的关系进行拟合，可以有效反映二者间的函数关系。本研究方法在实际生产应用后，结果表明，与传统经验公式相比，该方法显著提高了齿侧间隙的调整效率。并且，试验中所得到的牛顿插值多项式公式可以为日后齿侧间隙调整的深入理论分析提供基础。

[参考文献]

[1] 常国强，高勇.齿轮啮合间隙测量方法探讨[J].计量与测量技术，2011,38(6):38-39.

[2] 尚姣，冯慧华，鲁守卫，等.轿车变速器主减速器齿轮副动态性能仿真[J].振动工程学报，2010,23(6):665-669.

[3] 蔡火用，白峰衫.高等数值分析[M]. 北京：清华大学出版社,1998.

[4] 濮良贵，纪名刚.机械设计 [M].8版.北京：高等教育出版社，2006.

[5] 孙智民，季林红，沈允文,等.齿侧间隙对星型齿轮传动扭振特性的影响研究[J]. 机械设计,2003,20(2):3-6.

[6] 王义.汽车变速箱齿轮接触分析与修形研究[D].沈阳：东北大学，2010.

[7] 吴士鹏，徐蕾，俞建卫.模糊PID在CNC粉末液压机控制系统中的应用研究[J].组合机床与自动化加工技术，2013(12):60-63.

[8] 李惠彬，郑兆昌.带有侧隙的齿轮故障振动[J].清华大学学报(自然科学版),2001,41(6):104-107.

[9] 王维，杨建国.基于插值算法的数控机床复合误差补偿技术[J].上海交通大学学报，2014,48(1):12-21.

[10] 葛彩夏，邹开其.模糊牛顿插值与模糊样条函数的表示[J].模糊系统与数学，1995,9(4):85-90.

(编辑赵蓉)

Research of Gear Backlash Adjustment in Main Gear Box Based on Newton Interpolation

REN Yong-qiang1, HONG Wan-jun1, REN Shu-hui2

(1.School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei 230009, China;2.Hefei No.6 High School,Hefei 230009,China)

Abstract：The gear backlash of main gear box is adjusted by rotating knurled nuts which are located on the either side of the main gear. However, the current general adjustment method is adjusting manually from experience which usually caused low precision and efficiency. Based on the actual production experiences and analysis of process, an automotive adjustment solution is put forward. Then, Newton interpolation method is proposed as a curve fitting method which describes the functional relationship between adjusting knurled nut and gear backlash. And to improve control accuracy, the control system used closed-loop control to realize the efficiency of measurement and timely feedback. Through data analysis and field application, this system is proved to be reliable and efficient on improving adjustment efficiency.

Key words：main gear box; gear backlash adjustment; Newton interpolation

中图分类号：TH161；TG506

文献标识码：A

作者简介：任永强 (1968—)，男，浙江东阳人，合肥工业大学副教授，博士，研究方向为机电控制与自动化、汽车装备及其自动化、误差精密测量与补偿，(E-mail) ryqiang@aliyun.com。

*基金项目：国家科技支撑项目 (2012BAF06B01)；国家智能制造装备发展专项项目(发改办高技[2011]2548号)

收稿日期：2015-01-14

文章编号：1001-2265(2015)12-0078-03

DOI:10.13462/j.cnki.mmtamt.2015.12.021