遗传禁忌搜索算法在工业机器人结构参数辨识上的应用*

熊　杰，杨东升，王允森

(1.中国科学院大学，北京　100049；2.中国科学院 沈阳计算技术研究所，沈阳　110168)



遗传禁忌搜索算法在工业机器人结构参数辨识上的应用*

熊杰1,2，杨东升2，王允森1,2

(1.中国科学院大学，北京100049；2.中国科学院 沈阳计算技术研究所，沈阳110168)

摘要：针对工业机器人标定过程中的结构参数辨识方程形式复杂、计算繁琐等问题，提出一种采用遗传禁忌搜索算法来寻求辨识方程的最优解的方法。首先采用遗传算法做全局搜索，为加快收敛速度，遗传算法的选择算子、交叉算子和变异算子的参数按照动态适应的方式进行。遗传算法调用结束后，将种群的最优个体作为禁忌搜索的初始解，调用禁忌搜索算法做进一步局部搜索。为了提高解的精确性，邻域半径根据适应度值进行动态调整。仿真实验结果表明遗传禁忌搜索算法能够有效的得到结构参数的完全辨识。

关键词：工业机器人；参数辨识；遗传算法；禁忌搜索

0引言

机器人重复定位精度很高，但绝对定位精度一般较差，这是因为制造误差、关节磨损、环境条件等因素导致机器人实际结构参数和理论结构参数不一致的原因造成，一般采用标定技术提高绝对精度。机器人标定包含运动学建模，位姿测量，参数辨识，误差补偿四个过程。通常参数辨识是求解一组非线性方程的过程[1]，直接求解十分复杂甚至是低效的。传统的方法[2-5]等只考虑末端的位置信息，按照测量点的位置约束建立起一组线性方程组，简化了求解过程，但是这种方法建立的方程组部分列是线性相关的，并不能做到结构参数的完全辨识。

随着激光跟踪技术的发展，机器人末端位姿的测量变得相对容易，因此可以利用位置和姿态信息进行结构参数的完全辨识。由于辨识方程的复杂性，很多学者尝试以智能算法[6-8]求解，取得了一定的效果。遗传算法(GA)[9]作为一种性能优异的全局优化算法。该算法通过对父代种群进行选择，交叉，变异等操作，按照优胜劣汰，适者生存的进化规则，不断得到更优的群体。该算法具有固有的并行性，搜索效率高，但是也存在着易于早熟，爬山能力弱，局部搜索能力差等缺点。禁忌搜索(TS)[10-11]是一种扩展了的局部搜索技术，通过引入一个禁忌表和相应的禁忌准则来避免重复搜索，并通过特赦准则以赦免部分被禁忌的优良解，在搜索过程中，可以接受劣质解，从而可以跳出局部最优。但是禁忌搜索是串行的，对初始解有较强的依赖性，而且搜索效率低。

本文结合GA和TS的特点，在对机器人运动学建模之后，将结构参数辨识的过程分为两个阶段，先采用GA做全局搜索，得到全局概要解，作为TS的初始解，然后采用TS做局部搜索，进一步改善所得解。仿真表明，该方法可以有效的得到结构参数的完全辨识。

1运动学建模

目前应用最广泛的机器人运动学模型是DH模型，根据DH模型所建立的相邻关节之间的齐次变换矩阵为：

Ai=Rotz(θi)Tranz(di)Tranx(ai)Rotx(αi)

(1)

其中θi表示关节旋转，di为连杆长度，ai为关节偏移，αi为连杆扭转，i=1…N，N为关节连杆的个数。当相邻关节平行或近似平行时，轴线的微小的偏移会引起连杆距离di的极大变化，此时通常使用Hayati所提出的MDH模型[12]。MDH模型在Ai中添加了绕Y轴旋转的扭角βi，即：

Ai=Rotz(θi)Tranz(di)Tranx(ai)Rotx(αi)Roty(βi)

(2)

当相邻连杆平行或近似平行时，di=0；否则，βi=0。确定了各关节之间的变换矩阵之后，那么按照机器人正运动学模型，其末端位姿可以表示为：

(3)

其中，θ=(θ1,…θN)，d,a,α,β同理，表示为结构参数的向量。

由于装配因素、负载因素、环境因素以及磨损变形等原因，各关节的实际参数和理论参数之间存在参数误差[Δθi,Δdi,Δai,Δαi,Δβi],i=1…N，所以机器人的实际运动学模型可以修正为：

Tr=F(θ+Δθ,d+Δd,a+Δa,α+Δα,β+Δβ)

(4)

Tr表示末端的实际位姿，T表示末端的理论位姿。注意到Tr,T都是4×4的方阵，为便于计算，将姿态部分采用rpy角形式描述，这时Tr,T可以转化为6×1的向量，即[px,py,pz,r,p,y]′，将转化后的Tr,T分别记为Pr,P。因为Δθ,Δd,Δa,Δα,Δβ值实际上都比较小，所以ΔP可以表示为:

ΔP=Pr-P=

(5)

表示成矩阵的结构即为：

(6)

机器人运动学结构参数辨识就是要求出Δx的值。Δx的求解需要计算J的逆，这一过程非常复杂且需要耗费大量的时间计算。本文将其视作多参数的优化问题，采用遗传禁忌搜索算法求解该问题的最优解，从而得到实际结构参数。

2遗传禁忌搜索算法

2.1遗传算法做全局搜索

遗传算法是一种模拟生物在自然环境中的遗传和进化行为而形成的具有全局搜索能力的仿生优化算法。本文将各连杆参数的误差值作为种群的个体，将进化得到的个体修正机械臂的运动学参数，然后更新运动学模型，取末端执行器的实际位姿和更新后的运动学模型计算得到的理论位姿之间的差值作为适应度函数。根据适应度函数对个体进行选择，交叉，变异操作，得到新一代个体。由于适应度好的个体能够以更大的概率保留下来，而适应度差的个体逐渐被淘汰，从而使得种群得到进化。遗传算法的初始化及相关算子设定如下。

个体编码及初始种群：将[Δθi,Δdi,Δai,Δαi,Δβi],i=1…N作为种群的个体，采用实数编码，按照结构参数误差经验值的三倍设置个体变量的上下界。随机初始化种群。

适应度函数：设观测集中样本数量为Ns，那么适应度函数设为所有样本的误差距离之和：

(7)

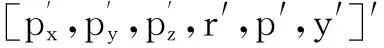
选择算子：将当前种群中适应度高的个体按照一定的选择压差遗传到下一代。选择压差设置的过大，会导致适应度低的个体很快被淘汰，从而可能产生早熟现象。所以在进化的初期压差应该设置的较小，以保证多样性；进化的后期压差选择大一些，以加快收敛。可以采用如下动态的方式确定选择压差：

Press(i)=1+i/MAXGEN

(8)

i表示当前进化的代数,MAXGEN表示最大代数。

交叉算子：在进化初期，希望交叉概率较大，能够迅速对种群优化；在进化后期，希望交叉概率较小，这样能够使得优秀个体不被破坏。所以可以动态的设定交叉率:

Pc(i)=Pc(0)(1-i/MAXGEN)2

(9)

其中，Pc(0)表示预设的交叉率，通常取之间。

变异算子：在进化初期，应该加大突变率，以提高优良个体的产生，在进化后期，应该减少突变量，防止好的基因丢失，所以可以动态设定变异率，

Pm(t)=Pm(0)-(Pm(0)-Pmin)·i/MAXGEN

(10)

其中，Pm(0)表示预设的变异率，Pmin表示变异率允许的最小值。

综上，采用遗传算法求解机器人结构参数误差的整体算法流程如图1所示。

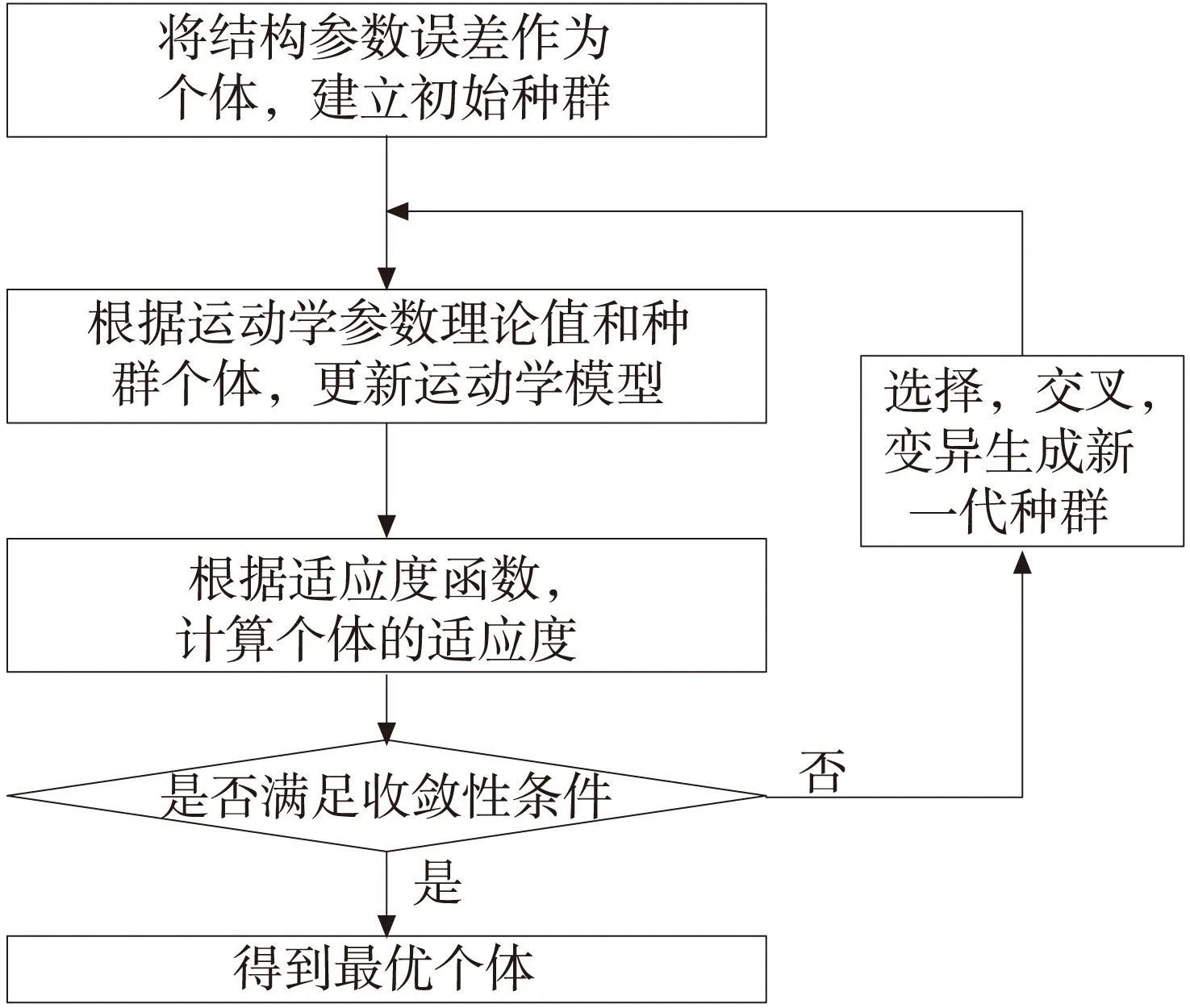
图1　遗传算法流程图

图1描述了GA的整体流程，但是由于遗传算法的局部搜索能力较差，易早熟收敛，所以必须对终止种群的最优个体进一步做局部搜索。这里采用禁忌搜索算法进一步求最优解。

2.2禁忌搜索算法做局部搜索

禁忌搜索是一种启发式迭代算法[11]，通过一种邻域规则得到当前点的邻域集，引入禁忌表的概念，避免对局部最优解的重复搜索，并采用特赦规则移除对优良个体的禁忌。在进一步求解运动学结构参数的过程中，禁忌搜索相关的参数设定如下。

邻域规则：在搜索初期，适应度较差，此时邻域半径应该选择的大一些，这样可以加快收敛，在搜索后期，适应度较好，此时应该减小邻域半径，以得到更加精确的解。采用超矩形环形成当前解的邻域，其中，邻域的大小与当前的适应度大小动态调整。其定义如下：

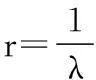
(11)

其中r为邻域半径，FieldR是个体变量的上下界的差向量。fitness是适应度值，是邻域半径调节的参数。记x为当前解，这样，邻域的超矩阵环就可以定义为：

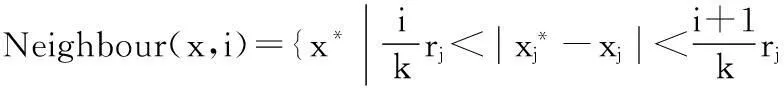
i=0,1…k-1,j=1,2…4N}

(12)

其中，Neighbour(x,i)表示x邻域内的第i个环，xj表示个体中的第j个变量，k表示邻域中设置的矩阵环的数量。在每个环中随机的选取一定数量的点，形成当前解的邻域集。

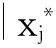
终止规则：一般情况下可以设定一个最大迭代步数，或者在一个给定的迭代步数内算法搜索到的最优解没有改进时，算法将终止计算。

采用禁忌搜索进一步求解机器人结构参数误差的算法流程如图2所示。

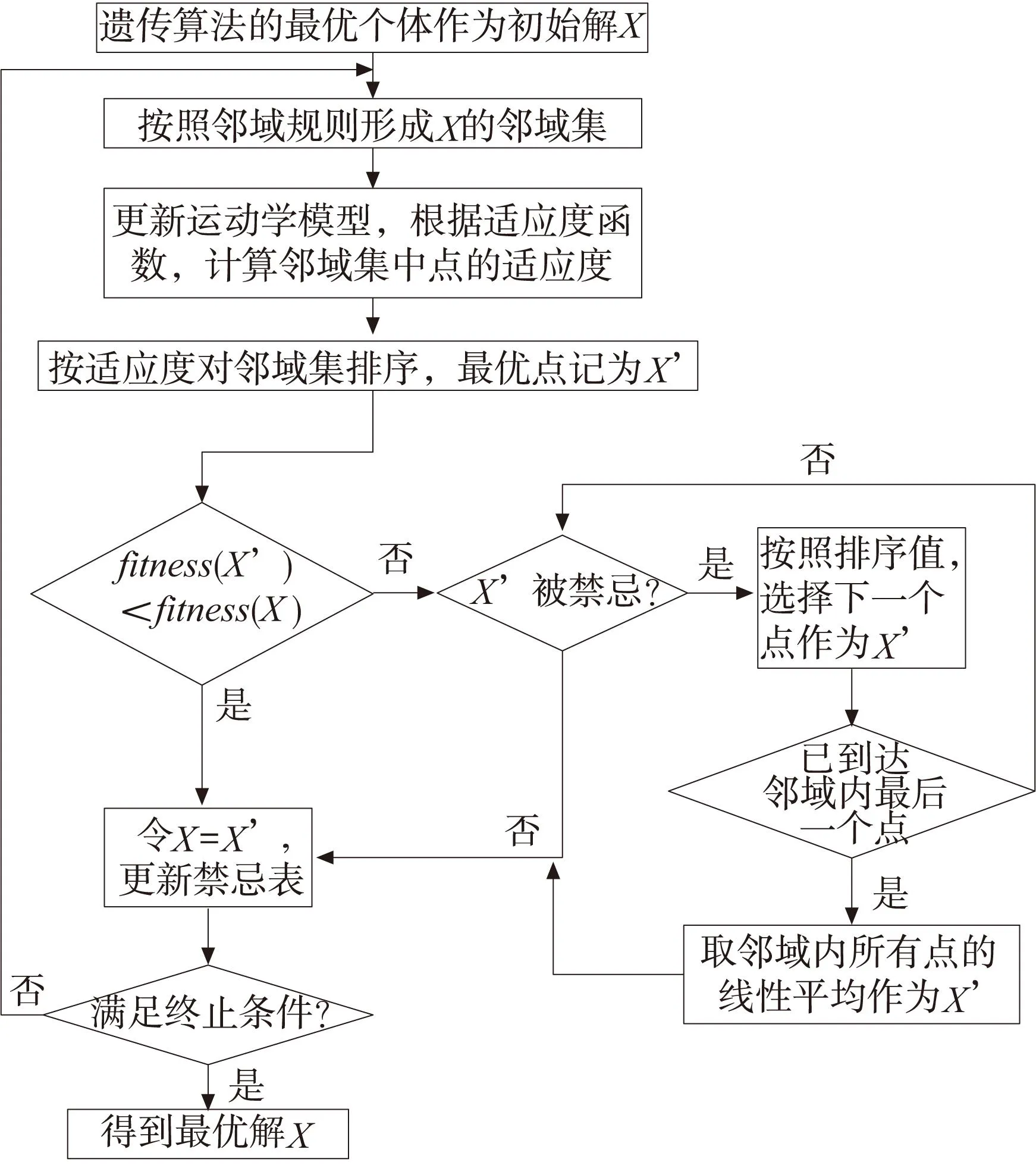
图2　禁忌搜索算法流程图

3仿真

3.1机器人模型

在matlab中实现GTSA算法，仿真过程中所使用的机器人模型为MOTOMAN-MH6。该机器人为6R型，构型如图3所示，结构参数取值如表1所示。

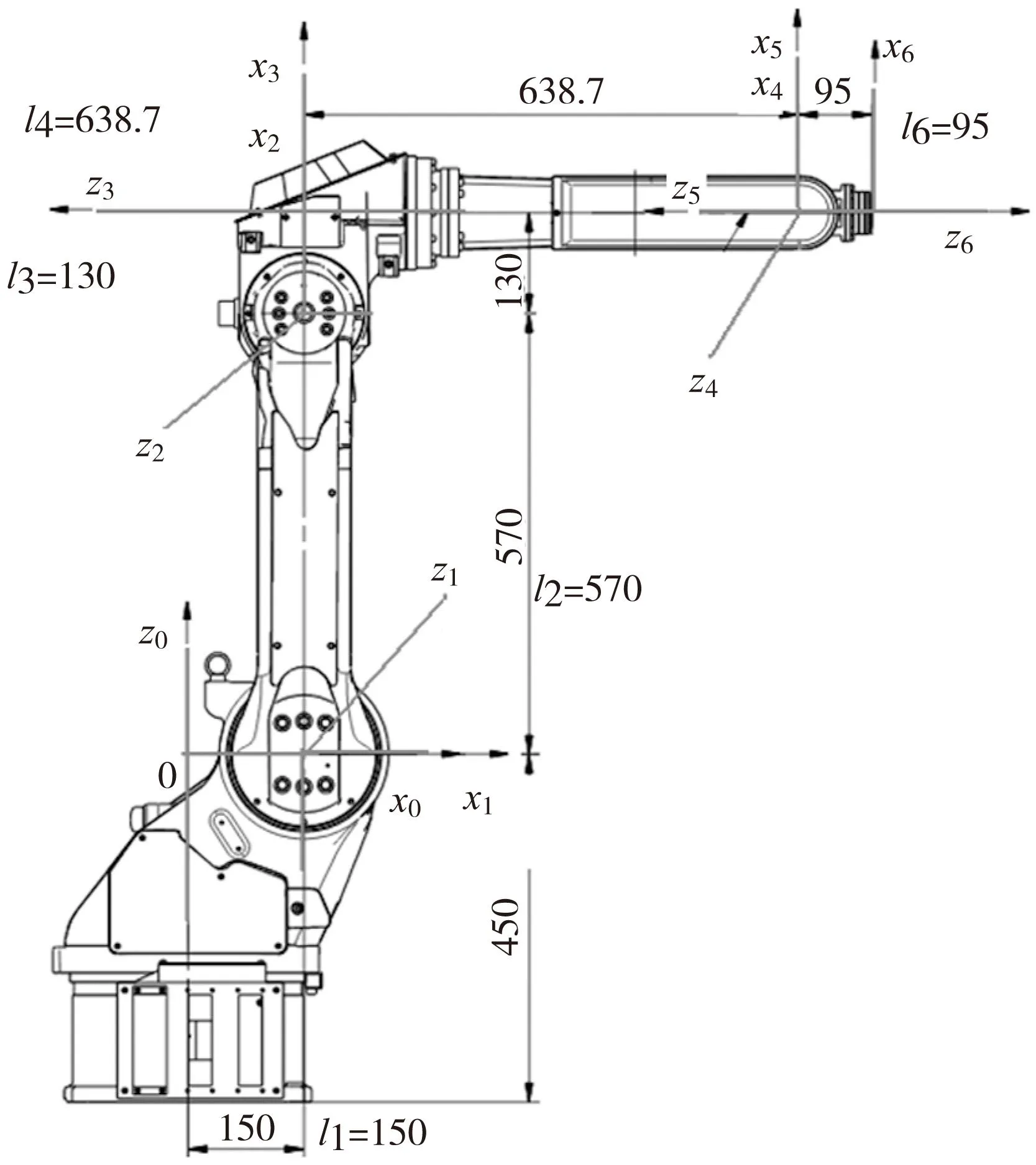
图3　MOTOMAN-MH6运动学坐标系

从表1中可以看出，该机器人第2和3关节相互平行，所以运动学模型应该采用MDH方法，在第二关节引入绕y的转角β2，然后基于表1即可构造出机器人的理论运动学模型。因为在实际环境中，机器人的实际结构参数和理论参数之间总是存在一定的误差，所以可以根据表2预设的结构参数误差建立机器人的实际运动学模型。采集70组理论位姿点和对应的实际位姿点，选择其中50组作为训练集，20组作为测试集。训练集作为GTSA算法的输入，调用GTSA算法反解出结构参数误差。

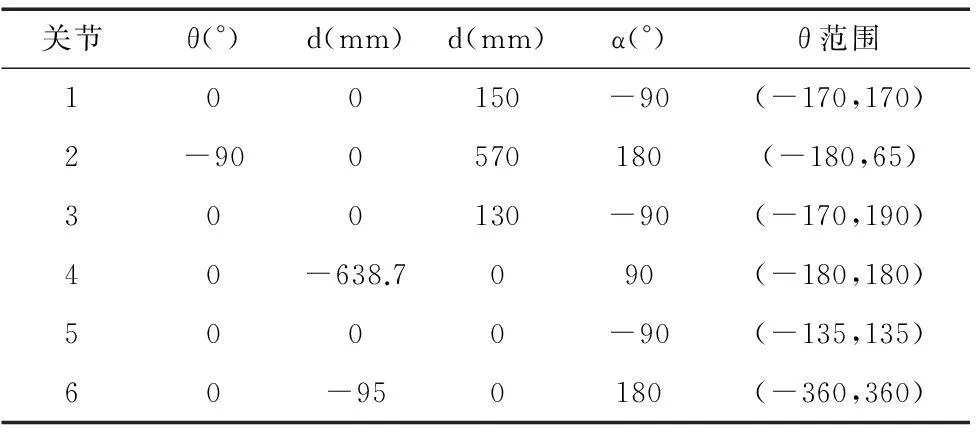
表1　MOTOMAN-MH6运动学结构参数

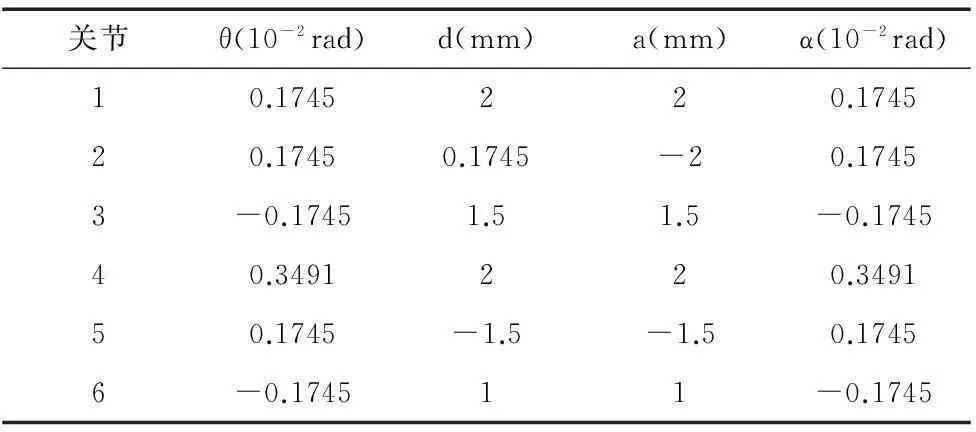
表2　预设的结构参数误差(d2表示β2)

3.2基于GA的全局搜索

MOTOMAN-MH6为6R型机器人，共24个结构参数，则种群个体为1×24的行向量，随机初始化种群，种群中个体数量取40。初始交叉率设为0.95，初始变异率设为0.2，最小变异率设为0.05，迭代300次后得到的结果如图4所示。

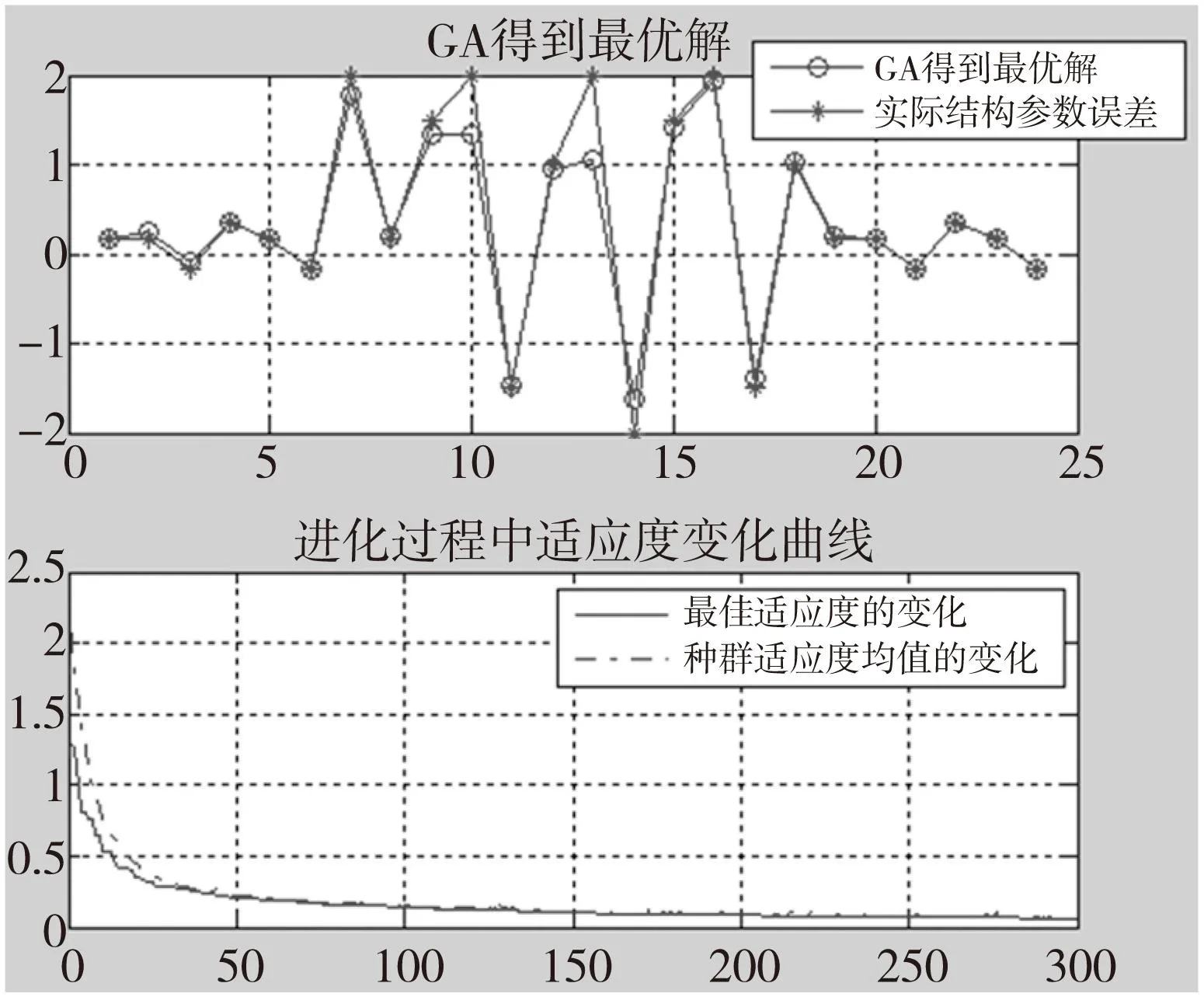
图4　种群最优个体以及适应度变化曲线图

从图4中可以得出，整体上，种群朝着适应度值下降的方向进化，200代以后，最佳适应度和平均适应度已经基本重合，这表明种群已经出现早熟现象。GA得到的最优解中，θ,α,β计算的较为准确，而d,a计算误差较大，这是因为θ,α,β的误差对末端位姿产生的影响更显著。

3.3基于TS的局部搜索

将GA算法中得到的最优解作为TS的初始解。邻域半径调节参数，超矩形环的个数k=4，在每个环中随机选择5个点，故一个点的邻域集可以形成20个点。禁忌表大小设为40，禁忌长度设为36。迭代2500次，TS算法中适应度值的变化曲线如图5所示，以及得到的最优解如表3所示。

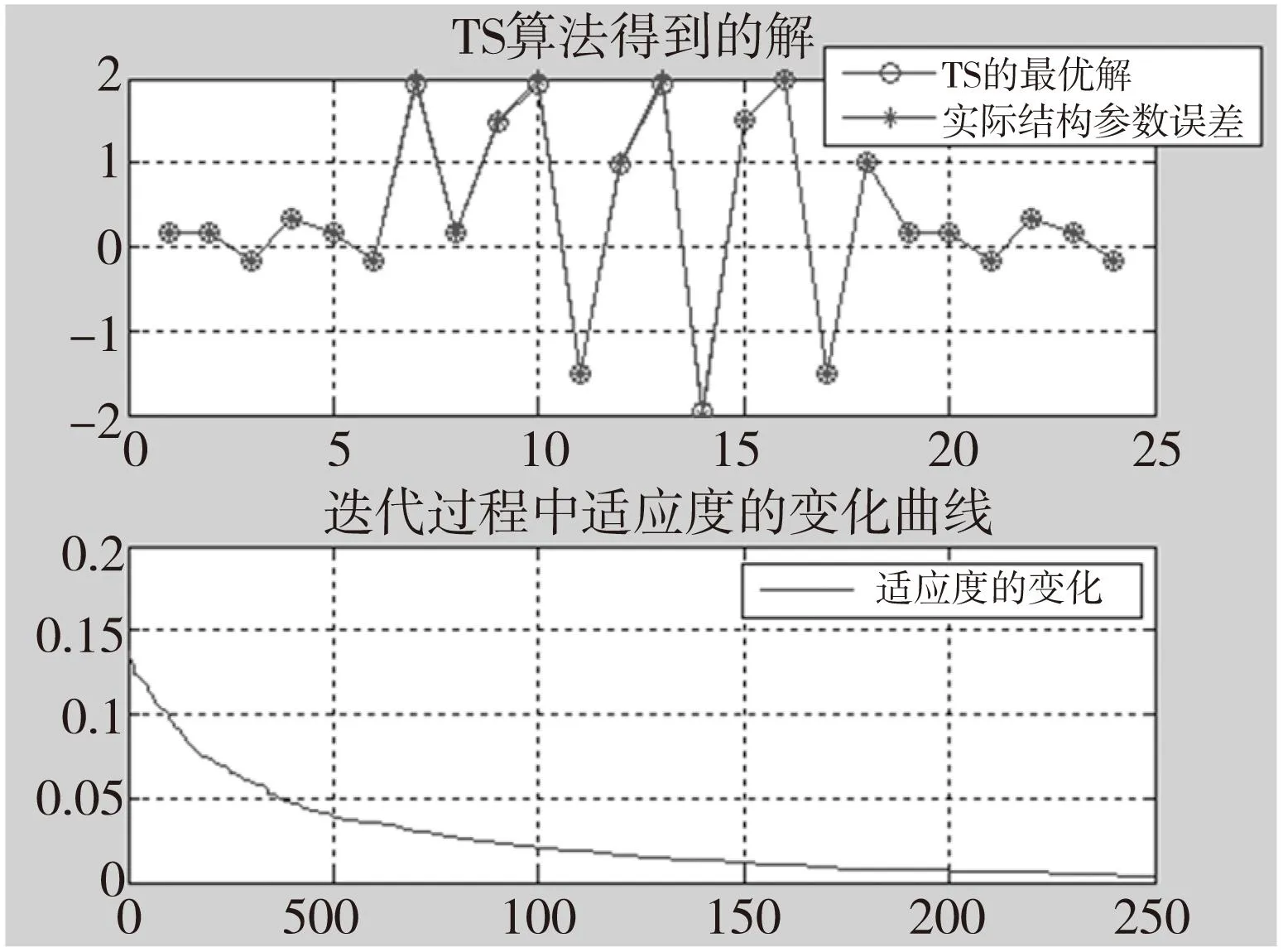
图5　TS算法最优解以及适应度变化曲线图

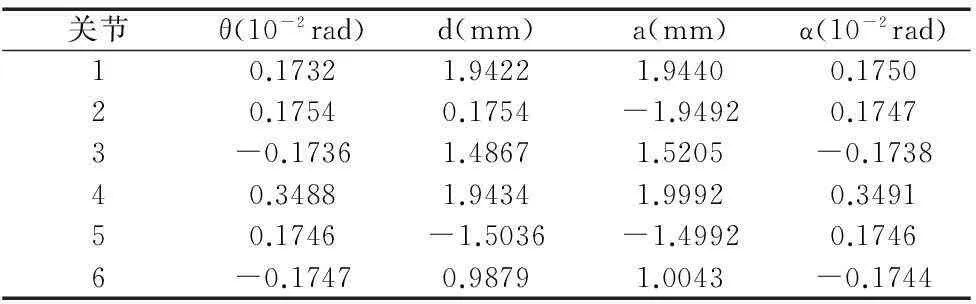
关节θ(10-2rad)d(mm)a(mm)α(10-2rad)10.17321.94221.94400.175020.17540.1754-1.94920.17473-0.17361.48671.5205-0.173840.34881.94341.99920.349150.1746-1.5036-1.49920.17466-0.17470.98791.0043-0.1744

从图5和表3中可以看出，在GA的基础上，TS得到的最优解能够更加逼近真实解。将TS得到的最优解修正机器人的运动学结构参数，在测试集上计算实际位姿和修正后的理论位姿之间的欧式距离，修正前和修正后的对比图如图6所示。

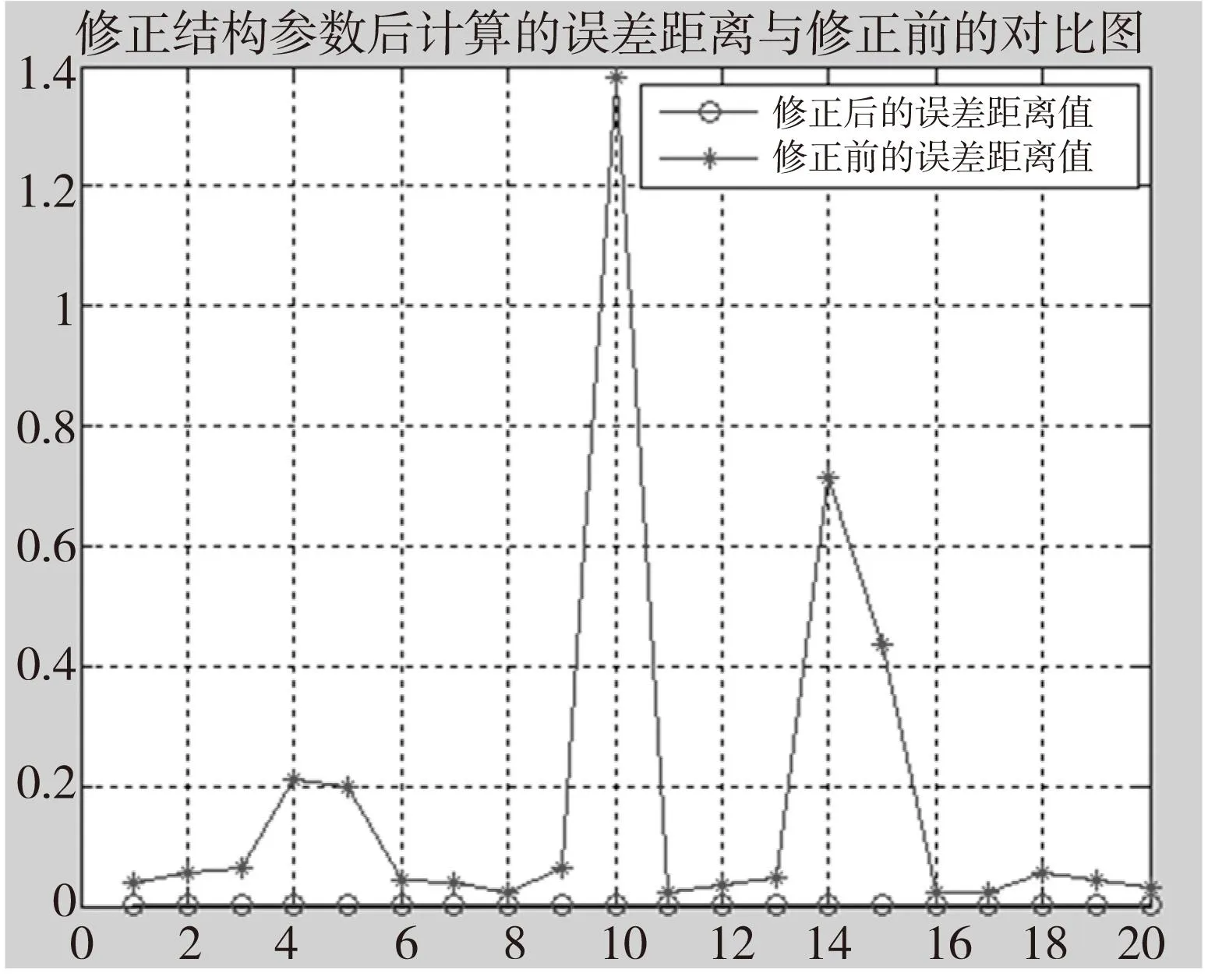
图6　修正结构参数后计算的误差距离与修正前的对比图

由图6可知，修正后，理论位姿和实际位姿之间的误差减少到几乎为0，说明GTSA得到的解是有效的。

4结论

本文针对机器人结构参数辨识方程形式复杂，直接求解计算繁琐的问题，提出采用遗传禁忌搜索算法得到机器人的结构参数误差值。该算法无需求解逆运动学，可以处于离线状态下进行，整体上简化了辨识过程，仿真结果表明该算法是有效性的。当然，该算法也有一些不足之处，比如，辨识的结果精度依赖于测试集的选取。所以在实际实验中，必须建立起足够的测试数据，同时尽可能减少观测噪声，并且要注意使测试集均匀分布于机器人的整个工作空间。

[参考文献]

[1] 王琨. 提高串联机械臂运动精度的关键技术研究[D]. 合肥:中国科学技术大学, 2013.

[2] 刘振宇, 陈英林, 曲道奎, 等.机器人标定技术研究[J]. 机器人,2002,24(5):447-450.

[3] 童上高,李权峰,龚潇,等. 码垛机器人运动定位误差补偿[J]. 组合机床与自动化加工技术,2012(5):65-69.

[4] 吴蒙蒙,许兆棠,吴海兵,等. 环境温度影响下并联机床的加工误差解耦[J]. 组合机床与自动化加工技术,2014(6):4-7.

[5] Zhang T, Du L, Dai X. Test of Robot Distance Error and Compensation of Kinematic Full Parameters[J].Advances in Mechanical Engineering,2014,2014:1-9.

[6] 丁度坤. 工业机器人智能运动控制方法的分析与研究[D].广州:华南理工大学,2010.

[7] 汪霖,曹建福,韩崇昭. 基于粒子群优化的机器人多传感器自标定方法[J].机器人,2009,31(5):391-396.

[8] 周炜,廖文和,田威,等. 基于粒子群优化神经网络的机器人精度补偿方法研究[J].中国机械工程,2013,24(2):174-179.

[9] 边霞,米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究,2010,27(7):2425-2429,2434.

[10] 张晓菲,张火明. 基于连续函数优化的禁忌搜索算法[J]. 中国计量学院学报,2010,21(3):251-256.

[11] 王明兴. 连续禁忌搜索算法改进及应用研究[D]. 杭州:浙江大学, 2005.

[12] Hayati R.Robot Arm Geometric Link Parameter Estimation[J]. Proceedings of The 22nd IEEE Conf. on Decision and Control, 1983,12: 1477-1483.

(编辑赵蓉)

Application of Genetic-Tabu Search Algorithm in Industrial Robot Structural Parameter Identification

XIONG Jie1,2，YANG Dong-sheng2，WANG Yun-sen1,2

(1.University of Chinese Academy of Sciences,Beijing 100049, China; 2.Shenyang Institute of Computing Technology, Chinese Academy of Sciences,Shenyang 110168, China)

Abstract：For structural parameter identification problems with industrial robot calibration, considering the identification equations tends to form complexes, tedious calculation, so a genetic-tabu search algorithm(GTSA) for the optimal solution of identification equation was proposed. Firstly, genetic algorithm(GA) was used to global search. To accelerate the convergence speed of GA, the selection operator, crossover operator, mutation operator parameters was deal with the dynamic adaptive way. After GA called, the best individual in the population would be treated as the initial solution to tabu-search(TS). Then TS was called for further local search. In order to improve the accuracy of the solution, the neighborhood radius dynamically adjusted based on the fitness value. Through simulation experiment, the results show that GTSA can effectively get the full identification of structural parameters.

Key words：industrial robot; parameter identification; genetic algorithm; tabu search

中图分类号：TH166;TG659

文献标识码：A

作者简介：熊杰(1990—)，男，河南南阳人，中科院大学硕士研究生，研究方向为机器人标定技术，(E-mail)xiongjiezk@163.com；杨东升(1965—)，男，中国科学院沈阳计算技术研究所研究员，博导，研究方向为数控系统，现场总线，机器人，(E-mail)dsyang@sict.ac.cn。

*基金项目：核高基专项(2012ZX01029-001-002)

收稿日期：2015-02-12；修回日期：2015-03-12

文章编号：1001-2265(2015)12-0004-04

DOI:10.13462/j.cnki.mmtamt.2015.12.002