基于自适应分数阶微积分的图像去噪与增强算法

李　博, 谢　巍

(华南理工大学自动化科学与工程学院, 广东 广州 510641)



基于自适应分数阶微积分的图像去噪与增强算法

李博, 谢巍

(华南理工大学自动化科学与工程学院, 广东 广州 510641)

摘要：针对传统的图像去噪算法容易忽视图像纹理细节的问题,首先提出一种全局自适应分数阶积分去噪算法。该算法可以在去除图像噪声的同时,对图像的纹理进行一定的保留。其次在全局自适应分数阶算法的基础上,针对一类低强度椒盐噪声提出另一种基于小概率策略的自适应分数阶微积分图像去噪与增强算法,该算法将图像中噪声点的出现视为小概率事件并进行分割,然后再采用自适应分数阶积分对噪声点进行处理的同时,采用自适应分数阶微分对图像的纹理进行增强和保留。实验结果表明,两种方法都可以达到较好的去噪效果,其中基于小概率策略的自适应分数阶算法在去噪的同时更具有增强图像的边缘的效果。

关键词：分数阶; 自适应; 图像去噪; 图像增强; 梯度; 阶次

0引言

数字图像在采集和传输的过程中不可避免的受到噪声的影响,导致后续的分割和识别等图像处理过程中出现一定的困难,因此图像去噪算法的研究是数字图像处理中的一项重要内容。国内外学者已经提出了几种经典的图像去噪算法,如文献[1]中的非局部均值滤波、文献[2]中的卡尔曼滤波、文献[3]中的小波图像去噪,以及由中值滤波、低通滤波、维纳滤波衍生而来的其他方法等[4-5]。上述方法虽然都能在不同程度上去除图像的噪声,但是这些图像去噪算法都直接或间接地在去噪模型的构建中采用了整数阶积分,这样会在去除噪声的同时损失图像的边缘和纹理等细节信息。近年来,将分数阶微积分[6-8]引入图像处理成为了一个新颖的研究方向[9-10]。分数阶微分(分数阶的阶次为正数时)具有增强图像边缘的同时保留一定的图像弱纹理等特点[11-13],分数阶积分(分数阶的阶次为负数时)能够在去除图像噪声的同时保留一定的图像纹理信息。文献[14-15]将分数阶引入全变分模型以在去噪的同时更好地消除图像阶梯效应,文献[16-17]提出的基于Riemann-Liouville和Grunwald-Letnikov定义的分数阶积分去噪算法,能够在去除噪声的同时保留一定的图像边缘和纹理,但是由于该算法对全局图像都是采用人为指定的同一积分阶次,因此在处理不同强度的噪声和图像纹理时,都只能依据同一阶次的频率响应曲线,难以达到较好的去噪效果。

本文基于分数阶微积分理论提出了两种图像去噪与增强算法。首先,是一种全局自适应分数阶积分去噪算法(该算法针对几类常见的噪声图像),该算法对图像中的每一个像素点都进行分数阶积分运算,每个像素点的最佳积分阶次由该点8个方向上的平均梯度来确定,然后根据最佳阶次的频率响应曲线对该像素点进行处理,从而达到较好的去噪效果。其次,由全局自适应分数阶积分去噪算法的实验结果发现该算法对一类椒盐噪声图像去噪效果较好,所以本文在全局自适应分数阶积分去噪算法的基础上进一步提出另一种基于小概率策略的自适应分数阶图像去噪算法(该算法只针对一类较低强度的椒盐噪声图像),该算法将图像中出现的椒盐噪声点定义为小概率事件并进行分割,然后采用自适应分数阶积分对分割出来的噪声点进行处理的同时,采用自适应分数阶微分对图像的边缘和纹理进行增强与保留,从而使处理后的图像同时具有较好的去噪效果和增强效果。

1相关理论引导及分析

1.1分数阶微积分定义

至今为止,分数阶微积分还没有统一的定义表达式,数学家们从各自不同的角度去分析问题,得到了不同的定义。现阶段主要的3种分数阶微积分定义:Grunwald-Letniko定义(G-L)、Riemann-Liouville定义(R-L)和Capotu定义[18-20],G-L定义由整数阶微分的差分定义推导而来,而R-L和Capotu定义由整数阶积分的柯西公式推导而来。

利用Gamma函数Γ(x)可以将微积分阶次从整数推广到分数,[·]表示整数部分,f(x)的变化区间为[a,b], G-L定义的v阶次分数阶微积分为

(1)

R-L定义的v阶次分数阶积分为

(2)

1.2分数阶掩模的实现

将分数阶积分理论引入图像去噪是一个新的发展方向,若一元信号f(t)的持续期为t∈[a,t],将信号持续时间按间隔h=1等分,那么n=[(t-a)/h]=[t-a]。当v<0时,在G-L定义下一元信号f(t)的分数阶积分的近似表达式:

(3)

R-L定义下一元信号f(t)的v阶次积分的近似表达式:

(4)

分别沿着二维数字图像像素点的8个方向(0°, 45°,90°, 135°, 180°, 225°, 270°, 315°)做偏分数阶积分,构造出8个3×3掩模,并把它们叠加后得到如图1所示的5×5掩模。

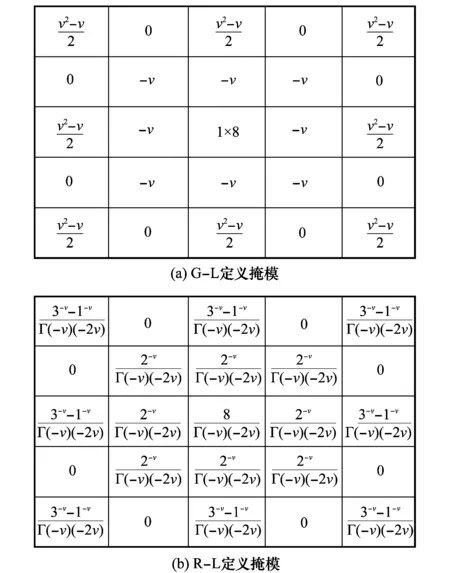
图1　将8个方向偏积分叠加后的掩模

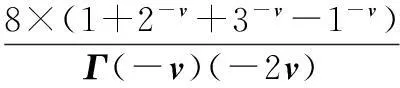
1.3分数阶微积分对信号的作用

已知对于任意平方可积的能量信号s(t)∈L2(R),当v>0时,Dv表示v阶微分乘性算子;D-v=Iv表示v阶积分乘性算子[11]。分数阶微分的Fourier变换为

(5)

根据分数阶算子理论,分数阶微分和分数阶积分互为逆运算,D-=I表示分数阶积分算子,设v′=-v,那么由式(5)可以得到分数阶积分的Fourier变换:

(6)

由式(5)和式(6)画出各阶次分数阶微分和积分的频率响应图。

由图2(a)可知,分数阶微分运算对信号的高频部分具有增强作用,并且随着分数阶微分阶次和频率的增加,增强的幅度呈非线性急速增长。同时分数阶微分对信号的低频部分进行了一定程度的非线性的保留。由图2(b)可知,分数阶积分运算对信号的高频部分具有衰减作用,并且随着分数阶积分阶次和频率的增加,衰减幅度逐渐增长。同时分数阶积分对信号的低频部分进行了较大程度的增强。因此,分数阶微分对图像边缘和纹理有一定的增强和保留作用,而分数阶积分对图像有一定的去噪作用。

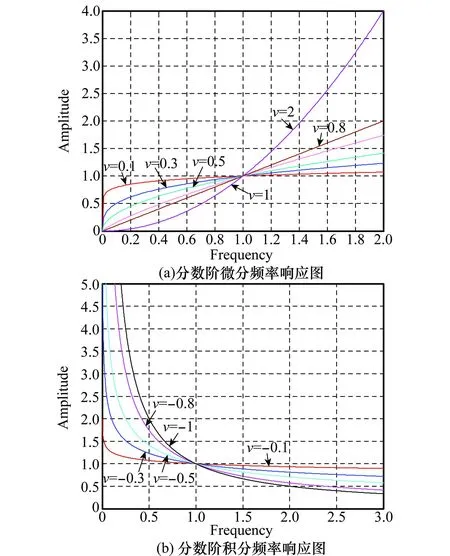
图2　各阶次分数阶微积分频率响应图

2基于分数阶微积分的图像去噪与增强算法

2.1全局自适应分数阶积分图像去噪算法

对于一幅含噪图像而言,其中存在着各种强度的噪声,如果只采用同一的分数阶积分阶次来处理噪声,难以达到较好的去噪效果。所以本文提出一种全局自适应分数阶积分图像去噪算法,该算法对每一个像素点都进行了不同阶次的分数阶积分运算。设图像f(i,j)中每一个像素点8个方向上的梯度幅值的平均值为M(i,j),并进行归一化,从而求出与该像素点对应的积分阶次。取M(i,j)的最大值为Y,最小值为X,将像素点的梯度幅值进行归一化后,可以求出动态的分数阶积分阶次:

(7)

从而可以实现,在梯度均值较大处(看做噪声点)具有较小的负阶次,该阶次的分数阶积分对噪声具有较大的衰减作用;对于梯度幅值中等和较小处(看做图像纹理点)具有相应大小的积分阶次,对图像纹理具有一定的增强和保留作用。将式(7)求出的积分阶次代入图1中的掩模模板,然后再与噪声图像进行卷积运算,就可以实现全局自适应分数阶积分算法对整幅图像的处理。对几类常见的噪声图像如高斯噪声、泊松噪声、乘性噪声和椒盐噪声图像进行仿真实验,去噪效果如第3.1节所示。

2.2基于小概率策略的自适应分数阶微积分去噪与增强算法

将全局自适应分数阶积分图像去噪算法进行仿真实验后,发现该算法相较于文献[16-17]方法的整体图像去噪效果更好,特别是针对于椒盐噪声图像的去噪效果最好。所以本文在全局自适应去噪算法的基础上,进一步提出一种基于小概率策略的自适应分数阶微积分算法(只针对于一类较低强度的椒盐噪声图像),该算法能够在利用自适应分数阶积分去除噪声的同时,利用分数阶微分来增强和保留图像的纹理,从而能够使整幅图像更加清晰。

2.2.1自适应分数阶微积分函数

根据分数阶G-L定义,当分数阶的阶次是负数时为积分运算,当分数阶的阶次是正数时为微分运算,同时依据分数阶的阶次可以连续变化的特点,制定了相应的自适应分数阶微积分阶次的函数,在图像的噪声处具有负阶次,在图像的边缘处具有较大的正阶次,在图像的弱纹理和平滑区域具有较小正阶次。由图2(b)可看出当分数阶积分阶次-1≤vnoise≤-0.5时对高频的图像噪声有较好的衰减效果,根据这些特性,设计自适应阶次v的函数如下:

(8)

上述函数中,t是由小概率策略求取的噪声的梯度阈值,v是每一个像素点对应的分数阶阶次。分割出的每个噪声点的平均梯度为Mnoise(i,j),设Mnoise(i,j)中的最小值为噪声点的最优阈值t=Xnoise,最大值为Ynoise。

对于分割出的噪声点,当分数阶积分阶次为-1≤vnoise≤-0.5时,可以达到较好的去噪效果。同时通过式(8)使不同强度噪声点对应不同的积分阶次,就可以实现强噪声处具有较小的负阶次(负值),较弱噪声处有较大的负阶次,从而获得更好的去噪效果。

当像素点的平均梯度幅值M(i,j)小于噪声阈值t时,该像素点被认为是图像纹理处,对该像素点进行相应正阶次的分数阶微分处理可以达到增强图像纹理的效果。对纹理点的平均梯度进行归一化处理,可以得到不同强度的纹理点对应的微分阶次vtexture=(M(i,j)-2)/(t-2)。从而实现在图像边缘处具有较大的分数阶微分阶次(正值);在图像弱纹理处具有较小的微分阶次;在梯度基本不变化的区域微分阶次为0。根据人眼的视觉特性,取梯度基本不变化的门限值为2,此时人们在视觉上会觉得图像基本无变化。

2.2.2基于小概率策略求取噪声的梯度阈值t

针对较低强度的椒盐噪声图像而言,可以把噪声点的出现看作是一种小概率事件。小概率事件是指发生概率极小的事件[21],一般多采用事件发生的概率在0.01~0.05之间。

一般情况,图像边缘和噪声点的梯度幅值均值都较大,但是边缘像素点大多都是连续的,所以,边缘像素点8个方向上的梯度最小值一般都较小。而噪声点一般都是随机的孤立的点,那么它8个方向上的梯度最小值一般都较大,所以将像素点8个方向上的最小梯度幅值按降序排列,再根据全图噪声概率将椒盐噪声点分割出来。现定义噪声点的出现为随机事件x,那么x发生的概率为Pnoise,设图像f(i,j)的分辨率为A×B,则图像中噪声点数量的期望值为

(9)

将像素点8个方向的梯度最小值Mmin(i,j)按降序排列为H(k),那么当k∈[1,E]时,对应的f(i,j)为噪声点,即满足式(10)的像素f(i,j)为噪声点。

(10)

此时,求取分割出的噪声点的平均梯度Mnoise(i,j),以Mnoise(i,j)的最小值为噪声点的最优阈值t=Xnoise,那么当Mnoise(i,j)越大时候,噪声点越强,对应的积分阶次越小(负值),对噪声的衰减幅度也越大,自适应去噪效果越好。

为了验证小概率策略针对于椒盐噪声图像的有效性,取0.03强度的椒盐噪声为例,去噪效果如图3所示。

原噪声图3(a1)、图3(b1)、图3(c1)的PSNR为20.363 8、19.709 4、20.136 5,那么由图3和表1可以看出对于较低强度的椒盐噪声图像,基于小概率策略的自适应分数阶去噪算法可以达到较好的图像去噪效果。选取总体效果较好的0.03概率作为该算法的概率参数。

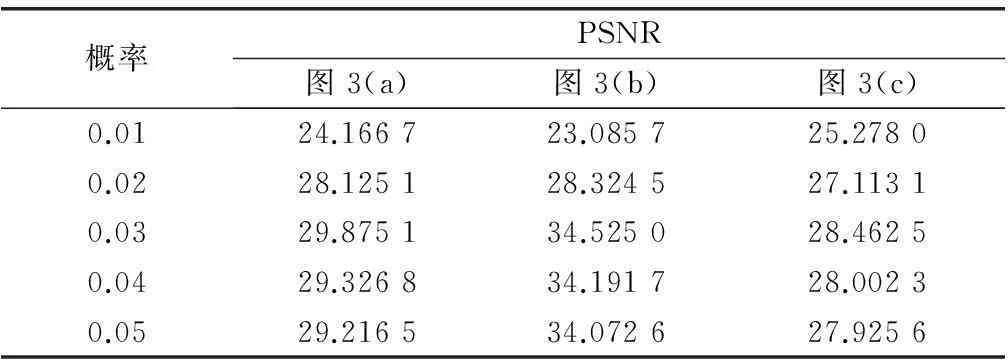
表1　基于小概率策略图像去噪后图像的PSNR

图3　小概率去噪后的图像

3实验与分析

3.1基于全局自适应分数阶积分的图像去噪算法的实验与分析

将本文首先提出的全局自适应分数阶积分去噪算法与文献[16-17]方法进行图像去噪效果的比较实验,同时加入均值滤波、高斯低通滤波、中值滤波、维纳滤波去噪算法。以图4和图5中的原图为对象,加入的噪声分别以均值为0、方差为0.01的高斯噪声、泊松噪声、强度为0.04乘性噪声和强度为0.03的椒盐噪声为例,图像的分辨率均为256×256。其中文献[16-17]中使用的是指定阶次的分数阶积分算法,以取0.5阶次为例。实验结果如图4、图5和表2、表3所示。

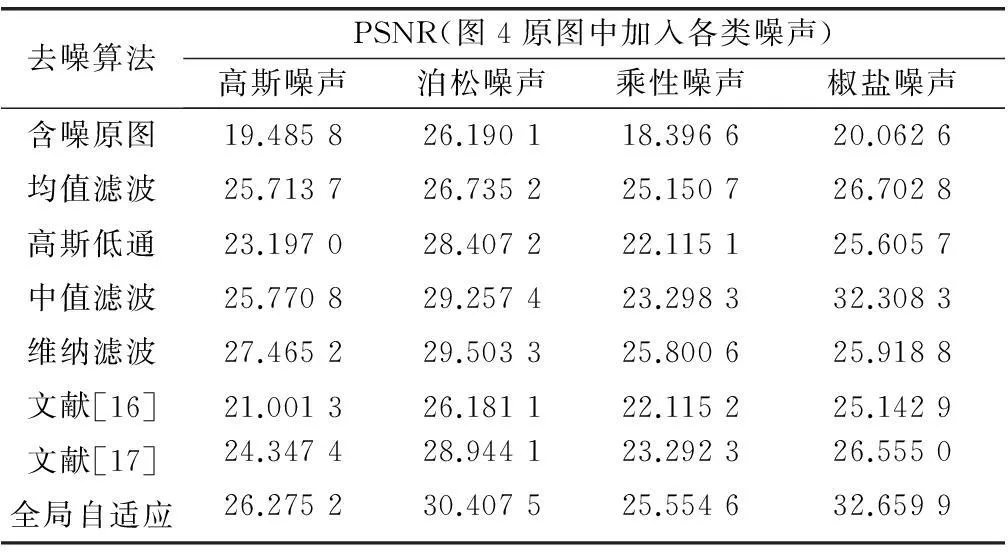
表2　图4中各噪声图像经算法处理后的PSNR

图4　各个去噪算法处理后的图像(1)

图5　各个去噪算法处理后的图像(2)

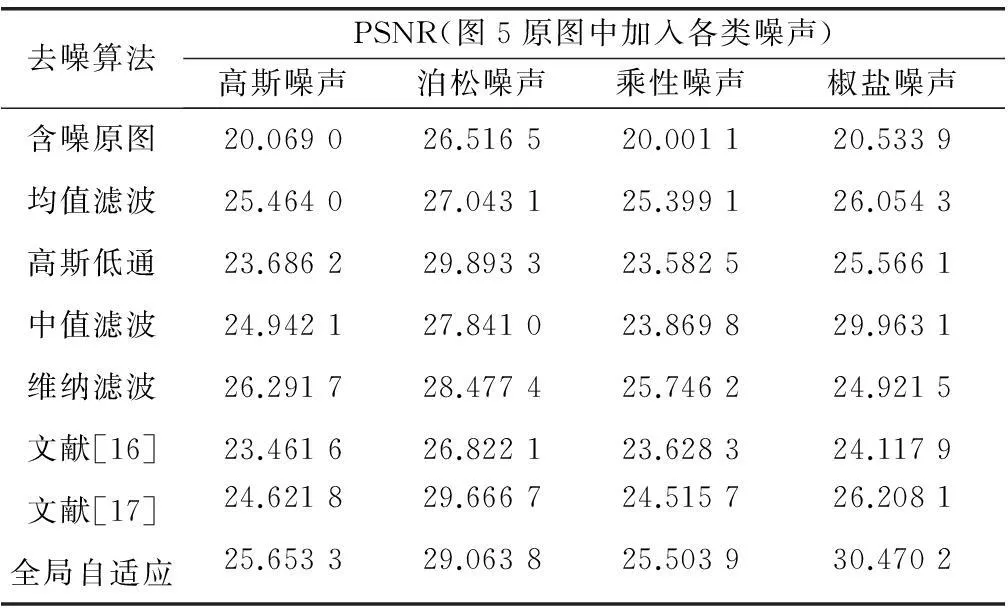
去噪算法PSNR(图5原图中加入各类噪声)高斯噪声泊松噪声乘性噪声椒盐噪声含噪原图20.069026.516520.001120.5339均值滤波25.464027.043125.399126.0543高斯低通23.686229.893323.582525.5661中值滤波24.942127.841023.869829.9631维纳滤波26.291728.477425.746224.9215文献[16]23.461626.822123.628324.1179文献[17]24.621829.666724.515726.2081全局自适应25.653329.063825.503930.4702

由图4、图5和表2、表3可以看出去噪算法对图像都有一定的去噪效果。Wiener维纳滤波根据局部方差来调整滤波器效果,所以对于去除高斯噪声和乘性噪声效果较为明显。中值滤波对于去除椒盐噪声效果较好。文献[16-17]分别采用R-L定义和G-L定义的分数阶积分去噪算法,并对整幅图像都采用的同一的积分阶次,对这几类基于分数阶积分的去噪方法之间进行比较可以发现,本文和文献[17]的算法相比于文献[16]有较好的图像去噪效果,从表2、表3可以看出以本文的去噪算法比较其他方法具有更高的峰值信噪比,其中针对于椒盐噪声图像的去噪效果最佳。

3.2基于小概率策略的自适应分数阶的图像去噪与增强算法的实验与分析

本文进一步提出的基于小概率策略的自适应分数阶算法只针对一类较低强度的椒盐噪声图像,该算法将分数阶积分与分数阶微分同时用于处理同一幅图像,所以该算法可以使图像中的椒盐噪声被去除的同时,图像的纹理也得到较大程度的增强。以强度为0.03的椒盐噪声图像为例,将该算法与维纳滤波、中值滤波、文献[16-17]方法进行图像去噪与增强效果的比较实验。

图6　各个去噪算法处理后的图像(3)

图7　各个去噪算法处理后的图像(4)

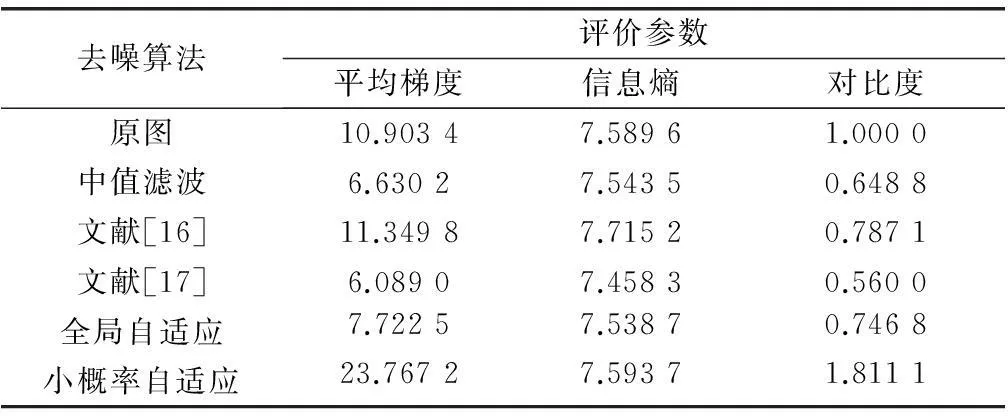
去噪算法评价参数平均梯度信息熵对比度原图10.90347.58961.0000中值滤波6.63027.54350.6488文献[16]11.34987.71520.7871文献[17]6.08907.45830.5600全局自适应7.72257.53870.7468小概率自适应23.76727.59371.8111

表5　图7中各图像的评价参数

图8　本文方法与其他方法的差分图像

首先,对图像直接观察来进行主观评价,由图6、图7可以发现,中值滤波和全局自适应去噪算法对椒盐噪声都具有较好的去噪效果,但是和原图比较,图像的边缘和纹理被弱化,视觉上较模糊。这是由于分数阶积分对图像高频部分具有一定的衰减作用。如图6(h)和图7(h)所示,经过基于小概率策略的自适应分数阶算法处理后的图像虽然还存在零星的噪声点,但是滤除了大部分的图像噪声,并且明显增强了图像的边缘和纹理,使图像更加清晰,视觉效果更好。

如图8所示,将图6(h)和图7(h)分别与原图、中值滤波图、全局自适应去噪图做差分运算,以比较本文算法对图像边缘的增强效果。图8中的图像边缘的轮廓清晰可见,从而说明基于小概率的自适应分数阶算法在去除噪声的同时,能较准确地增强图像的边缘信息,达到较好的图像增强效果。

其次,通过图像数据分析来进行客观评价,通过去噪后图像的平均梯度、信息熵和对比度来比较去噪算法对图像边缘的增强和图像弱纹理的保留能力。其中,对比度的定义为Co=Cprocessed/Coriginal,在图像中以3×3为单位求取对比度,C为所有3×3单位对比度的均值。Coriginal和Cprocessed分别代表原始和增强后图像的对比度。

经过对表格的数据分析可以发现:平均梯度可以表示图像纹理被增强的程度,由表4和表5可以看出,经过基于小概率策略的自适应分数阶算法处理后的图像的平均梯度明显提高,图像边缘和纹理信息被加强。通过对比表格中的信息熵数据,可以看出各去噪算法处理后的图像与原图的信息熵都比较接近,说明上述算法在图像去除噪声的过程中都保留了一定的纹理信息。对比度表征图像的清晰度,对比度过小,整个图像就会是灰蒙蒙的,从表4和表5中可以看出,除了基于小概率策略的自适应算法提高了图像对比度,其他算法的对比度相对于原图都有所降低,所以在视觉效果上本文的去噪算法更佳。因此,基于小概率策略的自适应分数阶算法在去除椒盐噪声、增强图像边缘、保留纹理细节、提高图像对比度等方面具有较好的性能,比较其他方法可以达到更好的图像增强效果。

4结论

基于分数阶的图像去噪是一个新的发展方向,本文提出的全局自适应分数阶积分能在去除噪声的同时保留一定图像纹理信息,但是会使边缘弱化,图像视觉模糊。所以,在全局自适应分数阶去噪算法的基础上，本文进一步提出了一种基于小概率策略的分数阶算法,该算法只针对一类强度较低的椒盐噪声图像。对于一整幅图像而言,该算法实现了在噪声点处采用分数阶积分算法处理,在纹理处采用分数阶微分算法处理,使得图像去噪的同时图像纹理也得到了增强,图像更加清晰,视觉效果更好。

参考文献：

[1] Coupeé P, Manjón J V, Robles M. Adaptive multiresolution non-local means filter for three-dimensional magnetic resonance image denoising[J].IETImageProcessing,2012,6(5):558-568.

[2] Ghazel M, Freeman G H, Vrscay E R.Fractal image denoising[J].IEEETrans.onImageProcessing,2003,12(12):1560-1578.

[3] Chinna R B,Madhavi L M.A combination of wavelet and fractal image denoising technique[J].InternationalJournalofElectronicsEngineering, 2010, 2(2): 259-264.

[4] Landi G, Loh P E. An efficient method for nonnegatively constrained total variation based denoising of medical images corrupted by Poisson noise[J].ComputerizedMedicalImagingandGraphics,2012,36(1):38-46.

[5] Yang H X, Wang X S, Xie P H,et al. Infrared image denoising based on improved threshold and inter-scale correlations of wavelet transform[J].ActaAutomaticaSinica, 2011, 37(10): 1167-1174.(杨恢先, 王绪四, 谢鹏鹤,等. 改进阈值与尺度间相关的小波红外图像去噪[J]. 自动化学报, 2011, 37 (10): 1167-1174.)

[6] Oldham K B, Spaier J.Thefractionalcalculus[M]. New York and London: Academic Press,1974.

[7] Kempfle S. Fractional calculus via functional calculus: theory and applications[J].NonlinearDynamics, 2002, 29: 99-127.

[8] Cafagna D. Fractional calculus: a mathematical tool from the Past for present engineers[J].IEEEIndustrialElectronicsMagazine, 2007, 1(2): 35-40.

[9] MartinoDi J M, Flores J L, Ayubi G A, et al. Edge enhancement of color images using a digital micromirror device[J].ScienceAppliedOptics, 2012, 51(16): 3439-3444.

[10] Wang C L, Lan L B, Zhou S B. Adaptive fractional differential and its application to image texture enhancement[J].JournalofChongqingUniversity, 2011, 34(2): 32-37.( 汪成亮,兰利彬,周尚波. 自适应分数阶微分在图像纹理增强中的应用[J].重庆大学学报, 2011, 34(2): 32-37.)

[11] Pu Y F, Zhou J L, Yuan X. Fractional differencial mask: a fractional differential based approach for miltiscale texture enhencent[J].IEEETrans.onImageprocessing,2010,19(2):491-511.

[12] Pu Y F, Wang W X. Image enhancement masks based on fractional differential[J].JactaAutomaticSinica, 2007, 33(11): 1128-1135.( 蒲亦非,王卫星. 数字图像的分数阶微分掩模及其数值运算规则[J].自动化学报, 2007, 33 (11):1128-1135.)

[13] Wang W X, Li W S, Yu X. Fractional akgorithms for rock fracture images[J].TheImagingScienceJournal,2012,60(3):103-111.

[14] Zhang J, Wei Z H, Xiao L, Adaptive fractional-order multi-scale method for image denoising[J].JournalofMathematicalImagingandVision, 2012, 43 (1): 39-49.

[15] Zhang J, Wei Z H, Xiao L. A fast adaptive reweighted residual-feedback iterative algorithm for fractional-order total variation regularized multiplicative noise removal of partly-textured images[J].SignalProcessing, 2014, 98: 381-395.

[16] Hu J R, Pu Y F, Zhou J L. Fractional integral denoising algorithm[J].JournalofUniversityofElectronicScienceandTechnologyofChina,2012,41(5):706-711.(胡金蓉,蒲亦非,周激流.分数阶积分的图像去噪算法[J].电子科技大学学报,2012,41(5):706-711.)

[17] Huang G, Pu Y F, Chen Q L, et al. Research on image denoising based on fractional order integral[J].SystemsEngineeringandElectronics,2011,33(4):926-932.(黄果,蒲亦非,陈庆利,等.基于分数阶积分的图像去噪[J].系统工程与电子技术,2011,33(4):926-932.)

[18] Miller K S, Ross B.Anintroductiontothefractionalcalculusandfractionaldifferentialequations[M]. USA:Wiley, 1993.

[19] Love E R. Fractional derivatives of imaginary order[J].JournaloftheLondonMathematicalSociety, 1971, 3: 241-259.

[20] McBride A C.Fractionalcalculus[M]. New York: Halsted Press, 1986.

[21] Fan C D, Ouyang H L, Zhang Y J. Small probability strategy based otsu thresholding method for image segmentation[J].JournalofElectronics&InformationTechnology,2013,35(9):2081-2087.(范朝冬,欧阳红林,张英杰.基于小概率策略的Otsu图像分割方法[J].电子与信息学报,2013,35(9):2081-2087.)

李博(1982-),男,博士研究生,主要研究方向为图像处理、机器视觉。

E-mail:l.bo15@mail.scut.edu.cn

E-mail:weixie@scut.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150706.1606.004.html

Image enhancement and denoising algorithms based on

adaptive fractional differential and integral

LI Bo, XIE Wei

(AutomationScienceandTechnology,SouthChinaUniversityofTechnology,Guangzhou510640,China)

Abstract:Due to the problem that traditional algorithms would be easy to ignore the texture of the image while image denoising, a new image denoising algorithm based on global adaptive fractional integral is proposed, which preserves image texture information while removes the noises of image. Secondly, the image enhancement and denoising algorithm based on adaptive fractional differential and integral using small probability strategy is proposed for low intensity salt and pepper noise image. The appearance of salt and pepper noise points is regarded as a small probability event, and the adaptive fractional integral algorithm is used to process the image’s noises while the adaptive fractional differential algorithm is used to enhance the texture of the image. Experimental results show that both the two presented methods have good image denoising effect, and the second algorithm has better effect than other methods on enhancing the image edges.

Keywords:fractional calculus; adaptive; image denoising; image enhancement; gradient; order

通讯作者谢巍(1974-),,男,教授,博士,主要研究方向为鲁棒控制、图像处理。

作者简介：

中图分类号：TP 391

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.29

基金项目：国家自然科学基金面上项目(61174098,60673178)资助课题

收稿日期：2014-12-31；修回日期：2015-05-26；网络优先出版日期：2015-07-06。