GMSK+PN信号信噪比估计

石立国, 王竹刚, 熊蔚明

(1. 中国科学院空间科学与应用研究中心, 北京 100190;

2. 中国科学院大学, 北京 100190)



GMSK+PN信号信噪比估计

石立国1,2, 王竹刚1, 熊蔚明1

(1. 中国科学院空间科学与应用研究中心, 北京 100190;

2. 中国科学院大学, 北京 100190)

摘要：针对数传、测距一体化的调制方式高斯最小频移键控复合伪码测距(Gaussian minimum shift keying+pseudo-noise, GMSK+PN)信号的信噪比估计,提出了一种精度较高、复杂度较低的快速算法。该算法采用层状结构分解的方式,将信号分解为若干信号单元,对每一个分解的信号单元进行功率分配计算或信噪比估计,最后快速准确地计算出整个信号的信噪比。信噪比在 1~13 dB之间时,估计误差小于0.5 dB。利用Simulink仿真工具,验证了该算法的有效性。

关键词：高斯最小频移键控; 再生伪码测距; Tausworthe码; 空间数据系统咨询委员会; 信噪比

0引言

分布式卫星系统要实现编队飞行,需要在测定子卫星之间相对位置的同时,还要求有子卫星间的数据交互。测距、通信一体化设计在许多卫星通信系统中都有涉及,例如中国科学院空间科学与应用中心的深空应答机。但其采用的一体化设计方案是时分复用的方式,无法实现同时完成测距和通信两种任务。目前,空间数据系统咨询委员会(consultative committee for space data systems,CCSDS)正在酝酿一种可以同时传输高码率数传信号和测距信号的技术体制。它采用高斯最小频移键控(Gaussian minimum shift keying,GMSK)[1]进行数传信号的传输,采用再生伪码(pseudo-noise, PN)进行测距[2],被称为高斯最小频移键控复合伪码测距(Gaussian minimum shift keying+pseudo-noise,GMSK+PN)调制方式[3],并成为NASA月球任务的备选方案之一[4-7]。文献[8]最早对GMSK+PN调制方式的测距信号副载波实现形式进行了频谱分析,并给出了仿真结果。文献[9]研究了更具一般性的连续相位调制(continuous phase modulation,CPM)下的测距一体化设计调制解调算法。文献[10-11]给出了GMSK+PN和非平衡四相相移键控(unbalanced quaternary phase shift keying,UQPSK)的优缺点和性能差异。文献[12-13]对GMSK+PN无副载波实现形式的相位抖动和同步进行了仿真。GMSK+PN调制方式从信号层面上来看是真正的测距通信一体化,它兼有GMSK和PN测距的优点[14]:旁瓣衰减快、频谱紧凑、带宽效率高、适合饱和功放;测距捕获时间短,硬件实现复杂度低,测距精度相对较高。由于采用同一个链路同时完成数传和测距两个功能,这种调制方式也有相应的缺点:解调算法相对复杂,数传信号和测距信号互为噪声,影响了解调的性能。因此,为了保证数传信号的误码率性能和测距的精度,数传信号采用相干解调的方式。信噪比估计是信道估计的一个重要组成部分,它提供了切换、功率控制和信道分配算法所需的信道质量信息。在解调过程中,许多解调和译码的算法都需要准确的信噪比信息才能达到最优的性能[15-17]。本文根据GMSK+PN信号的特点,提出了一种适用于GMSK+PN信号的信噪比估计算法。

1GMSK+PN调制解调技术

1.1调制技术

基于GMSK+PN的调制体制、能够同时进行数传和测距的系统框图如图1所示。

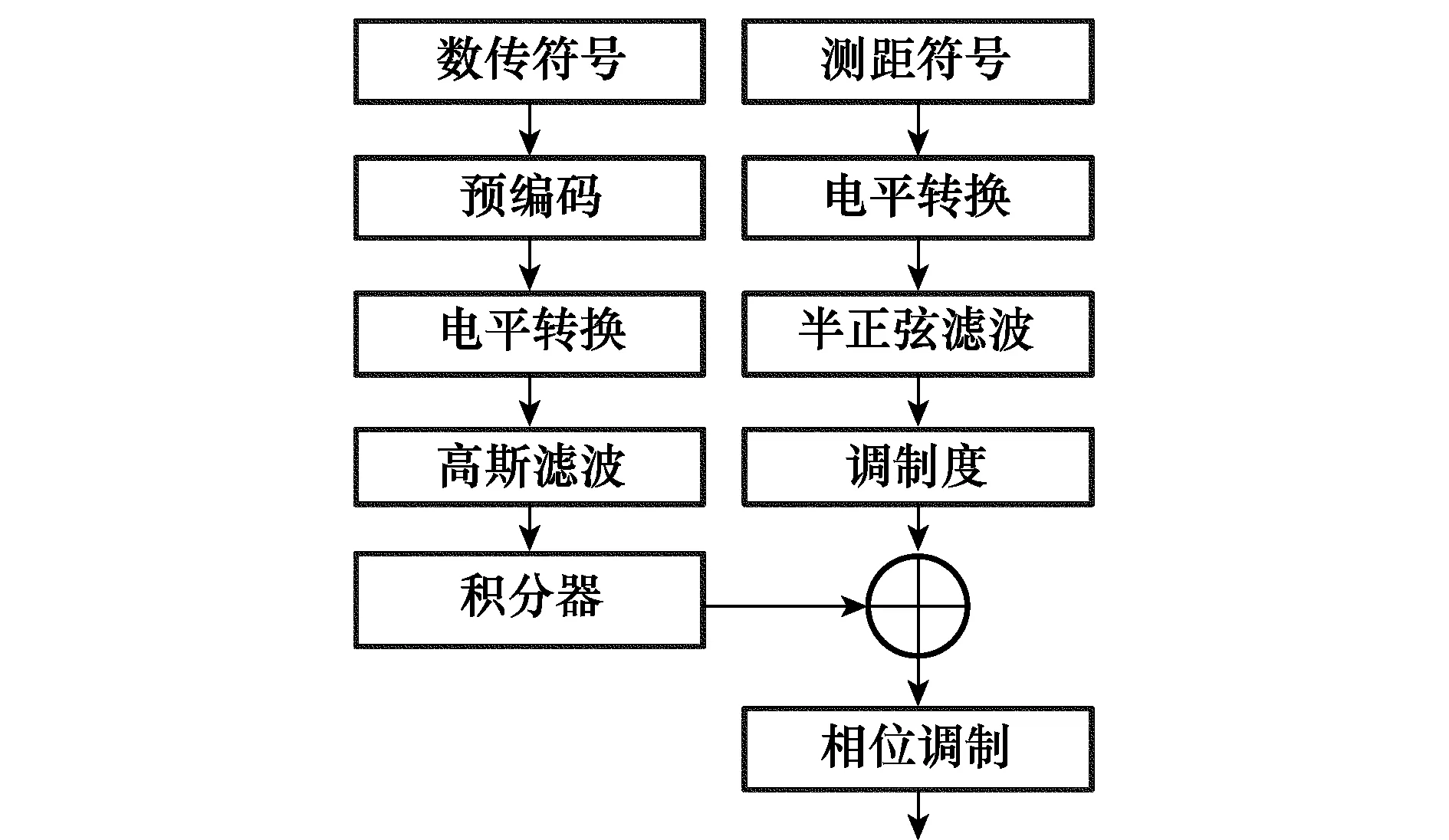
图1　GMSK+PN信号调制框图

测距符号经过电平转换和半正弦滤波后,乘以PN测距调制度(也称测距调制度)得到PN测距信号相位;数传符号经过预编码、电平转换、高斯滤波和积分器后,得到GMSK相位;PN相位和GMSK相位相加后再经过相位调制,即可得到GMSK+PN调制信号

(1)

其中

(2)

式中,Ptot为信号的总功率;ωc为载波角频率;φGMSK(t)为数传信号调制相位;φPN(t)为PN测距信号相位;D(t)为PN序列;md为PN测距调制度;ωPN为PN序列角频率。

1.2解调技术

因为基带的GMSK数传信号(所代表的相位)和PN测距信号(所代表的相位)在时域上是按比例相加的,所以如果得到其中的任何一种信号,就可以由复合信号与某一种“再生”的信号“相减”,得到另一种信号[8]。因为按照常规,GMSK信号在复合信号中所占的能量比例较大。所以,可以直接在已调载波信号上解调,得到GMSK基带信号。再由GMSK基带信号的再调制得到的相位,与输入信号进行复相关,即可得到单独的PN测距信号[18](见图2)。

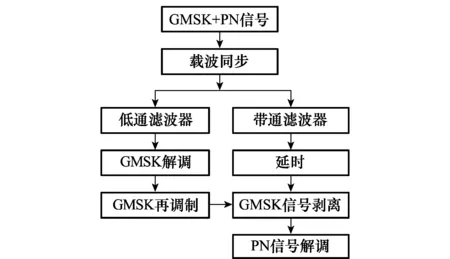
图2　GMSK+PN信号解调框图

2GMSK+PN信号信噪比估计

2.1信号简化波形

由于GMSK+PN信号既包括数传信号,又包括伪码测距信号,无法直接进行信噪比估计。而GMSK+PN信号的结构非常特殊,在数传信号的基础上,直接加入了PN测距信号(作为数传信号的相位抖动存在),故可以采用逐层简化的方式,将GMSK+PN信号分解为若干层,如图3所示。本文采取反推的方法,先估计出PN信号中C1子码分量的信噪比,即可以通过PN信号与C1子码分量的功率分配,得到PN信号的信噪比。进而,通过GMSK+PN信号的能量分配,得到整个GMSK+PN信号的信噪比。

图3　信噪比估计简化模型

在图3中,第1层(最内圈)的面积代表噪声的功率N0,第2层(最内圈和次内圈之间)的面积代表PN测距信号C1子码分量的功率PC1,第3层(次内圈和次外圈之间)的面积代表PN测距信号C2~C6子码分量的功率PC2~C6,第4层(次外层和最外层之间)的面积代表数传GMSK信号的功率PGMSK。PC1/N0可以通过最常用的均值方差比可以求得;当测距PN的码型确定之后,PPN/PC1是确定的;PGMSK/PPN可以通过md来计算。简化模型如图3所示。这种新的信噪比估计算法,可以大大降低GMSK+PN信号的信噪比计算的复杂度。

2.2信噪比估计

2.2.1数传、测距信号能量分配

由贝塞尔函数可知

sin[msin(αt)]=

(3)

cos[msin(αt)]=

(4)

式中,Jk(m)为第一类k阶贝塞尔函数。

GMSK+PN的调制信号表达式如式(1)所示,将式(3)、式(4)代入式(1)并将其展开

(5)

对于数传信号的解调,所用的是式(5)中等号右边的第一项;对于测距信号的解调,所用的是式(5)中等号右边的第2项和第3项。因此,令数传信号功率为PGMSK,PN测距信号的功率为PPN,则有

(6)

式中,md为测距调制度,是GMSK+PN信号中GMSK信号和PN信号能量分配的唯一参数。随md变化,GMSK+PN信号及其数传、测距部分能量的归一化比例的变化趋势如图4所示。

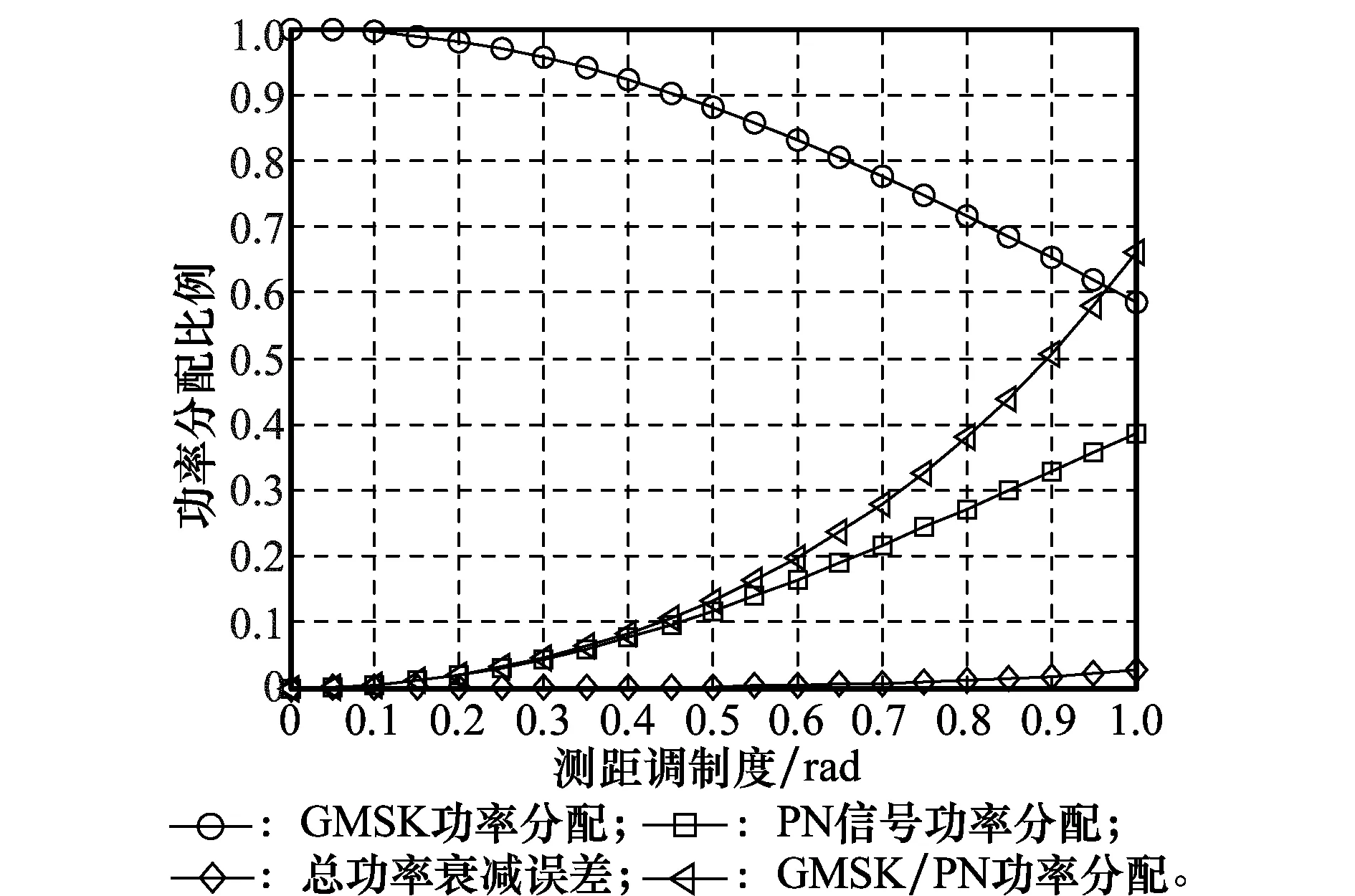
图4　GMSK与PN信号功率分配

当md为确定值时,PGMSK/PPN也是一个固定值。md的值偏低时(小于0.2 rad),则测距部分能量较小,影响测距精度;md的值偏高时(大于0.45 rad),则数传部分能量较小,影响数传解调性能[19-20]。因此,要合理选择md。

由于Bessel函数存在近似,随着md的变化,GMSK信号的总功率Ptot存在不同程度的衰减。所以在求得数传信号功率PGMSK和PN测距信号功率PPN后,需要对GMSK+PN信号总功率Ptot进行修正,如式(7)所示。

(7)

2.2.2PN测距信号功率分配

PN测距信号经过半正弦成型后,与正弦波极其相似,其中C1分量成型后即为正弦波,PN信号成型后波形如图5所示。

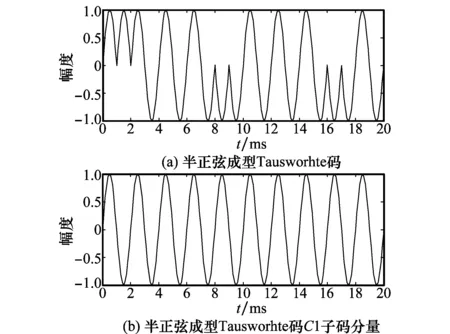
图5　Tausworthe码成型波形

经过整形后的PN与正弦波相比,其功率有部分衰减,如式(8)所示。

(8)

式中,ξ1为Tausworthe码中C1分量与复合码同相的比例,其值随码型变化。可以求得

(9)

对于平衡2倍加权Tausworthe码(weighted-2 balanced Tausworthe,T2B),有

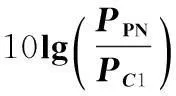
对于平衡4倍加权tausworthe码(weighted-4 balanced Tausworthe,T4B),有

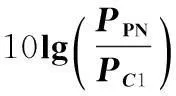
2.2.3单音信号信噪比估计

PN测距信号的C1分量,经过半正弦成型滤波后,即为正弦波,而对这种单载波恒包络的信号的信噪比估计可以使用最简单的均值方差比[21]求得

(10)

式中,a(n)为PN测距信号C1分量瞬时包络。C1分量采样模型如图6所示。其中,ts为采样间隔;tc为测距码片周期;A为实际接收信号的幅度。

图6　PN半正弦成型信号采样量化模型

令A′为信号幅度的估计值,x(k)为每个采样点的幅度,则,经过采样后估计的chip幅度为

(11)

信号功率的估计值S′为

(12)

噪声功率估计值N′为

(13)

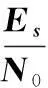
(14)

由第2.2.1节、第2.2.2节和第2.2.3节的结论,可以得到GMSK+PN信号总功率与噪声功率之比为

(15)

3结果分析

通过Simulink搭建仿真模型,取采样率为fs=100 MHz,PN速率为fc=2 MHz,测距调制度md=0.2 rad,再生PN采用T4B,测得信噪比估计值如图7所示。

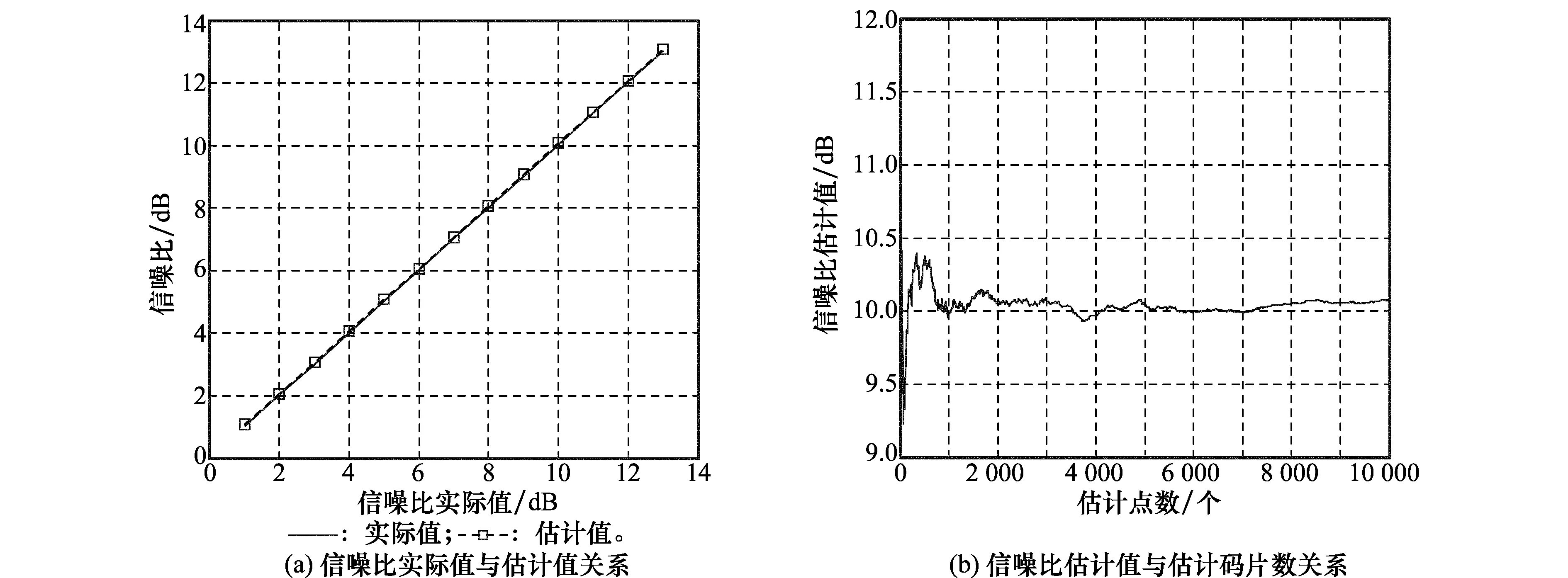
图7　仿真结果

经过仿真可以发现,信噪比估计值与实际值非常吻合,误差在0.5 dB以下。参与计算的码片数在大于1 000时,信噪比估计值基本稳定实际值附近。

4结论

本文给出了在加性高斯白噪声信道中基带GMSK+PN信号的信号模型,同时给出了在此模型下的简单、快捷的信噪比算法。并通过Simulink对该算法进行了仿真。该算法精确度较高,计算复杂度低,且参与计算的码片数目较少,具有工程的可实现性。

参考文献：

[1] CCSDS Recommended Standard 413.0-G-2. Bandwidth-efficient modulations: summary of definition, implementation, and performance [S]. Washington, DC: Consultative Committee for Space Data Systems, 2009.

[2] CCSDS Recommended Standard 414.0-G-2. Pseudo-noise (PN) ranging systems[S].Washington,DC:Consultative Committee for Space Data Systems,2014.

[3] Vassallo E, Visintin M. Analysis of GMSK for simultaneous transmission of ranging and telemetry[C]∥Proc.oftheCCSDSFallTechnicalMeeting, 2009: SLS-RFM_09-08.

[4] Stocklin F, Israel D, Deutsch L, et al. Evaluation of multiple access techniques for simultaneous space communications and tracking[C]∥Proc.oftheIEEEAerospaceConference,2008:1-30.

[5] Deutsch L, Stocklin F, Rush J. Modulation and coding for NASA’s new space communications architecture[C]∥Proc.oftheAIAAInternationalConferenceonSpaceOperations, 2008: 1-8.

[6] Deutsch L, Noreen G K, Hamkins J, et al. Selecting codes, modulations, multiple access schemes and link protocols for future NASA missions[C]∥Proc.oftheIEEEAerospaceConference, 2008: 1-9.

[7] Deutsch L, Hamkins J, Stocklin F. Multiple access schemes for lunar missions[C]∥Proc.oftheAIAAInternationalConferenceonSpaceOperations, 2010: 1-8.

[8] Orr R S, Divsalar D. Combined GMSK modulation and PN ranging for communication and navigation[C]∥Proc.oftheIEEEAerospaceConference, 2008: 1-18.

[9] Orr R S, Divsalar D. CPM/PN modulation and ranging for bandwidth-limited multiple access links[C]∥Proc.oftheIEEEAerospaceConference, 2011: 1-27.

[10] Vassallo E, Visintin M. Analysis of UQPSK and GMSK/PN for simultaneous transmission of ranging and telemetry: ranging correlator results[C]∥Proc.oftheCCSDSSpringTechnicalMeeting, 2010: SLS-RFM_10-03.

[11] Dennis L. Simulations of GMSK-PN and UQPSK[C]∥Proc.oftheCCSDSSpringTechnicalMeeting,2011:SLS-RFM_11-04.

[12] Sessler G, Vassallo E. Analysis of GMSK/PN modulation: effects of phase jumps and noise[C]∥Proc.oftheCCSDSFallManagementMeeting, 2011: SLS-RFM_11-16.

[13] Vassallo E, Visintin M. Synchronization analysis for GMSK+PN modulation[C]∥Proc.oftheCCSDSSpringTechnicalMeeting, 2011: SLS-RFM_11-01.

[14] Visintin M, Vassallo E. Synchronization analysis for GMSK+PN modulation[C]∥Proc.oftheCCSDSFallTechnicalMeeting, 2013: SLS-FRM_13-12.

[15] Salman T, Badawy A, Elfouly T M, et al. Non-data-aided SNR estimation for QPSK modulation in AWGN channel[C]∥Proc.oftheIEEEWirelessandMobileComputing,NetworkingandCommunications(WiMob), 2014: 611-616.

[16] Bellili F, Methenni A, Affes S. Closed-form CRLBs for SNR estimation from turbo-coded BPSK, MSK-, and square-QAM-modulated signals[J].IEEETrans.onSignalProcessing,2014,62(15):4018-4033.

[17] He P, Li Z, Wang X. A low-complexity SNR estimation algorithm and channel estimation method for OFDM systems[C]∥Proc.oftheInternationalConferenceonIEEEInformationScienceandTechnology, 2014: 698-701.

[18] Shi L, Wang Z, Xiong W. Combined GMSK modulation and PN ranging for satellite telemetry[C]∥Proc.ofthe27thConferenceofSpacecraftTT&CTechnology,2014(A-070):1-10.(石立国,王竹刚,熊蔚明.基于GMSK+PN体制的遥测与测距技术[C]∥中国宇航协会飞行器测控专业委员会第27届飞行器测控学术年会论文集,2014(A-070):1-10.)

[19] CCSDS Recommended Standard 41x.0-G-0. Simultaneous transmission of GMSK telemetry and PN ranging[S].Washington,DC:Consultative Committee for Space Data Systems,2014.

[20] Sessler G, Vassallo E, Calzolari G P, et al. GMSK/PN for high rate telemetry and high accuracy ranging of lagrange and mars missions[C]∥Proc.oftheAIAAInternationalConferenceonSpaceOperations,2014:1-14.

[21] Fan H B, Chen J, Cao Z G. An algorithm of SNR estimation for non-constant envelope signal in the AWGN channel[J].ActaElectronicSinica,2002,30(9):1369-1371.(范海波,陈军,曹志刚.AWGN信道中非恒包络信号的SNR估计方法[J].电子学报,2002,30(9):1369-1371.)

石立国(1984-),男,博士研究生,主要研究方向为数字信号处理、信号检测与估计。

E-mail:shiliguo@nssc.ac.cn

王竹刚(1974-),男,研究员,硕士研究生导师,主要研究方向为射频微波通信、数字信号处理。

E-mail:wangzg@nssc.ac.cn

熊蔚明(1963-),男,研究员,博士研究生导师,主要研究方向为电子、通信、计算机、控制和信号处理相关跨学科研究。

E-mail:xwm@nssc.ac.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150818.1519.016.html

SNR estimation algorithm for GMSK+PN signal

SHI Li-guo1,2, WANG Zhu-gang1, XIONG Wei-ming1

(1.CenterforSpaceScienceandAppliedResearch,ChineseAcademyofSciences,Beijing100190,China;

2.UniversityofChineseAcademyofSciences,Beijing100190,China)

Abstract:Gaussian minimum shift keying+pseudo-noise (GMSK+PN) is a modulation method which achieves simultaneously transmission of GMSK data and PN. For the signal to noise ratio (SNR) estimation of GMSK+PN modulation, a fast algorithm with high accuracy and low complexity is proposed. This algorithm applies layered structure decomposition to decompose signals into a number of units. Each decomposed signal’s power is calculated or SNR is estimated. Then, signal power distribution calculation or SNR estimation is conducted successively for according units. Finally, SNR of the entire signal is calculated quickly and accurately. Estimation error is less than 0.5 dB when SNR is between 1~13 dB. Simulink simulation results verify the effectiveness of the proposed algorithm.

Keywords:Gaussian minimum shift keying (GMSK); regenerative pseudo noise (PN) ranging; Tausworthe code; consultative committee for space data systems (CCSDS); signal to noise ratio (SNR)

作者简介：

中图分类号：TN 911.75

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.05

基金项目：国家高技术研究发展计划(863计划)(Y28021A220)资助课题

收稿日期：2015-02-09；修回日期：2015-07-18；网络优先出版日期：2015-08-18。