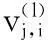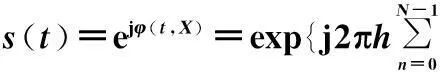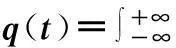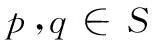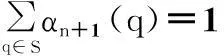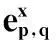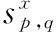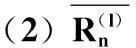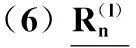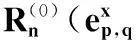卫星通信中低复杂度联合迭代译码算法及仿真

赵宏伟, 张　凯

(1. 西北工业大学电子信息学院, 陕西 西安 710129;

2. 西安烽火电子科技有限责任公司, 陕西 西安 710075)



卫星通信中低复杂度联合迭代译码算法及仿真

赵宏伟1,2, 张凯2

(1. 西北工业大学电子信息学院, 陕西 西安 710129;

2. 西安烽火电子科技有限责任公司, 陕西 西安 710075)

摘要：首先阐述以可靠度作为度量的低密度奇偶校验码(low-density parity check code, LDPC)译码算法,然后提出低复杂度的连续相位调制(continuous phase modulation,CPM)软解调算法,该软解调算法不依赖于噪声方差,避免了信道噪声方差估计不准确对解调性能带来的影响,最后提出一种低复杂度的联合迭代译码算法,该算法以符号/比特的可靠度作为内外译码器之间的迭代信息,具有简单、易于工程实现等优点。仿真结果表明,新的软解调算法的性能与概率域下的解调算法几乎没有差异;在总迭代次数相同的情况下,采用低复杂度联合迭代的性能相比于未采用联合迭代的性能有约0.75 dB的增益。

关键词：连续相位调制; 低密度奇偶校验码; 可靠度信息; 联合迭代译码

0引言

卫星通信是以卫星作为中继的一种通信方式,是在地面微波中继通信和空间电子技术的基础上发展起来的,具有通信距离远、覆盖范围广、不受地面条件约束、建站成本与通信距离无关、灵活机动、能多址连接且通信容量较大等优点。用于卫星通信系统的调制方式与传输信号应具有如下特点:较高的频谱效率、较低的带外功率、信号恒包络特性等[1]。因此,选取适用于卫星通信链路的编码调制方案及相应的解调、译码算法等成为了设计卫星通信系统中关键问题之一。

低密度奇偶校验码(low-density parity-check code, LDPC)码最早由Gallager于1963年在他的博士论文中提出[2],然而由于当时的硬件条件限制,使得LDPC码在提出的30多年里未得到学者的重视。1993年,Turbo码[3]的发现引发了众多学者对LDPC码的研究兴趣。研究发现,当采用和-积译码算法[4-5](sum-product algorithm, SPA)时,其译码性能与Turbo码相似[6-7]。连续相位调制(continuous phase modulation, CPM)作为一种高效的调制技术已成功应用于第二代移动通信当中,如MSK,GMSK。在连续相位调制的信号中,信息被调制在载波相位(或频率)上,信号的瞬时相位由本时刻输入的符号和上一个(或几个)时刻输入的符号共同决定,信号的相位在时间上是连续的,避免了相位的突变。使得CPM信号频谱更为紧凑,带外功率明显小于线性调制的信号。将现代编译码技术与CPM调制技术相结合,能够提高系统的可靠度和频谱利用率,尤其对现役的军用超短波甚高频(very high frequency, VHF)通信及功率受限的卫星通信和深空通信是一个非常有吸引力的技术方案[8],并具有非常重要的意义。

本文各章节内容安排如下,首先介绍卫星通信的特点与应用背景及采用的调制方式与编码类型。第1节以二元LDPC码为例,说明LDPC码的表示方法,对译码需要用到的集合进行了定义,并简要描述了基于靠度的LDPC译码算法。第2节用Trellis对CPM信号进行描述,给出在概率域下的CPM解调算法。在第3节中对信息可靠度进行了定义,给出了可靠度平移准则,基于此提出了基于可靠度的CPM软解调算法,并对算法复杂度进行了分析。第4节里提出低复杂度的联合迭代译码算法,该算法以符号/比特的可靠度作为内外译码器之间的迭代信息,具有简单、易于工程实现等优点。第5节对本文提出的算法进行了性能仿真。第6节总结了全文。

1LDPC码的表示与译码算法

1.1LDPC码的表示

(1) 对于矩阵H中的每一行i,定义

(2) 对于矩阵H中的每一列j,定义

(3) 符号Ni/j表示除了变量节点vj,其余的与校验节点ci相连的所有变量节点;

(4) 符号Mj/i表示除了校验节点ci,其余的与变量节点vj相连的所有校验节点。

1.2基于可靠度的译码算法

LDPC码的译码算法可以分为硬判决译码算法和软判决译码算法。典型的硬判决译码算法有一步大数逻辑译码(one-stepmajority-logicdecoding,OSMLGD) 算法[10-11]和比特翻转(bit-flipping,BF) 算法[12]。软判决译码算法一般是以概率或对数似然比(loglikelihoodratio,LLR)的形式给出,具有较优的译码性能。典型的算法有和-积译码算法和其改进算法,算法的详细描述见文献[2]。然而好的译码性能是以牺牲计算复杂度为代价的。为了降低译码复杂度,同时又不牺牲译码性能,本节给出基于可靠度的译码算法。

在算法中边上传递的信息以及节点处理的信息均采用可靠度来度量。假设经LDPC编码后的码字为C=(c0,c1,…,cj,…,cn-1),采用二进制相移键控(binaryphaseshiftkeying,BPSK)调制方式,经加性高斯白噪声(additivewhiteGaussiannoise,AWGN)信道后接收到rj=(1-2cj)+wj,其中wj为噪声,服从均值0、方差σ2的高斯分布。直观的讲,rj的大小与后验概率p(cj=0|rj)的大小成正比;-rj的大小与后验概率p(cj=1|rj)的大小成正比。因此,可以将rj-(-rj)=2rj作为衡量第j比特的可靠度。

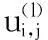
算法 1基于可靠度的LDPC译码算法

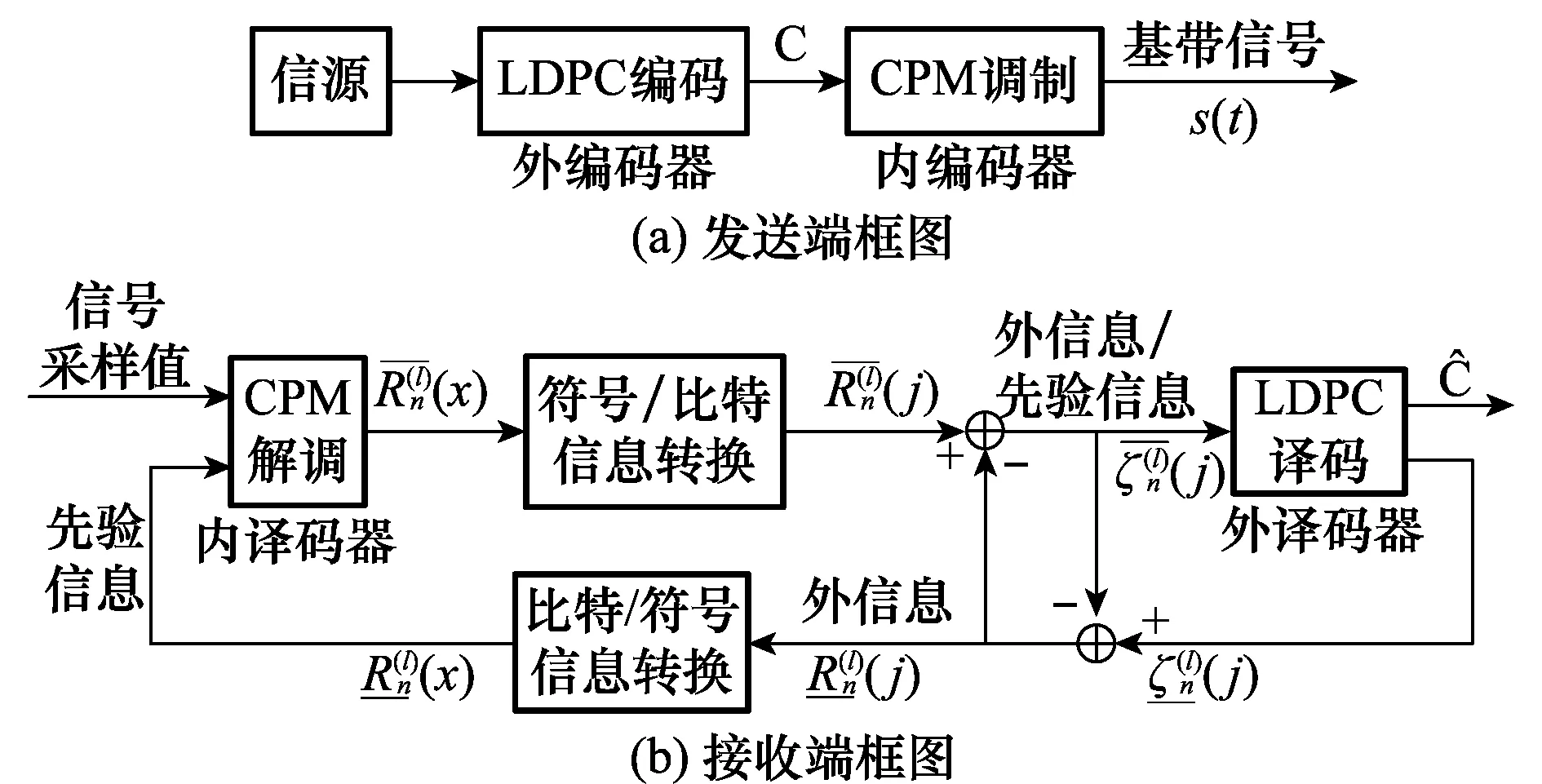
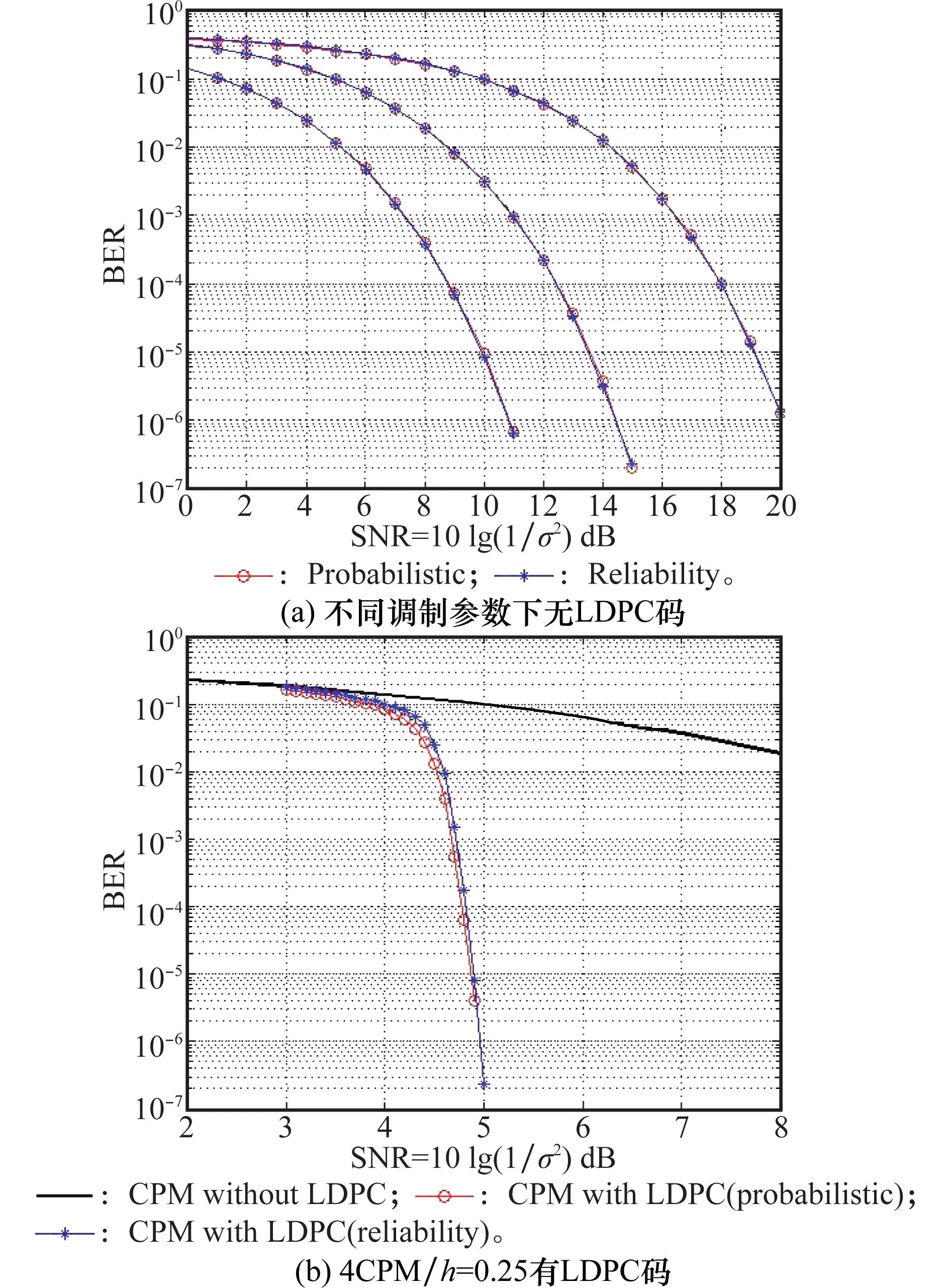
迭代当l

式中,0<ξ≤1为修正因子;

步骤 3判决:对所有的变量节点,计算第l次迭代后的比特可靠度R(l)(j),并进行硬判决

基于可靠度的LDPC译码算法计算复杂度远远低于SPA,算法中仅包含比较和加法运算,非常利于硬件实现。算法中修正因子ξ的选取以及算法复杂度分析详见文献[13]。

2CPM信号调制与解调

2.1信号表达式

CPM信号归一化功率基带复包络数学表达式为

nT≤t≤(n+1)T

L为正整数,表示CPM信号的记忆长度。当L=1时,CPM为全响应CPM;当L≥1时,CPM为部分响应CPM。φ(t,X)表示携带信息的时变相位,h为调制指数,X={X0,X1,…,Xn,…,XN-1}表示长度为N的信息序列,Xn(0≤n

2.2CPM调制

为了简单起见,本文仅考虑L=1时的CPM信号。从编码的角度来看,CPM信号具有记忆效应,当前时刻的相位与本时刻和上一时刻的输入信息相关。因此,可以将CPM的调制过程看作是在Trellis上的编码过程。图2给出了调制指数h=0.5，2CPM时的Trellis。

图2　2CPM，h=0.5时相位变化的Trellis

2.3CPM解调算法

从上述可知,CPM信号是定义在Trellis上的,因此凡是适用于卷积码[14]的译码算法都能够用于CPM解调。类似于卷积码译码,CPM解调可分为硬解调和软解调,硬解调算法采用的信息度量是经量化处理后的判决序列(例如由0、1组成的符号序列)。这类算法的复杂度相当低,如维特比(viterbi)算法[15]。软解调算法(又称BCJR算法或前向后向算法)[16-17]基于概率或LLR,能够与现代纠错码结合,具有最优的解调性能。本节简要回顾并介绍基于概率域的软解调算法,算法的详细描述见文献[18]。

设每段CPM波形采样K点,第n个符号对应的调制信号波形为sn(t),经高斯信道后,接收端采样值为rn(k)=sn(k)+w(k),k=0,1,…,K-1。其中,sn(k)为sn(t)的采样值,w(k)为服从均值0、方差σ2的二维高斯分布的采样值。软解调的过程可分为初始化、前向递归、后向递归、信息提取4部分。

(1) 初始化

第n(0≤n

(1)

式中，符号‖·‖表示欧氏距离。

(2) 前向递归

(3) 后向递归

(4) 信息提取

第n个符号为x的后验概率计算如下：

经过上述4个步骤可以求得关于第n(0≤n

式中,B(j)(x)=b表示二进制序列B(x)中第j位为b的所有符号集合。将比特软信息进行硬判决后得到原输入信息序列的估计。如果p(bj=0)>p(bj=1),则bj=0;反之,bj=1。

从上述对概率域的软解调算法的描述可以看到,算法涉及了大量的指数、乘法和归一化运算,导致这类算法的复杂度非常高。为了降低复杂度,同时又避免解调性能上的损失,经过对BCJR算法中信息度量进行改进,又出现了基于对数的最大后验概率(logmaximumaposteriori,Log-MAP)算法、Max-Log-MAP算法[19]。为了进一步降低算法复杂度,将在下一节给出基于可靠度的低复杂CPM软解调算法。

3低复杂度软解调算法

3.1信息度量的定义

低复杂度软解调算法不再以概率作为衡量符号或比特的度量,而是以概率的对数作为度量。对式(1)求对数得

式中,a0a1是两个与γ独立的参数。那么,对于上式,通过选择合适的a0、a1并进行线性变换后,可得到边的可靠度信息：

(2)

其中

(3)

3.2可靠度平移准则

(3)

3.3基于可靠度的软解调算法

算法 2基于可靠度的软解调算法

前向递归将前向递归变量初始化为α0=(0,-∞,…,-∞),递归计算

同时根据可靠度平移准则对信息向量αn+1进行平移。

后向递归将后向递归变量初始化为βn=(0,0,…,0),递归计算

同时根据可靠度平移准则对信息向量βn进行平移。

信息提取关于第n个符号x的可靠度信息Rn(x)计算如下

4低复杂度的联合迭代译码

4.1系统框图与信息迭代机制

以LDPC码作为前向纠错码的连续相位调制通信系统的发送端框图如图3(a)所示。LDPC编码器将信源产生的0、1比特序列编码得到码字C,而后进行连续相位调制产生基带信号s(t),由于CPM调制是一种定义在Trellis上的编码,因此可以将发送端看作外码为LDPC码与内码为Trellis码的级联。假设信道为AWGN信道,接收端对叠加了噪声的信号进行采样,得到信号采样值。

接收端的框图如图3(b)所示。联合迭代译码的过程是内译码器与外译码器相互传递信息互相迭代的一个过程。

图3　CPM通信系统

首先,内码译码器收到采样值和外译码器两者共同提供的信息进行译码,信号采样值提供的信息称为固有信息(intrinsicinformation),在整个迭代过程中不会改变,外译码器提供的信息称为先验信息(priorinformation),这个信息会随着迭代次数的增加而不断改变。内译码器输出的是关于符号的可靠度信息,需要进行符号/比特信息转换。需要指出的是,在内外译码器的相互迭代过程中,为了确保信息的独立性,内译码器输出的信息需要去除外译码器传递给内译码器的信息,得到的差称为外信息(extrinsicinformation)。

其次,外译码器将内译码器输出的外信息作为自身的先验信息进行译码,外译码器输出的是关于比特的可靠度信息,需要进行比特/符号信息转换。同理为了确保信息的独立性,外译码器输出的信息需要去除内译码器传递给外译码器的先验信息。

这里需要指出的是,在迭代初始时刻外译码器的输入与输出的比特可靠度信息均为0。

4.2符号-比特可靠度转换

从上一小节对信息迭代机制的描述中可以看到,内译码器处理的最小信息单元是符号,而外译码器处理的最小信息单元是比特,当两者之间进行信息传递时需要进行符号可靠度与比特可靠度之间的相互转换。

比特—符号可靠度转换:符号x对应的二进制序列为B(x)=[b0, b1,…,blog2M-1],则符号x的可靠度为

(4)

符号—比特可靠度转换:第n(0≤n

(5)

4.3低复杂度联合迭代译码算法

为了清楚直观地对低复杂度联合迭代译码算法进行描述,用带有下划线的符号表示从外译码器向内译码器方向传递的信息;带有上划线的符号表示由内译码器向外译码器方向传递的信息,上标表示迭代次数。定义如下符号:

(7) J为内译码器与外译码器之间的最大迭代次数。

算法描述如下:

算法 3低复杂度的联合迭代译码算法

(2) 迭代:当l

显然通过对低复杂度的联合迭代译码算法描述可知,算法的性能不但与内译码器(CPM解调模块)和外译码器(LDPC译码模块)的性能紧密相关,而且还受到内外译码器之间的最大迭代次数Jglobal和LDPC译码模块自身的最大迭代次数Jglobal所约束。下一节我们将给出LDPC译码模块在SPA和基于可靠度下两种不同译码算法的仿真性能、CPM解调模块在基于概率域和可靠度下两种不同解调算法的仿真性能,以及不同迭代次数下联合迭代译码的性能比较。

5性能仿真结果

以下所有仿真中所使用的LDPC码均为随机构造[22],码率为0.5、码长10 000。

5.1仿真1

主要针对算法1进行仿真,重点考察的是基于可靠度的LDPC译码算法性能。调制方式选定为BPSK,最大迭代次数设置为50,LDPC码修正因子ξ=0.8。性能仿真结果如图4(a)所示。平均迭代次数如图4(b)所示。为了便于比较,图中同时给出了SPA译码算法下的曲线。

图4　(5 000,10 000)LDPC仿真曲线　　　(最大迭代次数50,修正因子0.8)

从图4中可以看到:

(1) 基于可靠度的译码算法的性能与SPA译码算法的性能基本相同。在误码率为10-6时,两种算法仅有0.04dB的性能差异;

(2) 两种译码算法的迭代次数近乎相同。例如在信噪比为1.7dB(误码率为10-6~10-7)时,SPA算法和基于可靠度译码算法的平均迭代次数分别为13.835和15.431次。

5.2仿真2

主要针对算法2进行仿真,重点考察的是低复杂度软解调算法性能。调制方式选取2CPM/h=0.5，4CPM/h=0.25和8CPM/h=0.125,边的修正因子设置为0.70。仿真结果如图5(a)所示。为了便于比较,图中同时给出了概率域CPM解调算法下的性能曲线。图中曲线从左至右依次为2CPM/h=0.5、4CPM/h=0.25和8CPM/h=0.125。从性能曲线中可以看到,不论CPM调制参数如何选取,基于概率域的解调算法和基于可靠度的解调算法的性能曲线完全一致,没有任何性能上的损耗,而其计算复杂度却大大降低。

为了进一步考察LDPC码在CPM调制通信系统下的性能,对其进行了仿真,调制方式为4CPM/h=0.25。CPM解调算法采用算法2,边的修正因子设置为0.7;LDPC码的译码算法采用算法1,修正因子设置为0.8。仿真结果如图5(b)所示。为了便于比较,图中同时给出了CPM采用概率域下解调、译码采用SPA译码算法下的性能曲线。从曲线中可以看到在适当选取修正因子的情况下,以可靠度作为信息度量的解调/译码算法的性能基本与以概率作为信息度量的解调/译码算法性能相同。例如在误码率BER=10-5时,两种算法间的差异仅有0.02dB,几乎可以忽略。

图5　不同CPM解调算法的性能曲线(CPM边的　修正因子0.70,LDPC码修正因子0.8)

5.3仿真3

(1) 采用联合迭代译码后的性能明显优于未采用联合迭代译码的性能。例如,在误码率BER=10-5时,采用联合迭代译码能够获得约0.75dB的性能增益;

(3) 解调器与译码器之间传递的信息均以可靠度作为度量,不需要对信道的噪声方差进行估计,避免了对噪声方差估计不准确而带来性能上的损失,同时简化了通信系统的结构。

图6　低复杂度联合迭代译码仿真曲线(CPM边的修正因子0.70,LDPC码修正因子0.8)

6结论

本文针对卫星通信系统中采用的CPM调制方式与LDPC编码进行了详细讨论,分别给出了基于可靠度的LDPC译码算法和低复杂度的软解调算法,分析了解调算法的复杂度,并与基于概率域的解调算法进行了比较。在解调与译码算法的基础上,提出了低复杂度的联合迭代译码算法,该算法以符号/比特的可靠度作为内外译码器之间的迭代信息,具有简单、易于工程实现等优点。仿真结果表明,低复杂度的软解调算法在选取适当修正因子的情况下,其性能与概率域下的联合迭代译码算法几乎没有差异。

参考文献：

[1]AulinT,SundbergCE.Continuousphasemodulation-partsIandII[J].IEEE Trans.on Communications,1981,29(3):196-225.

[2]GallagerRG. Low-density parity-check codes[M].Cambridge:MITPress, 1963.

[3]BerrouC,GlavieuxA,ThitimajshimaP.NearShannonlimiterror-correctingcodinganddecoding:turbo-codes[C]∥Proc.of the IEEE International Conference on Communications, Geneva, Switzerland, 1993: 1064-1070.

[4]WibergN,LoeligerHA,KötterR.Codesanditerativedecodingongeneralgraphs[J]. Eoropean Trans.on Telecommunications, 1995, 6: 513-526.

[5]KschischangFR,FreyBJ,LoeligerHA.Factorgraphsandthesum-productalgorithm[J]. IEEE Trans.on Information Theory, 2001, 47(2):498-519.

[6]MacKayDJC,NealRM.NearShannonlimitperformanceoflow-densityparity-checkcodes[J]. Electronic Letters, 1996, 32(18): 1645-1646.

[7]MacKayDJC,WilsonS,DaveyM.ComparisonofconstructionsofirregularGallagercodes[J]. IEEE Trans.on Communications, 1999, 47(10): 1449-1454.

[8]AmatAG,NourCA,DouillardC.Seriallyconcatenatedcontinuousphasemodulationforsatellitecommunications[J].IEEE Trans.on Wireless Communications, 2009, 8(6): 3260-3269.

[9]TannerRM.Arecursiveapproachtolowcomplexitycodes[J]. IEEE Trans.on Information Theory, 1981, 27(5):533-547.

[10]KouY,LinS,FossorierMPC.Low-densityparity-checkcodesbasedonfinitegeometries:adiscoveryandnewresults[J]. IEEE Trans.on Information Theory, 2001, 47(7): 2711-2736.

[11]LinS,CostelloJrDJ. Error control coding: fundamentals and applications[M].2nded.EnglewoodCliffs,NJ:Prentice-Hall, 2004.

[12]GallagerGR.Low-densityparity-checkcodes[J]. IRE Trans.on Information Theory, 1962,IT-8: 21-28.

[13]ChenH,ZhangK,MaX,etal.Comparisonsbetweenreliability-basediterativemin-sumandmajority-logicdecodingalgorithmsforLDPCcodes[J]. IEEE Trans.on Communications, 2010, 59(7): 1766-1771.

[14]EliasP.Codingfornoisychannels[C]∥Proc.of the ZRE Conv.,1955:37-47.

[15]ViterbiAJ.Errorboundsforconvolutionalcodesandanasymptoticallyoptimumdecodingalgorithm[J]. IEEE Trans.on Information Theory, 1967, 13(2): 260-269.

[16]BahlLR,CockeJ,JelinekF,etal.Optimaldecodingoflinearcodesforminimizingsymbolerrorrate[J]. IEEE Trans.on Information Theory, 1974, 20(2): 284-287.

[17]MaX,KavcicA.Pathpartitionsandforward-onlytrellisalgorithms[J].IEEE Trans.on Information Theory,2003,49(1):38-52.

[18]MaX,ZhangK,ChenH,etal.LowcomplexityXEMSalgorithmsfornonbinaryLDPCCodes[J]. IEEE Trans.on Communications, 2012, 60(1): 9-13.

[19]RobertsonP,VillebrunE,HoherP.Acomparisonofoptimalandsub-optimalMAPdecodingalgorithmsoperatinginthelogdomain[C]∥Proc.of the International Conference on Communications(ZCC), 1995:1009-1013.

[20]DeclercqD,FossorierM.DecodingalgorithmsfornonbinaryLDPCcodesoverGF(q)[J]. IEEE Trans.on Information Theory, 2007, 55(4): 633-643.

[21]ChenJ,DholakiaA,EleftheriouE,etal.Reduced-complexitydecodingofLDPCcodes[J]. IEEE Trans.on Communications,2005,53(8):1288-1299.

[22]MacKayDJC.Gooderror-correctingcodesbasedonverysparsematrices[J]. IEEE Trans.on Information Theory,1999,45(2):399-431.

赵宏伟(1980-),男,讲师,博士(后),主要研究方向为卫星通信与导航、自适应信号处理。

E-mail:hongvi_zhao@126.com

张凯(1983-),男,工程师,博士,主要研究方向为无线通信、信号编码。

E-mail:wangshangcaidao@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150910.1050.006.html

Low complexity joint iterative decoding algorithm in satellite

communication and its simulation results

ZHAO Hong-wei1,2, ZHANG Kai2

(1.SchoolofElectronicsandInformation,NorthwesternPloytechnicalUniversity,Xi’an710129,China;

2.Xi’anFengHuoElectronicTechnologyCo.,Ltd.,Xi’an710075,China)

Abstract:A low-density parity check code (LDPC) decoding algorithm which takes the reliability as information metric is firstly described. Secondly, a low complexity soft demodulating algorithm for CPM is proposed. The new demodulating algorithm is independent of variance of noise, which avoids the effect of uncertain estimation of the channel. Finally, a low complexity joint iterative decoding algorithm is proposed, which also takes the symbol/bit reliability as the information metric between inner decoding and outer decoding. The algorithm is simple and easy to apply. Simulation results show that the new demodulating algorithm performs as well as the probabilistic demodulating algorithm; compaing with the decoding algorithm without iterations, the joint iterative decoding algorithm has about 0.75 dB gain, with equal total local iterations.

Keywords:low-density parity check code (LDPC); continuous phase modulation (CPM); reliability information; joint iterative decoding

作者简介：

中图分类号：TN 929

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.24

基金项目：国家自然科学基金(61301094)；中央高校基本科研业务费(3102015ZY040)；山东航天创新基金(2014JJ009)资助课题

收稿日期：2015-05-28；修回日期：2015-07-13；网络优先出版日期：2015-09-10。