姿态稳定控制器择优评价体系构建

殷春武, 侯明善, 李明翔

(西北工业大学自动化学院, 陕西 西安 710129)



姿态稳定控制器择优评价体系构建

殷春武, 侯明善, 李明翔

(西北工业大学自动化学院, 陕西 西安 710129)

摘要：针对航天器总体设计过程中姿态稳定控制器的选择问题,构建了一套基于群决策的姿态控制器择优评价体系,并给出度量评价结果可靠性的可靠度指标。构建了基于控制器鲁棒性、控制力矩、参数敏感性、控制器复杂度和收敛速度的姿态控制器择优评价指标体系,采用同时融合多种赋权法优势的有序加权(ordered weighted averaging, OWA)组合赋权法确定指标权重,给出一种群组专家参与的区间型姿态稳定控制器择优评价方法,并定义了基于区间分析的评价结果可靠度定量描述指标。实例分析了航天器总体设计过程中的姿态稳定控制器择优评价过程,验证了控制器择优评价体系的有效性和评价结果的高可靠度,丰富了决策理论,增强了决策者信心。

关键词：总体设计; 姿态控制; 多属性决策; 区间数; 可靠度

0引言

姿态稳定控制器是保证航天器在轨安全运行和完成航天任务的关键部件,根据航天器及其执行机构的物理特性和运行轨道要求,设计一套鲁棒性强、可靠度高、适应性好的姿态稳定控制器是航天器总体设计过程中所面临并必须解决好一项重要技术。随着控制技术的不断发展,航天器姿态稳定控制器的设计方法和控制策略不断被提出,如何从众多的姿态稳定控制策略中选择一种最合适的控制策略作为航天器姿态稳定控制器是航天器总体设计过程中面临的一个重要问题。因此,建立一套科学、合理的姿态稳定控制策略择优评价体系在航天器总体设计过程中具有重要的实际应用价值。

航天器总体设计中重要分支的姿态稳定控制器设计一直是航天领域的研究热点,航天器姿态稳定控制器的设计随着控制理论的发展不断改进,从最初的经典线性控制方法逐渐发展到以非线性控制为主的先进姿态控制方法。早期的姿态稳定控制是基于小摄动原理对姿态运动学方程线性化,再采用经典线性控制方法设计姿态控制器,对线性化后的航天器姿态动力学方程控制方法,主要有区域极点配置、H2最优控制、H∞鲁棒控制、H2/H∞混合控制、PD控制,文献[1]数值仿真并对比分析了这些经典线性控制方法在姿态控制中的优劣性;随着控制精度要求的提升以及航天器姿态动力学方程本身的非线性,逆控制、反演控制、自适应控制、滑模控制、智能控制等非线性控制方法逐渐被应用到航天器姿态控制中。姿态控制器设计策略的增多导致总体设计过程中控制器选择的盲目性,但关于姿态稳定控制器择优评价方面的研究成果很少。因此,建立一套科学的姿态控制器择优评价机制是现阶段必须解决的问题。

航天器总体设计过程的最优姿态控制策略选择问题其实是一个多属性决策问题。多属性决策主要包含评价指标体系、指标权重确定、评价标度选择和评价方法4部分。多年的理论和实际应用研究,使多属性决策理论和方法成果很丰富,但关于多属性决策结果的可靠性定量描述的研究很少。因此,针对航天器总体设计中的最优姿态稳定控制器择优评价问题,本文将从多属性决策的角度构建一套科学的控制器择优评价体系,并给出评价结果的可靠性定量度量指标,丰富姿态控制器择优评价理论体系,提升决策者的决策信心。

1姿态控制器择优评价指标体系

1.1评价指标体系

评价指标集是航天器姿态控制器择优评价的基础,在设计姿态控制器择优评价指标体系的过程中,应该遵照评价指标体系设计中的明确性原则、可衡量性原则、可接受性原则、实际性原则和时限性原则,结合航天器姿态稳定控制器设计过程中的实际问题来构建姿态稳定控制器择优评价指标体系。利用文献调查法对航天器姿态稳定控制器所要达到的目的进行分析和总结,并结合航天器姿态控制实际需求,确定如下姿态稳定控制器择优评价指标集合:

(1) 系统鲁棒性:闭环系统鲁棒性主要包含对系统参数摄动的鲁棒性和外部干扰的鲁棒性;最初的鲁棒控制器主要用来抵消有界外部环境干扰的影响[2-3],很多经典控制方法均是针对外部环境干扰的鲁棒控制;随后对系统存在有界内部参数摄动的鲁棒控制器设计被重视,具有摄动不变性的滑模控制[4-5]被广泛的应用于解决有界内部参数摄动的鲁棒控制器的设计;随着航天器执行任务复杂度的增加,特别是在轨捕获非合作目标的需要,使得系统内部参数摄动上界未知的航天器姿态稳定控制器设计成为现在的研究热点问题,自适应技术[6-7]和智能逼近技术[8-9]常用来解决内部参数摄动上界未知的航天器姿态稳定控制器设计。

(2) 控制力矩 :主要包含所设计控制器的控制力矩量级大小,控制输入力矩是否满足执行机构的物理需要,控制过程中是否出现抖振现象。最初的姿态稳定控制器设计很少考虑控制力矩的量级大小,以致有的控制输入量级达到104(N·m)[6],完全超出了航天器执行机构提供的能量限制。因此,在执行机构的饱和约束[10]下的姿态稳定控制成为近年来的研究热点。滑模变结构因其摄动不变性和变结构控制的良好性能，近年来被广泛的应用于姿态稳定控制,但其存在的抖振现象使得执行器成为bang-bang控制,不利于执行器物理实现,长期如此还会造成执行器的物理损伤。因此,去抖振[11]成为滑模控制理论研究的一个重要环节。

(3) 参数敏感性:主要是指所设计的控制器中控制参数的多少,以及闭环系统对系统参数变化的敏感性。为了提升姿态控制性能,在控制器设计过程中会增加一些调节参数或控制增益参数,但有些控制器对参数设置很敏感,不恰当的参数设置甚至会导致系统不稳定。因此,控制器设计过程中很大的精力均耗费在选择一组合适的控制参数,经验法和智能算法逐渐被引入到控制器参数寻优求解过程中。

(4) 控制器复杂性:主要是指控制器结构的复杂性,较复杂的控制器,运算步骤多,占用内存大,往往会导致系统控制输入延迟,影响控制性能。同时,在物理电路设计中的节点增多,也会增加故障出现的机率和航天器的负重。

(5) 姿态稳定收敛速度:主要是闭环系统最终稳定的时间长短。在有些航天任务中对航天器的稳定时间有限制[4],要求航天器在有限时间内达到快速稳定,否则可能威胁到航天器的安全运行。因此,姿态稳定控制时间也是一个需要考虑的因素。

1.2评价指标的OWA组合权重确定方法

姿态控制器择优评价指标的重要性各不相同,在控制器择优评价过程中,应该对每个指标的重要性进行区分,即确定出每个指标的权重。指标权重确定方法总体可以分为以经验为主的主观赋权法和以数据分析为主的客观赋权法[11],为综合利用专家经验和客观数据规律,组合赋权法被提出并广泛应用于指标权重确定。控制器择优评价指标权重确定过程中,考虑到各种主、客观赋权法均有自身的优势和不足,本文选择多种指标权重确定方法,利用如定义1所给的有序加权算子对所选指标权重确定方法进行集结,给出一种综合“大多数”指标权重确定方法优势的组合赋权法。

(1)

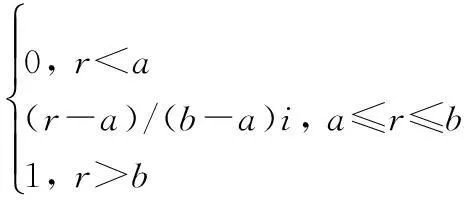
(2)

式中,参数一般设为(a,b)=(0.3,0.8),表示取n个位置中“大多数”位置作为有用位置。

从主观赋权法和客观赋权法中共选择n种指标权重确定方法,设第i种赋权法得到的控制器择优评价指标权重向量为

ωi=(ωi1,ωi2,…,ωi5)T, i=1,2,…,n

(3)

采用OWA算子对n种指标权重集结,得到控制器择优评价指标OWA组合权重向量为

w=(w1,w2,…,w5)T

(4)

2姿态控制器择优评价方法和可靠度分析

(5)

2.1评价信息获取方式和评价方法

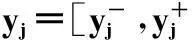
设在航天器总体设计中存在m种姿态控制器设计策略,为选择最优的姿态控制策略应用于航天器姿态稳定控制,数值仿真m种控制器的姿态控制效果,并聘请群组专家根据控制器仿真结果进行评价,记最终评价矩阵为

(6)

综合考虑每个评价指标的重要性,利用加权平均法融合每个姿态控制器的评价信息,其中第i(i=1,2,…,m)个控制器设计策略的指标加权综合评价值为

(7)

为实现区间型加权综合评价值的排序和择优,采用如定义2所给的比较度公式,对m个区间数zi进行两两比较,得到区间数比较矩阵

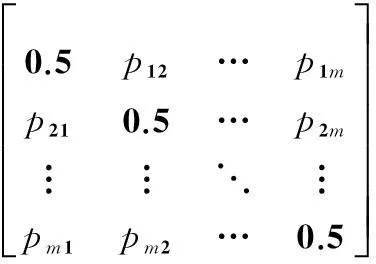
(8)

对比较矩阵P按行取均值,即可得到姿态控制器设计策略择优评价指标[13]为

(9)

择优标准为:δi越大,对应的姿态控制器设计策略越优,选择δi中最大值对应的姿态控制策略作为航天器总体设计中的姿态稳定控制器。

2.2评价结果可靠度指标

现有学者大都集中于决策方法的理论研究,很少关注决策结果的可靠度评价。实际决策过程中,决策方法的选择和最终决策结果是否可用应该被重视。针对本文姿态控制器择优评价结果的可靠性问题,在文献[14]的启发下,给出一种用以度量评价结果可靠度的指标。

(10)

则区间变量[x-,x+]和不确定性参数x可表示为

[x-,x+]=Xc+XdΔ, x=Xc+Xdr

(11)

η=f(x1,x2,…,xn)

(12)

记不确定变量η的均值和偏差分别为ηc,ηd,则有

(13)

(14)

当σ>1时,则认为该评价结果是可靠的。σ比“1”越大,则对应的评价结果越可靠。

(15)

则不确定变量η的均值和偏差分别为

(16)

对存在多个评价结果的可靠性问题,设第i(i=1,2,…,n)个评价结果的可靠度指标为σi(i=1,2,…,n),则总体可靠度指标为

σ*=min{σ1,σ2,…,σn}

(17)

3姿态控制器择优实证分析

考虑外部环境干扰的刚体航天器姿态动力学方程[15]为

(18)

式中,J=JT∈R3×3为转动惯量矩阵;ω∈R3为角速度矢量在体坐标系F下的表示;u∈R3为控制力矩矢量;d∈R3为外部干扰力矩矢量且有界,即‖d‖≤D,这里D为干扰最大值。ω×为矢量ω=[ω1,ω2,ω3]T的反对称矩阵

(19)

(20)

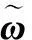
(21)

(22)

(23)

(24)

(25)

(4) 反演滑模控制器

(26)

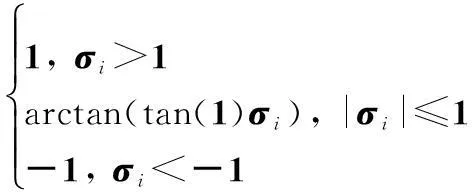
(27)

(5) 适应滑模控制器

(28)　　聘请专家组对这5种姿态控制器进行数值仿真和择优评价,为忽略成本指标和效益指标的区分,采用百分制评价,指标性能越优对应分值越高,使最终评价结果形成效益性指标。对群组专家评价结果统计后得到群组专家对5种控制器的评价结果如表1所示。

不同类型的航天器,对姿态稳定控制器的要求也不一样,导致对姿态稳定控制影响因素的重视程度也各不相同,应该根据实际航天器类型确定评价指标的权重。本文采用5种不同的赋权法确定指标权重向量,计算5种赋权法的位置权重向量为λ=(0, 0.40, 0.50, 0.10, 0)T,利用OWA算子对单一赋权法得到的权重加权组合,具体权重向量如表2所示。

表2　评价指标权重信息

对5种控制器设计策略进行指标加权,得到加权后的综合评价结果为

(29)

利用区间数比较公式计算比较度矩阵为

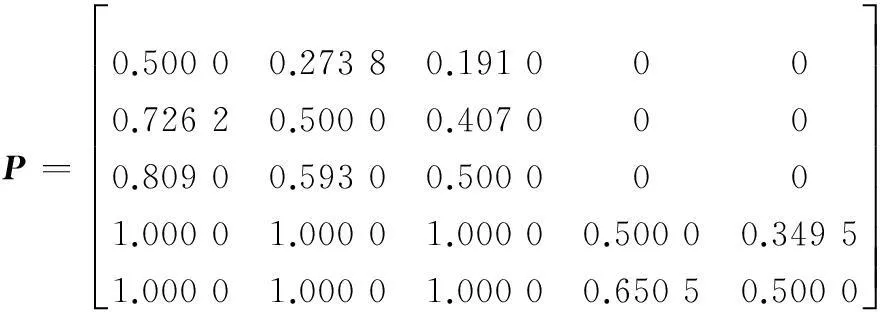
(30)

则最终的排序指标向量为

δ=(0.116 2,0.283 3,0.350 5,0.837 4,0.912 6)T

(31)

通过对排序指标的大小比较,最终选择第5种控制器设计策略作为航天器的姿态稳定控制器设计方案。为了说明该评价结果的可靠度,首先计算每个控制策略的可靠度指标为

σ=(15.202 1,18.073 2,17.634 5,18.685 7,22.737 0)T

(32)

则总体评价结果可靠度为

(33)

式中，σ*≫1,说明本文评价结果的可靠度很高,评价结果可信。通过实际的控制器性能比较也可以看出,第5种控制器设计策略在占据权重比较大的鲁棒性、控制力矩和参数敏感性方面的评价均较其他4种控制策略要优,使得该控制器无论是在参数设计上还是保证系统的鲁棒性方面均有较好的性能。因此,最优控制器是第5种控制器的评价结果是合理的。

4结论

从众多姿态稳定控制策略中选择最优的姿态稳定控制器构成航天器的控制系统,对提升控制器设计速度、延长航天器寿命、保障航天器安全运行并顺利完成航天任务具有重要的意义。本文针对总体设计中缺乏统一的航天器姿态稳定控制器择优评价体系的问题,结合航天器姿态稳定控制目的和航天器实际物理约束,构建了姿态控制器评价指标体系,并基于大多数原则利用有序加权算子集结多种主、客观指标权重,获得姿态控制器评价指标的OWA组合权重,最后给出群组专家参与的姿态控制器择优评价方法,体现了控制器择优过程的公平、公证和客观性。为描述择优评价结果是否可靠,本文给出基于区间分析的定量描述评价结果可靠性的可靠度指标,该指标不仅能有效评价决策方法和结果的可靠度,还能增强决策者的决策信心,丰富了多属性决策的理论研究。通过对总体设计中航天器姿态稳定控制器择优评价实证分析,显示了本文择优评价体系的可行性和科学性。

参考文献：

[1] Won C W. Comparative study of various control methods for attitude control of a LEO satellite1[J].AerospaceScienceandTechnology, 1999(5):323-333.

[2] Yang C D, Sun Y P. Mixed H2/ H∞state-feedback design for microsatellite attitude control[J].ControlEngineeringPractice, 2002 (10): 951-970.

[3] Nagashio T, Kida T, Ohtani T, et al. Design and implementation of robust symmetric attitude controller for ETS-VⅢ spacecraft[J].ControlEngineeringPractice, 2010,18(12):1440-1451.

[4] Lu K, Xia Y. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence[J].Automatica, 2013,49(12): 3591-3599.

[5] Song Z, Li H, Sun K. Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique[J].ISATransactions, 2014,53(1):117-124.

[6] Yeh F K. Sliding-mode adaptive attitude controller design for spacecrafts with thrusters[J].ControlTheory&Applications, 2010,4(7):1254-1264.

[7] Yuan G P, Shi X P, Li L. Adaptive robust attitude maneuvering control for rigid spacecraft[J].SystemsEngineeringandElectronics, 2012,34(12): 2524-2528.( 袁国平, 史小平, 李隆.航天器的自适应鲁棒姿态控制器设计[J].系统工程与电子技术, 2012,34(12): 2524-2528.)

[8] Zou A M, Kumar K D. Adaptive fuzzy fault-tolerant attitude control of spacecraft[J].ControlEngineeringPractice, 2011 (19):10-21.

[9] Kumar K D, Hou Z G .Quaternion-based adaptive output feedback attitude control of spacecraft using Chebyshev neuralnetworks[J].IEEETrans.onNeuralNetworks, 2010,21(9), 1457-1471.

[10] Diego A M, Wolfgang M. Robust control design of a class of nonlinear input-and state-constrained systems[J].AnnualReviewsinControl, 2013 (37) :232-245.

[11] Zhang H X, Fan J S, Meng F, et al. A new double power reaching law for sliding mode control[J].ControlandDecision,2013,28(2): 289-293.(张合新, 范金锁, 孟飞, 等.一种新型滑模控制双幂次趋近律[J].控制与决策,2013,28(2):289-293.)

[12] Yin C W. Fuzzy multiple criteria group decision making method research[D].Xi’an:Xi’an University of Science and Technology, 2007.(殷春武.模糊多准则群决策方法研究[D].西安:西安理工大学,2007.)

[13] Xu Z S. The possibility of interval number sequence method and its application[J].JournalofSystemsEngineering,2003,18(1):67-70.

[14] Guo S X, Lv Z Z, Feng Y S. A non—probabilistic model of structural reliability based on interval analysis[J].ChineseJournalofComputationalMechanics, 2001, 18(1): 56-60.(郭书祥, 吕震宙,冯元生.基于区间分析的结构非概率可靠性模型[J]. 计算力学学报, 2001, 18(1): 56-60.)

[15] Shuster M D. A survey of attitude representations[J].TheJournaloftheAstronauticalSciences, 1993, 41(4):439-517.

[16] Ahmad B Y, Daniele M.Attitude error kinematics[J].JournalofGuidance,ControlandDynamics,2014,37(1):330-335.

[17] Costic B T .Energy management and attitude control for spacecraft[D]. Dissertation:Graduate School of Clemson University, 2001.

[18] Zhong C X,Guo Y,Zhou C,et al. On sliding mode variable structure control andchattering reduction for flexible spacecraft[J].AerospaceControlandApplication,2013,39(2): 24-29(钟晨星, 郭毓, 周川, 等.挠性航天器滑模变结构控制及抖振抑制研究[J]. 空间控制技术与应用, 2013,39(2): 24-29.)

殷春武(1982-),男, 讲师,博士研究生,主要研究方向为航天器姿态控制、决策理论与方法、航迹规划。

E-mail:yincwxa2013@mail.nwpu.edu.cn

侯明善(1959-),男,教授,博士研究生导师,主要研究方向为分析与评估、飞行器导航、制导与控制以及先进控制理论。

E-mail:mingshan@nwpu.edu.cn

李明翔(1987-),男,博士研究生,主要研究方向为航天器姿态控制。

E-mail:limingx2014@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150929.1141.004.html

Construction of attitude stability controller preferential evaluation system

YIN Chun-wu, HOU Ming-shan, LI Ming-xiang

(SchoolofAutomation,NorthwesternPolytechnicalUniversity,Xi’an710129,China)

Abstract:An attitude controller preferential evaluation system based on group decision making is constructed to deal with the controller selection problem in the process of spacecraft overall design, and a reliability index is defined to measure the reliability of the evaluation result. An evaluation index system is constructed, which includes the robustness of controller, controlling torque, sensitivity to parameter, complexity of controller and rate of convergence, determine the weights of indexes with the combination weighting method based on the OWA operator, and an interval group decision making method is provided to select the optimal controller, a quantitative description index of evaluation result’s reliability based on interval analysis is defined. The attitude stability controller preferential evaluation process in the process of spacecraft overall design is analyzed, the effectiveness of the controller preferential evaluation system and the high reliability of the evaluation results are verified, which enriches the theory of decision-making, and enhance the policymakers’ confidence.

Keywords:overall design; attitude control; multi-attribute decision-making; interval number; reliability

作者简介：

中图分类号：V57,N949

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.21

收稿日期：2015-05-11；修回日期：2015-07-13；网络优先出版日期：2015-09-29。