基于关联维数分析的装备技术状态评估

韩小孩, 张耀辉, 王少华, 徐隆洋

(装甲兵工程学院技术保障工程系, 北京 100072)



基于关联维数分析的装备技术状态评估

韩小孩, 张耀辉, 王少华, 徐隆洋

(装甲兵工程学院技术保障工程系, 北京 100072)

摘要：针对传统装备技术状态等级划分方法中存在的不足,提出了基于关联维数分析的装备技术状态等级划分方法。在此基础上,建立了基于径向基神经网络的模式识别模型,对重新划分技术状态等级后的样本数据进行训练,实现了装备技术状态等级模式识别。案例分析表明,该方法可有效改进原有技术状态等级划分不准确的问题,提高技术状态评估的准确性。

关键词：关联维数; 技术状态评估; 径向基神经网络

0引言

技术状态是反映装备实时质量状况的重要指标,其评估工作是实施状态维修的关键内容。装备技术状态评估主要包括技术状态等级划分与技术状态等级模式识别两方面内容。其中,技术状态等级划分主要将装备全寿命过程中的质量状况进行好坏等级划分;技术状态等级模式识别则主要根据已知的装备技术状态监测数据对该装备所处的技术状态等级进行判别。目前针对技术状态评估的研究主要集中在技术状态等级模式识别方面,如文献[1]利用D -S证据理论对多元信息进行融合,实现了装备整体技术状态评估;文献[2-3]将多层模糊技术应用到了技术状态评估中;文献[4]研究了贝叶斯网络在装备状态评估中的应用;文献[5-6]利用隐马尔可夫方法进行了技术状态评估;文献[7]利用层次分析法、德尔菲法进行状态评估;文献[8]将主成分分析法应用于土壤质量评估中。文献[9]建立了4层前向神经网络,有效地判别了轴承的技术状态。然而,针对技术状态等级划分的研究较少,多利用主观经验进行划分,普遍存在技术状态等级划分不准确等问题。与此同时,技术状态等级划分不准确,必然导致技术状态等级识别误差增大,严重影响技术状态评估的准确性。

针对目前装备技术状态等级划分不准确,技术状态评估误差较大的问题。本文主要借鉴分形理论中关联维数计算原理,分析装备技术状态监测数据间的相关性,从而对原有技术状态等级划分结果进行优化。在此基础上,利用已知装备技术状态等级的样本数据计算技术状态监测数据与技术状态等级间的非线性关系,从而实现装备技术状态评估。

1基于关联维数分析的装备技术状态等级划分

1.1理论基础

分形理论认为,现实世界中被分为同一类的事物往往具有一定程度的相似性,并且这一相似性可更广泛地推广到整体与局部之间,即同类事物整体通常具有统一的分形维数[10]。具体地,在处理故障诊断、状态识别问题时,常用关联维数进行分析[11-14]。目前常用的计算关联维数的方法是文献[15-16]提出的G-P算法,其原理如下。

设{Xi}(i=1,2,…,N)为m维相空间中的点集。任取一点Xi={xi1,xi2,…,xim},计算其余N-1个点与Xi的距离。令Cm(r)为关联函数

(1)

式中,r为任取的正数小标量;H(x)为示性函数,满足x>0时,H(x)=1，x≤0时,H(x)=0。

限定r取值范围为[dmin,dmax],其中dmin、dmax分别为吸引子在m维空间中的最小、最大伸展距离。分析Cm(r)性质可知,Cm(r)是一个累积分布函数,可理解为相空间中两点之间距离小于r的分布概率。因此，有Cm(r)=(r/dmax)D(m,r),r∈[dmin,dmax](D(m,r)是与m、r有关的常数)。并且,对于适当范围变动的r1、r2,Cm(r)满足

(2)

式(2)两边取对数得

(3)

由于|r2-r1|足够小时,满足:D2(m,r2)≈D2(m,r1)≈D2(m,r)。因此,式(3)经变换可得

(4)

对于离散数据而言,关联维数D2可近似为lnCm(r)-lnr曲线中线性较好部分的曲线斜率。关联维数D2∈[0,+∞),主要反映数据中主体数据的聚集程度。其取值越小,表明数据越聚集,即数据归类越正确。假设某组数据的lnCm(r)-lnr曲线如图1所示。

图1　某组数据的ln Cm(r)-ln r曲线图

图中d0代表无限接近dmin的数。由图1可知:r∈[d1,d2]时,曲线线性较好,可用于计算该组数据的关联维数。令该组数据全体为集合Ω。当r∈[d0,d1]时,H(r-‖Xi-Xj‖)=1的全部数据为集合A:

当r∈[d1,d2]时,H(r-‖Xi-Xj‖)=1的全部数据为集合B;当r∈[d2,dmax]时,H(r-‖Xi-Xj‖)=1的全部数据为集合C。集合B、C表达式与集合A形式相同。对照图1曲线特征可知,集合B为该组数据的主体数据。令集合D=A-A∩B,E=C-C∩B。则集合D∪E中数据为整体数据中与主体数据不相容的部分,不能反映整体数据的分形特性。

1.2装备技术状态等级划分

装备的劣化过程极易受其所处状态及工作环境影响,可认为是一个动力系统的变化过程。与此同时,由于单个装备技术状态监测数据收集不可重复,收集的装备技术状态监测数据变化过程仅可以反映该装备在其特殊工作环境下的一种技术状态劣化过程,且监测数据无法遍历该装备可能存在的所有技术状态。因此,不能用于评估其他工作环境下的不同装备的技术状态。实际上,装备的技术状态监测数据并无明显的从属性。技术状态监测数据相近的同型号的不同装备,其技术状态通常也相似。因此,可用多台装备的技术状态监测数据构建装备技术状态评估模型。装备技术状态等级划分是其状态评估的必要内容。传统的装备技术状态等级划分,通常依据装备实际劣化规律,通过专家主观经验进行,必然存在等级划分不准确的问题。因此，需要对客观数据进行分析,从而剔除那些技术状态划分不准确的数据。本文通过分析数据间的关联维数,实现装备技术状态等级的准确划分。

首先依据专家主观经验将装备历史监测数据划分为反映技术状态好坏的多个等级。根据多重分形理论,每个等级所对应的数据集合应具有统一的分形维数。取第i、j两个等级进行分析。分别计算两个等级下数据的关联维数,分析分类结果的准确性。由于关联维数分析的实质是分析同类数据间的“贴近程度”,与向量间“距离”本质相同。因此在分析装备技术状态等级关联维数时,可用能表征装备技术状态的参数数目代替相空间维数m。假设,利用上述关联维数计算方法绘制两个等级的lnCm(r)-lnr曲线如图2所示。

图2　第i与j类数据ln Cm(r)-ln r曲线图

如图2(a)所示,对第i个级别的数据进行分析可知:数据多集中在r∈[d1,d2]区间范围内(集合B),该区间内曲线线性特征较好,可用于计算该分类下数据的关联维数,且关联维数主要反映距离在该区间内的数据特征。对于距离在r∈[d0,d1]及r∈[d2,dmax]间的数据(集合A与集合C),需进一步判断其与主体数据之间的关系,从而将不相容的数据(集合D∪E)分给相邻级别进行计算。将保留下来的数据(集合Ω-D∪E),作为第i个级别的基准数据。由于主观分类不一定能完全放映客观数据的聚类规律,因此也存在如图2(b)所示无明显分形特征的图形。此时,可将第j类的数据重新划分到其相邻的类别中,并将划分后的类别重新计算。如此重复直到多数数据成功分类为止。最后,计算各类别中数据的聚类中心,以及各聚类中心间的距离,从而将距离较近的类别归为同类,实现技术状态等级准确划分。

为避免重复工作,此处约定同组数据一旦离开所属类别便不会再次被划分到该类中,且数据的再次划分过程只在相邻类别间发生。具体的计算步骤如下:

步骤 1根据历史经验,给定技术状态等级数目k,并将各技术状态监测数据初步划分到k个等级中。

步骤 2计算各等级内数据的关联维数,将不相容的数据划分到相邻等级。

步骤 3重复步骤2。(其中与各类均不相容的数据,暂不归类)直至多数数据实现归类(由专家确定比例值),设为条件1。

步骤 4若条件1不成立,则应重新给定技术状态等级数目,重复步骤1~步骤3;若条件1成立,则需计算各等级数据集合的聚类中心,进而转入步骤5。

步骤 5设I,J为技术状态监测数据重新归类后,任意第i与j个等级的数据集合。其聚类中心分别为ci,cj。将ci(cj)代入J(I)中,若与之相容,则第i(j)个等级的数据归入第j(i)个等级。若不相容,则保持不变。

步骤 6重复步骤2、步骤3、步骤5,直至不存在步骤5中所述相容的情况。最终将装备技术状态重新划分为l个等级。

实际上,由于收集到的装备技术状态监测数据不可能覆盖装备所有状态,因此上述重新划分后的各等级内的数据仅可反映该等级下的部分特征,不能直接用于评估装备技术状态。应进一步分析装备技术状态监测数据与装备技术状态等级间的非线性关系,从而实现装备技术状态等级模式识别。

2技术状态等级模式识别

模式识别是指利用计算机或其他装置对物体、图像、图形、语言、字形等信息进行自动识别[17]。对已有部分样本数据的装备进行技术状态等级模式识别时,常采用具有良好逼近非线性函数能力的神经网络技术进行研究。其中,BP神经网络是目前应用最为成熟的一种函数逼近方法。然而,该方法存在局部最优解、收敛速度慢等问题,不适合用于评估装备技术状态。本文采用径向基神经网络对技术状态进行模式识别。与BP神经网络不同,径向基神经网络属于局部逼近网络,较之BP神经网络更易获得全局最优解,且收敛速度快,具有很强的函数逼近及模式分类能力[18-19]。

在进行装备技术状态评估时,可建立如图3所示径向基神经网络结构。

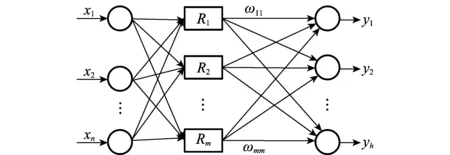
图3　径向基神经网络结构示意图

图中,输入(x1,x2,…,xn)为样本数据,其中各节点分别对应样本数据各参量值;输出(y1,y2,…,yh)为装备技术状态等级。假设装备技术状态共分3个等级(良好、劣化、故障),则网络应有3个输出节点分别代表“良好”、“劣化”、“故障”。网络输出为良好:[1,0,0];劣化:[0,1,0];故障:[0,0,1]。

隐层节点为(R1,R2,…,Rm)。其中,第i个节点的激活函数为

(5)

式中,xp为输入样本的第p个参量值；ci为第i个隐层节点的中心。

神经网络的输出函数为

(6)

式中,权值ωik可用最小二乘法计算。

在进行技术状态等级模式识别时,仅需将监测数据代入已训练好的神经网络,根据网络输出值判定即可。输出值最大的节点所代表的状态即为该监测数据下装备的技术状态,该输出值称之为评估值。

3示例分析

本文选取变速箱油液分析数据,对某型装备的变速箱技术状态进行评估,以验证本文方法的可行性。由于数据来源于多台装备,因此需首先将数据中非变速箱劣化因素(换油等因素)引起的油液质量变化进行处理。具体的处理方法可查阅相关文献,此处不加赘述。共选取油液中铁、铬、铅、铜、铝、硅、钠、镁、钙、钡、磷、锌共12种元素的浓度作为特征参量进行分析。样本容量为59,根据经验划分为“良好”样本18例、“劣化”样本21例、“故障”样本20例。样本数据归一化处理如表1所示。

表1　某型装备变速箱油液中各类元素浓度(ppm)归一化数据

利用上述方法,绘制“良好”等级下的lnCm(r)-lnr曲线，如图4所示。

图4　良好数据ln Cm(r)-ln r曲线图

图中,d1=0.170 9,d2=0.626 3,dmin=0.115 8,dmax=1.554 2。分析可知,样本数据总体为集合Ω,集合内元素为各样本的序号;d1与d2之间的数据为该技术状态等级的主体数据(集合B),并且可用该距离范围内的数据计算分形维数。距离在dmin与d1之间的数据为集合A,d2与dmax之间的数据为集合C。计算得D∪E=(A∪C)-(A∪C)∩B={18}。对照数据表可知序号为18的数据应从“良好”等级中剔除。同理,经多次运算可得重新分类后的样本数据共有49组。其中,“良好”数据17组、“劣化”数据16组、“故障”数据16组。

根据重新分类后的样本数据可构建3层径向基神经网络。该网络共包括3个网络输出点,分别代表3个技术状态等级。其中,“良好”数据输出为[1,0,0];“劣化”数据输出为[0,1,0];“故障”数据输出为[0,0,1]。

分别用约简后的数据及原数据训练神经网络可得网络1、网络2,其训练结果误差收敛趋势,如图5所示。网络1与网络2均可达到训练目标,且前者较之后者训练速度更快。

图5　径向基神经网络训练误差收敛趋势

随机试验样本共10组,其归一化数据如表2所示。将样本数据代入上述两个训练好的神经网络进行计算。可得评估结果如图6所示。其中,网络1输出为:样本1~样本3为良好,样本4~样本7为劣化,样本8~样本10为故障;网络2输出为:样本1~样本3为良好,样本4~样本10为劣化。对比分析可知,网络1的分类正确率为90%;网络2的分类正确率为70%。用约简后数据训练的神经网络明显好于用原始数据直接训练的神经网络。可见,重新划分的技术状态等级明显优于原来的划分结果。

表2　归一化试验样本

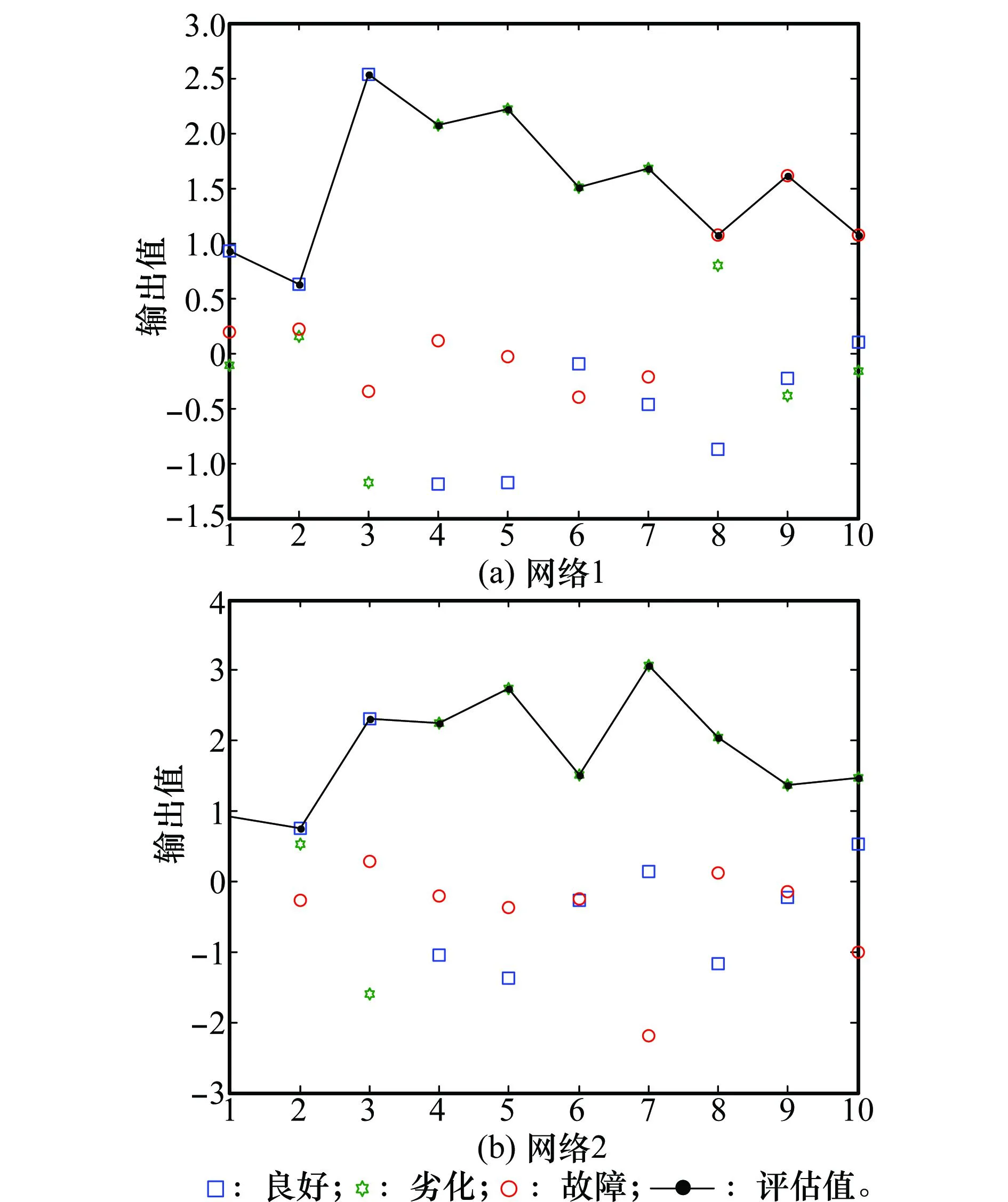
图6　试验样本神经网络输出

4结论

本文利用分形理论中的关联维数分析了同类数据间的相关关系,对装备技术状态等级划分进行了优化。在此基础上利用径向基神经网络实现了装备技术状态等级模式识别。与依据经验划分相比,文中所用方法可明显提高装备技术状态等级划分的准确性,从而使技术状态评估结果更加可信。

参考文献：

[1] Geng J B, Qiu W, Kong X D, et al. Technical condition evaluation for devices based on rough set theory and D -S evidence theory[J].SystemsEngineeringandElectronics,2008,30(1):112-115.(耿俊豹,邱玮,孔祥纯,等.基于粗糙集和D -S证据理论的设备技术状态评估[J].系统工程与电子技术,2008,30(1):112-115.)

[2] Salwa A, William D, Bernard J, et al. Constructing a fuzzy knowledge based system: an application for assessing the financial condition of public schools[J].ExpertSystemwithApplications, 2004, 27: 349-364.

[3] Kei K, Ayaho M. Condition state evaluation of existing reinforced concrete bridges using neuro-fuzzy hybrid system[J].ComputersandStructures, 2003, 81(18/19): 1931-1940.

[4] Zhou Z B, Dong D D, Zhou J L. Application of Bayesian networks in reliability analysis[J].SystemsEngineering-Theory&Practice, 2006, 26(6): 955-100.(周忠宝, 董豆豆, 周经纶. 贝叶斯网络在可靠性分析中的应用[J].系统工程理论与实践, 2006, 26(6): 95-100.)

[5] Bunks C, Mccarthy D, Alani T. Condition based maintenance of machines using hidden Markov models[J].MechanicalSystemsandSignalProcessing, 2000, 14(4): 597-612.

[6] Miao Q, Makis V. Condition monitoring and classification of rotating machinery using wavelets and hidden Markov models[J].MechanicalSystemsandSignalProcessing,2007,21(2):840-855.

[7] Fei X, James D M. Power system risk assessment and control in a multi-objective framework[J].IEEETrans.onPowerSystems, 2009, 24(1): 78-84.

[8] Reid M K, Spencer K L. Use of principle components analysis on estuarine sediment datasets: the effect of data pre-treatment[J].EnvironmentalPollution, 2009, 157(8/9): 2275-2281.

[9] Gao R X, Wang C T. A neural network approach to bearing health assessment[C]∥Proc.oftheInternationalJointConferenceonNeuralNetworksandtheInternationalJointConferenceonNeuralNetworks, 2006: 899-906.

[10] Zhu H, Ji C C.Fractaltheoryanditsapplications[M].Beijing:Science Press,2011.(朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011.)

[11] Yang Y, Wang H H, Yu Z T, et al. A rotor fault diagnosis method based on ITD improved algorithm and correlation dimension[J].JournalofVibrationandShock, 2012, 31(23): 67-70.(杨宇, 王欢欢, 喻镇涛, 等. 基于ITD改进算法和关联维数的转子故障诊断方法[J].振动与冲击, 2012, 31(23): 67-70.)

[12] Alberto R, Maria M. A method for the correlation dimension estimation for on-line condition monitoring of large rotation machinery[J].MechanicalSystemsandSignalProcessing, 2005, 19: 939-954.

[13] Koley C, Purkait P, Chakravorti S. SVM classifier for impulse fault identification in transformers using fractal features[J].IEEETrans.onDielectricsandElectricalInsulation, 2007, 14(6): 1538-1547.

[14] Xiao Y Q, Feng L G. A novel linear ridgelet network approach for analog fault diagnosis using wavelet-based fractal analysis and kernel PSA as preprocessors[J].Measurement,2012,45(3):297-310.

[15] Grassberger P, Procaccia I. Characterization of strange attrac-tors[J].PhysicalReviewLetters,1983,50(5):346-349.

[16] Grassberger P, Procaccia I. Measuring the strangeness of strange attractors[J].PhysicaD:NonlinearPhenomena,1983,9(2):189-208.

[17] Bian Z Q, Zhang X G.Patternrecognition[M].2nd ed.Beijing:Tsinghua University Press,2000.(边肇祺,张学工.模式识别[M].第2版.北京:清华大学出版社, 2000.)

[18] Martin T H, Howard B D, Mark B.Neuralnetworkdesign[M].America: PWS Publishing Company, 2002: 197-222.

[19] Catelani M, Port A. Fault diagnosis of electronic analog circuits using a radial basis function network classifier[J].Measurement, 2000, 28(3): 147-158.

韩小孩(1987-),男,博士研究生,主要研究方向为装备维修理论与技术。

E-mail:hanleiacd@163.com

张耀辉(1960-),男,教授,主要研究方向为装备维修理论与技术。

E-mail:zyh532@sohu.com

王少华(1986-),男,博士研究生,主要研究方向为装备维修理论与技术。

E-mail:aafe77330@163.com

徐隆洋(1978-),男,讲师,主要研究方向为装备战场抢修。

E-mail:hanlei@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150831.1754.010.html

Equipment’s condition evaluation based on the analysis of

correlation dimension

HAN Xiao-hai, ZHANG Yao-hui, WANG Shao-hua, XU Long-yang

(DepartmentofTechnologySupportEngineering,AcademyofArmoredForceEngineering,Beijing100072,China)

Abstract:In order to solve problems in the grade classification of equipment’ condition with the traditional ways, the method based on the analysis of correlation dimension is proposed. And on that basis, we built the radial basis function (RBF) neural network and trained it by sample data which we got previously. Then the grade of verification samples is identified by the net. As shown in the case, the proposed method can effectively mitigate the problem in the equipment’s condition evaluation.

Keywords:correlation dimension; condition evaluation; radial basis function (RBF) neural network

作者简介：

中图分类号：E 92

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.18

基金项目：军队科研计划项目资助课题

收稿日期：2015-02-09；修回日期：2015-05-14；网络优先出版日期：2015-08-31。