基于改进对称量测方程的多目标跟踪

吴　潇, 黄树彩, 凌　强, 钟　宇

(空军工程大学防空反导学院, 陕西 西安 710051)



基于改进对称量测方程的多目标跟踪

吴潇, 黄树彩, 凌强, 钟宇

(空军工程大学防空反导学院, 陕西 西安 710051)

摘要：采用传统对称量测方程对多维多目标跟踪会增加伪观测量,在目标航迹交叉点附近容易产生较大跟踪误差。针对这一问题,提出一种基于多项式因式分解思想的改进对称量测方程,通过建立同一目标在不同坐标系中状态之间的联系,将新量测集与原始量测集的对应关系描述的更加准确,利用泰勒展开公式推导出新量测的观测误差,求出相应的观测误差协方差阵。与现有对称量测方程方法和联合概率数据关联算法仿真对比,验证所提方法不仅延续了对称量测方程时效性优势,而且提高了目标在航迹交叉时的跟踪精度。

关键词：对称量测方程; 多目标跟踪; 多项式因式分解

0引言

与单目标跟踪相比,多目标跟踪不仅面临更加复杂的噪声背景,而且还要处理好量测-航迹关联。传统多目标跟踪算法[1]以数据关联为核心,要先进行关联运算,然后再对多个目标独立跟踪,如联合概率数据关联算法(joint probability data association,JPDA)、多假设跟踪算法(multiple hypothesis tracking,MHT)等,这些方法随着目标数目增多计算量会剧增,极大地制约了算法的时效性。

20世纪90年代,Kamen[2]首创了一种基于对称量测方程(symmetric measurement equation,SME)的多目标跟踪方法,通过构造原始观测值的对称函数得到一组新量测,可以同时估计多个目标的状态,而不需要数据关联运算。起初,Kamen仅考虑了一维空间量测数目与目标真实数目相等的情况,并且构造的新量测也只有乘积和形式[2-3],随着研究的深入,不仅将SME的适用范围推广到多维空间,以及存在虚警、漏警的情况[4],而且构造了幂次和形式的SME[5]。

在处理多维多目标跟踪问题时,Kamen做法[5]是各维独立进行SME跟踪,Muder[6]指出该处理方法会增加伪观测量,在航迹交叉时容易产生较大影响。Lee[4]在二维空间提出了一种基于复数运算的SME方法,将原始测量值的横纵坐标值分别表示为复数的实部和虚部,通过复数运算建立同一目标在不同坐标系中状态之间的联系,并且构造出了基于复数运算的乘积和形式SME。Leven和Lanterman[7]在Lee研究的基础上建立了基于复数运算的幂次和形式SME,并将扩展卡尔曼滤波(extended kalman filter,EKF)与无迹卡尔曼滤波(unscented kalman filter, UKF)对比,仿真发现UKF滤波可能会产生奇异矩阵,而选用EKF滤波效果更好。虽然基于复数运算的SME有效抑制了伪观测量的产生,跟踪效果与Kamen经典的SME相比有了很大改善,但在航迹交叉点附近的跟踪效果还有提升空间。近几年,Baum等[8]针对SME误差期望值和协方差难以有效计算和非线性滤波问题,提出了最优高斯滤波器,由于考虑了新量测方程的高阶项,因而能给出更优估计效果,但该方法在目标数目增多时也存在计算复杂度较高的缺点。

本文利用多项式因式分解的思想构造了一种改进SME,在观测误差服从独立同分布、零均值高斯白噪声前提下,推导出相应的观测误差协方差阵。与现有几种典型SME和JPDA算法仿真对比,验证新算法不仅延续了SME时效性优势,而且跟踪精度基本达到与JPDA相近的水平,有效抑制了航迹交叉时跟踪误差较大现象。

1对称量测方程

1.1基本概念

(1)

式中,T为采样周期。

(2)

式中,IN为N×N的单位阵;0N为N×N的零矩阵;w(k)=[w1(k)w2(k)…wN(k)]T。

(3)

式中,xj(k)表示第j个目标在x轴的坐标值;uj(k)是第j个目标的观测误差,为零均值高斯白噪声;j=1,2,…,N。

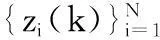
(4)

式中,hi表示第i个对称变换函数;vi(k)为第i个新量测的观测误差。

以一维空间N=2乘积和形式的SME为例,介绍具体构造原理。假设获得量测集为{z1(k),z2(k)},定义新量测

(5)

由式(4)可以得到

(6)

定义新量测矩阵Z(k)=[Z1(k),Z2(k)]T和观测误差矩阵V(k)=[v1(k),v2(k)]T,则观测误差协方差阵R(k)=E[V(k)V(k)T]。

1.2基于多项式思想的SME

以Kamen乘积和形式SME为例[3],在一维空间新量测可以表示为

(7)

式中,xi表示第i个目标的在x轴上的坐标值,i=1,…,N。

这种构造新量测的方法有以下特点:

(1) 新量测通常具有对称性,其对称性表现为新量测与原始测量数据的输入顺序无关,不会随着原始测量数据顺序的变化而发生改变。

(2) 从原始量测变换到新量测过程中信息应当是完整而没有丢失,即新量测集与原始量测集应当具有一一对应关系。具体表现为:当原始量测集已知时,可以确定与其对应的新量测集;而当新量测集作为已知条件时,原始量测集也应当可以求解得到。

由式(7)可以看出,一维空间Kamen乘积和SME显然具有对称性,为验证其原始量测集与新量测集具有一一对应关系,构造关于s的因式:pi=s+xi,则有一元多项式

(8)

Kamen乘积和SME即为多项式系数ai所组成的集合,由于一元多项式与其分解因式之间具有一一对应关系[6],因此从原始测量集变换到新量测集的信息是完整而没有丢失的。

将SME方法推广到二维空间时,较为简单的处理思路是各维独立作SME变换,与之对应的Kamen乘积和SME可表示为

(9)

式中,xi、yi分别是第i个目标的在x轴、y轴上的坐标值,i=1,…,N。

(10)

当新量测集已知时,可以得到x轴和y轴的观测集分别为{x1,x2}和{y1,y2},但无法确定同一目标不同坐标之间的关系,即两个目标的组合形式不仅有{(x1,y1), (x2,y2)},而且还有可能存在{(x1,y2), (x2,y1)}的形式。在跟踪过程中显然不希望后一种组合方式出现,而这种被称之为“鬼点”的坐标会对结果产生不良影响,尤其是在航迹交叉时表现更为明显。因此,需要改进SME方法,使这种“鬼点”坐标越少越好。

2改进SME跟踪算法

2.1改进SME

在二维空间提出一种基于分解因式的改进思路,以提高新量测集的信息完整性。构造因式:qi=s+txi+yi,其中,xi、yi分别表示第i个目标的在x轴、y轴上的坐标值;i=1,…,N。于是有多项式

(11)

新量测集即为多项式系数bij所组成的集合,当N=2时,新量测可以表示为

(12)

由于观测量中包含Kamen乘积和SME,因此,当新量测集已知时,容易得到x轴和y轴的观测集分别为{x1,x2}和{y1,y2},并且新量测通过最后一项加强了不同坐标之间的关系。假设不同坐标之间的关系并不明确,{(x1,y2), (x2,y1)}的组合的形式仍然不能被消除,则有

(x1y1+x2y2)-(x1y2+x2y1)=0

(13)

式(13)表明,当x1=x2或y1=y2时,这种坐标间关系不明确的情况才会发生。然而,一旦x1=x2或y1=y2,集合{(x1,y1), (x2,y2)}与{(x1,y2), (x2,y1)}并没有区别。因此,改进算法能够有效抑制“鬼点”现象,提高新量测集的信息完整性。

2.2观测误差协方差阵

由于观测方程发生改变,与之相应的观测误差协方差阵也要做出调整。但是经过对称变换的观测方程其观测误差往往不再服从高斯分布,在计算时却通常视作高斯分布近似处理[9],难点是新量测误差协方差阵的求解十分困难。

假设在一维空间含误差的原始量测值zi=xi+ui,其中,i=1,…,N;xi为真实值,ui为观测误差。则经过hi对称变换后的新量测误差vi由文献[3]式(28)泰勒公式展开

vi=

(14)

设新量测的观测误差向量V=[v1,…,vn]T,其中,n为新量测方程个数,通过R=E[VVT]可求得新观测误差协方差阵。根据式(14)可知,V为多项式向量,则VVT为多项式矩阵,文献[10]定理1给出了当变量服从高斯分布时,求解多项式期望的方法。

定理 1假设u=[u1,…,um]T~N(μ,Σ),Σ为m×m的半正定矩阵,对于非负整数s1,…,sm,有

(15)

对于如式(12)所示的新观测方程,设初始观测误差向量u=[ux1, ux2, uy1, uy2]T为零均值高斯白噪声,且满足独立同分布,即

(16)

式中,σ为初始观测噪声标准差。

则新的观测误差协方差阵有

R=E[VVT]=

(17)

式中,H(x1,x2,y1,y2)是h(x1,x2,y1,y2)的Jacobian阵。

3仿真分析

考虑二维空间上两个匀速直线运动的目标,设定初始位置和速度以保证两目标能够发生航迹交叉。另外,在真实位置的基础上附加独立同分布、零均值高斯白噪声作为原始测量数据。目标1初始状态为:X1=[500,20,0,30]T,目标2初始状态为:X2=[0,40,500,10]T,当采样周期T=1s,观测噪声标准差σ分别为50m、100m时,原始观测值和真实值如图1所示。

图1　目标观测值与真实值

假设跟踪时无差别地获取两个目标的量测值,且量测与目标的对应关系未知,不考虑虚警和漏警的情况。经过改进SME算法滤波后的效果图如图2所示。

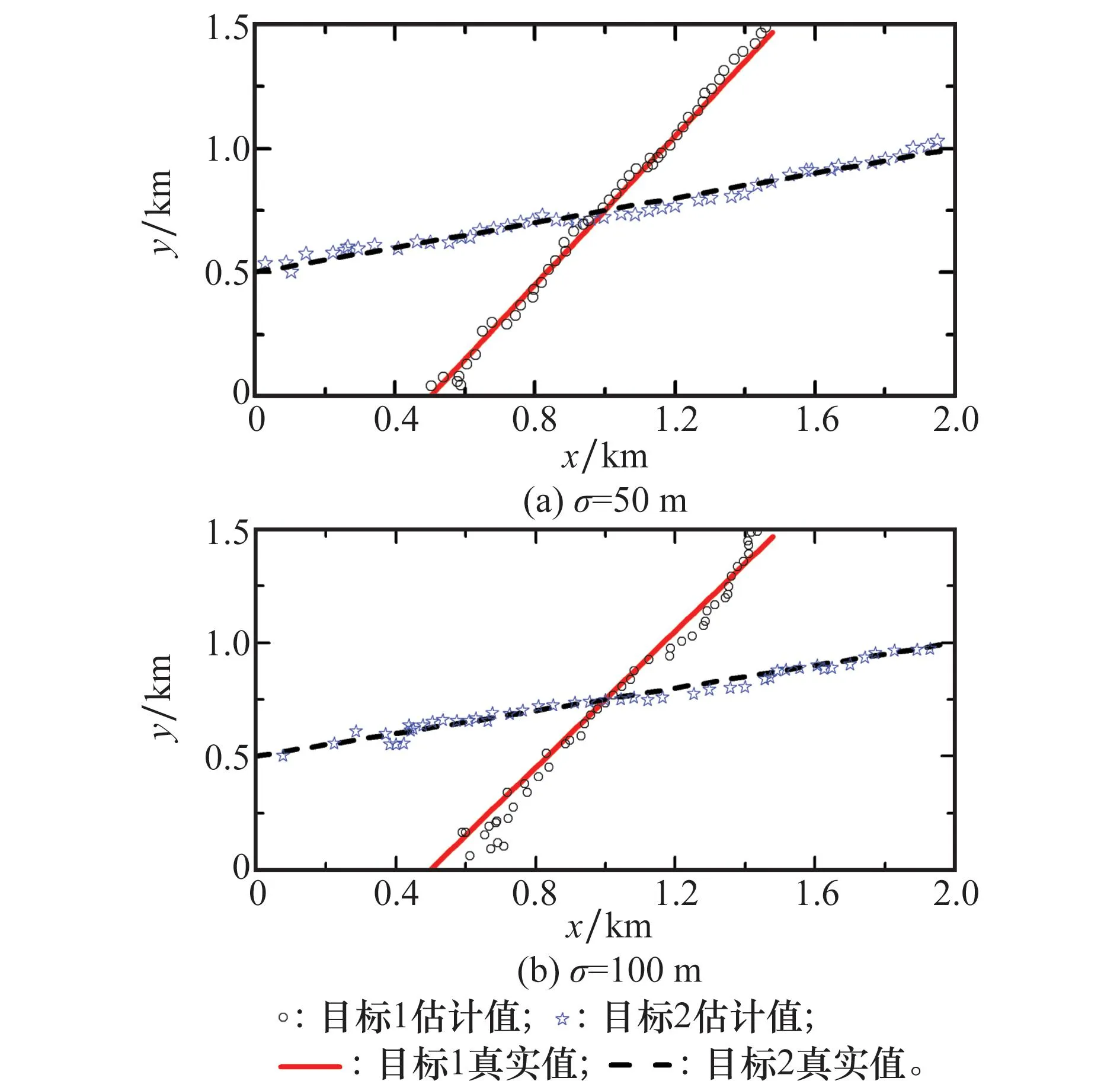
图2　跟踪效果图

由图2中可看出:改进算法在不同观测噪声下都能基本实现对两个目标的跟踪,当观测噪声比较小时,跟踪的比较稳定,但随着噪声的增大,跟踪的精度也逐渐降低。

为了评估改进算法的跟踪效果,将改进SME算法与Kamen乘积和SME[3]、复数乘积和SME[4]以及JPDA算法进行比较。分别在观测噪声标准差σ=50m和σ=100m条件下,进行100次蒙特卡罗仿真,以目标1为例,各算法的位置均方根误差如图3所示。

图3　各算法对目标1跟踪误差图

由图3中可看出:当观测误差较小时,几种算法的跟踪效果相差不大,仅在航迹交叉点附近有不同程度的差别;当观测误差较大时,改进SME算法跟踪精度明显比Kamen乘积和SME、复数乘积和SME算法的跟踪精度要高,基本达到与JPDA相近的水平。当然,评判一个算法的优劣不能仅仅考虑跟踪精度,其时效性也是极为重要的指标。分别取不同次数的蒙特卡罗仿真,统计各复数运算SME和JPDA算法的总运行时间如表1所示。

表1　各算法总运行时间比较　s

由表1可以看出:随着仿真次数的增加,各算法的运行时间逐渐增大,同一仿真次数下SME算法运行时间相差不多,改进SME算法比基于复数运算SME算法的时间性能还要好一点,而JPDA算法的运行时间要比其他3种算法的运行时间大很多,这是由于JPDA涉及数据关联,而其他3种算法不需要数据关联运算,因此基于SME算法在时效性方面比JPDA算法更有优势。

4结论

本文介绍了一种基于SME的多目标跟踪算法,该算法不需要复杂的数据关联运算就能同时对多个目标进行跟踪。针对现有SME的不足之处,构造了一种基于多项式因式分解思想的改进SME,在观测误差服从独立同分布、零均值高斯白噪声前提下,推导出相应的观测误差协方差阵。

在不同观测噪声下对存在航迹交叉的两个目标进行跟踪,取得了较好的跟踪效果,验证了新算法的有效性;与现有SME算法和JPDA算法对比,新算法不仅延续了SME时效性优势,而且跟踪精度基本达到与JPDA相近的水平,有效抑制了航迹交叉时跟踪误差较大现象。然而新算法也存在一些不足,比如:构造的新观测量数目比现有SME要多一些,而且利用改进算法进行多目标跟踪时,目标数目必须已知。

目前SME算法发展并不成熟,许多问题还没有很好的解决,比如:存在虚警漏警时计算较为复杂、目标数目未知情况下应用受限等。因此,需要投入更多的精力去了解、研究SME算法,使之成为一种成熟的理论,以便更好地解决多目标跟踪问题。

参考文献：

[1] Shalom Y B, Daum F, Huang J. The probabilistic data association filter[J].IEEETrans.onControlSystemsMagazine, 2009，29(6): 82-100.

[2] Kamen E W. Multiple target tracking based on symmetric mea-surement equations[J].IEEETrans.onAutomaticControl, 1992, 37(3): 371-374.

[3] Kamen E W, Sastry C R. Multiple target tracking using pro-ducts of position measurements[J].IEEETrans.onAerospaceandElectronicSystems, 1993, 29(2):476-493.

[4] Lee Y. The SME filter approach to multiple target tracking with false and missing measurements[D]. Georgia: School of Electrical and Computer Engineering, 1994.

[5] Kamen E W, Su J K.Introductiontooptimalestimation[M]. London: Springer-Verlag, 1999.

[6] Muder D J, O’Neil S D. The multi-dimensional SME filter for multi-target tracking[C]∥Proc.oftheSPIESignalandDataProcessingofSmallTargets, 1993: 587-599.

[7] Leven W F, Lanterman A D. Multiple target tracking with symmetric measurement equations using unscented Kalman and particle filters[C]∥Proc.ofthe36thSoutheasternSymposiumonSystemTheory, 2004:195-199.

[8] Baum M, Noack B, Beutler F, et al. Optimal Gaussian filtering for polynomial systems applied to association-free multi-target tracking[C]∥Proc.ofthe14thInternationalConferenceonInformationFusion, 2011:1-8.

[9] Leven W F. Approximate Cramer-Rao bounds for multiple target tracking[D]. Georgia: School of Electrical and Computer Engineering, 2006.

[10] Raymond K. From moments of sum to moments of product[J].JournalofMultivariateAnalysis, 2008, 99(3): 542-554.

吴潇(1991-),男,硕士研究生,主要研究方向为多目标跟踪。

E-mail:february27th@163.com

黄树彩(1967-),男,教授,博士,主要研究方向为系统辨识与模式识别、目标检测与跟踪。

E-mail:hsc67118@126.com

凌强(1990-),男,硕士研究生,主要研究方向为红外弱小目标检测与跟踪。

E-mail:lq910131@gmail.com

钟宇(1987-),男,博士研究生,主要研究方向为系统建模与仿真、天基红外预警探测与跟踪。

E-mail:zhongyu257678@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150818.1519.012.html

Multiple targets tracking using modified symmetric measurement equations

WU Xiao, HUANG Shu-cai, LING Qiang, ZHONG Yu

(AirandMissileDefenseCollege,AirForceEngineeringUniversity,Xi’an710051,China)

Abstract:The classical symmetric measurement equation (SME) approach will produce pseudo-measurements while tracking multiple targets in multi-dimensions, which induces large tracking errors around the coordinate switching areas. To solve this problem, a modified SME is proposed by polynomial factoring to connect states of one target with different coordinates. As a result, the mapping relationships of original observations to new mesurements are described more precisely. The new measurement noise covariance matrix is deduced corresponding to the new SME measure noises which are derived by Taylor series expansions. Finally, simulations are constructed to validate the new SME’s characteristics by comparing with the existing SME approaches and joint probability data association algorithm respectively. Results show that the modified SME approach not only maintains the advantage of real-time performances, but also does well in improving tracking accuracy during the coordinate switching areas.

Keywords:symmetric measurement equation (SME); multiple targets tracking; polynomial factoring

作者简介：

中图分类号：V 249

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.04

基金项目：航空科学基金(20130196004)资助课题

收稿日期：2015-01-13；修回日期：2015-06-29；网络优先出版日期：2015-08-18。