基于四元数MUSIC的锥面共形阵列极化-DOA联合估计

刘　帅, 闫锋刚, 金　铭, 乔晓林

(哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209)



基于四元数MUSIC的锥面共形阵列极化-DOA联合估计

刘帅, 闫锋刚, 金铭, 乔晓林

(哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209)

摘要：基于交叉偶极子构成的锥面共形阵列,建立了四元数表示的锥面共形阵列模型并提出了四元数多重信号分类 (multiple signal classification,MUSIC)算法。算法通过同极化子阵的构造以及秩损原理实现了导向矢量中极化信息和波达方向(direction of arrival,DOA)信息的剥离,进而得到入射信号的二维DOA估计和极化参数估计,有效降低了极化-DOA联合估计的计算量。仿真结果验证了算法的有效性。

关键词：锥面共形阵列; 四元数; 极化-DOA联合估计

0引言

由于具有满足空气动力学要求、节省空间、减轻重量、极化敏感、充分利用孔径改善波达方向(direction of arrival,DOA)估计精度等优点,共形阵列[1]在军事、航空、航天、通信等领域具有广阔的应用前景。电磁波极化信息包括极化角和极化相位,其在军事上的应用可以提高地基雷达的抗干扰能力,提高机载雷达抑制地杂波和区分目标的能力,提高侦测系统信号分选与识别能力等;在移动通信中的应用,可以克服共信道干扰和多径衰落干扰,提高信道利用率,提高通信质量。锥面共形阵列作为共形阵列的典型代表,在机载、弹载等平台上有广泛的应用前景。因此，开展基于锥面共形阵列的多参量估计算法研究具有十分重要的意义。

目前在共形阵列的研究方面,已取得较多的研究成果[2-12]。其中文献[2]采用流形分离技术(manifold separation technique, MST)实现了共形阵列下全极化和差波束形成;文献[3]利用线性约束最小方差(linearly constrained minimum variance, LSMV)准则实现了共形阵列条件下的宽带自适应波束形成;文献[4]采用基于遗传算法的投影方法,实现了共形阵列条件下的低旁瓣波束形成。在锥面共形阵列参数估计方面,文献[5]利用锥面共形阵列的多极化特性,结合多重信号分类 (multiple signal classification,MUSIC)算法实现了对入射信号的极化-DOA联合估计;文献[6]针对电磁偶极子构成的锥面共形阵列,先由坡印廷矢量得到信号到达角的粗略估计,再对下圆环子阵解相位模糊,最终得到DOA的精确估计值;文献[7]通过阵元结构设计,给出了基于旋转不变子空间算法(estimation of signal parameters via rotational invariant techniques, ESPRIT)的锥面共形阵列解相干空间平滑算法,实现了相干信源的高分辨DOA估计;文献[8]通过空间平滑实现了信源的解相干,由ESPRIT算法完成了多个相干信源DOA和极化参数的联合估计。此外,文献[9]实现了共形阵列条件下宽带信号的波束扫描,其1 dB增益带宽达到20%;文献[10]通过MST技术实现了球面共形阵列条件下的稳健的波束形成算法;文献[11]利用四阶累积量和旋转不变子空间算法实现了共形阵列(锥面、柱面、球面)条件下的盲极化DOA估计;文献[12]首先对柱面共形阵列进行建模,然后通过旋转不变子空间算法实现了对入射信号DOA和极化参数的估计。

综上,基于锥面共形阵列的多参量联合估计算法大多通过ESPRIT算法实现,在多参量估计过程中需要参数配对;而基于MUSIC的多参量估计算法需要在二维极化域和二维DOA域构成的四维空间内寻优,计算量巨大。

四元数是一种长复数的表示形式,将其应用于极化敏感阵列可以实现对色噪声的有效抑制以及降维参数估计等。在极化敏感阵列多参量估计方面,文献[13]提出了四元数模型下的矢量传感器信号建模和处理的新方法。此后文献[14]通过定义四元数的相关函数,利用四元数MUSIC算法在高斯背景下有效地估计出了信号参数。国内方面,文献[15]针对极化敏感阵列,通过八元数的定义以及相应矩阵的特征值分解实现了八元数MUSIC算法,该方法相对于经典长矢量算法有效地提高了参数估计性能。文献[16]在建立电磁矢量传感器阵列四元数模型的基础上,利用四元数-MUSIC方法实现了参数估计的降维处理,降低了极化-DOA联合估计算法的计算量。综上,基于四元数的多参量估计算法主要通过对导向矢量的四元数表示,将极化参数与DOA参数的“去耦合”,进而得到多参量估计结果。由于锥面共形阵列的特点导致其全局坐标系下阵元的极化形式不完全一致,因此已有的四元数MUSIC算法无法应用于锥面共形阵列。

本文首先建立了由四元数表示的锥面共形阵列信号模型,然后通过构造若干同极化子阵并结合秩损理论给出了基于锥面共形阵列的四元数MUSIC算法,实现了极化和DOA参数联合估计的降维处理。算法先估计入射信号的DOA参数,再由文献[5]中给出的长矢量MUSIC算法估计信号的极化参数,有效地降低了计算量,且自动完成参数配对。最后通过仿真实验比较了四元数MUSIC算法和长矢量MUSIC算法的估计精度。

1四元数定义及性质

(1) 四元数定义

设q=a+bi+cj+dk,a,b,c,d∈R,若i,j,k满足:i2=j2=k2=-1,其中ij=-ji=k,jk=-kj=i,ki=-ik=j则称数q为四元数,称a为四元数q的实部,称bi+cj+dk为q的虚部。

(2) 四元数矩阵的特征值分解

(1)

(2)

2基于四元数的锥面共形阵列模型

2.1双极化锥面共形阵列

双极化锥面共形阵列由交叉偶极子在锥面载体共形形成,其具体形式如图1所示[2,5],圆锥顶点处存在一个阵元,其下排列了若干圆环阵,n为由上至下的圆环阵序号,d为圆环阵间距离,每个圆环阵包含8个阵元,每个圆环阵中阵元序号m按逆时针方向排序,起始阵元位于X正半轴上,β为圆锥顶角的1/2。阵元坐标可表示为

(3)

(4)

(5)

图1　双极化锥面共形阵列示意图

2.2双极化锥面共形阵列信号模型

假设有M个信号入射到由N个双极化阵元构成的锥面共形阵列,其信号模型[5]可表示为

(6)

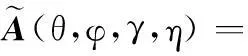
(7)

(8)

式中,“⊙”为矩阵的Hadamard乘积;a(θi,φi)为导向矢量中与入射信号DOA相关的空域信息(具体形式见文献[5]);p(θi,φi,γi,ηi)为导向矢量中的极化信息,可表示为

(9)

(10)

由以上讨论可知,式(8)所示的双极化锥面共形阵列导向矢量中的每个元素代表双极化阵元的一个极化单元对入射信号的响应,因此对N个双极化阵元构成的共形阵列而言,其导向矢量的维数为2N。

2.3双极化锥面共形阵列四元数模型

对于锥面共形阵列中的第k个双极化阵元,其两个极化单元对第i个信号源的响应可以用一个二维列向量表示为

(11)

将pki用四元数表示为

(12)

此时,阵列的导向矢量用四元数表示为

(13)

(14)

(15)

式中，k和l分别为入射信号方向矢量和阵元的位置矢量,具体定义见文献[5]。

观察式(13)可以发现,由于锥面共形阵列中每个双极化阵元受载体曲率的影响,使阵元在全局坐标下具有不同的极化状态。对同一个入射信号而言,共形阵列中阵元的极化响应不同,所有阵元的极化响应不能用一个四元数表示,而应为式(15)所示的四元数向量。此时四元数定义下的锥面共形阵列信号模型可以表示为

(16)

式中

(17)

(18)

式(18)为噪声向量在四元数模型下的表示,其中元素可以表示为

(19)

式中,nih(t)和niv(t)表示叠加在第i个阵元两个极化单元上的复噪声。

与共形阵列不同,文献[16]给出的由偶极子构成的传统极化敏感阵列,其四元数定义下的导向矢量表示为

(20)

综上,完成了双极化锥面共形阵列在四元数定义下的信号建模。对比式(13)和式(20)可知,共形阵列四元数模型与一般极化敏感阵列的四元数模型差别在于:由于共形载体曲率的影响,阵元的方向图发生旋转,使得共形阵列中不同阵元感受到入射信号的极化信息不同,不能使用一个四元数表示所有阵元的极化输出;而对一般极化敏感阵列来说,由于每个阵元的摆放形式一致,阵列中所有阵元感受到的入射信号极化信息相同,可以使用一个四元数表示所有阵元的四元数输出。因此传统的降维四元数MUSIC算法无法直接应用于共形阵列,需要研究一种适用于双极化锥面共形阵列的降维四元数MUSIC算法。

3基于锥面共形阵列的四元数MUSIC算法

3.1传统极化敏感阵列的四元数MUSIC算法

文献[16]给出了基于传统极化敏感阵列的四元数算法,其主要处理过程为:计算阵列的四元数自相关函数

(21)

(22)

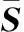
(23)

将式(20)代入式(23),并整理可得

(24)

其中

(25)

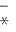
(26)

由式(26)构造的空间谱函数在(θ,φ)二维搜索得到M个极大值即对应信号的入射方向。在得到二维DOA估计值后,将其代入联合谱中做(γ,η)两维的逐个搜索即可估计得到信号的极化参数。

3.2锥面共形阵列的四元数MUSIC算法

由第2节讨论可知,锥面共形阵列四元数模型与一般极化敏感阵列四元数模型相比,差别主要在于共形载体曲率导致的阵元方向图的旋转,使共形阵列导向矢量的表达形式不同于一般极化敏感阵列,传统四元数MUSIC算法无法直接应用。本文根据锥面共形阵列特点,从布阵形式入手,结合秩损原理[17],实现了锥面共形阵列下的四元数MUSIC算法。

考虑对锥面共形阵列构造极化形式相同的子阵,构造方法如图1所示。由共形阵列的建模过程可知[2,5],图1中的锥面共形阵列,除去原点处阵元,S1、S2、S3 3条母线上各自的阵元具有相同的极化形式。

假设锥面共形阵列共有L条母线,每条母线上的阵元个数为K,则锥面共形阵列的阵元数N=L×K+1。由式(13)~式(15)可知,此时锥面共形阵列的导向矢量可以表示为

(27)

式(27)可重写为

(28)

式中

(29)

其中

(30)

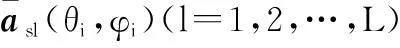
(31)

将式(28)代入到式(23)中,整理可得

(32)

式中

(33)

(34)

式中,det[·]表示求行列式值。

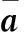
(35)

根据四元数矩阵行列式与矩阵特征值关系,可得对入射信源的二维DOA估计为

(36)

式中,λmin{·}为求矩阵的最小特征值。

在得到入射信号源的DOA估计结果后,即可使用MUSIC算法[5]实现对极化参数的估计

(37)

综上,可得四元数MUSIC算法的具体步骤为:

步骤 5将得到的入射方向估计值分别代入式(37),做极化参数的二维搜索得到与入射信号对应的极化参数估计值。

4仿真实验

(1) 验证四元数MUSIC算法的有效性。仿真中取双极化锥面共形阵列，形式如图1所示,具体参数为:β=20°,圆环阵个数3,由上至下每个圆环均匀分布8个阵元。圆环阵之间的高度为2.75λ,最底层圆环阵的半径为3λ,λ为入射信号波长。

假设有两个独立信号源入射到阵列,入射参数分别为(θ1,φ1,γ1,η1)=(15°,50°,45°,90°),(θ2,φ2,γ2,η2)=(35°,150°,70°,0°),信噪比均为10 dB,快拍数为500。可由四元数MUSIC算法得到阵列的估计结果如图2所示。

图2　双极化锥面共形阵列四元数算法结果图

由图2(a)的仿真结果可以看出,对于两个不同极化的入射信号,通过四元数降维算法在角度域形成了二维谱峰,谱峰位置分别为(15°,50°)和(35°,150°)与仿真中设置的信号入射方向相同。

四元数MUSIC算法在得到入射信号的两个DOA估计值后,将其分别代入式(37)描述的联合谱中,做极化域的二维搜索可得对入射信号极化参数的估计结果如图2 (b)和图2(c)所示,可分别得到两个信号的极化参数估计结果为 (45°,90°)和(70°,0°)。由于在极化域搜索时,已知信号的DOA信息,因此四元数MUSIC算法自动实现了极化-DOA参数的配对。

对共形阵列而言,在采用文献[5]中的MUSIC算法估计信号极化和DOA参数时,需要做极化和DOA参数的四维搜索。以两个入射信号,1°搜索步长为例,极化-DOA联合谱估计算法[5]需要计算的谱值点数为90×360×91×360=1 061 424 000。在采用四元数算法时做二维DOA搜索时,所需计算的谱值点数为97 920点(二维DOA搜索需90×360=32 400,两次二维极化搜索需2×91×360=65 520),可以看出,四元数降维算法大大降低了参数估计所需的计算量。

综上分析可知,四元数算法可以将极化信息剥离,先估计入射信号的二维DOA参数,在此基础上,可以由联合谱算法分别得到入射信号的极化参数估计结果,与联合谱算法所需的四维搜索不同,四元数算法大大降低了锥面共形阵列条件下参数估计的计算量。仿真结果证明了算法的有效性。

(2)考察算法参数估计精度与SNR关系。假设有一个信号源入射到阵列上,参数为(θ1,φ1,γ1,η1)=(30°,85°,65°,120°),阵列接收的快拍数为200,信噪比从0 dB开始以2 dB为间隔增加到20 dB,在每个信噪比上独立实验200次,统计参数估计的均方根误差,仿真结果如图3所示。

图3　参数估计精度随信噪比变化关系

由图3的仿真结果可以看出,信噪比较低时,四元数MUSIC算法的DOA和极化参数估计精度略逊于MUSIC[5];在信噪比大于15dB时,四元数MUSIC算法的估计精度接近MUSIC算法[5]。综上,总体上看四元数MUSIC算法的估计精度低于MUSIC,但考虑到四元数算法的降维过程大大降低了参数估计的计算复杂度,在实际应用中仍不失为一种较好的选择。

5结束语

本文针对的双极化锥面共形阵列的特点,建立了阵列的四元数信号模型,提出了适用于锥面共形阵列的四元数MUSIC算法。算法通过同极化接收子阵的设置及秩损原理完成了导向矢量中极化信息和DOA信息的去耦合,先由四元数MUSIC算法对入射信号的DOA进行估计,再由DOA估计结果及MUSIC算法得到极化参数的估计,实现了DOA参数和极化参数的自动配对;同时方法将极化和DOA域的四维搜索问题转换为2维DOA搜索和2维极化域搜索,大大减小了极化-DOA联合估计的计算量。最后通过仿真实验验证了本文方法的有效性。

参考文献：

[1] Josefsson L, Persson P.Conformalarrayantennatheoryanddesign[M]. Canada: Wiley-IEEE Press,2006.

[2] Huang Z J, Zhou J, Zhang H P. Full polarimetric sum and difference patterns synthesis for conformal array[J].ElectronicsLetters,2015,51(8):602-604.

[3] Rasekh M, Seydnejad S R. Design of an adaptive wideband beamforming algorithm for conformal arrays [J].IEEECommunicationsLetters, 2014, 18(11):1955-1958.

[4] Zeng G Q, Li S Y, Zhang Y, et al. Low side lobe pattern synthesis using projection method with genetic algorithm for truncated cone conformal phased arrays [J].JournalofSystemsEngineeringandElectronics, 2014,25(4):554-559.

[5] Liu S, Zhou H J, Jin M, et al. Polarization-DOA estimation for conical conformal array antennas[J].SystemsEngineeringandElectronics, 2012,33(2):253-257. (刘帅,周洪娟,金铭,等. 锥面共形阵列天线的极化-DOA估计[J].系统工程与电子技术,2012,33(2):253-257.)

[6] Wang L M, Guo L X, Wang G B, et al. Joint multi-parameters estimation method of conical conformal array [P]. China: CN 103278796A,20130904.(王兰美,郭立新,王桂宝,等.锥面共形阵列多参量联合估计方法[P].中国:CN 103278796A,20130904.)

[7] Qi Z S, Guo Y, Wang B H, et al. Blind DOA estimation algorithm of coherent sources for conical conformal array antenna with respect to polarization diversity[J].SystemsEngineeringandElectronics,2011,33(6):1226-1230.(齐子森,郭英,王布宏,等.锥面共形阵列天线相干信源盲极化DOA估计算法[J].系统工程与电子技术,2011,33(6):1226-1230.)

[8] Zhang S Y, Guo Y, Qi Z S, et al. DOA and polarization estimation algorithm for coherent signals with conical conformal array [J].JournalofAstronautics,2012,33(7):956-963.(张树银,郭英,齐子森,等.锥面共形阵列相关源DOA和极化参数的联合估计算法[J].宇航学报,2012,33(7):956-963.)

[9] Li Y J, Li L. Broadband microstrip beam deflector based on dual-resonance conformal loops array [J].IEEETrans.onAntennasandPropagation, 2014, 62(6):3028-3034.

[10] Yang P,Yang F, Nie Z P, et al. Robust beamformer using manifold separation technique for semispherical conformal array [J].IEEEAntennasandWirelessPropagationLetters,2011,10(3):1035-1038.

[11] Qi Z S, Guo Y, Wang B H. Blind direction-of-arrival estimation algorithm for conformal array antenna with respect to polarisation diversity [J].IETMicrowaves,Antennas&Propagation, 2011,5(4):433-442.

[12] Zou L, Lasenby J, He Z. Direction and polarisation estimation using polarised cylindrical conformal arrays [J].IETSignalProcessing, 2012, 6(5):395-403.

[13] Nicolas L B, Jerome M. Signal value decomposition of quaternion matrices: a new tool for vector-sensor signal processing[J].SignalProcessing, 2004, 84(7): 1177-1199.

[14] Sebastian M, Nicolas L B, Jerome I M. Quaternion-MUSIC for vector sensor array processing[J].IEEETrans.onSignalProcessing,2006,54(4):1218-1229.

[15] Le B N, Miron S, Mars J I. MUSIC algorithm for vector-sensors array using biquaternions [J].IEEETrans.onSignalProcessing, 2007,55(9):4523-4533.

[16] Li J S, Tao J W. The dimension reduction quaternion MUSIC algorithm for jointly estimating DOA and polarization [J].JournalofElectronics&InformationTechnology,2011,33(1):106-111.(李京书,陶建武.信号DOA和极化信息联合估计的降维四元数MUSIC方法[J].电子与信息学报,2011,33(1):106-111.)

[17] Marius P, Alex B G, Wong K M. Direction finding in partly calibrated sensor arrays composed of multiple subarrays[J].IEEETrans.onSignalProcessing, 2002,50(9):2103-2115.

刘帅(1980-),男,副教授,博士,主要研究方向为阵列信号处理及自适应波束形成。

E-mail:liu_shuai_boy@163.com

闫锋刚(1982-),男,副教授,博士,主要研究方向为阵列信号处理、遥感图像处理、统计性能及时频域分析。

E-mail:yfglion@163.com

金铭(1968-),男,教授,博士,主要研究方向为雷达信号处理。

E-mail:jinming0987@163.com

乔晓林(1948-),男,教授,博士,主要研究方向为雷达信号处理。

E-mail:paulqiao@sohu.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150818.1519.018.html

Joint polarization-DOA estimation for conical conformal

array based on quaternion MUSIC

LIU Shuai, YAN Feng-gang, JIN Ming, QIAO Xiao-lin

(SchoolofInformationandElectricalEngineering,HarbinInstituteofTechnology(Weihai),Weihai264209,China)

Abstract:Based on conical conformal array with crossed dipole elements, the quaternion array signal model is built, and the quaternion multiple signal classification (MUSIC) algorithm is proposed. This algorithm realizes de-coupling polarization and direction of arrival (DOA) information through resetting the elements with the same polarizations of sub-arrays and the principle of rank-loss, then it obtains the estimations of 2D DOA and the polarization parameter of incident signals. The computational complexity of joint polarization-DOA estimation is reduced significantly. Finally, the simulation result verifies the effectiveness of the method.

Keywords:conical conformal array; quaternion; joint polarization-DOA estimation

作者简介：

中图分类号：TN 911.7

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.01

基金项目：中央高校基本科研业务费专项资金(HIT.NSRIF.2016102)；中国博士后科学基金(2015M571414)；山东省自然科学基金(ZR2014FQ003)；哈尔滨工业大学校科研启动经费(HIT(WH)201411)资助课题

收稿日期：2015-03-12；修回日期：2015-07-15；网络优先出版日期：2015-08-18。