平齐端板连接钢框架梁柱子结构的抗倒塌性能分析
2016-01-21钟炜辉郝际平李超范
孟 宝,钟炜辉,郝际平,李超范
(西安建筑科技大学土木工程学院,陕西 西安 710055)
钢框架结构因意外事件(如爆炸、撞击等)使竖向主要构件(柱)失效,其竖向荷载传递路径将发生变化,结构内力发生重分布,甚至会出现所谓的悬链线机制来形成抗力以承担竖向荷载.此时,梁柱节点性能对整体结构的影响变得尤为突出,并因其鲁棒性不同使结构呈现不同的变形形式[1].平齐端板连接是国内外普遍采用的梁柱节点连接形式之一,因其构造简单、施工方便、受力性能好等优点,被广泛应用于低层及多高层钢框架结构.特别构是该连接方式具有良好的变形能力,当竖向件(柱)失效时易使横向构件(梁)形成悬链线效应,有利于增强结构的抗倒塌能力[2].
近年来,对结构抗倒塌机制的研究已经受到各国学者的高度关注,研究日益深入.Yang[2]、谢甫哲[3]、霍静思[4]等通过试验研究认为悬链线效应的大小在很大程度上取决于节点的延性.王开强[5]、郑阳[6]、何政[7]等通过理论模型分析了钢梁的悬链线效应,指出悬链线效应是结构抵抗倒塌的关键环节.Guo[8]、Kandil[9]、杨卫忠[10]等针对平齐端板连接节点的研究表明,梁跨高比和端板厚度等是影响该节点连接性能以及悬链线效应的主要因素.
目前,针对平齐端板连接节点,国内外研究主要集中在其弯矩-转角性能上,而并未过多地涉及其对结构抗倒塌性能的影响.美国抗倒塌专业规范GSA2003[11]对于钢框架结构仅考虑了梁的受弯性能而忽略了悬链线效应的有利作用,设计结果会偏于保守.为进一步深入研究该连接形式对钢框架结构抗倒塌性能的影响,本文采用备用荷载路径法,通过建立梁柱子结构模型,基于连接节点的破坏模式分析了梁机制与悬链线机制的转换机理.同时,在考虑材料非线性、几何非线性及接触非线性下,建立了数值分析模型,并与文献[2]的试验结果进行了对比验证.在此基础上,分析了梁跨高比和端板厚度等关键参数对梁柱子结构抗倒塌性能的影响,获得了一些有价值的结论,为同类连接形式的钢框架结构抗倒塌分析和设计提供参考.
1 梁柱子结构抗倒塌机制分析
1.1 梁柱子结构模型
当前,对钢框架进行抗倒塌分析和设计通常采用备用荷载路径法(AP法),不考虑柱的失效过程和原因,只考虑与失效柱相连的主要构件在外荷载作用下的性态变化,由此可简单取如图1所示的梁柱子结构进行分析.

图1 梁柱子结构模型Fig.1 Model of beam-column substructure
1.2 基于节点破坏模式的抗倒塌机制分析
梁柱子结构失效时,其节点的破坏方式主要表现为:端板受弯或螺栓受拉失效[2].为研究方便,考虑两边柱的侧向变形,将梁柱子结构进一步简化为两端部带有轴向约束弹簧的计算模型,如图2所示.

图2 梁柱子结构简化计算模型Fig.2 The simplified calculation model of beam-column substructure

图3 梁柱子结构的受力过程Fig.3 The loading process of beam-column substructure
(1)阶段①:梁柱子结构处于弹性状态,主要依靠梁机制形成抗力来抵抗外荷载,此时梁中轴拉力很小,可以忽略不计.失效柱处的竖向荷载F与竖向位移v呈线性变化关系,如图3中的0A段,此时有:


由于梁柱节点处弯矩最大,节点屈服时受弯承载力为MPb.此时,若连接节点的中和轴位于梁上翼缘的上端,如图4中的A-A截面,则可采用组件法得出此连接节点的抗弯承载力[12]:

式中:MPb为连接节点屈服时的受弯承载力;m为螺栓群的列数;n为螺栓群的排数;yi为螺栓中心到中和轴的距离;Fbo,i为每个螺栓对应时由端板和螺栓确定抗拉承载力中的最小值[12],式(3)中前两式分别表示外内排螺栓时端板控制;第三式表示螺栓控制.
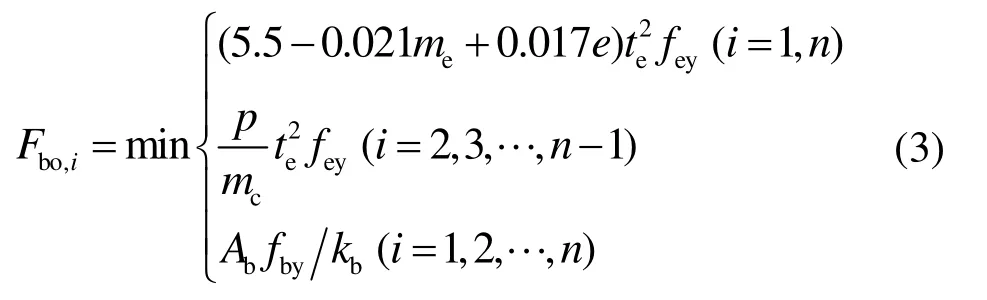
式中:me为螺栓中心至梁腹板边缘的距离;e为螺栓中心至柱翼缘边或端板边距离的较小值;te为端板的厚度,端板厚度过小会使节点局部失效[13],端板过厚会使节点因刚度较大而转动能力减低[14],因而端板厚度应满;d为螺栓的直径;fbu为螺栓的抗拉极限强度;fey为端板材料的屈服强度;p为螺栓间距;mc为螺栓中心至柱腹板边缘的距离;Ab为螺栓横截面面积;kb为考虑螺栓撬力影响的系数,取1.33[12];fby为螺栓屈服强度.

图4 螺栓群中和轴位置Fig.4 Neutral axis position of bolt group
通过简单平衡关系,易知此时(点A)失效柱处的竖向荷载及相应的竖向位移分别为:

(2)阶段②:梁柱节点处出现塑性流动,失效柱处的竖向位移不断增大(如图3中的AB段),此时梁中轴拉力仍较小,悬链线效应尚不显著,结构抗力在此阶段保持不变,则可得该阶段结束时失效柱处相应的竖向位移[15]:

式中:r可近似取为梁高h的一半[15].由此可确定点B.
(3)阶段③:随着竖向变形的继续增大,由梁中轴拉力形成的悬链线效应逐渐显著,即梁机制逐渐向悬链线机制转换,此时由梁柱节点受弯所形成的抗力将逐渐减小[16],梁柱子结构进入图3中的BC段.根据图5所示半结构的简单平衡关系,可得:

式中:M、N分别为梁柱节点处的梁端弯矩和梁中轴力.

图5 阶段③时结构受力图Fig.5 The mechanical equilibrium of the model of stage ③
梁柱节点受弯屈服后在轴拉力作用下,节点处的轴力和弯矩相关关系可表示为[16]:
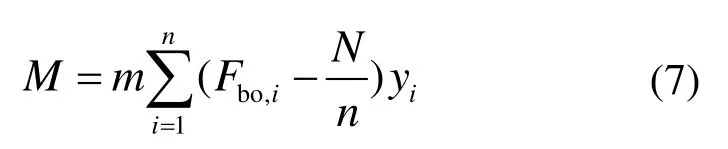
由图6所示的几何关系近似可得半跨梁轴向位移为:


图6 阶段③时梁的变形Fig.6 The deformation diagram of stage ③
梁轴向水平位移主要由梁弹性伸长量de和梁柱节点处的塑性变形dp组成,即:

梁内轴力仅与单元弹性伸长有关,所以

式中:Ka为梁的等效轴向刚度,按下式计算:
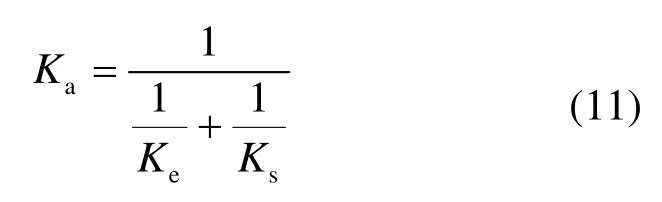
式中:Ke为梁的轴向刚度,;Ks为梁的轴向约束刚度[17].
对式(10)求导可得:
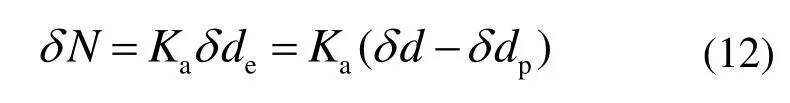
塑性变形主要发生在失效柱两侧,假设梁柱节点处塑性极限弯矩MPb和梁中塑性极限轴力NPb的比值为rp,即.则由内力屈服曲线对应的流动法则可知,梁柱节点处塑性变形为:

对式(12)积分得:

由式(6)、(7)、(14)联立可得:
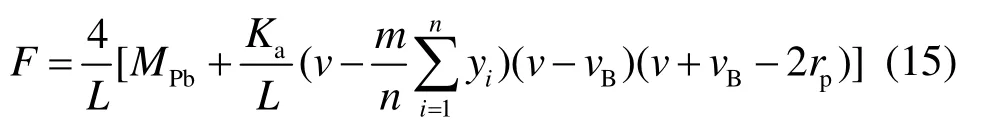
随着梁机制逐步向悬链线机制转换,梁机制逐渐退出工作,悬链线机制愈发显著,表现为梁柱节点处螺栓全部受拉屈服,即梁中轴力(de为螺栓有效直径),弯矩趋近于零,到达C点.将式(7)、(14)代入式(6),并注意此时,即可简单得到FC的计算结果.
(4)阶段④:梁机制已退出工作,悬链线机制继续发挥作用,表现为梁中以轴拉力NPb为主,可忽略弯矩.此时,竖向承载力和竖向位移的关系可表示为:

只要节点有足够的转动能力而不发生破坏,则最终竖向承载力将趋近于2NPb.
2 平齐端板连接梁柱子结构数值模型及验证
钢框架结构抗倒塌设计中需要明确具体的抗力机制,掌握不同抗力机制的转化机理,因此涉及到较强的非线性分析,同时也要充分考虑钢梁线刚度、节点性能和结构破坏模式等因素的影响,很难给出内力和变形的准确解析解.本节利用非线性有限元程序ABAQUS对梁柱子结构在竖向荷载作用下的抗力机制进行分析,从而考察悬链线效应对结构抗倒塌性能的影响.
2.1 数值模型的建立
由于结构对称,可取如图1所示梁柱子结构的1/2建立数值模型.为减少节点和单元数,将梁分为两部分,与柱相连的部分采用C3D8R实体单元,另一部分采用B31梁单元,柱、端板及螺栓均采用C3D8R实体单元.各部件的连接面采用面面接触,切线方向为库伦摩擦接触,法线方向设为“硬”接触.数值模型中根据梁柱子结构的实际约束情况将梁端设为铰接,柱对称面设为竖向滑动约束,在柱顶采用位移加载.平齐端板连接数值模型的单元划分及边界条件如图7所示.

图7 平齐端板连接的数值模型Fig.7 Numerical model of flush end plate connection
2.2 数值模型的验证
Yang和Tan曾就平齐端板连接梁柱子结构进行了试验研究[2](简称YT试验),试件及节点几何尺寸如图8所示.试件中,钢梁和钢柱均为S355钢材,其截面尺寸分别UB 254 mm×146 mm×37 mm和UC 203 mm×203 mm×71 mm(梁、柱均截面采用英国标准型H形钢);端板为S275钢材,截面尺寸为306 mm×200 mm×12 mm,弹性模量为200 GPa;螺栓采用8.8级M20,其屈服强度为640 MPa,抗拉极限强度为800 MPa,由于螺栓手动拧紧,因此不考虑螺栓的预拉力[2].采用与YT试验相同的构件尺寸及材料性能来建立数值模型,钢材本构关系采用理想弹塑性模型,不考虑焊接残余应力的影响.

图8 试件尺寸及节点详图Fig.8 Specimen size and detail diagram of joint
YT试验中梁柱子结构因螺栓在拉弯组合内力作用下在第③阶段结束时发生受拉破坏,图9给出了平齐端板连接的破坏模式,可见数值模拟结果与YT试验的破坏现象十分吻合.

图9 数值分析与YT试验关于破坏模式对比Fig.9 Comparison of failure mode between numerical analysis and YT test

图10 理论、数值分析与YT试验关于竖向承载力-位移曲线对比Fig.10 Comparison of the vertical bearing capacity-displacement curve among theory,numerical analysis and YT test
由图10可以看出,数值和理论分析得到的竖向承载力-竖向位移曲线的变化趋势与YT试验结果相吻合.此外,由表1可得螺栓受拉失效时,数值和理论分析所获得的计算结果与YT试验值十分接近.由上述结果可以看出,数值分析模型的正确性,同时可用上述理论计算公式获得结构的抗倒塌性能.相比较而言阶段③时理论计算值和数值分析与YT试验的结果偏差较大,这可能是因为此阶段梁机制与悬链线机制共同作用下,两端水平侧约束刚度对梁柱子结构竖向承载力的影响所造成的.

表1 理论、数值分析计算结果与YT试验值对比Tab.1 Comparison of results among theory,numerical analysis and YT test
3 平齐端板梁柱子结构抗倒塌性能的影响因素分析
Yang[18]对平齐端板连接梁腹板螺栓布置进行了有限元分析,而未考虑梁跨高比和端板厚度对梁柱子结构抗倒塌性能的影响.因此,在YT试验基础上,本节针对梁跨高比和端板厚度对平齐端板连接钢框架抗倒塌性能的影响进行深入分析.
3.1 梁跨高比的影响
梁跨高比是影响梁柱子结构抗倒塌性能的重要因素,基于YT试验,在不改变梁截面高度下设立了5组不同的跨高比情况,其数值分析和理论计算结果如图11和表2所示.
数值分析过程中构件在极限状态下均因螺栓受拉屈服而失效.从图11可以看出,随着梁跨高比的增大,梁柱节点转角减小,梁柱子结构由梁柱节点受弯性能形成抗力的能力逐渐减小,梁呈现二力杆受拉效应显著,主要通过悬链线机构来形成抗力.上述表明了过大的梁跨高比,并不利于悬链线机制发挥作用.

图11 不同梁跨高比下竖向承载力-节点转角曲线Fig.11 The component force –rotation curve under different span-to-depth ratio of beam

表2 不同跨高比下分析结果对比Tab.2 Comparison of the results under different span-to-depth ratio
从表2的计算结果可以看出,当梁跨高比由10到30发生变化时,出现了竖向位移增大而竖向承载力反而减小的现象,这主要是因为用于抵抗失效柱处由竖向荷载引起的梁内拉结力竖向分量,会随着梁跨高比的增大要求有更大的竖向变形.另外,跨高比对梁柱节点转角影响较大,随着跨高比的增加梁柱节点转角逐渐减小.对于平齐端板连接梁柱节点塑性极限转角,GSA2003仅考虑受弯时的塑性转角,没有考虑悬链线阶段节点的转动能力,因而其计算结果过于保守.梁柱子结构的竖向承载力达到峰值时(螺栓失效)相应的竖向位移约为跨长的1/5~1/10,此即为钢框架悬链线机制的极限变形状态.
针对不同的跨高比,表2还列出了梁柱子结构在极限状态下的理论计算的结果,以便与数值模拟结果进行对比,可见理论计算结果与数值分析结果相接近,满足一般梁跨高比的精度要求.可依此按理论计算公式初步估算螺栓受拉破坏模式下的极限变形和抗倒塌承载力.
3.2 端板厚度的影响
为研究端板厚度对平齐端板连接梁柱子结构抗倒塌性能的影响,在YT试验基础上,改变端板的厚度,设立5个不同的对比组(见表3),其数值分析结果见表3和图12.

表3 不同端板厚度的分析结果对比Tab.3 Comparison of the results under different thickness of end plate
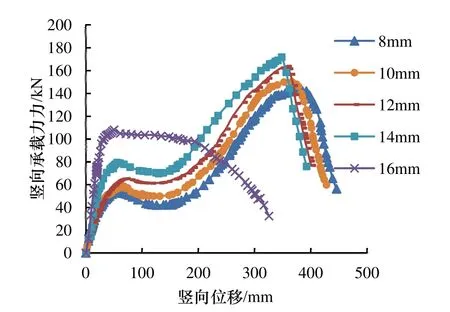
图12 不同端板厚度时竖向承载力-位移曲线Fig.12 The force-displacement curve of different thickness of end plate
端板厚度对平齐端板连接性能的影响较为显著,当端板厚度为8~14 mm时,随着端板厚度的增加,节点的转动刚度增大,使得竖向承载力逐渐增大,竖向位移及节点塑性转角逐渐减小.当端板厚度大于16 mm时,失效柱的最大竖向承载力、竖向位移和节点的转角均大幅下降.这是由于端板厚度的过大,使得端板的抗弯刚度显著增大而变形较小.当螺栓承受的拉力超过承载力值时,悬链线机制未得到发展,停留在阶段②.相反,当端板厚度过小时,梁中轴力的存在,使得端板接触面上下端与柱翼缘板分离,端板将首先达到极限状态从而造成节点的局部破坏,使得平齐端板连接的整体延性减低,同样不利于悬链线机制发挥作用.因此,适宜的端板厚度对平齐端板连接节点的受力性能非常重要,不仅能使螺栓和端板的承载力得到充分利用,而且能够保证结构具有较好的延性,使梁能在大变形状态下通过悬链线机制来抵抗外载.
另外,表3还列出了不同端板厚度时的理论计算结果,以便与数值分析结果进行对比.由于式(3)中te的取值只考虑梁柱节点在受弯状态下的转动变形而未考虑悬链状态下节点的塑性变形,结果偏于保守,因此可适当放宽te的取值.当端板厚度在8~14 mm时,理论计算与数值分析结果相吻合.当端板厚度大于16 mm时,底部螺栓在阶段①因弯矩作用下受拉而发生破坏,未形成显著的悬链线效应.
4 结论
对平齐端板连接梁柱子结构的抗倒塌机理进行了分析,有以下几点结论:
(1)通过对钢框架结构抗倒塌机制的力学机理进行分析,基于平齐端板连接梁柱子结构的破坏模式,给出了四阶段抗倒塌分析的简化模型,分析了梁机制向悬链线机制转换的机理,可以此初步估计钢框架的抗倒塌性能.
(2)通过数值分析得,梁跨高比对平齐端板连接钢框架梁柱子结构抗倒塌性能的影响较大:当梁跨高比由10~30发生变化时,梁柱子结构受弯抵抗外载的能力逐渐减小,主要通过悬链线机制来抵抗外载,而且子结构的竖向承载力达到峰值荷载时,相应的竖向位移约为跨长的1/5~1/10.
(3)端板厚度对平齐端板连接钢框架梁柱子结构的影响较显著,当端板过薄或过厚时,会限制悬链线机制作用的发挥,不利于结构的抗倒塌性能,因此在节点设计时要选择合适的端板厚度.
References
[1]李玲,王伟,陈以一.连续性倒塌工况下钢管柱框架节点的破坏模式与鲁棒性[J].建筑结构学报,2015,36(4):9-15.LI Ling,WANG Wei,CHEN Yiyi.Failure modes and robustness of beam-to-column joints for steel tubular frame resisting progressive collapse[J].Journal of Building Structures,2015,36(4): 9-15.
[2]YANG B,TAN K H.Experimental tests of different types of bolted steel beam-column joints under a central-column removal scenario[J].Engineering Structures,2013,54(9): 112-130.
[3]谢甫哲,舒赣平.空间钢框架连续倒塌拟静力试验[J].解放军理工大学学报(自然科学版),2013,14(2):195-201.XIE Fuzhe,SHU Ganping.Quasi-static experimental re-search on progressive collapse of space steel frames[J].Journal of PLA University and Technology (Natural Science Edition),2013,14(2): 195-201.
[4]霍静思,王宁,陈英.钢框架焊接梁柱节点子结构抗倒塌性能试验研究[J].建筑结构学报,2014,35(4):100-108.HUO Jingsi,WANG Ning,CHEN Ying.Experimental study on collapse resistance of welded beam-column connection substructure of steel frame based on seismic design[J].Journal of Building Structures,2014,35(4):100-108.
[5]王开强,李国强,杨涛春.考虑悬链线效应的约束钢梁在分布荷载作用下的性能(I)—理论模型[J].土木工程学报,2010,43(1): 1-7.WANG Kaiqiang,LI Guoqiang,YANG Taochun.A study of restrained steel beams with catenary action under distributed load—Part I: theoretical model[J].China Civil Engineering Journal,2010,43(1): 1-7.
[6]郑阳,邹道勤,杨涛.基于悬链线理论的钢结构抗连续倒塌分析[J].钢结构,2012,27(163): 10-15.ZHENG Yang,ZOU Daoqin,YANG Tao.Analysis of resist progressive collapse for steel structure based on the theory of catenary action[J].Steel Constructure,2012,27(163): 10-15.
[7]何政.框架结构悬链线效应研究新进展[J].力学进展,2012,42(5): 47-561.HE Zheng.Progress in studies of catenary action in frame structures[J].Advances in Mechanics,2012,42(5):547-561.
[8]GUO L H,GAO S,FU F,et al.Experimental study and numerical analysis of progressive collapse resistance of composite frames[J].Journal of Constructional Steel Research,2013,89: 236-251.
[9]KANDIL K S,ELLOBODY E A,ELDEHEMY H.Progressive collapse of steel frames[J].World Journal of Engineering and Technology,2013,1: 39-48.
[10]杨卫忠,王茜.钢框架梁柱节点平齐式端板连接的数值分析[J].四川建筑科学研究,2013,39(4): 39-42.YANG Weizhong,WANG Qian.Numerical analysis of flush endplate connections in steel frames[J].Sichuan Building Science,2013,39(4): 39-42.
[11]GSA.Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects: GSA 2003[S].Washington,D.C.: United States General Services Administration,2003.
[12]石文龙.平齐端板连接半刚性梁柱组合节点的试验与理论研究[D].上海: 同济大学,2006.SHI Wenlong.Experimental and theoretical study on semi-rigid beam to column composite joints with flush endplate connection[D].Shanghai: Tongji University,2006.
[13]楼国彪,李国强,雷青.钢结构高强度螺栓端板连接研究现状[J].建筑钢结构进展,2006,8(2): 8-21.LOU Guobiao,LI Guoqiang,LEI Qing.Recent development in the behavior and design of high strength bolted endplate connections[J].Progress Steel Building Structures,2006,8(2): 8-21.
[14]British Standards Institution.Euro-code 3: design of steel structures.Part 1-8: design of joints,BS EN 1993-1-8:2005[S].UK: British Standards Institution,2005.
[15]ARASH N,FEREIDOON I.Progressive collapse analysis of steel frames: simplified procedure and explicit expression for dynamic increase factor[J].International Journal of Steel Structures,2012,12(4): 537-549.
[16]邓景龙,顾强.弯矩和轴力共同作用下梁柱平齐端板连接的弯矩-转角关系[J].苏州科技学院学报,2010,4(23): 26-30.DENG Jinglong,GU Qiang.Moment-Rotation relationship for beam-column flush endplate connection under bending moment and axial tension[J].Journal of Suzhou University of Science and Technology,2010,4(23):26-30.
[17]STYLIANIDIS P M,NETHERCOT D A.Modeling of connection behavior for progressive collapse analysis[J].Journal of Constructional Steel Research,2015,113: 1 69-184.
[18]YANG B,TAN K H.Numerical analyses of steel beam-column joints subjected to catenary action[J].Journal of Constructional Steel Research,2012,70(3):1-11.
