碳原子辐照损伤后石墨烯拉伸力学性能的温度相关性研究

李东波，赵 冬，华 军

(西安建筑科技大学理学院，陕西 西安 710055）

2004年，英国曼彻斯特大学的Geim等[1]利用机械剥离法首次制备并观察到单层石墨烯（Graphene），开启了石墨烯材料的研究热潮.石墨烯是由碳原子以sp2杂化轨道组成，具有六边形晶格构成的呈蜂巢状结构的二维纳米材料(图1)，这种特殊的结构赋予其超乎寻常的热学、力学和电学等性能，被誉为是具有战略意义的新材料，近年来迅速成为材料科学和凝聚态物理领域最为活跃的研究前沿[2-3].

图1 石墨烯原子结构示意图Fig.1 Graphene atomic structure diagram

温度对材料的性能具有重要影响，从热力学的角度而言，温度的变化会使得原子动能发生改变，从而对材料的稳定性和力学性能等产生影响，因此，对不同温度下材料性能的研究具有重要意义.但是，对于高（低）温等极限条件下材料性能的研究而言，实验操作难易控制，重复性较差，成本昂贵；相比而言，分子动力学等数值模拟方法在研究微观尺度下温度对材料性能的影响方面具有不可替代的优势.如Ni等[4]在室温（T=300 K）条件下分析了石墨烯拉伸性能的尺寸效应.Xiao等[5]用分子动力学方法研究了含缺陷石墨烯的拉伸性能.韩同伟等[6]采用分子动力学数值模拟方法研究了完美石墨烯拉伸力学性能的温度相关性，认为石墨烯力学性能的各向异性受温度影响较大.黄凌燕等[7]通过分子动力学方法研究了完美石墨烯拉伸力学性能的温度效应.

在石墨烯的应用方面，原子辐照技术已成为石墨烯加工和改性的重要手段，但由于辐照过程中入射粒子的随机性，会不可避免地给石墨烯造成损伤，因此，对辐照损伤后石墨烯的力学性能进行研究具有重要的科学意义和实用价值.

目前，对辐照损伤后石墨烯拉伸力学性能的温度相关性研究较少.为此，本文采用分子动力学方法，创建了碳原子辐照石墨烯及辐照损伤后拉伸的数值模型，对碳原子辐照损伤后石墨烯拉伸力学性能的温度相关性进行研究，揭示纳观尺度下温度对辐照损伤后石墨烯拉伸力学性能的影响.

1 数值模拟方法

本文采用分子动力学模拟软件LAMMPS(Large-scale Atomic/Molecular Massively Parallel Simulator)创建了碳原子辐照石墨烯和辐照损伤后石墨烯拉伸的数值模型，所建模型大小为 8.30 nm×8.36 nm，共包含2 760个原子.

1.1 辐照数值模型

辐照模型中，入射粒子初始位置位于模型上方一定高度，然后以一定角度和速度随机入射到模型上，通过入射原子和石墨烯原子的碰撞，实现对模型的辐照，如图2所示.

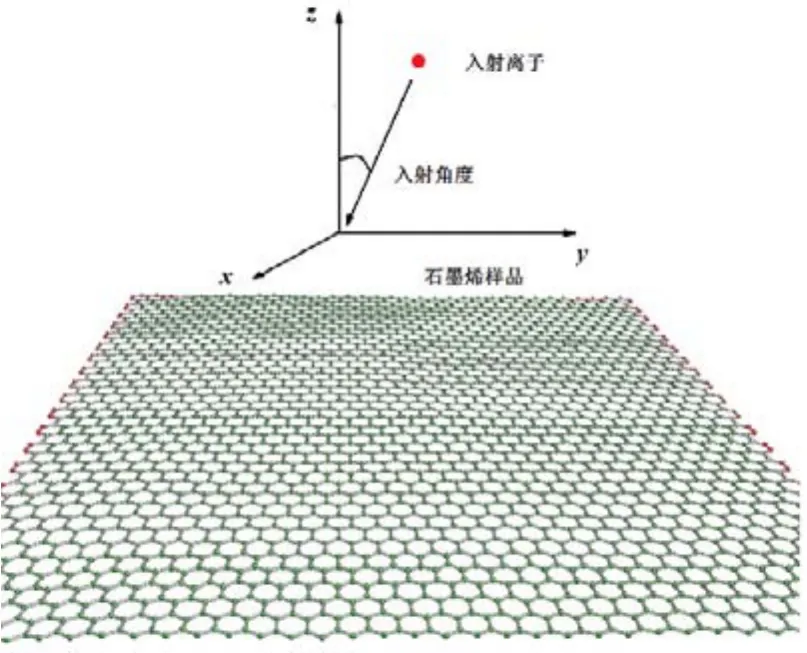
图2 原子辐照石墨烯原子构型图Fig.2 Atomic configuration diagram of graphene irradiated by C atoms

本文设定碳原子从6 nm高度垂直入射30个，每个粒子入射能量为1 kev.石墨烯内碳原子间的相互作用采用AI-REBO势函数[8]，该函数是对REBO势的改进和推广，增加了长程相互作用项和扭曲项，能准确描述石墨烯、碳纳米管等碳原子间的相互作用，其势能函数表达式为：

在辐照过程中，每入射完一个粒子后，将模型驰豫1 ps使其温度回复至初始设定温度，然后再进行下一个粒子的入射.由于入射碳原子和石墨烯靶原子之间的相互碰撞，辐照后会在石墨烯形成多个空位缺陷，从而造成对石墨烯的损伤，如图3所示.

现在各类跨境电商比赛很多。要想通过比赛促进跨境电商专业教学，比赛绝不能脱离跨境电商岗位实际。学生参加的跨境电商比赛至少要有网店开设、网店产品发布、网店装修、网店运营与营销策划推广、网店客户服务与管理及跨境电商物流等跨境电商必有的几个任务模块。

图3 辐照损伤后的石墨烯原子构型图Fig.3 Atomic configuration diagram of graphene with irradiated defects

1.2 拉伸数值模型

辐照完成后，以辐照损伤后的石墨烯为对象，采用分子动力学方法模拟其在0K、300 K、600 K、900 K、1 200 K、1 500 K、1 800 K、2 100 K、2 400 K、2 700 K和3 000 K等条件下的拉伸破坏过程，从而得出温度对其拉伸力学性能的影响.

在所建拉伸模型中，石墨烯的面内方向(x、y)设为周期性边界条件，时间步长设为1 fs.选用AIREBO势函数描述碳原子间相互作用，该势函数默认的转换函数参数介于1.7～2.0之间，但以往研究表明[12-13]，用该势函数描述碳纳米管、石墨烯等碳基材料的拉伸断裂时，当C-C键键长超过1.7A˙时，会引起与物理常识不符的断裂应力的升高现象.因此，为避免该现象的发生，本文将AIREBO势函数中的转换函数参数设为2.0.

拉伸时，先将模型在恒温恒压(NPT)系综下弛豫10 ps，然后在正则系综(NVT)下，将模型两端一层碳环的碳原子分别沿x或y方向施加均匀拉伸应变.每次加载后弛豫1 ps，重复此拉伸、弛豫过程，直至石墨烯被拉伸断裂.

2 结果分析

根据分子动力学数值模拟结果，可得辐照损伤后石墨烯在不同温度下（0 ～3 000 K）的拉伸应力-应变曲线，如图4所示.

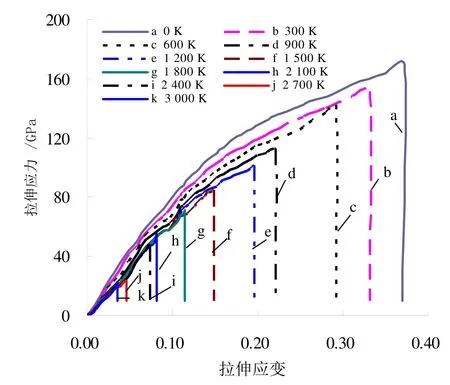
图4 不同温度下辐照损伤后石墨烯拉伸应力-应变曲线Fig.4 Tensile stress - strain curve of graphene after irradiation damage under different temperature

由图可见，与完美石墨烯相比，辐照损伤后石墨烯在拉伸的初始阶段（应变为0～0.02）表现出较强的非线性，且温度越高，非线性趋势越明显.分析认为，这是因为辐照损伤后多个空位缺陷的存在使得弛豫后石墨烯褶皱程度增大并分布不均，且温度越高，褶皱程度及分布不均匀程度越大，致使在外荷载作用下，力和变形之间的非线性愈加明显，从而使得拉伸初始阶段的应变-应变曲线表现出较强的非线性.

对完美石墨烯而言，前期研究[7]一般取应力-应变曲线中应变0～0.04段的曲线进行拟合后得到拉伸弹性模量.但对辐照损伤后的石墨烯而言，如上文所述，初始阶段的应力-应变曲线呈现较强的非线性.因此，本文取图4应力-应变曲线中应变在0.02～0.04段进行最小二乘法拟合，得到辐照损伤后石墨烯的弹性模量；且由图4可得石墨烯辐照损伤后的极拉伸强度、拉伸极限应变等弹性参量，见表1.

表1 不同温度下，辐照损伤后石墨烯的拉伸力学参量Tab.1 Tensile mechanical parameters of graphene after irradiation damage under different temperature

为研究辐照损伤后石墨烯拉伸力学性能随温度变化情况，根据表1可得不同温度下，辐照损伤后石墨烯弹性模量、拉伸强度和极限应变等拉伸力学性能随温度变化趋势图，如图5所示.

图5 辐照损伤后石墨烯拉伸力学性能随温度变化趋势图Fig.5 Tensile mechanical parameters changing trend chart of grapheme after irradiation damage with temperature

由图5(a)可见，当温度从0 K升高至3 000 K时，完美石墨烯和原子辐照损伤后石墨烯的杨氏模量均随温度升高而减小，但相比而言，辐照损伤后的石墨烯从0.922 TPa降至0.665 TPa，降幅达30.59%，而完美石墨烯的弹性模量的降幅为24.32%.由图5(b)可见，当温度从0 K升高至3 000K时，原子辐照损伤后的拉伸强度从159.68 GPa降至59.63 GPa，降低幅度为62.67%，完美石墨烯的拉伸强度降幅为43.41%.由图5(c)可见，当温度从0 K升高至3 000 K时，辐照损伤石墨烯的拉伸极限应变从0.383降至0.154，降低幅度为57.59%，完美石墨烯的极限拉伸应变降低幅度为41.25%.

3 辐照损伤后石墨烯拉伸力学性能温度相关性分析

由前所述，相比于完美石墨烯，辐照损伤后石墨烯的拉伸力学性能具有更强的温度相关性.根据统计热力学理论，系统所有原子的动能与温度一般满足以下关系式[6]：

式中：Ek为系统总动能；N为系统总原子数；kB为波尔兹曼常数；T为系统的热力学温度.由式（2）可知，随温度的升高系统的总动能增大，从而造成高温时系统内部原子的热运动愈加剧烈，致使原子在其平衡位置的振动幅度增大，从而导致系统中原子间相互吸引力相对减小，原子更容易克服束缚能并脱离固有的平衡位置而失稳，在原子点阵内部形成微小缺陷，当承受外载时，会造成点阵缺陷的扩展，并贯通造成材料的断裂，致使材料力学性能的下降.

同样，对于石墨烯而言，其在非绝对零度条件下时，体系中的碳原子总是以其平衡位置为中心进行热振动.当温度较低时，体系的动能较小，原子的自振幅度较小，原子难以克服体系束缚能，原子脱离平衡位置形成缺陷的几率较小.随着温度升高，体系的动能增大，原子自振幅度增大，当原子的能量超过体系原子对其的束缚时，即脱离平衡位置，形成点缺陷，且温度越高，缺陷形成的机会就越多，扩展速度越快，石墨烯越容易被拉断，从而造成石墨烯力学性能的下降.

对于辐照损伤后的石墨烯而言，由于辐照损伤造成大量空位缺陷的存在，使得石墨烯模型中存在较多的不完全成键碳原子，这些碳原子本身处于一种“激活状态”，点阵束缚能低，自身稳定性较差，使得其在温度升高时，随着动能的增大，更易超过体系束缚能的约束而脱离平衡位置，形成更大范围的缺陷，此时，当受到外载的扰动时，缺陷极易扩展、贯通，从而造成拉伸力学性能的降低.

4 结论

本文基于MD数值模拟，分析了碳原子辐照损伤后石墨烯弹性模量、拉伸强度和极限应变等拉伸力学性能的温度相关性，主要结论包括：

(1)当温度从0 K升高至3 000 K时，辐照损伤后的石墨烯从0.922 TPa降至0.665 TPa，降幅达30.59%，而完美石墨烯的弹性模量的降幅为24.32%.

(2)当温度从0 K升高至3 000 K时，原子辐照损伤后的拉伸强度从159.68 GPa降至59.63 GPa，降低幅度为62.67%，完美石墨烯的拉伸强度降幅为43.41%.

(3)当温度从0 K升高至3 000 K时，辐照损伤石墨烯的拉伸极限应变从0.383降至0.154，降低幅度为57.59%，完美石墨烯的极限拉伸应变降低幅度为41.25%.

(4)相对于完美石墨烯，辐照损伤后石墨烯的拉伸力学性能对温度的变化更加敏感.

(5)相比而言，拉伸极限强度对温度变化的敏感性最强，其次是拉伸极限应变，最后是弹性模量.

References

[1]GEIM A K,NOVOSELOV K S.The rise of graphene[J].Nature Material,2007,6(3): 183-191.

[2]韩同伟,贺鹏飞.石墨烯力学性能研究进展[J].力学进展,2011,41(3): 279-292.HAN Tongwei,HE Pengfei.Research progress in the mechanical properties of graphene[J].Advances In Mechanics,2011,41(3): 279-292.

[3]Brink J van den.Graphene: from strength to strength[J].Nature Nanotechnology,2007,2(4): 199-201.

[4]NI Z H,BU H,ZOU M,et,al.Anisotropic mechanical properties of graphene sheets from molecular dynamics[J].Physica B,2010,405: 1301-1306.

[5]XIAO J R,STANISZEWSKI J,GILLESPIE Jr J W.Tensile behaviors of graphene sheets and carbon nanotubes with multiple Stone-Wales defects[J].Mater Sci Eng A,2010,527: 715-723.

[6]韩同伟,贺鹏飞,王健,等.石墨烯拉伸力学性能温度相关性的数值模拟[J].同济大学学报(自然科学版),2009,37(12): 1638-1641.HAN Tongweil,HE Pengfeil,WANG Jian,et al.Numerical simulation of temperature dependence of tensile mechanical properties for single Graphene sheet[J].Jounal of Tongji University(Natural Science),2009,37(12):1638-1641.

[7]黄凌燕,韩强.单层石墨烯温度效应的分子动力学模拟[J].中国科学: 物理学·力学·天文学,2012,42(3):319-326.HUANG Lingyan,HAN Qiang.Molecular dynamics simulation of temperature effect on mono-layer graphene sheets[J].Scientia Siinica Physica,Mechanica &Astronomica,2012,42(3): 319-326.

[8]STUART S J,TUTEIN A B,HARRISON J A.A reactive potential for hydrocarbons with intermolecular interactions[J].J Chem Phys,2000,112(14): 6472-86.

[9]TERSOFF J.New empirical approach for the structureand energy of covalent systems[J].Phys Rev B,1988,37:6991.

[10]ZIEGLER J F,BIERSACK J P,LITTMARK U.Stopping andranges of ions in matter[M].New York: Pergamon,1985.

[11]梁力,赵仕俊,王宇钢,等.重粒子辐照下石墨烯力学性能的分子动力学研究[J].北京大学学报(自然科学版),2013,49(3): 365-370.LIANG Li,ZHAO Shijun,WANG Yugang,et al.Atomistic simulation of mechanical properties of graphene under heavy ion irradiation[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2013,49(3): 365-370.

[12]PEI Q X,ZHANG Y W,SHENOY V B.A molecular dynamics study of the mechanical properties of hydrogen functionalized graphene[J].Carbon,2010,48(3): 898-904.

[13]SHENDEROVA O A,BRENNER D W,OMELTCHENKO A,et al.Atomistic modeling of the fracture of polycrystalline diamond[J].Phys Rev B,2000,61(6): 3877-88.