Winkler弹性地基板梁的自由振动分析①

Winkler弹性地基板梁的自由振动分析①

通信作者：蒋吉清。E-mail：jiangjq@zucc.edu.cn。

魏纲1， 李钢2， 蒋吉清1， 魏新江1

(1.浙江大学城市学院工程分院，浙江 杭州 310015； 2.浙江大学建筑工程学院，浙江 杭州 310058)

摘要：中短型轨道板的几何构型介于梁、板之间，属于宽梁结构。从Mindlin板理论出发，退化得到适用于宽梁的Mindlin板梁控制方程；引入Winkler地基刚度系数，推导得到位移和转角的模态函数表达式。考虑两端简支的边界条件，得到弹性地基板梁的自由振动特征方程。通过无量纲数值算例求解出弹性地基板梁的自振频率，并与Timoshenko梁理论和Mindlin板理论进行对比。研究高跨比、泊松比和弹性地基刚度等参数对结构自振特性的影响，总结出弹性地基板梁方程的特点及适用范围，即宽度效应显著且泊松比较大的宽梁结构。

关键词：Winkler地基； Mindlin板梁； 自振频率； 泊松比

收稿日期：①2014-08-20

基金项目：国家自然科学基金(51278463，11202186)；浙江省自然科学基金(LQ12E08009)

作者简介：魏纲(1977-)，男，博士，教授，主要从事软土地基处理和地下隧道结构相关的教学和科研。E-mail：weig@zucc.edu.cn。

中图分类号:TU311.3文献标志码：A

DOI:10.3969/j.issn.1000-0844.2015.03.0655

Free Vibration Analysis of a Mindlin Plate-beam

on a Winkler Elastic Foundation

WEI Gang1, LI Gang2, JIANG Ji-qing1, WEI Xin-jiang1

(1.SchoolofEngineering,ZhejiangUniversityCityCollege,Hangzhou310015,Zhejiang，China;

2.CollegeofCivilEngineeringandArchitecture,ZhejiangUniversity,Hangzhou310058,Zhejiang，China)

Abstract：In recent years, short- and medium-length floating-slab tracks have become commonly used in railway engineering. These tracks are of a model type between a Winkler foundation beam and a Winkler foundation plate. For this type of wide-beam structure, a more suitable theory is required that both ensures calculation accuracy, as does the plate theory but also provides a simple analytical process, such as that of beam equations. In this study, the governing equations of the Mindlin plate are degraded and the dynamic equations for wide-beam structures are obtained: this is called the Mindlin plate-beam theory. Although the equations of the Mindlin plate-beam theory appear similar to the equations of the Timoshenko beam theory, the coefficient of bending stiffness is different and retains the direct influence of the Poisson's ratio parameters. This means that lateral deformation can be considered in the Mindlin plate-beam theory. The stiffness of the elastic foundation is also considered, and the equations are extended accordingly. For general analysis, the variables and parameters in this study are normalized and the expressions for both the vertical displacement and flexural rotation angle of a wide beam are obtained. Based on the boundary conditions, the dynamic characteristic equation for a simply supported wide beam is finally derived, and the normalized frequencies for the wide beam can be calculated through certain root searching programs. In this study, different kinds of boundary conditions are considered using the same procedure. To illustrate the wide-beam theory described herein, several numerical examples are used and the natural frequencies of a Mindlin plate-beam on a Winkler elastic foundation are compared with the results of a Timoshenko elastic foundation beam and a Mindlin elastic foundation plate. The results demonstrate the accuracy of the present equations. The effects of the height-to-length Poisson's ratios and elastic foundation stiffness are considered and the following conclusions are obtained from the numerical results: (1) For a simply supported wide beam, the first three frequencies of the plate-beam model show good agreement with those based on the Mindlin plate model. The discrepancy of the results from the two beam models increases with the width of the beam as compared to those of the Mindlin plate. However, the fundamental frequency of the Mindlin plate-beam theory still remains in good agreement with the plate theory; (2) the natural frequencies obtained from the Mindlin plate and Mindlin plate-beam theories will increase with the Poisson's ratio for a wide beam on an elastic foundation and those obtained from the Timoshenko beam theory will decrease. This result means that the relative error of the beam-plate and Mindlin plate will further reduce for a larger Poisson's ratio; and (3) the equations derived here are suitable for wide-beam analysis, can incorporate the effect of beam width, and are especially suitable for a wide foundation beam with a relatively large Poisson's ratio. The numerical examples based on this approximation theory are in good agreement with the Mindlin plate theory, while the equations and calculation process are much simpler.

Key words： Winkler foundation; Mindlin plate-beam; natural frequency; Poisson's ratio

0引言

梁和板是土木工程常用的结构形式，其相关的力学问题一直是学者研究的热点[1-3]。工程中常用的梁理论有Euler梁和Timoshenko梁两类，板理论则有Kirchhoff板和Mindlin板等。相对而言，Timoshenko梁和Mindlin板在中厚结构及中高频动力分析方面更具优越性。有学者采用Timoshenko梁对Mindlin板进行退化分析[4]，但在退化过程中却未能考虑Timoshenko梁在结构宽度方向上的尺寸效应。

弹性地基上的梁和板振动是工程领域广泛关注的重要问题之一。吕朝锋[5]基于二维平面理论和状态空间微积分法分析了Winkler弹性地基梁的自由振动。Wang等[6]采用Green函数给出了弹性地基Timoshenko梁在不同参数条件下的静动力解析解。Akhavan等[7]推导出了面内受荷时的Mindlin板在Winkler地基上的精确解。Xiang[8]分析了Mindlin板在分段不均匀弹性地基上的振动。

现在铁路工程上常用的板式轨道，尤其是弹性CA砂浆板式轨道[9]和橡胶垫浮置板轨道[10]，其构件模型介于Winkler地基梁和Winkler地基板之间。对于这种宽梁结构，当前的研究大多集中在工程应用的角度，少有理论方面的讨论。有必要寻求一种合适的计算理论，既能得到类似于板理论的计算精度，又能保证其分析过程如梁方程般简洁。为此，Mindlin本人从Mindlin板的控制方程出发，退化得到适用于宽梁结构的动力方程[13]。本文将此退化方程整理并定义为Mindlin板梁方程(Mindlin Plate-beam theory，简称P-B方程)，并在方程中考虑弹性地基刚度的影响；通过数值算例分析Winkler地基上的Mindlin板梁的固有频率，分别与Timoshenko弹性地基梁、Mindlin弹性地基板的计算结果进行对比，由此验证本文方程。

1Mindlin弹性地基板梁的动力方程

根据Mindlin板的动力控制方程[10]，并假设转角ψx和竖向挠度υ沿z方向保持不变，即ψx=ψx(x,t)，υ=υ(x,t)；同时，忽略绕y轴转角ψz的影响，即可退化得到如下方程[12]

式中：E和G分别为弹性模量和剪切模量；ρ为材料密度;κ=π2/12为剪切系数;I是关于z轴的转动惯量；A为横截面面积；b为截面宽度;q为分布荷载；D=Eh3/12(1-μ2),为抗弯刚度系数；h为板厚;μ为泊松比。位移υ和转角ψx的正方向如图1所示。

图1　板梁模型示意图 Fig.1　Sketch of the plate-beam model

式(1)为适用于宽梁结构的Mindlin板梁方程，由Mindlin本人首先提出,该方程与Timoshenko梁方程非常相近，但抗弯刚度系数有所区别，并保留了泊松比参数的直接影响，若考虑弹性地基的影响，式(1)将变为

式中：Kw为Winkler地基刚度。

2弹性地基板梁的自由振动分析

对于单根均匀弹性地基板梁，当不考虑外力作用，即q(x,t)=0时，板梁处于自由振动状态。根据分离变量法的思路，分别令υ(x,t)=V(x)eiωt，ψx(x,t)= ψ(x)eiωt，代入式(2)并消去eiωt可得

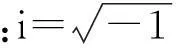
对于两端简支的弹性地基板梁，无量纲后的边界条件可整理为：

将式(6)和(7)代入，并整理成矩阵形式：

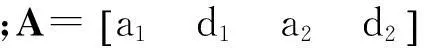
3数值算例及分析

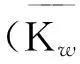
表1给出了不同地基刚度下三种计算理论得到的前三阶无量纲频率系数ϖ。从中可以看到，不论是高跨比很小的浅梁(λ=1/100)、高跨比较大的深梁(λ=1/10)，还是更极端的矩形中厚板(λ=3/10)，板梁理论的结果总体上更接近二维Mindlin中厚板理论。

表1说明，在浅梁范畴(λ=1/100)，也就是长度方向的尺寸远大于宽度和厚度时，虽然板梁理论的结果与Mindlin板理论更为接近，但Timoshenko梁理论与Mindlin板的最大误差也仅为0.73%，且随着地基刚度的增加误差还在进一步降低。可见，在高跨比很小的浅梁范畴，采用Timoshenko梁理论，甚至是经典梁理论，都是可行的。

对于λ=1/10的深扁平梁，相比较Timoshenko梁的计算结果，板梁与Mindlin板理论更为接近。此时Timoshenko梁与Mindlin板的最大误差增大近4倍，达到2.46%。随着地基刚度的增加，误差虽有所降低，但降低幅度不大。因此，对于较大高跨比的宽梁，板梁理论的计算结果相对于Timoshenko梁更接近实际，体现出板梁在宽扁梁到中厚单向板范围内的优越性。

表 1　前三阶固有频率系数ϖ的比较

针对λ=3/10且b/h=2的矩形中厚板，此时长宽高基本在一个量级范围内。从计算结果看出:板梁理论得到的值与Mindlin板理论虽然更为接近，但也仅限于低阶;在第三阶时，两种梁理论与Mindlin板理论的最大误差都超过10%，随着地基刚度的增加，误差有所降低。因此，双向矩形板范围内板梁理论在低阶频率求解时能体现一定的优越性，但总体上看此时用梁理论来近似模拟已不合理。

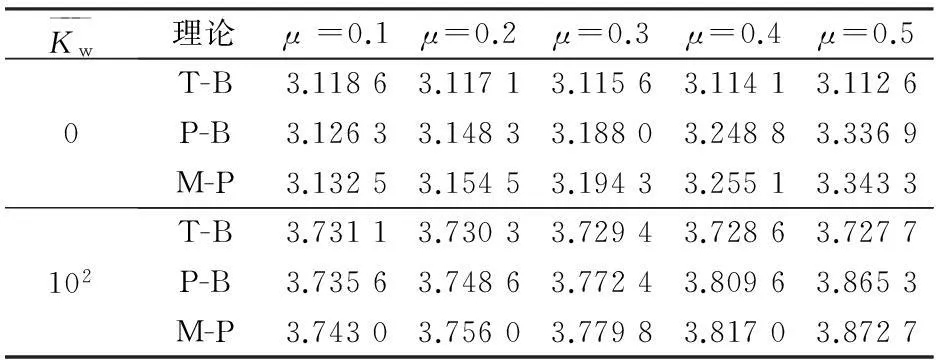
表 2　不同泊松比下三种理论的基频系数比较( λ=1/10)

除了考虑结构尺寸的影响，还考察了三类理论在不同泊松比取值下的首阶频率系数随地基刚度的变化情况。该结果基于b/h=2且λ=1/10的深扁平梁模型，同时也是板梁最佳的适用范围。如图2所示，在不同地基刚度下，随泊松比的增加板梁的基频增高，体现出与Mindlin板相同的趋势。但是Timoshenko梁的变化趋势却刚好相反，即随泊松比的增加，固有频率有小幅度的下降。由此可以得出，对于泊松比较大的材料，采用板梁理论分析弹性地基宽梁结构的动力性能更加精确，也再次反映出板梁理论能够考虑宽度变形效应的影响。

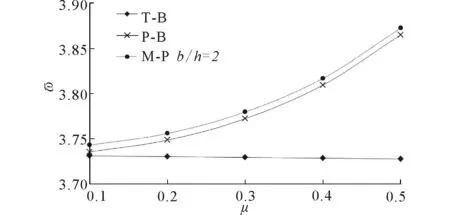
图2　不同泊松比下三种理论基频系数比较 　　　 ( ——=100) Fig.2　Comparison of the fundameratal frequency 　　　 coefficients based on three theories 　　　 with different Poisson’s ratios ( =100)

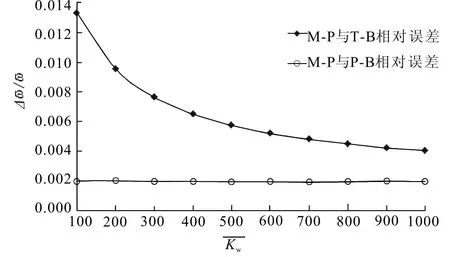
图3　不同理论基频随地基刚度变化误差 Fig.3　Comparison of the fundamental frequency 　　　 coefficients based on three theories 　　　 with different foundation stiffness

以Mindlin板为基准，分别考察不同地基刚度下板梁理论和Timoshenko梁理论的首阶自振频率系数相对误差。如图3所示，随着地基刚度的增加，板梁与Mindlin板的相对误差较为稳定，且相对较小;而Timoshenko梁与Mindlin板的相对误差稍大，但随着地基刚度的增加呈现减小的趋势。

4结语

分析由Mindlin板理论退化得到的板梁控制方程在Winkler地基上的自振特性，得到以下结论：

(1) 简支边界条件下，在通常的中长梁范围内，较之Timoshenko梁，弹性地基上的板梁与Mindlin板的前三阶振动频率更加吻合，且随着板宽的增加，低阶频率同样吻合良好。

(2) 随泊松比的增加，弹性地基板梁的自振频率趋势及计算精度与Mindlin弹性地基板更加一致，当地基刚度增加时板梁与Mindlin板的相对误差将进一步降低。

(3) 本文方程适用于宽度效应显著(b/h≤4)、泊松比较大的Winkler地基宽扁梁结构，且在保证近似于Mindlin板理论的精度情况下，可以避免复杂的运算过程。

参考文献(References)

[1]TimoshenkoSP.OntheCorrectionforShearoftheDifferentialEquationforTransverseVibrationsofPrismaticBars[J].PhilosophicalMagazine，1921，41(245)：744-746.

[2]TimoshenkoSP.VibrationProblemsinEngineering[M].NewYork:Wiley, 1974.

[3]ChakravertyS.VibrationofPlates[M].BocaRaton：CRCPress，2009.

[4]马晨明.Kirchhoff板和Mindlin板上动态分布荷载的辨识问题研究[D].上海：复旦大学, 2004.

MAChen-ming.ResearchonDeterminationofDynamicLoadDistributionAppliedtoKirchhoffPlatesandMindlinPlates[D].Shanghai:FudanUniversity, 2004.(inChinese)

[5]吕朝锋, 陈伟球, 边祖光. 状态空间微积分法分析Winkler地基梁的自由振动[J].浙江大学学报:工学版,2004, 38(11):1451-1454.,

LVChao-feng，CHENWei-qiu，BIANZu-guang.FreeVibrationAnalysisofBeamsonWinklerFoundationviaState-space-basedDifferentialQuadrature[J].JournalofZhejiangUniversity:EngineeringScience,2004，38(11)：1451-1454.(inChinese)

[6]WangCM，LamKY，HeXQ.ExactSolutionsforTimoshenkoBeamsonElasticFoundationsUsingGreen’sFunctions[J].MechanicsofStructureandMachines, 1998, 26(1)：101-113.

[7]AkhavanH，HosseiniHashemiSh，RokniDamavandiTaherH,etal.ExactSolutionsforRectangularMindlinPlatesUnderIn-planeLoadsRestingonPasternakElasticFoundation.PartII:FrequencyAnalysis[J].ComputationalMaterialsScience,2009,44：951-961.

[8]XiangY.VibrationofRectangularMindlinPlatesRestingonNon-homogenousElasticFoundations[J].InternationalJournalofMechanicalSciences，2003，45：1229-1244.

[9]左景奇，姜其斌，傅代正，等.板式轨道弹性垫层CA砂浆的研究[J].铁道建筑，2005，9：96-98.

ZUOJing-qi，JIANGQi-bin，FUDai-zheng，etal.StudyofCementAsphaltMotarIncludedinElasticPadUnderSlabTrack[J].RailwayEngineering，2005，9：96-98.(inChinese)

[10]耿传智, 楼梦麟. 浮置板轨道结构系统振动模态分析[J].同济大学学报：自然科学版，2006，34(9)：1201-1205.

GENGChuan-zhi，LOUMeng-lin.VibrationModelAnalysisofFloatingSlabTrackSystem[J].JournalofTongjiUniversity：NaturalScience,2006, 34(9)：1201-1205.(inChinese)

[11]MindlinRD.InfluenceofRotatoryInertiaandShearonFlexuralMotionsofIsotropic，ElasticPlates[J].JournalofAppliedMechanics，1951，18(1)：31-38.

[12]MindlinRD.Thickness-shearandFlexuralVibrationsofCrystalPlates[J].JournalofAppliedPhysics，1951，22(2)：316-323.

[13]CalimFF，AkkurtFG.StaticandFreeVibrationAnalysisofStraightandCircularBeamsonElasticFoundation[J].MechanicsResearchCommunications, 2011, 38(2):89-94.