混合动力汽车动力耦合行星齿轮系动力学模态

杨忠凯,廖连莹，2，左言言，倪明明

(1.江苏大学 振动噪声研究所,江苏 镇江 212013；2.常州工学院 机电工程学院，江苏 常州 213002)

混合动力汽车动力耦合行星齿轮系动力学模态

杨忠凯1,廖连莹1，2，左言言1，倪明明1

(1.江苏大学 振动噪声研究所,江苏 镇江 212013；2.常州工学院 机电工程学院，江苏 常州 213002)

摘要：以混合动力汽车双排行星齿轮动力耦合机构为例，运用UG建立其三维实体模型，并在ANSYS中对动力耦合机构的两排斜齿行星齿轮系分别进行模态分析。通过对比分析两排行星齿轮系的固有属性，得出两行星齿轮系的振动都以行星轮的扭转或扭摆振动为主，且由于存在重根现象，固有频率相近的模态，其固有振型也相似。两斜齿行星齿轮系的固有频率都远大于混合动力汽车发动机、发电机和电动机对外输出的激振频率。可见，斜齿行星齿轮系作为混合动力汽车动力耦合机构，能够有效地避免与动力输入构件的共振。

关键词：混合动力汽车；动力耦合机构；斜齿行星齿轮；模态分析

基金项目：教育部博士点基金项目(20103227110009);江苏省高校自然科学研究项目(13KJD460002)

作者简介：杨忠凯(1988-),男,山东聊城人,硕士生;左言言(1958-),男,江苏镇江人,教授,博士生导师,主要研究方向为车辆振动与噪声控制.

收稿日期：2014-09-13

文章编号：1672-6871(2015)02-0014-04

中图分类号：TH164

文献标志码：标志码：A

0引言

混合动力电动汽车至少拥有两种动力源，可以实现既不降低车辆动力性能，又可以降低油耗[1]。在实际应用中，混合动力汽车大都采用传统的内燃机、发电机/电动机作为动力源，而如何将各动力源输出的动力平稳地耦合在一起是混合动力汽车的最为关键技术之一[2-4]。目前，市场上主流的混合动力汽车主要采用行星齿轮动力耦合机构，但混合动力电动汽车在运行过程中要根据不同工况匹配策略进行各动力源之间的动力切换[5]，从而使动力耦合机构的工作环境也相当复杂。所以，对动力耦合机构中行星齿轮进行动力学分析显得尤为重要。

前人对行星齿轮动力学特性进行了大量的研究。文献[6-7]建立了直齿行星齿轮的纯扭转模型,并分析了行星齿轮系的固有特性。文献[8]通过考虑构件在径向平面内的平移振动，建立了直齿行星齿轮的平移—扭转耦合模型，研究其固有特性及行星齿轮参数变化对固有特性的影响。文献[9]建立了混合动力两级行星齿轮耦合系统的纯扭转动力学模型，并进行固有特性分析，按照振型特点把系统的振动形式划分为3种模式。文献[10]建立了行星齿轮的有限元模型，并与集中参数模型进行对比，发现两者的计算结果基本一致。

在前人研究的理论基础之上，本文采用有限元的方法，对某混合动力汽车动力耦合机构的行星齿轮系进行模态分析，重点分析行星齿轮系中各齿轮的振动特点，并对比分析了两排行星轮系的固有属性，探究行星齿轮系作为动力耦合机构关键部件的优越性。

1动力耦合机构三维实体建模

1.1　混联式混合动力系统

混联式混合动力系统综合了串联和并联的特点，其动力源包括内燃机系统和电机系统，通过行星齿轮动力耦合机构的耦合作用，既可以实现各动力源的单独驱动，也可以实现两动力源的共同驱动。本文以某混联式混合动力汽车为例，建立了其整个混合动力系统的传动示意图，如图1所示。

此混合动力系统的动力源包括发动机、发电机MG1/电动机MG2。其动力耦合机构由双排行星齿轮系构成，即动力分配行星齿轮排和电机减速行星齿轮排，两行星齿轮系都是2K-H型渐开线斜齿行星齿轮系，且都以齿圈作为动力输出构件，两排行星齿轮的齿圈分别嵌套在复合齿轮机构的左右两边。两行星齿轮系与各动力源的连接关系如下：

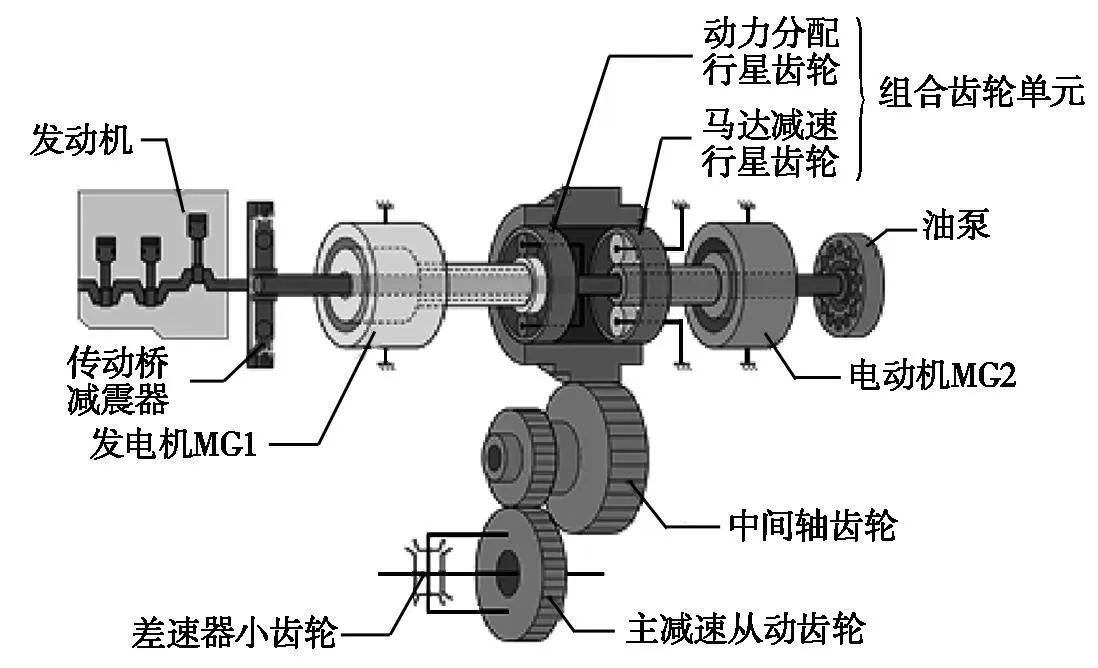
图1　某混联式混合动力系统结构示意图

(Ⅰ)动力分配行星齿轮排

行星架—发动机；

太阳轮—发电机MG1；

外齿圈—复合齿轮机构。

(Ⅱ)电机减速行星齿轮排

行星架—外部壳体；

太阳轮—电动机MG2；

外齿圈—复合齿轮机构。

1）断层。左岸断层以NWW向为主，其中断层F14、F17、F18规模较大，斜切水垫塘。其他断层规模较小。

1.2　动力耦合机构三维实体建模

常用的三维软件UG、Pro/E等都提供了专门的齿轮库，可以方便地对斜齿轮进行参数化建模。根据已知的结构参数，利用UG8.0自带的齿轮库建立行星轮系中各渐开线斜齿轮的实体模型，并在UG装配模块中进行动力耦合机构的实体装配，得到动力耦合机构三维模型，如图2a所示。表1即为两排行星齿轮各齿轮的基本参数，其中动力分配行星齿轮排包含4个行星轮，电机减速行星排包含5个行星轮[11]，如图2b所示。

图2　动力耦合机构的三维实体模型

表1　两行星齿轮排的齿轮参数

注：“前排”即动力分配行星齿轮排，“后排”即电机减速行星齿轮排。

2斜齿行星齿轮系有限元建模

由于主要研究行星齿轮系中各齿轮之间的相互作用，所以在进行有限元分析时，对两排行星齿轮都进行了相应的简化，忽略了行星架的影响；然后，在UG中以中间格式*step导出，再导入到ANSYS Workbench中进行前处理，创建有限元模型。两排行星齿轮采用的材料均为42CrMo，其密度DENS=7.85E+3 kg/m3，弹性模量E=2.12E+11 Pa，泊松比PRXY=0.28。

图3　行星齿轮系有限元模型

模态分析时，各斜齿轮之间的接触采用线性对称的Bonded接触。网格划分时，各齿轮轮齿部分采用10节点的四面体单元Solid187；轮体采用20节点的六面体单元Solid186；而对于Bonded接触对，Workbench会在接触对的接触面上生成8节点的高阶四边形接触单元Conta174，在目标面上生成三维目标单元Targe170[12]。划分的有限元模型如图3所示。

根据实际运行工况，分别对两排行星齿轮系施加如下约束：对太阳轮和行星轮内圆柱孔施加圆柱约束，约束其内圆柱孔的轴向和径向自由度，释放切向自由度；对齿圈外圆柱面施加圆柱约束，释放切向自由度[13]。

3斜齿行星齿轮系模态分析

3.1　斜齿行星齿轮系模态分析的基本原理

根据弹性动力学理论可以推导出行星齿轮传动系统的弹性动力学方程:

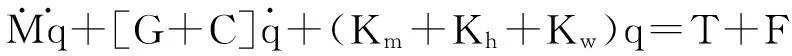
(1)

其中：M为质量矩阵；G为陀螺矩阵；C为阻尼矩阵；Km为啮合刚度矩阵；Kh为支撑刚度矩阵；Kw为向心刚度矩阵；q为位移矢量；T为输入转矩矢量；F为自激励力矢量。

对式(1)进行相应的简化，忽略与转速有关的陀螺矩阵G和向心刚度矩阵Kw[14]，在无阻尼、无外力的条件下得到系统的自由振动方程为：

(2)

与式(2)对应的特征方程为：

(3)

式中，ωi、φi(i=1,2,…,n)分别为系统的第i阶固有频率和固有振型。

3.2　动力分配行星齿轮排模态分析

图4　动力分配行星齿轮排部分振型图(单位：mm)

3.3　电机减速行星齿轮排模态分析

计算电机减速行星齿轮排的前30阶模态，其部分振型图如图5所示。

图5　电机减速行星齿轮排部分振型图(单位：mm)

通过对两排斜齿行星齿轮系的模态分析可知：

(Ⅰ)动力分配行星齿轮排最低阶固有频率为5.123 kHz，电机减速行星齿轮排最低阶固有频率为5.76 kHz，而四冲程直列四缸发动机、永磁同步电机对外输出的主要激振频率都远小于5 kHz。且两行星齿轮系的第1阶振型都表现为整体扭转振动，齿圈的振动最强烈，其他阶振动主要表现为行星轮的振动及齿圈的局部振动。

(Ⅱ)对于动力分配行星齿轮排，其第2、3阶固有频率都在10.11 kHz左右，它们对应的主振型皆为相对行星轮的扭转振动，如图4a和图4b所示；其第7、8阶固有频率为19.70 kHz左右，且主振型为相对行星轮绕其与齿圈捏合处的扭摆振动；还有第10阶、第11阶、第14阶、第15阶等都表现为固有频率相近，且固有振型相似。

(Ⅲ)对于电机减速行星齿轮排，其固有频率分布特点与动力分配行星齿轮排类似，即相近的固有频率对应的固有振型也相似，如图5所示。其第2、3阶固有频率都在9.45 kHz左右；第4、5阶固有频率都在13.79 kHz左右，它们的主振型都表现为3个行星轮的扭转振动；其第7、8阶固有频率都在19.65 kHz左右，主振型为部分行星轮的扭摆振动。

4结论

(1)两排行星齿轮系的固有频率远大于发动机、发电机/电动机对外输出激振频率，可见斜齿行星齿轮系作为混合动力汽车动力耦合机构，能够有效地避免与动力输入构件的共振。

(2)两排斜齿行星齿轮系的振动特性相似。其振动都以行星轮的扭转或扭摆振动为主，且固有频率相近的模态，其固有振型也相似。根据前人的研究可推知：相似的固有属性是由于行星齿轮系自由振动方程的解中存在重根现象，从而使得其固有频率相近，且固有振型相似。

参考文献：

[1]高建平,位跃辉,刘振楠.并联混合动力公交车动力系统匹配优化[J].河南科技大学学报:自然科学版,2014,35(1):30-35.

[2]薛峰.混合动力轿车用行星齿轮动力分配装置及整车仿真研究[D].上海:同济大学中德学院,2005.

[3]孙鹏龙,付主木,王周忠.并联式混合动力汽车再生制动控制策略[J].河南科技大学学报:自然科学版,2013,34(3):35-39.

[4]步曦,杜爱民.混合动力汽车用行星齿轮机构的理论研究与仿真分析[J].汽车工程,2006,28(9):834-853.

[5]高建平,李晓林,郭志军.改进型混合动力汽车工况预测算法的应用仿真[J].河南科技大学学报:自然科学版,2013,34(2):34-38.

[6]Kahraman A.Natural Modes of Planetary Geartrains[J].Journal of Sound and Vibration,1994,173(1):123-132.

[7]Kiracofe D R，Parker R G.Structured Vibration Modes of General Compound Planetary Gear Systems[J].Journal of Vibration and Acoustics,2007,129:1-16.

[8]Lin J,Parker R G.Analytical Characterization of the Unique Properties of Planetary Gear Free Vibration[J].Journal of Vibration and Acoustics,1999,121(7):316-321.

[9]罗玉涛,陈营生.混合动力两级行星机构动力耦合系统动力学建模及分析[J].机械工程学报,2012,48(5):70-75.

[10]Parker R G,Lin J.Modeling,Modal Properties and Mesh Stiffness Variation Instabilities of Planetary Gears[R].Washington D.C.:NASA,2001.

[11]Burress T A,Campbell S L,Coomer C L,et al.Evaluation of the 2010 Toyota Prius Hybrid Synergy Drive System[R].Oak Ridge,Tennessee:Oak Ridge National Laboratory,2011.

[12]凌桂龙,丁金滨,温正.ANSYS Workbench 13.0从入门到精通[M].北京:清华大学出版社,2012.

[13]白俊峰,王世杰,谢琨,等.渐开线斜齿行星轮系振动特性的模态分析[J].机械设计与制造,2013(10):206-208.

[14]杨通强,宋轶民,张策,等.斜齿行星齿轮系统自由振动特性分析[J].机械工程学报,2005,41(7):50-55.