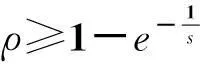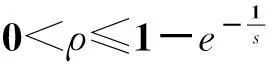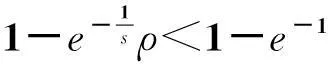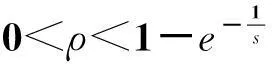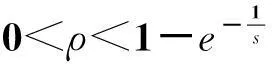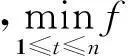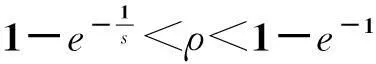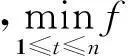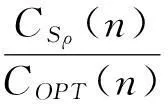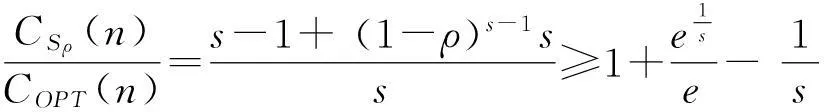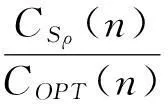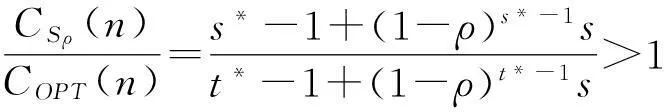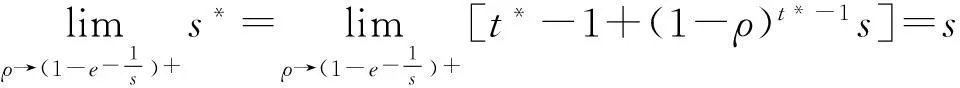购买价格递减的在线租赁问题策略设计

购买价格递减的在线租赁问题策略设计

胡茂林1，徐维军2

(1.淮阴师范学院数学科学学院运筹与优化研究室，江苏淮安223300；2.华南理工大学工商管理学院决策科学系，广东广州510641)

摘要：运用在线问题与竞争分析的方法研究了购买价格递减的在线租赁问题。通过揭示相关费用函数的性质，先后给出了最优离线策略以及在线策略。通过竞争比分析，证明了我们给出的在线策略是该问题唯一最优策略，而且该策略的竞争比随购买价格的优惠率的增加呈严格递减趋势。竞争分析结果表明考虑购买价格递减因素能够改进在线策略的竞争比从而提高决策效率。

关键词：在线租赁问题；在线策略；竞争分析；竞争比；购买价格递减

收稿日期：2012-12-24

基金项目：国家自然科学基金资助项目(71471065)；教育部人文社会科学研究规划基金(10YJA630062)；中央高校基本科研业务费专项资金资助(2012ZZ0035)

作者简介：胡茂林(1963-)，男，宁夏人，教授, 硕士生导师，研究方向：运筹与优化、在线金融算法；徐维军(1975-)，男，宁夏人，研究员，博士生导师，研究方向：管理科学与工程、在线金融算法。

中图分类号：F224.0 文章标识码：A

Strategy Design on Online Leasing Problem with Decreasing Purchasing Price

HU Mao-lin1, XU Wei-jun2

(1.SchoolofMathematicalScience,HuaiyinNormalUniversity,Huaian223300,China; 2.SchoolofBusinessAdministration,SouthChinaUniversityofTechnology,Guangzhou510641,China)

Abstract:In this paper, we use the method of competitive analysis for online problem to study an online leasing problem with decreasing price for purchasing. By analyzing the properties of cost functions concerned, the optimal offline strategy and an online strategy are given. By way of the analysis of competitive rate, we prove online strategy to be the unique optimal strategy for this problem, and competitive rate of this strategy is strictly decreasing with the preferential rate of purchasing price. The result shows that taking the factors of the decreasing of purchasing price will improve the competitive rate of online strategy and thereby increase the decision-making efficiency.

Key words:online leasing problem; online strategy; competitive analysis; competitive rate; decreasing purchasing price

0引言

租赁是社会经济活动中最常见的一种经济现象。关于租赁问题，经典的研究侧重于资产租赁合同分析及税收对租赁与购买决策的影响分析。到了1992年,Karp[1]提出了在理论计算机科学领域享有盛名的在线租雪橇问题：某滑雪者去滑雪场滑雪，在滑雪场每天租用一幅雪橇的租金为1，购买一幅雪橇的价格为s，一旦他在某一天买下一幅雪橇，则以后要滑雪时就不再付租用费。问滑雪者在不知道自己要滑多少天的情况下是租用雪橇还是购买雪橇或者是在租用多少天后再购买雪橇使得所花费用较少? 若滑雪天数已知则为离线问题，若滑雪天数未知则为在线问题。对于在线租雪橇问题，Karp证明了在租用s-1天后若要继续滑雪则立即购买雪橇最为划算。此时问题的竞争比为2-1/s。

随后在线问题之竞争分析的方法便成了研究租赁问题的热点方法。学者们在这一经典模型的基础上结合实际经济背景考虑了随机性算法，引入了利率，折旧，风险等因素得到了很多推广变形，涌现出了大量的关于在线租赁问题研究的文章。Karlin[2]等学者给出了在线租赁问题的随机性在线算法。El-Yaniv[3]等建立了设备更新模型，考察了资本市场上一个生产商更新设备问题，该模型可广泛地应用于供货商变更问题、菜单成本问题、融资抵押问题等。之后，El-Yaniv[4]又从实际经济决策角度出发，考虑了当投资者进行租赁活动时所面临的一个不可忽视的重要因素利率，给出了最优确定性算法和最优随机性算法。Irani和Ramanathan[5]研究了当购买价格波动而租赁费用保持不变情形，分别给出了确定性算法和随机性算法的竞争比上下界，并运用具有统计特征对手来研究在线租赁问题等。Azar[6]等考虑了生产商面对未知的需求订单和市场不断出现生产该商品的生产设备，生产商采取什么策略更新生产设备才能使得成本最小化问题。Fujiwara[7]等人结合未来输入具有连续性概率信息研究了在线租赁决策问题。Xu[8]等在Fujiwara研究的基础上，深入研究了存在利率情况下当输入的概率信息具有离散型结构的设备融资决策问题。在国内，王扬[9]、董玉成[10]等分别研究了有无利率情形下投资者具有各种预期的风险回报在线租赁问题等；胡茂林[11]考虑了连续可分资产的多重在线租赁问题；徐维军[12]等还考虑了购买价格和租金费用均连续可变的在线竞争策略分析问题，特别地，文中最后还提出了需要进一步研究的问题：当购买价格每期以固定比例呈现递减趋势变化时如何设计竞争策略。

虽然当购买价格递减变化时使在线租赁模型复杂化，但能获得更小的竞争比同时也是问题的研究向现实的一种贴近。正像文献[13]指出的那样，随着租赁业的快速发展，市场的激烈竞争,供求关系的不断变化，购买设备的价格也会不断发生变化。当供大于求时，租赁公司为了维持或者扩大业务量，经常会推出一些购买价格随租用时间的长短而给予优惠的措施或合同。

基于以上考虑，本文研究购买价格递减的在线租赁问题：设某用户或投资者要租用或购买某种设备进行生产。如果租用设备每个租用期的租金是1；如果购买设备，随着租用期数t的增加，购买价格等比例递减为(1-ρ)t-1s，即若在第一期购买则价格是s，若第一期租用再第二期购买则价格是(1-ρ)s，…… 若前n-1期租用到第n期购买则价格是(1-ρ)n-1s，0<ρ<1/e叫购买价格的优惠率。一旦投资者在某一期买下了设备就不必再付租用费。但投资者不知道自己将要使用这种设备多长时间，即使用期数t1,t2,…,tn是长度n不确定的租用期构成的时间序列。

如果ρ=0，则这一问题退化为Karp模型，因此我们考虑的购买价格递减的在线租赁问题是Karp模型的一种推广。

在本文中，像文献[4]等其它研究在线租赁问题的文献一样，我们约定s、t*和s*等参数都是正整数且s≥2。有关在线问题与在线算法的方法和术语我们参阅文献[13,14]。

1费用函数的性质

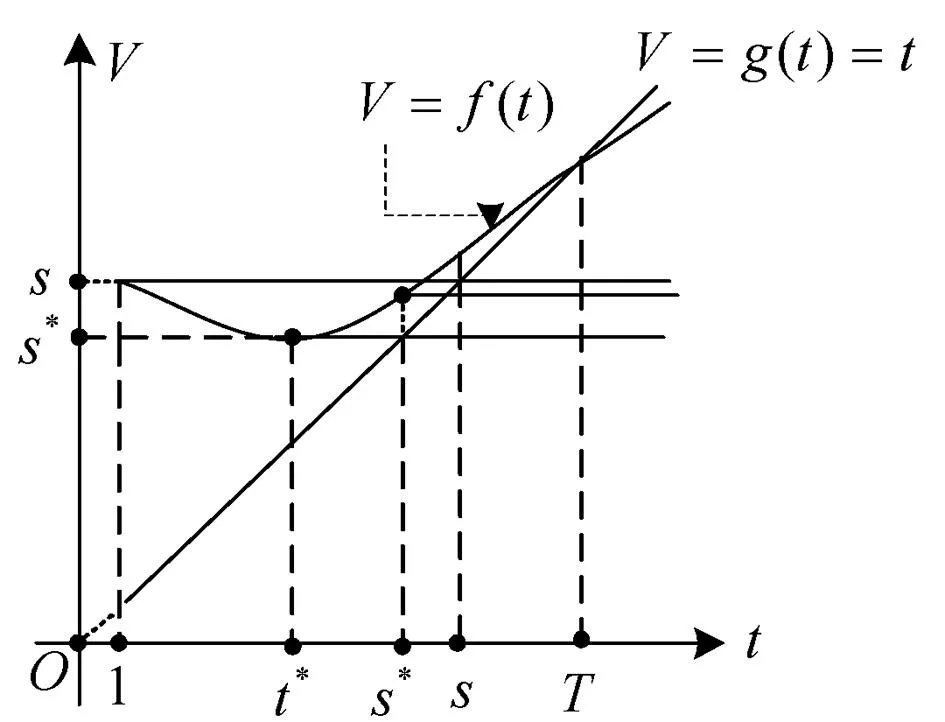
我们知道，对于原Karp在线租赁问题，无论投资者在租赁期内哪一期购买设备，购买价格恒为常数s；而且最优离线策略是当n

f(t)=t-1+(1-ρ)t-1s

(1)

与在租赁期内，从第一期租用设备直到t期结束所花费用的函数

g(t)=t

(2)

等费用函数的性质。这里1≤t≤n，并且先不妨假定优惠率0<ρ<1。

设F(t)=t-1+(1-ρ)t-1s-t，通过F(t)考察易知函数f(t)与g(t)在

(3)

处取得相等的函数值，并且当1≤tg(t)，当T

把(1)式对t求导并令其等于零得关于t的方程

f′(t)=1+(1-ρ)t-1sln(1-ρ)=0

(4)

解得其根

(5)

由于t*是方程(4)的根，所以

f″(t*)=(1-ρ)t*-1sln(1-ρ)·ln(1-ρ)=-ln(1-ρ)>0

因此，我们令

f(t*)=t*-1+(1-ρ)t*-1s

图1　当0< ρ≤1- 时费用函数的性态

图2　当1- < ρ<1- 时费用函数的性态

如果我们令s*=f(t*)，则有s*

把(5)式两边对ρ求导得

(6)

由(3)和(5)可知

(7)

2最优离线策略

虽然该问题所对应的离线问题的租赁时间序列t1,t2,…,tn的长度n是已知的，但最优离线策略与购买价格的优惠率密切相关。事实上，最优离线决策必然是根据已知n的大小分以下两种情况之一作出的：

(i)当n较小时，总是租用；(ii)当n较大时，租用t-1次然后买入，其中1≤t≤n(当t=1时，就是一开始购买)。

(i)当n较小时，总是租用。在这种情况下，投资者花费的租用金总额是租用函数g(t)=t当t=n时的函数值，即g(n)=n。

(ii)当n较大时，租用t-1次然后买入，其中1≤t≤n。在这种情况下，投资者花费的资金总额是f(t)=t-1+(1-ρ)t-1s。

下面，我们来讨论(i)(ii)两种情况中的临界值及(ii)中t的取值。

因此，此时最优离线策略是当n

因此，此时最优离线策略是当n

通过上面的分析，如果用COPT(n)表示最优离线策略的花费，我们可得到下面的定理1。

定理1对于购买价格以优惠率ρ(0<ρ<1-e-1)等比递减的在线租赁问题，有

3最优在线策略

在本节中，我们讨论购买价格以优惠率ρ(0<ρ<1-e-1)等比递减的在线租赁问题的最优在线策略。

我们给出下面的在线策略Sρ并分析其竞争比、证明最优性。

在线策略Sρ：对于购买价格以优惠率ρ(0<ρ<1-e-1)等比递减的在线租赁问题，根据ρ的大、小分以下两种情况：

定理2对于购买价格以优惠率ρ(0<ρ<1-e-1)等比递减的在线租赁问题，在线策略Sρ的竞争比

综合以上讨论可知，策略Sρ的竞争比R在区间(0,1-e-1)上是ρ的连续且严格单调减函数。

推论1证毕。

定理3对于购买价格以优惠率ρ(0<ρ<1-e-1)等比递减的在线租赁问题，在线策略Sρ是该问题唯一最优策略。

(1)对于任意使用时间实例t1,t2,…,tn，策略S′每一期都租用设备。

(2)对于任意使用时间实例t1,t2,…,tn，策略S′一开始就购买设备。

令n=1，则策略S′所花费用为s，最优离线策略所花费用为1，因此

(3)对于任意使用时间实例t1,t2,…,tn，策略S′租用设备t-1期后在t期购买设备，其中0

令n=t，由于t

(4)对于任意使用时间实例t1,t2,…,tn，策略S′租用设备t-1后在t期购买设备，其中t>s*。

令n=t，则策略S′所花费用为t-1+(1-ρ)t-1s，最优离线策略所花费用为s*=t*-1+(1-ρ)t*-1s。由于t>s*>t*时，函数f(t)=t-1+(1-ρ)t-1s为增函数，因此

定理3证毕。

4小结

经典的在线租赁研究是基于Karp提出的租雪橇模型，一般都是在假定购买价格保持恒定不变的情况下考虑问题的。考虑到现实经济活动中一些设备的购买价格是随着供求关系不断发生变化的，本文考虑了购买价格递减的在线租赁问题。虽然当购买价格呈等比递减趋势下降时，在线租赁的模型比原Karp模型复杂化，但我们针对购买价格等比递减的特征给出的最优在线策略具有更小的竞争比。从原Karp模型的竞争比2-1/s下降到R=1+[(1-ρ)s*-1s-1]/s*，而且R是ρ在区间(0,1-e-1)上的连续且严格单调减函数，并有1

参考文献：

[1]Karp R. On-line algorithms versus off-line algorithms: how much is it worth to know the future?[C]. Proc. IFIP 12th World computer congress. The Netherlands: North-Holland Publishing Co., 1992, 1: 416-429.

[2]Karlin A R, Manaees M S, McGeogh L, Owichi S. Competitive randomize algorithms for non-uniform problems[J]. Algorithmica, 1994, 11(6): 542-571.

[3]El-Yaniv R, Karp R. Nearly optimal competitive online replacement olicies[J]. Mathematics of Operations Research, 1997, 22(4): 814-839.

[4]El-Yaniv R, Kaniel R, Linial N. Competitive optimal oline leasing[J]. Algorithmica, 1999, 25: 116-140.

[5]Irani S, Ramanathan D. The problem of renting versus buying[Z]. Personal communication, 1998.

[6]Azar Y, et al. On capital investment[J]. Algorithmica, 1999, 25: 22-36.

[7]Fujiwara H, Iwama K. Average-case competitive analysis for ski-rental problems[J]. Algorithmica, 2005, 42(1): 95-107.

[8]Xu Y F, Xu W J, Li H Y. On the online rent or buy problem in probabilistic environments[J]. Journal of Global Optimization, 2007, 38(1): 1-20.

[9]王扬,徐维军,徐寅峰.一类占线融资租赁问题的最优竞争策略与风险补偿模型[J].管理学报，2011，8(12)：1866-1871.

[10]董玉成，徐寅峰，徐维军.可退货在线租赁竞争分析及其风险回报模型[J].中国管理科学，2007，15(4)：28-33.

[11]胡茂林.可分资产的在线租赁策略及其竞争分析[J].系统工程理论与实践，2011，31(1)：144-150.

[12]徐维军，张卫国，胡茂林.购买价格和租金费用均连续可变的在线竞争策略分析[J].中国管理科学，2006，14(2)：96-101.

[13]堵丁柱.k-车服务问题与竞争算法[J].数学的实践与认识，1991，(4)：36-40.

[14]马卫民，王刊良.局内管理决策问题及其竞争策略[J].管理科学学报，2003，6(2)：29-34.