基于区间数DEA的贷款定价模型研究

基于区间数DEA的贷款定价模型研究

迟国泰1，杜永强1，郝熙格2，刘峻伯3

(1.大连理工大学工商管理学院，辽宁大连116024;2.大连理工大学物理与光电工程学院，辽宁大连116024；3.大连理工大学数学科学学院，辽宁大连116024)

摘要：在贷款的买方市场或充分竞争的金融环境中，贷款利率不会由银行自己说了算，因此建立银企双方共同接受的贷款利率定价模型在现实中尤为重要。本文采用区间数的形式反映存款利息支出率、违约风险补偿率等定价指标的不确定性，以已结清贷款最小定价效率、最大定价效率组成的贷款定价效率区间为目标，以新贷款的贷款利率为决策变量，通过逆向求解区间数DEA模型反推出新贷款的贷款利率区间，建立了基于区间数DEA的贷款定价模型。本文的创新与特色一是以已结清贷款的存款利息支出率、目标利润率等指标为输入，以已结清贷款的贷款利率为输出，利用DEA模型求得已结清贷款的实际最小效率及最大效率。二是以银企双方均可接受的贷款定价效率区间为目标、以新贷款的存款利息支出率等用区间数形式表示的贷款成本为投入，反推出贷款利率的取值区间。三是通过区间数形式来反映违约风险补偿率、目标利润率等定价指标的不确定性，改变了现有研究将目标利润、贷款费用、违约损失等变量看作常数来定价的不合理现状。研究表明：存款利息支出率、费用支出率、违约风险补偿率及目标利润率均与贷款利率成正比。企业提高在贷款银行中的资金结算比率、存贷比率可以降低贷款利率。

关键词：贷款定价；区间数；可接受利率；DEA；贷款利率

收稿日期：2013-09-13

基金项目：国家自然科学基金资助项目(71171031,71472027)；国家自然科学基金青年科学

作者简介：迟国泰(1955-),男，教授，博士生导师，管理科学与工程博士；杜永强(1984-),男，博士生，；郝熙格(1992-),女，电子科学与技术专业本科生；刘峻伯(1993-)，男，应用数学专业本科生。

中图分类号：F830.33文章标识码：A

Research on Loan Pricing Model Based on the Interval DEA

CHI Guo-tai1, DU Yong-qiang1, HAO Xi-ge2, LIU Jun-bo3

(1.SchoolofBusinessManagement,DalianUniversityofTechnology,Dalian116024,China; 2.SchoolofPhysicsandOptoelectronicEngineering,DalianUniversityofTechnology,Dalian116024,China; 3.SchoolofMathematicalScience,DalianUniversityofTechnology,Dalian116024,China)

Abstract:In the buyer’s market of loan or the sufficiently competitive financial environment, the loan interest rate will not be decided by banks alone. Therefore, to establish mutually acceptable loan interest rate pricing model between the bank and enterprise is particularly important in the reality. In this paper, we use interval numbers to reflect the deposit interest rate, compensation rate of default risk and some other uncertainties of pricing indicators. We make up loan pricing efficiency interval with the old loan minimum and maximum pricing efficiency. Then we take them as the target and use the new loan interest rate as decision variables. We establish the new loan pricing model based on interval number DEA through reversely solving interval DEA model. The innovation and contributions lie in, firstly, taking the deposit interest rate of the old loan, target profit margin and some other pricing indicators as inputs and old loan interest as outputs, and using DEA model to get the actual minimum and maximum pricing efficiency of the old loan; secondly, taking mutually acceptable loan pricing efficiency interval as the outputs and take interval number pricing indicators, such as interval number deposit interest rate of new loans as inputs. In this way, we can get the loan rate interval; thirdly, using interval numbers to reflect compensation rate of default risk, target profit margin and other pricing indicators instead of constant numbers, so as to change the unreasonable situation that the current study uses constant numbers to represent these parameters. research result shows that deposit interest rate, expense rate, compensation rate of default risk and target profit margin are proportional to the loan interest rate. The loan interest rate can be reduced through improving capital settlement ratio and loan-to-deposit ratio.

Key words:loan pricing; interval number; acceptable interest; DEA; loan interest rates

0引言

贷款定价是商业银行的核心问题，资产定价问题也是现代金融学领域三大核心问题之一。

银行为企业贷款定价时，每笔贷款的成本往往具有不确定性，并非是一个确定的常数。由于不确定的成本会产生不确定的收益，不确定的贷款成本给银行带来的收益不应该是一个确定的常数。同时，在贷款的买房市场或充分竞争的金融环境中，贷款利率不会由银行自己说了算。银行往往不顾忌客户的接受能力、一味追求利润最大化也导致了客户的流失[1]。因此，如何在不确定成本及收益的背景下建立银企双方均可接受的贷款定价模型是亟待解决的问题。

现有贷款定价研究可分为以下五类。

一是基于关系型的贷款定价模型。代表性的研究有：Hannagan研究了银行与客户的关系对贷款定价的影响[1]。何韧[2]实证分析了银企关系与银行贷款定价的联系，发现企业与较多银行建立关系有助于贷款价格成本的降低，但企业与银行建立关系的时间长短却不是贷款价格降低的原因所在。邓超等分析了大银行和小企业的共生关系，建立了合理分配关系租金收益、实现利润跨期补偿的关系型贷款定价模型[3]。

二是基于价格领导的贷款定价模型。代表性的研究有：Edelberg研究了违约风险对贷款价格的影响，得出了基准利率应该提高等三个结论[4]。毛捷根据我国金融机构贷款定价决策的经验事实，建立了一个基于亚式期权定价方法的内生违约贷款定价模型[5]。

三是基于成本加成的贷款定价模型。代表性的研究有：Stango将客户转换成本引入到成本加成定价法中，研究了违约风险和转换成本之间的关系，进而为贷款定价[6]。Stein采用改进的定点法来确定信用等级，构建了基于成本加成的贷款定价模型[7]。

四是基于结构化方法的贷款定价模型。代表性的研究有：Lee利用遗传算法反推出KMV模型中的最佳违约点，并利用改进的KMV模型，测算了企业的违约概率[8]。迟国泰等根据理论违约率与实际违约率的总体差异最小的思路，建立规划模型，确定了KMV模型的最优长期负债系数，建立未发债上市银行的违约概率并应用于实际计算违约概率[9]。由于此模型只考虑了上市企业而忽略了未上市企业，有其局限性，应用范围大打折扣。

五是基于最优效率的贷款定价模型。代表性的研究有：隋聪利用二分法求解DEA模型，实现了贷款定价效率的最大化定价[10]。隋聪提出了效率定价的SFA模型，通过随机生产函数中过去的技术非效率项,推导未来可达到最大SFA效率来反映客户未来对贷款利率的接受程度[11]。迟国泰以Malmquist指数为工具，通过过去银行的DEA效率推导未来时段可达到最大DEA效率，并用未来效率确定贷款定价，进一步完善了基于DEA效率的贷款定价模型[12]。

现有贷款定价方法的局限性在于：一是忽略贷款价格能否同时被银企双方接受。二是未考虑贷款成本、收益存在着不确定性。事实上，由于每笔贷款的成本存在着不确定性，贷款的价格也不应该是一个确定的常数。

综上所述，本研究建立基于区间数DEA的贷款定价模型，得到了银企双方均可接受的贷款利率区间。

1基于区间数DEA的贷款定价原理

1.1问题性质

在不确定成本及收益的背景下确定银企双方均可接受的贷款利率区间的作用有三：一是为决策者提供了富有弹性的决策空间；二是为银行的贷款业务拓展了市场竞争力；三是有助于稳定银行的客户资源。

1.2问题的难点

难点1如何确定银企双方均可接受的贷款定价效率区间。合理的贷款定价效率区间既要保证在覆盖贷款成本和风险的情况下给银行带来收益，又要保证贷款利率能够被客户所接受。

难点2如何在银行贷款成本和收益不确定的背景下，给出银企双方均能接受的贷款利率区间。不确定的成本产生不确定的收益，给出银企双方均能接受的贷款利率区间，可以为商业银行决策者在为贷款定价时提供决策空间。

1.3突破难点的思路

(1)通过求解已结清贷款的DEA效率，确定银企双方均可接受的贷款定价效率区间。通过以已结清贷款的违约风险补偿率、目标利润率等4个反映贷款成本的指标作为投入变量，以已结清贷款的贷款利率作为产出变量，计算每笔已结清贷款的DEA效率θi，已结清贷款的最小效率值θmin及最大效率值θmax组成的效率区间[θmin，θmax]就是银企双方均可接受的贷款定价效率区间。解决难点1。

(2)通过区间数DEA贷款定价模型，反推出贷款利率区间，确定银行与客户均能接受的贷款利率区间。以区间数形式表示每笔新贷款的存款利息支出率、违约风险补偿率等定价指标为投入，以银企双方均可接受的贷款定价效率区间[θmin，θmax]为目标，以新贷款的贷款利率区间为产出，通过逆向求解区间数DEA模型，反推出新贷款的利率区间，建立基于区间数DEA的贷款定价模型，解决难点2。

1.4投入、产出指标体系的建立

1.4.1投入指标

以国内外有关贷款定价的典型文献[1～12]为依据，考虑定价能否覆盖贷款的财务成本、补偿违约风险、实现目标利润等因素，选取存款利息支出率、目标利润率、违约风险补偿率、费用支出率等4个指标作为定价模型的输入。

(1)存款利息支出率指企业为得到贷款本金所需要支付的存款利息。

(2)目标利润率反映了贷款为商业银行股东提供的资本收益水平。

(3)违约风险补偿率指由于贷款企业具有违约的可能性，而产生的贷款利率高于无风险利率的那部分，用于补偿企业贷款的预期违约损失。

(4)费用支出率指除了存款利息支出以外的，包括营业费用、固定资产折旧费和其他营业支出。

其中，通过存款利息支出率、费用支出率等2个指标反映贷款利率对贷款财务成本的覆盖程度；通过违约风险补偿率反映了贷款利率对违约风险的补偿程度；通过目标利润率反映了贷款为商业银行股东提供的资本收益水平，即贷款的目标利润水平。

1.4.2产出指标

以贷款利率作为区间数DEA贷款定价模型的产出指标。在本文中，已结清贷款的贷款利率是已知量，新发放贷款的贷款利率区间是待求变量，本文的目的就是要确定新发放贷款的贷款利率区间。贷款定价的投入、产出指标，如表1所示。基于区间数DEA的贷款定价模型原理详见图1。

表1　投入、产出指标

图1基于区间数DEA的贷款定价模型原理

2基于区间数DEA的贷款定价模型

2.1银企双方可接受的定价效率区间的确定方法

设：θ—贷款效率，是决策变量；n—贷款数；μj—第j笔贷款投入、产出指标的系数，是决策变量；xij—第j笔贷款的第i个定价指标；xi0—待评价贷款的第i个定价指标；yj—第j笔贷款的贷款利率；y0—待评价贷款的贷款利率，则DEA模型如下[13]：

minθ

(1)

(2)

(3)

μj≥0,(j=1,2,…,n)

(4)

若DEA的效率θ小于1，表示贷款没有达到最优效率；若DEA的效率θ等于1，表示贷款是效率最优的[13]。

通过以每笔已结清贷款的存款利息支出率、违约风险补偿率等指标为输入，以已结清贷款的贷款利率为输出，利用DEA模型(式(1)～(4))，计算每笔已结清贷款的效率值θi。

银行已发放且顺利收回本金和利息的贷款，说明其定价利率及贷款效率是被银企双方所能接受的。则银行发放的、且被顺利收回本金和利息的最小定价效率θmin和最大定价效率θmax组成的效率区间[θmin，θmax]就是银企双方均可接受的贷款定价效率区间。

2.2贷款利率区间的确定方法

在银行贷款成本和收益不确定的情况下，给出银企双方均能接受的贷款利率区间。不确定的成本产生不确定的收益，富有弹性的贷款价格更可以为决策者和客户所接受。

以区间数的形式表示每笔新贷款的投入指标，反映了贷款成本的不确定性；以区间数的形式表示每笔新贷款的利率，反映了银行收益的不确定性。

(5)

(6)

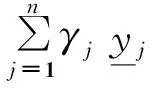
(7)

γj≥0,(j=1,2,…,n)

(8)

(9)

(10)

(11)

γj′≥0,(j=1,2,…,n)

(12)

本模型与贷款定价现有研究[1～12]区别有二：一是现有贷款定价研究[4～12]侧重于财务成本和风险补偿的测度，忽略了银企关系对贷款利率的影响，导致定价过高、客户无法接受。本模型利用已结清贷款数据得到的实际定价效率，确定了银企双方均可接受的定价效率区间，并以这个定价效率区间为目标，以新贷款的存款利息支出率、费用支出率等用区间数形式表示的贷款成本为投入，反推出银企双方均可接受的贷款利率区间。确定出银企双方均可接受的贷款利率区间正是本文基于区间数DEA贷款定价方法的第一个优势。

二是现有贷款定价研究[1～12]将目标利润、贷款费用等贷款成本变量当做常数来为贷款定价。忽略了贷款成本往往具有不确定性的事实，导致得到的贷款利率缺乏弹性。本模型通过区间数形式来反映目标利润率、费用支出率等定价成本的不确定性，最终得到以区间数形式表示的贷款利率区间，为银行提供富有弹性的决策空间。这正是本文基于区间数DEA贷款定价方法的第二个优势。

事实上，如果将贷款的成本变量(例如：存款利息支出率、目标利润率)看作贷款的投入变量，将贷款利率看作贷款的产出变量，则贷款定价问题就可以被看作区间数DEA方法中的“投入→产出→效率”问题，而本文正是基于区间数DEA方法中的“投入→产出→效率”分析了企业的贷款定价问题。考虑了贷款的价格能否被银企双方所接受、贷款成本及收益的不确定性这两个方面正是本文与现有研究的区别所在。

按照式(8)～(12)的区间数DEA贷款定价模型进行定价，能够得到不确定贷款成本、收益背景下银企双方均可接受的贷款利率区间，使银行在为新贷款进行定价时富有决策空间。

2.3区间数DEA贷款定价模型的求解思路

图2　基于区间数DEA贷款定价模型的求解技术路线

基于区间数DEA贷款定价模型的求解技术路线，详见图2。

3应用实例

3.1实例数据

假设某银行有20笔到期后均已收回本金和利息的已结清贷款。这20笔贷款的存款利息支出率、费用支出率、违约风险补偿率、目标利润率及贷款利率等5个指标的数据如表2第1到5列所示。

某银行有5笔待发放的新贷款，新贷款的存款利息支出率、费用支出率、违约风险补偿率、目标利润率等4个指标的数据如表3第1到4列所示。

3.2银企双方可接受的定价效率区间的确定

将表2第1～5列数据代入式(1)～(4)，利用MAXDEA软件，得到已结清贷款的贷款效率θ，列于表2第6列。

表2第6列贷款效率θ的最小值是0.8119，最大值是1.0000。由这个贷款效率θ的最小值、最大值组成的定价效率区间[0.811 9,1.0000]就是银行和客户双方均可接受的贷款定价效率区间。

3.3待发放贷款利率区间的确定

银行贷款实践中，贷款利率不会超过20%，因此待发放的贷款利率取值区间为[0，20%]。

同理，求得其他4笔待发放贷款的贷款利率区间，列入表3第5列的相应行。

3.4结果分析

存款利息支出率、费用支出率、违约风险补偿率及目标利润率均与贷款利率成正比。

由表3第1、2行可知，不考虑其它指标因素对贷款利率影响的情况下，存款利息支出率越高、其所对应的贷款利率也越高。

由表3第1、3行可知，不考虑其它指标因素对贷款利率影响的情况下，费用支出率越高、其所对应的贷款利率也越高。

由表3第1、4行可知，不考虑其它指标因素对贷款利率影响的情况下，违约风险补偿率越高、其所对应的贷款利率也越高。

由表3第1、5行可知，不考虑其它指标因素对贷款利率影响的情况下，目标利润率越高、其所对应的贷款利率也越高。

3.5确定最终贷款利率的建议

通过区间数DEA贷款定价模型得到的贷款利率是一个区间数，为使银行和贷款企业间达成最终的贷款利率，下面给出确定最终贷款利率的2条建议：

(1)企业提高在贷款银行中的资金结算比率、存贷比率可以降低贷款利率。

资金结算比率指企业在贷款银行的结算量占企业全部结算量的比值。企业在贷款银行的结算量越大，其给银行带来的收益就越高，在贷款利率区间范围内银行可以适当降低贷款利率。因此，企业如果想获得较低的贷款利率，可以提高在贷款银行中的业务结算量。

存贷比率指企业在贷款银行的存款占贷款的比率。企业在贷款银行的存款量越大，其给银行带来的收益就越高，在贷款利率区间范围内银行可以适当降低贷款利率。因此，企业如果想获得较低的贷款利率，可以整合在贷款银行中的存款资源，提高在贷款银行中的存款量。

事实上，企业在贷款银行中的资金结算比率及存贷比率，均体现了企业与银行之间的关系。良好的银企关系是降低贷款利率的必要条件[2]。

(2)参照贷款时刻的宏观经济状况确定最终的贷款利率。

当宏观经济状况不景气时，在贷款利率区间范围内银行可以通过降低贷款利率、扩大发放贷款数量来达到促进经济发展的目的；当宏观经济状况处于繁荣时期，在贷款利率区间范围内银行可以通过适当提高贷款利率，抑制经济过热发展。

表2　已结清贷款的数据

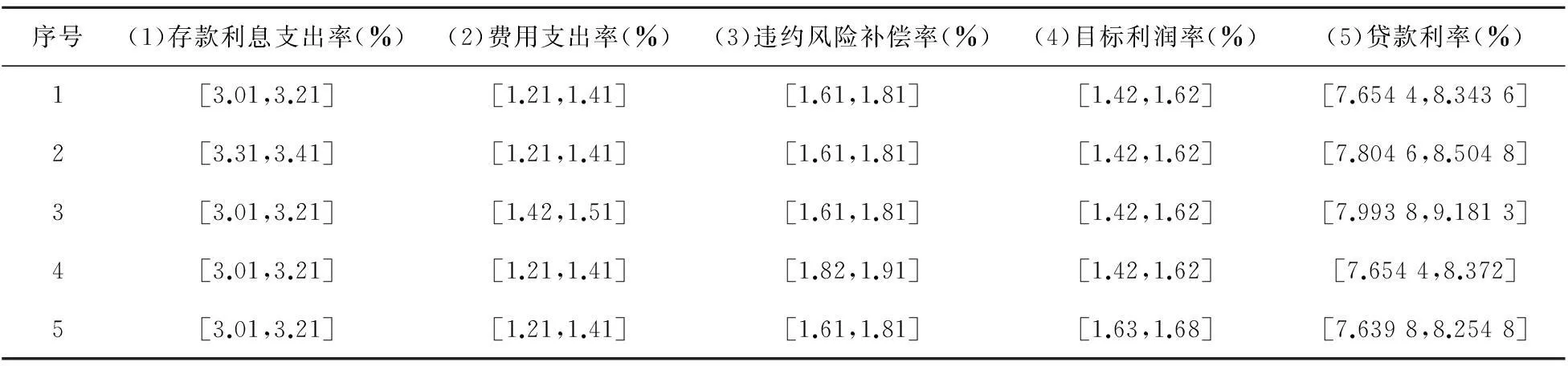
表3　新发放贷款的数据

4主要结论与特色

4.1主要结论

(1)在贷款的买方市场或充分竞争的金融环境中，贷款利率不会由银行自己说了算。建立银企双方均能接受的贷款定价模型在现实中尤为重要。

(2)不确定的贷款成本，会产生不确定的贷款收益。银行在为贷款定价时，既要兼顾贷款成本与贷款利率的不确定性，同时也要兼顾银行的利益。

(3)研究表明：存款利息支出率、费用支出率、违约风险补偿率及目标利润率均与贷款利率成正比。

4.2主要特色

(1)以已结清贷款的存款利息支出率、目标利润率等指标为输入，以已结清贷款的贷款利率为输出，利用DEA模型求得已结清贷款的实际最小效率θmin及最大效率θmax。

(2)以银企双方均可接受的贷款定价效率区间[θmin，θmax]为目标、以新贷款的存款利息支出率、费用支出率等用区间数形式表示的贷款成本为投入，反推出贷款利率的取值区间。改变了现有研究侧重于财务成本和风险补偿的测度，忽略了银企关系对贷款利率的影响，导致定价过高、客户无法接受。

(3)通过区间数形式来反映违约风险补偿率、目标利润率、费用支出率等定价指标的不确定性，改变了现有研究将贷款成本、违约损失等变量看作常数，得到的贷款利率也为常数、缺乏弹性的弊端。

参考文献：

[1]Hannagan T A. Loan and relationship pricing practice[J].The RMA Journal , 2004, 87(4): 60-62.

[2]何韧.银企关系与银行贷款定价的实证研究[J].财经论丛,2010,(1):57-63.

[3]邓超,敖宏,胡威,王翔.基于关系型贷款的大银行对小企业的贷款定价研究[J].经济研究,2010,(2):83-96.

[4]Edelberg W. Risk-based pricing of interest rates for consumer loans[J]. Journal of Monetary Economics, 2006, (53): 2283-2298.

[5]毛捷,张学勇.基于亚式期权模型的贷款定价研究—来自中国的经验事实与理论模型[J].金融研究,2009,(5):71-83.

[6]Stango V. Pricing with consumer switching costs: evidence from the credit card market[J]. The Journal of Industrial Economics, 2002, 55(4): 475-491.

[7]Stein R M. The relationship between default prediction and lending profits: integrating ROC analysis and loan pricing[J]. Journal of Banking & Finance, 2005, 29(5): 1213-1236.

[8]Lee W C. Redefinition of the KMV model’s optimal default point based on genetic algorithms-evidence from taiwan[J]. Expert Systems with Applications, 2011, 38: 10107-10113.

[9]迟国泰,曹勇,党均章.基于最优负债系数的上市银行违约概率测算模型与实证[J].运筹与管理,2012,21(3):176-186.

[10]隋聪,迟国泰,闫达文.基于DEA二分法的贷款定价模型[J].预测,2009,28(5):27-31.

[11]隋聪,迟国泰.基于随机生产函数的贷款定价模型及应用[J].管理科学学报,2010,13(9):16-25.

[12]迟国泰,隋聪.基于未来DEA效率的贷款定价模型[J].系统工程理论与实践,2011,31(1):18-27.

[13]Wei Q L, Zhang J Z, Zhang X S. An inverse DEA model fou inputs/outputs estimate[J]. European Journal of Operational Research, 2000, (121): 151-163.

[14]吴文江.指标可取区间数的决策单元的DEA评价[J].数学的实践与认识,2009,39(2):1-9.