基于可拓学理论的高维大数据相似性研究

2016-01-18袁瑞萍,师鸣若

运筹与管理 2015年5期

基于可拓学理论的高维大数据相似性研究

袁瑞萍，师鸣若

(北京物资学院信息学院，北京101149)

摘要：高维大数据的相似性计算是数据挖掘领域的研究重点，论文通过分析高维大数据相似性计算的难点，提出采用可拓学的方法解决其中矛盾问题的研究思路。在基元表示高维大数据的基础上，借助数据转换、数据筛选、权重的确定、数据预处理等技术实现了数据之间的相似性计算，并基于水污染常规分析数据进行了算法验证。论文借助可拓的思想研究大数据相似性的问题，不仅对数据挖掘的研究有一定的理论促进，同时也为可拓学的研究提供了新的应用空间。

关键词：大数据；高维数据；可拓学；相似性

收稿日期：2015-06-04

基金项目：北京市教委科技计划面上项目(KM201510037001)；智能物流系统北京市重点实验室(NO:BZ0211)；北京市属高等学校创新团队建设提升计划项目(项目号:IDHT20130517)

作者简介：袁瑞萍(1982-)，女，博士，讲师,山东荷泽人,研究方向:物流信息化,数据挖掘;师鸣若(1976-),女,河南郑州人,研究方向:商务智能。

中图分类号：TP311.1文章标识码：A

Research on the Similarity of High Dimensional Big Data Based on Extenics

YUAN Rui-ping, SHI Ming-ruo

(SchoolofInformation,Beijingwuziuniversity,Beijing101149，China)

Abstract:The similarity calculation of high dimensional big data is a research focus in the field of data mining. In this paper, after analyzing the difficulty of similarity calculation of high dimensional data, a method based on extenics is put forward to solve the contradictory problems. Firstly, the element is used to represent high dimensional data. Then the similarity between data is calculated by means of data conversion, data selection, weight determination and data pre-processing technology. Finally the conventional analysis data of water pollution is used to verify the method. The idea of using extenics to solve similarity problem of big data can not only promote theoretical research of data mining, but also provide a new application for extenics.

Key words:big data; high dimensional data; extenics; similarity determination

0引言

2008 年9月，《科学》杂志发表文章《Big Data: Science in the Petabyte Era》,“大数据”一词正式走入公众视线，并开始传播。其实，“大数据”一词早在上个世纪80年代由美国人提出来[1,2]。2011年6月，IDC研究报告《从混沌中提取价值》中三个基本论断构成了大数据的理论基础，人们对大数据的关注程度日益上升。据统计，Google“大数据”搜索量自2011年6月起呈直线上升趋势，大数据时代的到来毋庸置疑[3]。根据国际数据资讯(IDC)公司监测，全球数据量大约每两年翻一番，预计到 2020 年，全球将拥有 35ZB 的数据量，并且 85%以上的数据以非结构化或半结构化的形式存在。“大数据”2011年一路走红，2012年后更加闪耀，成为业界当之无愧的焦点，很多国内外的学术会议均以“大数据”冠名。伴随新型SNS 网络的发展、视频流量的猛增及图片分享需求的涌现，人们迷失于茫茫的数据海洋中，如何从大数据中挖掘出有用的信息成为关注的焦点，其中高维大数据因其复杂性而备受关注，并成为数据领域中的研究热点和前沿问题。

1高维大数据相似性研究综述

聚类分析是高维数据处理的主要内容，它根据数据对象属性信息或对象间关系，将数据对象分成类或簇，使得同一个簇中对象之间具有较高相似度，而不同簇中对象彼此差别较大，即通常所说的“类内聚合度高，类间耦合度低”。传统的聚类算法包括分层法、划分法、基于密度的方法和基于网格的方法等[3]。各种聚类算法的基础都是数据相似性计算，因此探讨数据的相似性是聚类实现的根本。但是，高维数据的相似性计算存在一定的困难，这种困难不仅体现在聚类算法效率的下降，更重要的是由于高维空间的稀疏性和最近邻特性使得在高维空间中几乎不可能存在数据簇，还有就是高维数据中的非结构化数据让问题变得难以表述。

高维数据的相似性一般用距离函数(或相似度函数)表示，距离不单是空间上的距离，也包括时间、状态、语义、密度等产生的差距。常见的距离有欧几里得距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离、相关系数和夹角余弦距离等等。目前为止，还没有一个能适用于所有聚类任务的距离函数，在不同的聚类问题中应该设计不同的相似性度量。Apostolico等[4]提出一种快速计算生物序列距离的方法；Vinga 等[5]比较了几种用于计算 SCOP蛋白质数据集的序列距离计算方法；Ververidis 等[6]考虑了马氏距离在高维空间中的信息丢失问题；Yu 等[7]提出一种估计样本间相似度的通用向导。

王晓阳等[8]针对传统数据相似性度量算法在高维数据空间的不适应性，通过分析传统距离度量方法，结合高维数据特性，提出了新的高维数据相似性度量函数，该方法在处理高值数据之间与低值数据之间的相对差异方面更具优势。邵昌昇等[9]对传统度量算法进行改进，提出新的Close函数，以弥补传统相似性度量算法应用在高维空间时的不足。谢明霞等[10]提出了高维数据相似性度量函数的改进HDsim(X,Y)函数，该函数整合了各类型数据的相似性度量方法，在处理数值型、二值型以及分类属性数据上充分体现了原Hsim(X,Y)函数处理数值型数据、Jaccard系数处理二值数据以及匹配率处理分类属性数据的优越性。黄斯达等[11]针对传统基于距离度量的聚类算法难以适合高维数据聚类以及高维数据之间相似度难定义的问题，首先计算对象两两之间的相似度并得出相似度矩阵，然后根据该相似度矩阵和阈值大小自底向上对数据进行聚类分析。

以上研究分析表明，在高维数据处理的研究领域，尤其是基于相似性度量的聚类分析中，学者们致力于算法的改进和优化，应用于不同数据处理会得到不同的结果，但是到底哪种算法更适合处理高维数据尚无定论。因此，走出原有的研究路径，寻找新的突破口是实现算法优化的一个思路。

2可拓学的引入

可拓学[12]是用来解决矛盾问题的一种方法，采用形式化的模型，实现了定性与定量的结合。高维数据处理中大量非结构化数据的客观存在，为可拓学的应用奠定了基础。

作为哲学、数学与工程学交叉的一门新兴学科[13,14]，可拓学在各门学科和工程技术领域中应用的成效, 不在于发现新的实验事实, 而在于提供一种新的思想和方法。为了解决具体的矛盾问题，可拓学研究者探讨了能处理一般矛盾问题和领域中矛盾问题所需要的形式化模型、定量化工具、推理的规则和特有的方法, 在理论、方法和技术上都取得了一定的进展[15]。高维数据处理中，数据属性的分析、数据归类、数据相似性计算、数据阈值确定等都属于矛盾性的问题，这些矛盾的处理可以借助于可拓学的思路来解决。

可拓创新方法是可拓学中特有的方法，通过对研究对象的拓展、变换、评价等，以生成解决各种矛盾问题的创意的形式化、定量化方法。可拓创新方法的基础是基元[16]，基元包括物元、事元和关系元[17]。其中，物元是应用最为广泛也是最早提出的基元，其一般定义为：以物Om为对象，cm为特征，Om关于cm的量值vm构成的有序三元组M=(Om,cm,vm)作为描述物的基本元，称为一维物元，Om,cm,vm三者称为物元的三要素，其中cm,和vm构成的二元组(cm,vm)称为物Qm的特征元。这里，量值vm可以是数量化量值，也可以是非数量化量值。大数据时代，海量的半结构化和非结构化数据的处理正好契合了特征元的思想。量值vm在事物的定性描述和事物的定量评价之间架起了一座桥梁。在高维数据处理方面，二元组(cm,vm)将高维数据中的结构化数据和非结构化数据有机结合起来。所以，借助可拓学的思想和方法来解决高维数据处理问题成为可能。

3基于可拓学理论的高维大数据相似度计算过程

可拓学方法因其独有的形象化表示方法，在对定性和定量问题的研究中具有一定的优势，尤其在定性研究方面更具特色。采用该方法进行高维数据相似性计算基于以下几个环节。

(1)采用基元表示系统中的研究对象，其中涵盖定性数据和定量数据。

如何定义相似性计算公式是问题的重点，但对高维数据来说，用形式化的语言描述高维数据是问题的起点。基元是可拓学的逻辑细胞[18,19]，也是采用可拓学研究问题的基础。

借助基元中物元的形式化表示符号M=(Qm，cm,vm)将高维数据的某一条记录描述为多维物元形式，即：

(1)

其中，Mi(i=1,2,…,n)代表高维数据物元；

Qi(i=1,2,…,n)代表某一条数据记录，并设定数据总量为n，在大数据背景下，n值将很大；

cj(j=1,2,…,m)代表高维数据属性，该属性可以是结构化的也可以是非结构化的，并设定数据维度为m；

vji(j=1,2,…,m;i=1,2,…,n)代表高维数据系统中属性cj的取值，这个取值可以是定量的数据，也可以是定性数据，可以是结构化数据，也可以是非结构化数据。

需要说明的是，高维大数据中稀疏性[18]的客观存在，高维数据物元中很多量值V均为空，此时可以用0补齐。

(2)数据转换。将系统中的定性数据转化为定量数据，一般的将“是”和“否”二维逻辑数据转化为1和0，其他定性数据可以视具体情况而定。

(3)数据筛选。一方面，在多维数据中，有些数据是冗余数据，这些数据会带来计算复杂度的提升，因此剔除可见的冗余数据对于计算是有益的；另一方面，基于数据的应用目标，有些数据在相似性研究或者问题的解决中不起任何作用，可以剔除。

(4)权重的确定。采用函数Hsim(X,Y)计算两个对象之间的相似性需要定义属性的权重。常用的权重确定方法有相对比较法、专家打分法和层次分析法等，也可以采用可拓权重法，基于各个待评对象关于各评价指标的取值，借助关联函数获得。

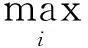
(6)数据补齐。数据稀疏性是多维大数据的基本属性，一般的可以根据属性间关系借助粗糙集的方法补足数据，或者采用简单的设定方法获取缺失数据。

(7)计算高维数据的相似度，进而获得聚类结果。基于已有的文献可以定义两个高维数据的相似性为：

(2)

4案例应用

论文采用文献[20]中的数据进行计算。该文献探讨的是水污染常规数据聚类分析，通常水污染常规分析指标包括臭味、水温、浑浊度、pH值、电导率、溶解性固体、悬浮性固体、总氮、总有机碳(TOC)、溶解氧(DO)、生化需氧量(BOD)、化学需氧量(COD)、细菌总数、大肠菌群等，可以看成是一个高维的数据集。论文监测了海河流域上马颊河的11个监测点(采样点)的溶解氧、化学需氧量、氨氮、挥发酚和石油类等5项水质污染指标数据，为了描述问题的一般性，引入定性指标“臭味”，抽取各个指标的最优值和最劣值，获取数据如表1所示。

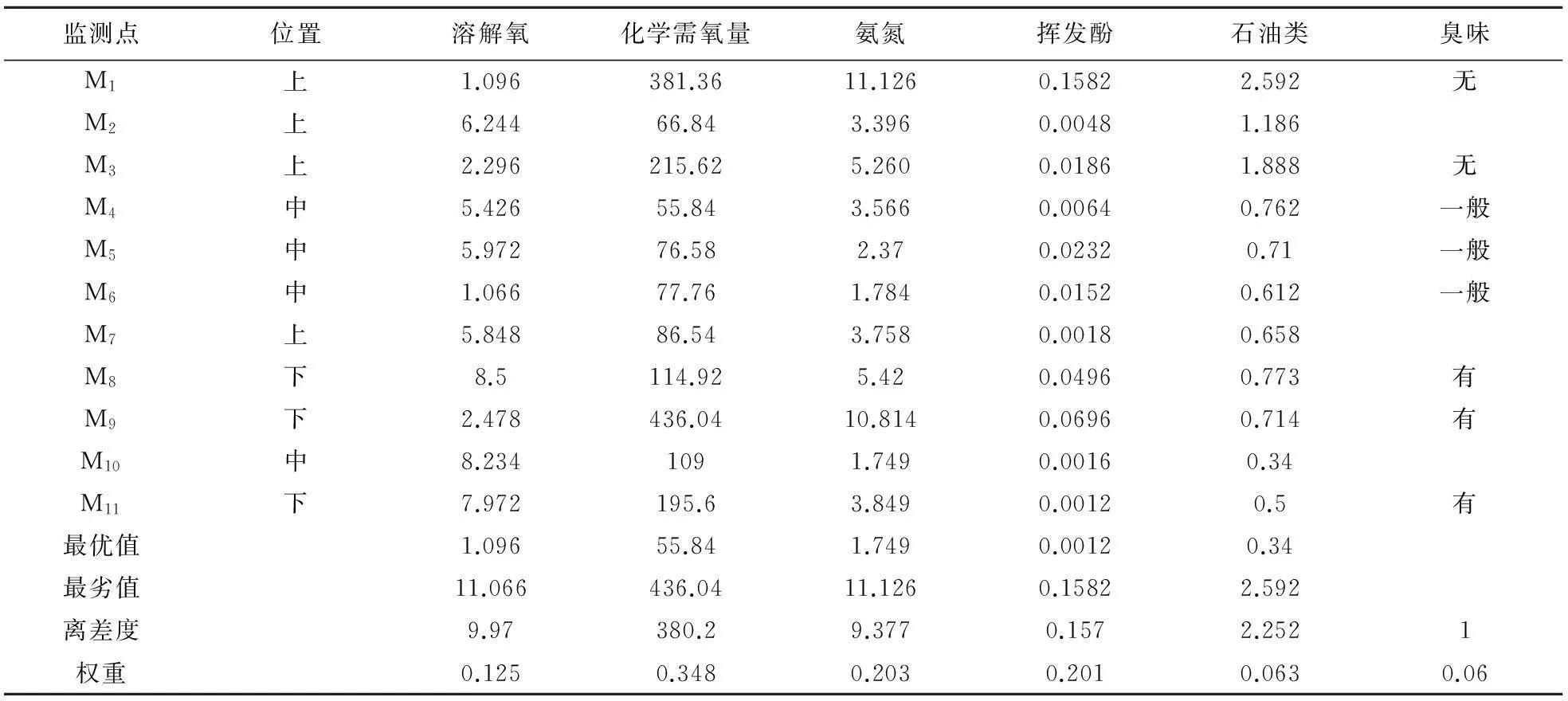
表1　监测点数据　单位：mg/L -1

(1)借助物元方法表示各个监测点，如图1所示，属性C1到C6分别表示溶解氧、化学需氧量、氨氮、挥发酚、石油类和臭味。

图1各个检测点的物元表示

(2)该数据集中属性C6的取值范围为定性数据，分别定义0,0.5,1，对应“无”、“一般”、“有”三项取值。

(3)在数据指标中，监测点的位置属于冗余数据，不需要考虑，可以剔除。

(4)获取各个指标的权重，如表1最后一行所示。

(5)根据各个指标的最优值和最劣值获取离差度，如表1倒数第二行所示。

(6)由于案例中M2，M7，M10的部分数据缺失，可以补齐，不难发现属性C6的取值与监测点的位置具有一定的对应关系，因此可以定义v6,2=0,v6,7=0,v6,10=0.5。

(7)借助相似度计算公式得到两两物元之间的相似度如表2所示。

表2　相似度计算结果

5结论

高维大数据的相似性计算是数据挖掘领域的研究重点，本文在分析高维大数据相似性计算难点基础上，提出采用可拓的方法解决其中的矛盾问题。在基元表示高维大数据的基础上，借助数据转换、数据筛选、权重的确定、数据预处理等技术实现了数据之间的相似性计算，并基于水污染常规分析数据进行了算法验证。该方法在高维数据的表示方面具有一定的优势，尤其是在定性数据表示方面。其次，该方法借助于合理的相似度计算公式可以得到数据之间的相似性度量，进而为数据的聚类分析奠定了基础。论文提出的方法对高维数据的处理具有一定的理论价值，同时也为可拓学的研究拓展了应用空间。

参考文献：

[1]冯芷艳,郭迅华,曾大军,陈煜波,陈国青.大数据背景下商务管理研究若干前沿课题[J].管理科学学报,2013,16(1):1-9.

[2]徐子沛.大数据[M].广西:广西师范出版社,2012.

[3]杨风召.高维数据挖掘中若干关键问题的研究[D].上海:复旦大学,2003.

[4]Apostolico A, Denas O. Fast algorithms for computing sequence distances by exhaustive substring composition[J]. Algorithms for Molecular Biology, 2008, 3(1): 13-16.

[5]Vinga S, Gouveia-Oliveira R, Almeida J S. Comparative evaluation of word composition distances for the recognition of SCOP relationships[J]. Bioinformatics. 2004, 20(2): 206-215.

[6]Ververidis D, Kotropoulos C. Information loss of the mahalanobis distance in high dimensions: application to feature selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2009, 31(12): 2275-2281.

[7]Yu J, Amores J, Sebe N. Distance learning for similarity estimation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2008, 30(12): 451-462.

[8]王晓阳,张洪渊,沈良忠,池万乐.基于相似性度量的高维数据聚类算法研究[J].计算机技术与发展,2013,(5):30-33.

[9]邵昌昇,楼巍,严利民.高维数据中的相似性度量算法的改进[J].计算机技术与发展,2011,(2):1-4.

[10]谢明霞,郭建忠,张海波,陈科.高维数据相似性度量方法研究[J].计算机工程与科学,2010,(5):92-96.

[11]黄斯达,陈启买.一种基于相似性度量的高维数据聚类算法的研究[J].计算机应用与软件,2009,(9):102-105.

[12]蔡文.可拓集合和不相容问题[J].科学探索学报,1983,(1):83-97.

[13]Cai Wen. Extension theory and its application[J]. Chinese science bulletin, 1999, 44(17): 1538-1548.

[14] Cai Wen, Yang Chunyan, Wang Guanghua. A new gross discipline-extenics[J]. Science foundation in china. 2005, 13(1): 55-61.

[15]杨春燕.可拓学的重要科学问题及其关键点[J].哈尔滨工业大学学报,2006,38(7):1087-1090.

[16]杨春燕.多评价特征基元可拓集研究[J].数学的实践与认识,2005,35(9):203-208.

[17]杨春燕.我国管理可拓工程研究进展[J].中国科学基金,2010,24(1):13-16.

[18]李兴森,张浩澜,陈艳.大数据及其应用的矛盾问题与可拓学[J].科技促进发展,2014,(1):45-51.

[19]崔春生.推荐系统中显式评分输入的用户聚类方法研究[J].计算机应用研究,2011,28(8):2856-2868.