基于活动延期风险加权时差的资源受限项目调度鲁棒性度量

基于活动延期风险加权时差的资源受限项目调度鲁棒性度量

何立华，孔云霄

(中国石油大学(华东)经济管理学院，山东青岛266580)

摘要：在项目调度鲁棒性研究中，当活动出现延期风险时，由于各活动性质不同，其延期风险权重也不同，权重越大的活动越有可能影响项目的完工时间。针对资源受限项目调度问题，提出一个基于活动延期风险加权时差的鲁棒性度量新指标。在出现不确定因素干扰时，该指标不仅考虑了活动延期风险权重的影响，同时为实现时差在多个任务之间的共享，还考虑了紧前任务数量的影响。建立一个以加权时差最大化为目标的资源受限项目调度鲁棒优化模型，并针对模型特点，设计了基于禁忌搜索的模拟退火算法。最后，通过算例验证了该度量方式和算法的合理性和有效性，对比分析结果表明所提出的指标优于现有的度量指标，较好地满足了项目调度质量鲁棒性的要求。

关键词：项目调度；鲁棒性；延期风险权重；时差；模拟退火

收稿日期：2014-04-04

基金项目：中央高校基本科研业务费专项资金(15CX05007B,15CX04102B,15CX08012A,14CX06037B);国家自然科学基金资助项目(71501188);山东省自然科学基金资助项目(ZR2015GM009)

作者简介：何立华(1971-)，男，安徽怀宁人，博士，副教授，研究方向：管理科学理论与应用、工程项目管理；孔云霄(1989-)，女，山东济宁人，硕士研究生，研究方向：工程管理与项目管理。

中图分类号：F224.3;C935 文章标识码：A

Robustness Measure for the Resource-constrained Project Scheduling

Problem based on Activity Delay Risk Weighted Slack

HE Li-hua, KONG Yun-xiao

(SchoolofEconomicsandManagement,ChinaUniversityofPetroleum(EastChina),Qingdao266580,China)

Abstract:During the research on the robustness of project scheduling, each activity of the project has different weight of delay risk because of its different nature when it appears delay risk. The higher the weight is, the more likely the activity will affect the makespan of the project. In view of the resource-constrained project scheduling problem, a new robustness measure index based on activity delay risk weighted slack is put forward. When uncertain factors appear, this index not only considers influences of the weight of delay risk, but also takes the number of preceding activities into account to realize the share of slack among multiple activities. A robust optimization model for the resource-constrained project scheduling problem aimed at weighted slack maximization is developed. According to the feature of the model, a simulated annealing algorithm based on the tabu search is presented. Finally, the results of the numerical example validate the reasonableness and the effectiveness of the measurement and the algorithm. Also, the superiority of the newly proposed index over the old ones is proven by comparison results and it can meet the demands of quality robustness of the project scheduling better.

Key words:project scheduling; robustness; weight of delay risk; slack; simulated annealing

0引言

伴随着日益复杂的项目建设环境，项目在实际运行过程中存在的各种天气、场地、材料、资源和机械等不确定因素急剧增加，这使得调度计划难以按时完成，提高项目调度的抗干扰能力就成为了项目调度中的关键问题，而鲁棒性是衡量项目调度稳定性的重要指标，所以对于资源受限项目调度问题(resource-constrained project scheduling problem, RCPSP)的鲁棒性研究逐渐成为研究的热点。调度的鲁棒性是指如果一些活动比计划时间延迟了一些，对于鲁棒性的项目调度，应该能够抵抗这些由于不可控因素导致的活动时间的小的增加，项目的完成时间具有较好的稳定性，并且不必消耗任何成本[1]。

文献[2～4]认为一个理想的调度方案应同时具有解的鲁棒性和质量的鲁棒性，质量鲁棒性(Quality Robustness)是指项目计划完工时间的稳定性；解鲁棒性(Solution Robustness)是指活动开始时间的稳定性。对于资源约束项目调度的鲁棒性研究，涉及控制理论应用、系统工程思想、运筹学优化建模方法及智能优化算法，是新兴的多学科交叉领域，采用什么样的度量方式对项目调度的鲁棒性进行度量是其中较为关键的核心环节[5]。

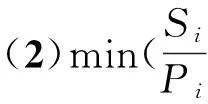
本文第一部分在描述了项目调度质量鲁棒性和解鲁棒性的两种情况之后，通过分析项目计划过程中具有逻辑关系约束的活动间产生鲁棒性调度的要求，提出以项目活动延期风险权重大小和前置活动数量多少作为鲁棒性指标来合理分配时差；在第二部分建立了考虑活动延期风险权重加权时差的资源受限项目调度鲁棒性优化模型；第三部分设计了改进的基于禁忌搜索的模拟退火算法；第四部分是算例对比分析，并在最后提出了该问题的进一步研究方向。

1问题描述

项目调度的鲁棒性有两种情况：质量鲁棒性和解鲁棒性[1]。至于质量鲁棒性与解鲁棒性的权衡是根据项目的性质及项目决策者的偏好而定。本文以项目调度的质量鲁棒性为研究对象，即使项目活动的实际开始时间比计划开始时间延迟了些，只要不影响项目的完工时间都认为是鲁棒性的调度。要产生资源受限项目鲁棒性的调度，如何合理的分配时差是核心问题。本文从项目计划过程中具有逻辑关系约束的活动间产生鲁棒性调度的要求出发，据此寻求时差分配的原则。

1.1考虑时序关系约束的时差分配

文献[8,9]在考虑了项目活动的先后逻辑关系后，提出∑Si*NDSi的鲁棒性度量方式，其指标是将时差分配给紧后活动数量多的项目活动，依据是紧后活动数量越多的项目活动受到外界干扰后越可能影响其它的活动，推迟它们的完工时间，从而更有可能影响整个项目的完工日期，所以应使紧后活动数量多的项目活动得到时差的保障。但是在项目实际执行过程中，即使充分保证了紧后活动数量多的项目活动的稳定性，也不能保证其紧后活动不受外界干扰，若将时差都分配给了紧后活动数量多的项目活动，一旦那些紧后活动受到干扰将必然影响整个项目的工期。反之，若将时差分配给前置活动多的项目活动，即将时差置于各活动之后使时差得到共享，这样，时差才能流向真正需要的项目活动，保证时差得到充分有效的利用，基于此本文将上述度量方式中的紧后活动数量(total number of direct successors of activityi,NDSi)改为前置活动数量(total number of predecessors of activityi,NPi)。

假设某一项目由四个按先后顺序进行的活动组成，合同截止工期T=15，资源限量R=5，各活动的工期和资源需求量等参数如表1所示。如果以∑Si*NDSi为度量目标，则得到的最优调度方案如图1(a)、(b)、(c)所示。以图1(a)为例，将时差分配给紧前活动数量多的项目活动1，这样一来，在项目实际执行过程中，2天的时差只能被活动1所使用，一旦活动1的后置活动2、3、4受到不确定因素的干扰，将直接影响项目的工期，造成项目不能按时完成，也就是说该调度方案的抗干扰能力差，即鲁棒性差。如果以改进的∑Si*NPi为度量目标，则得到的最优调度方案如图1(d)所示，将时差分配给前置活动数量多的项目活动4，则在项目实际执行过程中，活动4受到干扰可利用此时差，活动1受到干扰同样可以使用此时差，而且能满足该项目在截止期限内完工，所以此调度结果是鲁棒性的，同理活动2、3也能利用此时差，也就是说这种调度方案产生的时差能用于所有的项目活动，使时差在实际执行过程中真正流向了需要的活动，在项目活动受到干扰时具有很强的抵抗风险的能力，调度结果鲁棒性强。因此本文将鲁棒性指标改为∑Si*NPi。图1为不同时差分配下的调度方案，各调度方案对比分析结果如表1所示。

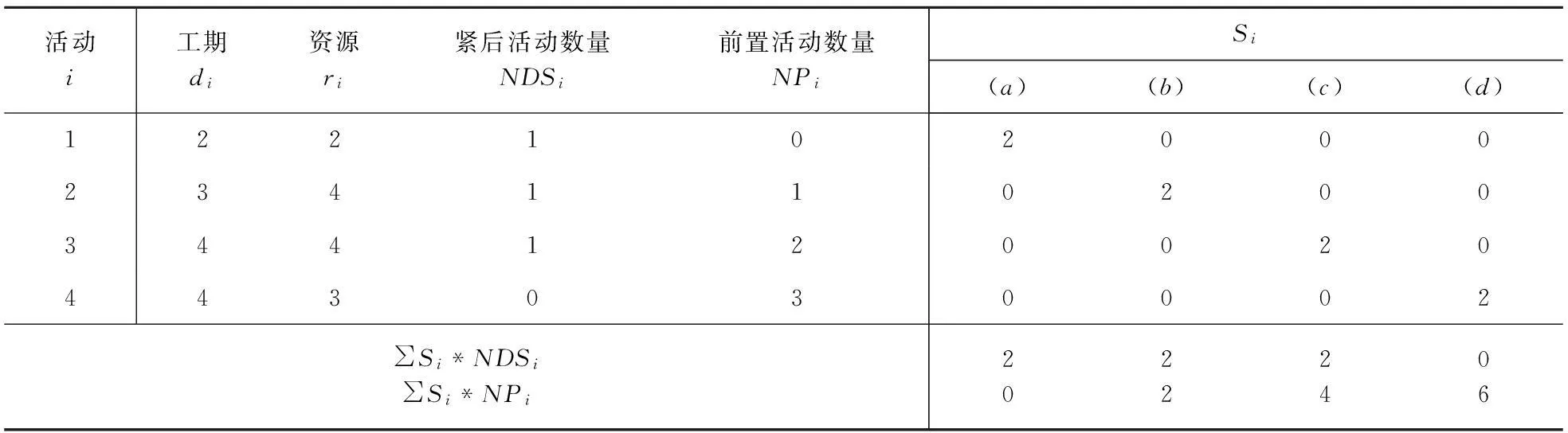
表1　项目一各活动参数及计算结果

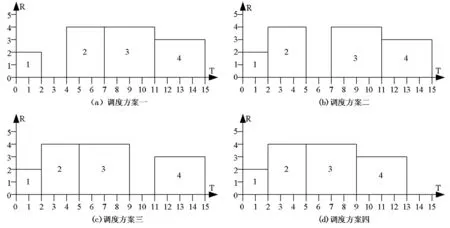
图1　项目一不同时差分配下的各调度方案

1.2考虑延期风险权重的时差分配

文献[10]提出了依据不稳定的活动权重来分配自由时差的思想，其权重是指活动受干扰影响的成本，其鲁棒性指标为∑Wi|E(Si)-Si|，该指标产生的调度结果具有解鲁棒性。文献[11]在研究资源约束下的突发事件应急救援鲁棒性调度优化问题时，将鲁棒性定义为各活动的时间缓冲与其权重系数乘积的总和，即RM=∑λnΔSn。文章指出各救援活动在应急救援过程中所处的位置及面临的内外环境不同，对于计划稳定性的影响程度也不可能完全相同，为此给每个救援活动定义了一个权重系数λn来测度其对于计划稳定性的重要性。

由于项目各活动的性质不同，当考虑活动的延期风险时，各活动的延期风险权重不可能完全相同，延期风险权重越大的活动越有可能影响项目的完工时间，因此在项目具有时差的情况下，应优先将时差分配给延期风险权重大的活动，这样就使得最可能影响项目工期的活动有了时差的保证，从而在项目的实际执行过程中有效抵抗来自不确定因素的干扰，即项目调度具有鲁棒性。因此在1.1部分提出的指标∑Si*NPi的基础上，进一步将指标定义为∑Wi*Si*NPi，这里的Wi为各活动的延期风险权重。

2鲁棒性度量方式的模型构建

根据1中问题的描述，假定一个含有N项活动的项目(i∈N,i=1,2,…,N)，活动j为活动i的紧后活动，Ui为活动i的所有紧后活动的集合(j∈Ui)，项目交货期为T，共需K种可再生资源。活动i对第k种资源的需求量为rik，单位时间内第k种可再生资源可用量为Rk，各活动的工期和延期风险权重分别为di和Wi，活动的前置活动数量记为NPi，设

考虑延期风险权重加权时差的资源受限项目调度鲁棒性度量方式模型为：

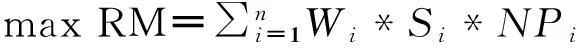
(1)

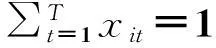
(2)

(3)

(4)

xit∈{0,1},∀i,t

(5)

其中，式(1)为目标函数，即以加权时差最大化为目标；式(2)用以保证各项目活动在计划工期内当且仅当在某一时间完成；式(3)表示项目各活动间的优先约束关系；式(4)用以保证每一时刻使用的可更新资源量约束；式(5)表示变量的取值范围。

3基于禁忌搜索的模拟退火算法设计

资源受限项目调度问题已被证明为NP-hard问题[12]。模拟退火(Simulated Annealing, SA)算法是一种对NP-hard问题寻优求解非常有效的算法[6]。由鲁棒串行生成机制[13]产生的初始解和可行解具有较强的随机性，因此本文采用禁忌搜索算法获得初始解，这样在随后的模拟退火算法最终寻优过程中能高效快速地得到最优的鲁棒性调度解。

(1)禁忌搜索算法产生鲁棒初始调度

初始化从优化结果O*开始的迭代it及迭代次数，设置将工期最小为目标所产生的调度作为初始解，滞空禁忌表，由此生成当前解的领域解，并在领域Ⅰ和Ⅱ内根据自定义值nⅠ和nⅡ进行搜索选出候选解，将满足活动逻辑关系的解作为当前解，用其对应的对象替换最早进入禁忌表中的对象，更新最优解，直至满足终止准则(工期

禁忌搜索算法步骤如下：

令L*=L,B*=B, O*=O,T=n,it=0, itnoimprove=0

While (工期

for n=1 to nⅠdo：

令O=-999999, it=it+1

for i=2 to n-2, for j=i+1 to n-1 do:

如果满足活动逻辑关系则交换Li和Lj

if(O>O*and Sn≤δn)or(O=f(B,L)>O′ and it>tabuLi,SLiand it>tabuLj, SLj)

then store i→i′, j→j′, O→O′

如果不满足活动逻辑关系未交换

if ∃i′ and ∃j′

then交换Li′和Lj′,tabuLi′,SLi′=tabuLj′,SLj′=it+T

if O′> O*and Sn<δn

then O*=O′ , L*=L, itnoimprove=0

else itnoimprove=itnoimprove+1

for n=1 to nⅡdo：

令O′=-999999, it=it+1, Δbased on itnoimprove

for i=2 to n-1, for b=-Δ to Δ do：

if Bi+ b > 0

then Bi=Bi+b

if(O>O*and Sn≤δn)or(O=f(B,L)>O′and it>tabui,Bi)

then store i→i′, b→b′, O→O′

else

if ∃i′ and ∃b′

then Bi=Bi+b′, tabui,Bi=it+T

if O′>O* and Sn<δn

then O*=O′, B*=B, itnoimprove=0

else itnoimprove=itnoimprove+1

(2)模拟退火算法寻求最优的鲁棒性调度

在算法寻优过程中，以鲁棒性指标RM最大为目标函数，从而保证项目鲁棒性最大目标的实现，用(1)禁忌搜索产生的优解作为当前解S0，并产生领域解Sn，根据Metropolis准则接受新解，它除了接受优化解外，还在一定限度内接受恶化解，以保证下一个温度的搜索不会遗漏较优解，但随着温度t的减小，就只能接受较少的恶化解，最后在T值趋于零时，就不再接受恶化解了，从而最终得到全局的最优解。

模拟退火算法所用到的符号如下：

T0：初始温度，该温度应越高越好，以减少接受最差解的可能性

L：马尔科夫链长

S*：最优解

RM(S)：鲁棒性度量方式评价函数

P：当领域解不比现行解优时接受它的可能性

模拟退火算法步骤如下：

初始化SA的控制参数(T0，L)

选择一个初始解，S0

令T=T0,S=S0,S*=S0；计算RM(S0)；

While T>Tmindo:

n=1;

While n

产生S0的领域解Sn;计算Δ=RM(Sn)-RM(S);

if Δ≤0

S=Sn

else

产生一个随机数，r∈(0,1);

if(r≤p=e-Δ/T);

S=Sn; n=n+1;

end

end

if RM(S*)≤RM(S)

S*=Sn;

end

end

温度T衰减；

end

4算例分析

本文引用文献[10]所采用的算例进行研究。该算例的单代号网络图如图2所示，该项目共有10个活动，活动1和活动10为虚活动，图中节点上的数字分别表示该活动的工期di、资源需求量ri和权重Wi，资源限量R=8，截止期限T=18。各活动的参数如表2所示。

图2　项目二的单代号网络图

活动i工期di资源ri权重Wi权重归一化紧后活动数量NDSi前置活动数量NPiSi(a)(b)(c)(d)222150.2344100000373100.1563100110434110.1719110000544120.187520012068390.140602320576210.015601010784310.015611011092450.0781023101鲁椿性指标∑var(αi)0.2390.0230.0290.163∑Si*NDSi0460∑Wi*Si*NPi1.3120.7490.0161.671

对于该算例，不同优化指标得到的不同最优调度方案如图3 所示。初始调度方案是以工期最短为目 标函数所产生的调度方案，如图3(a) 所示; 文献[8，9]中提到的以NDSi 作为度量方式所产生的 调度方案如图3(b) 所示，是以指标值最大作为鲁棒性最大化的标准; 文献[13]调度方案是以所有活动比 值αi 的均方差总和，即ΣVar(αi)作为鲁棒性的度量方式，文章指出该指标值越小，表明活动的鲁棒性 随活动工期的分布越合理，如图3(c) 所示; 本文以作为鲁棒性的度量方式产生的调度方 案如图3(d) 所示，该鲁棒性指标值越大则鲁棒性越强。由表2 中数据可以看出，在上述不同的度量指标 下所得到的最优调度方案有所不同，采用本文提出的以活动延期风险加权时差为鲁棒性度量指标(= 1．671) 的调度方案为最优调度方案。

为衡量比较各调度方案的抗干扰能力，综合活动延期风险权重和前置活动数量两方面的因素，假设活动4、6、7、9受到不确定因素的干扰，活动工期将会延长，其额外增加的工期分别设为1、1、2、1，其余活动工期不变。受干扰后项目调度变化情况如图4所示。由图4中可以看出，在受到干扰后，各方案的项目工期都有所变化，(a)、(b)、(c)调度方案工期都增加为19天，超过了项目的截止工期，而本文调度方案(d)工期为18天，即在截止日期内正好完工。从对比分析结果可以看出，由本文鲁棒性指标所产生的调度方案较其他各优化调度方案具有更高的风险抵抗能力，从而验证了本文所提鲁棒性指标的有效性和优越性。

图4　各调度方案受干扰后的变化情况

5结论

针对活动间具有逻辑关系的资源受限项目调度问题，将时差按前置活动数量及延期风险权重来分配，保证了前置活动数量多、延期风险权重大的项目活动的鲁棒性，这样有利于抵抗外界干扰因素的影响，使得项目具有很好的质量鲁棒性。由此提出了基于前置任务数量和活动延期风险加权时差的资源受限项目调度鲁棒性指标及相应的优化模型，并设计了基于禁忌搜索的模拟退火算法，改进的算法能更有效率地寻得最优鲁棒调度解。最后通过算例对比分析各不同鲁棒指标的调度方案，及受干扰后项目的稳定性，验证了该度量方式的有效性与优越性，同时也验证了本文所设计的基于禁忌搜索的模拟退火算法的合理性和有效性。由于本文活动延期风险权重是直接给定的，而在实际中则需要用一定的科学方法来确定，所以活动延期风险权重的确定问题将会是另一个有价值的研究方向。

参考文献：

[1]Al-Fawzan M A, Haouari M. A bi-objective model for robust resource-constrained project scheduling[J]. International Journal of Production Economics, 2005, 96(2): 175-187.

[2]Van De Vonder S, Demeulemeester E, Herroelen W, Leus R. The use of buffers in project management: the trade-off between stability and makespan[J]. International Journal of Production Economics, 2005, 97(2): 227-240.

[3]Van De Vonder S, Demeulemeester E, Herroelen W, Leus R. The trade-off between stability and makespan in resource-constrained project scheduling[J]. International Journal of Production Research, 2006, 44(2): 215-236.

[4]Van de Vonder S, Ballestin B, Demeulemeester E, Herroelen W. Heuristic procedures for reactive project scheduling[J]. Computers & Industrial Engineering, 2007, 52(1): 11-28.

[5]王勇胜,梁昌勇.资源约束项目调度鲁棒性研究的现状与展望[J].中国科技论坛,2009,(8):95-99.

[6]Abbasi B, Shadrokh S, Arkat J. Bi-objective resource-constrained project scheduling with robustness and makespan criteria[J]. Applied Mathematics and Computation, 2006, 180(1): 146-152.

[7]Kobylanski P, Kuchta D. A note on the paper by M. A. Al-Fawzan and M. Haouari about a bi-objective problem for robust resource-constrained project scheduling[J]. International Journal of Production Economics, 2007, 107(2): 496-501.

[8]Chtourou H, Haouarib M. A two-stage-priority-rule-based algorithm for robust resource-constrained project scheduling[J]. Computers & Industrial Engineering, 2008, 55(1): 183-194.

[9]Khemakhem M A, Chtourou H. Efficient robustness measures for the resource-constrained project scheduling problem[J]. Int. J. Industrial and Systems Engineering, 2013, 14(2): 245-267.

[10]Lambrechts O, Demeulemeester E, Herroelen W. A tabu search procedure for developing robust predictive project schedules[J]. International Journal of Production Economics, 2008, 111(2): 493-508.

[11]胡信布,何正文,徐渝.基于资源约束的突发事件应急救援鲁棒性调度优化[J].运筹与管理,2013,22(2):72-79.

[12]Blazewicz J, Lenstra J K, Kan A H G R. Scheduling subject to resource constraint: classification and complexity[J]. Discrete Applied Mathematics, 1983(5): 11-24.

[13]庞南生,孟俊姣.多目标资源受限项目鲁棒调度研究[J].运筹与管理,2012,21(3):27-32.