离差最大化时基于交叉评价的多属性决策方法

离差最大化时基于交叉评价的多属性决策方法

郭清娥，苏兵

(西安工业大学经济管理学院,陕西西安710032)

摘要：针对属性权重完全未知，且评价系统内既有客观数据、又有主观因素的多属性决策问题，提出一种基于离差最大化和交叉评价的模糊多属性决策方法。该方法首先定义了最小交叉效率、最大交叉效率等概念，将量化指标用交叉评价方法进行处理；然后采用模糊综合评价方法评价非量化指标，并基于离差最大化思想确定权重；最后将模糊化处理之后的量化指标与非量化指标一起进行最终评价，建立离差最大化条件下基于交叉评价的模糊多属性决策模型。最后通过算例验证了方法的可行性及有效性。

关键词：运筹学；交叉评价；模糊综合评价；离差最大化；模糊多属性决策

收稿日期：2014-03-18

基金项目：国家社会科学基金资助项目(13BGL156)；陕西高校人文社科青年英才支持计划；西安工业大学校长科研基金资助项目(XACDXJJ14016)

作者简介：郭清娥(1981-)，女，湖北襄阳人，博士，研究方向：项目评价与决策；苏兵(1970-)，女，山西大同人，教授、博士，研究方向：突发事件与应急决策。

中图分类号：C934 文章标识码：A

Fuzzy Multi-attribute Decision Making Method Based on Maximizing

Deviation and Cross-Evaluation

GUO Qing-e, SU Bing

(SchoolofEconomicsandManagement,Xi’anTechnologicalUniversity,Xi’an710032,China)

Abstract:Considering the multi-attribute decision making problem with both quantitative data and non quantitative index, in which the information about attribute weights are unknown completely, a method based on maximizing deviation and cross-evaluation is introduced. First we calculate the “average cross-efficiency evaluation”, “minimum cross-efficiency evaluation”, “maximum cross-efficiency evaluation” using the cross-evaluation model; then use the fuzzy comprehensive evaluation model to deal with the non quantitative index; finally we evaluate the quantitative data and non quantitative index together. The weight of every decision unit is determined by the maximizing deviation method. And an example is given to illustrate the effectiveness of the method proposed.

Key words:operational research; cross-evaluation; fuzzy comprehensive evaluation; maximizing deviation; fuzzy multi-attribute decision making

0引言

由于客观事物的复杂性、不确定性以及决策者认知水平的有限性，加之多属性决策中，往往既有客观数据，又有各种主观因素，对于决策者来说，要立刻对评价对象做出精确的评判，是非常困难甚至是不可能的。数据包络分析(DEA)可以通过对客观数据的分析和计算得出评价单元的相对效率，而模糊综合评价(FCA)则可由专家对主观因素进行模糊变换取得综合评价向量，因此学者们提出了将DEA和FCA相结合的综合评价方法来解决客观数据与主观因素并存的多属性决策问题。文献[1～5]将DEA决策单元的输入输出考虑为模糊数，考虑如何向确定型DEA模型的转化，并讨论了有效性问题。这些研究本质上是将模糊数学引入到数据包络分析中，是基于模糊数学的数据包络分析，属于“模糊DEA”，并没有充分利用模糊综合评价的易操作性。为使两者更好地结合，文献[6～8]做了进一步的研究。其中文献[8]的工作具有代表性，他将评价系统内的量化指标采用数据包络分析方法得到各评价单元的相对效率，再进行模糊化处理，并与非量化指标一起进行模糊综合评价。此方法用数据包络分析的优化结果代替专家评分，使模糊综合评价更具说服力。

上述模型均采用普通数据包络分析(DEA)方法建模，但DEA模型存在一定缺陷。它是建立对决策单元最有利的模型，最优解为决策单元可能相对效率的最大值，具有“夸大自身优势，回避劣势”的特点，不够客观和全面。为了解决这一问题，近年来许多学者开始研究交叉评价在多属性决策中的应用[9～13]。值得一提的是文献[9]，在文献[8]的框架下，考虑到传统DEA模型的缺陷及传统DEA处理结果为单一数值，客观上不具备模糊综合评价所需要的隶属度，将DEA交叉评价的处理结果通过特定方式模糊化为三角模糊数，使DEA交叉评价和模糊综合评价有机结合在一起，建立了更具客观说服力的模型。

本文是在文献[9]的框架下进行分析的。文献[9]中，非量化各指标的权重设定为已知，量化指标和非量化指标的比重也由决策者提前给出。而在现实问题中，准确获知各指标的权重并非易事，人为指定又主观色彩过于浓厚。本文考虑到实际情况，在文献[9]的基础上进行了改进。这种改进主要体现在假定各属性权重完全未知的情形下，借鉴离差最大化思想，提出一种基于离差最大化和交叉评价的模糊多属性决策方法，以使模型能更客观和全面地反映现实系统。

1相关知识回顾与分析

1.1DEA交叉评价

记DEA评价系统中第i个决策单元为DMUi，其输入、输出向量分别为：Xi=(xi1,xi2,…,xis)T，Yi=(yi1,yi2,…,yip)T。各自对应的权重向量分别为：νi=(νi1,νi2,…,νis)，ui=(ui1,ui2,…,νip)。

文献[14]已经给出了DEA交叉评价的步骤。这里结合文献[14]，首先给出如下概念：

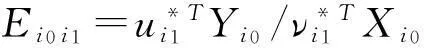
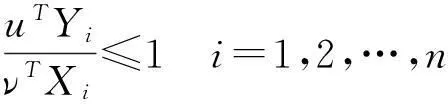
(1)

uk≥0,k=1,2,…,p

νj≥0,j=1,2,…,s

交叉效率Ei0i1表示当采用决策对象DMUi1的最有利权重时，决策对象DMUi0的相对效率。即DMUi1对DMUi0的效率评价值。

定义2称所有决策单元对DMUi0交叉效率的平均值为DMUi0的平均交叉效率，记为：

(2)

定义3[9]称所有决策单元对DMUi0交叉效率的最小值为DMUi0的最小交叉效率，记为：

(3)

定义4[9]称所有决策单元对DMUi0交叉效率的最大值为DMUi0的最大交叉效率，记为：

(4)

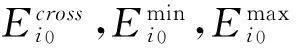
1.2离差最大化方法决策原理

(5)

(6)

(7)

构造Lagrange乘子函数

令

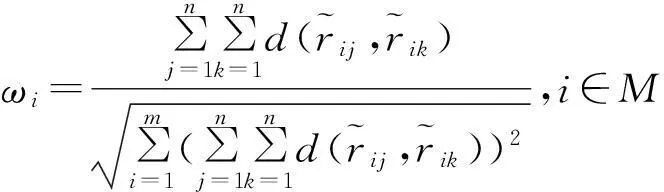
对上述权重向量作归一化处理得

(8)

2离差最大化条件下基于交叉评价的模糊综合多属性决策方法

本文提出的离差最大化条件下基于交叉评价的模糊综合多属性决策方法的基本思路是，将交叉评价的结果(最小交叉效率、平均交叉效率和最大交叉效率)进行模糊化处理后作为模糊综合决策时的指标进行评价，各属性权重由离差最大化的思想进行确定。基本步骤如下：

Step 1将评价系统内所有指标因素分为量化指标和非量化指标。

图1　量化指标模糊化后的隶属函数

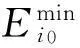
Step 4运用模糊综合评价法来计算非量化指标。将评语集V划分为ν1，ν2，ν3，ν4，ν5这样5个等级。评语集与隶属函数的对应关系见表1：

表1　评语集和隶属函数对应关系

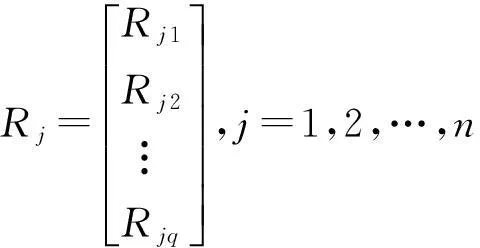
Step 6将Step3模糊处理后的量化指标与经Step5计算后的非量化指标进行综合评价。

和文献[9]不同，此处量化指标和非量化指标比重完全未知。由式(6)、(7)、(8)，参照步骤5，仍然由离差最大化方法来求解权重。

Step 7根据三角模糊数的期望公式，由期望值对各决策单元进行评价。

3应用算例

对8个实验室进行评估。评价指标分为量化与非量化指标两部分，其中人力财力是量化指标，综合管理为非量化指标。具体指标及相应数据如表2所示(人力财力部分数据来源于文献[8])。表中，一级指标包括人力财力和综合管理，二级指标包括人数(输入,单位为个)、资金投入(输入，单位为万元)和委托检验投入(输出，单位为万元)；运行管理、实验科研、资源共享。各指标权重完全未知。

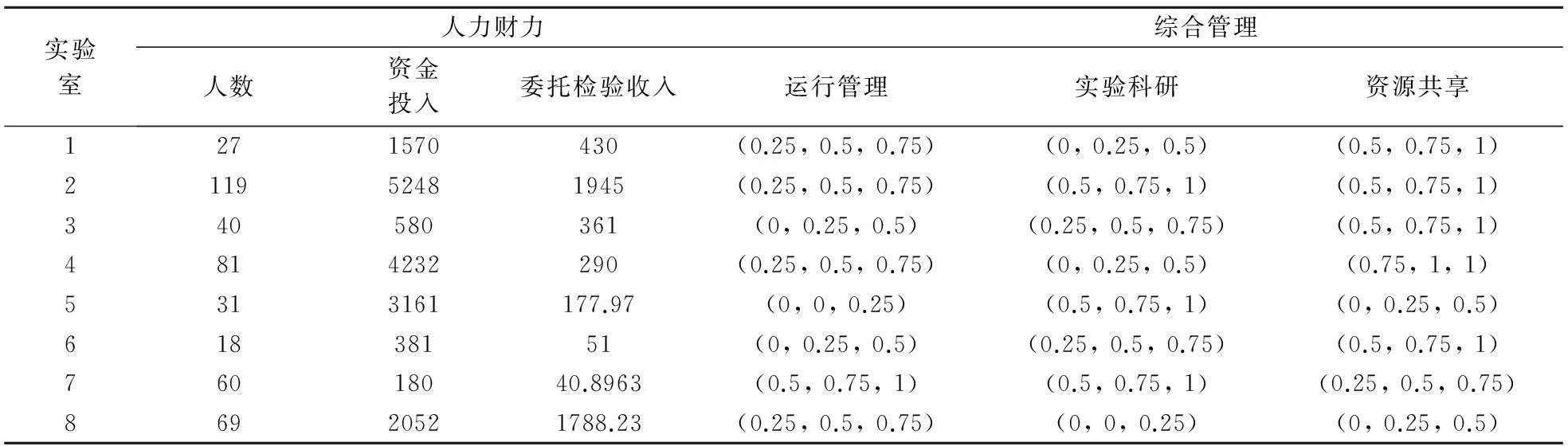
表2　各实验室统计数据

采用本文离差最大化条件下基于交叉评价的模糊多属性决策方法进行分析。首先求得各拟评价实验室的量化指标(人力财力)的最小交叉效率值、平均交叉效率值及最大交叉效率值分别为：

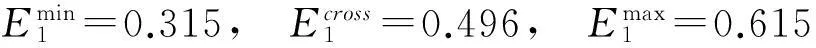
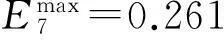
按照本文第3部分的步骤3对交叉效率值进行模糊化处理。可以得到表3所示交叉效率值模糊化隶属度。

表3　量化指标处理结果

对运行管理、实验科研、资源共享按照非量化标处理过程进行计算。其中非量化指标综合管理的评语集为：V=(很差，差，一般，好，很好)，各自对应的隶属函数见表1。根据评语集和隶属函数的对应关系，非量化指标的综合评价矩阵如表2右半部分所示(此处评价数据来自文献[9])。

由式(6)和(7)将上述矩阵转化为规范化矩阵如表4所示：

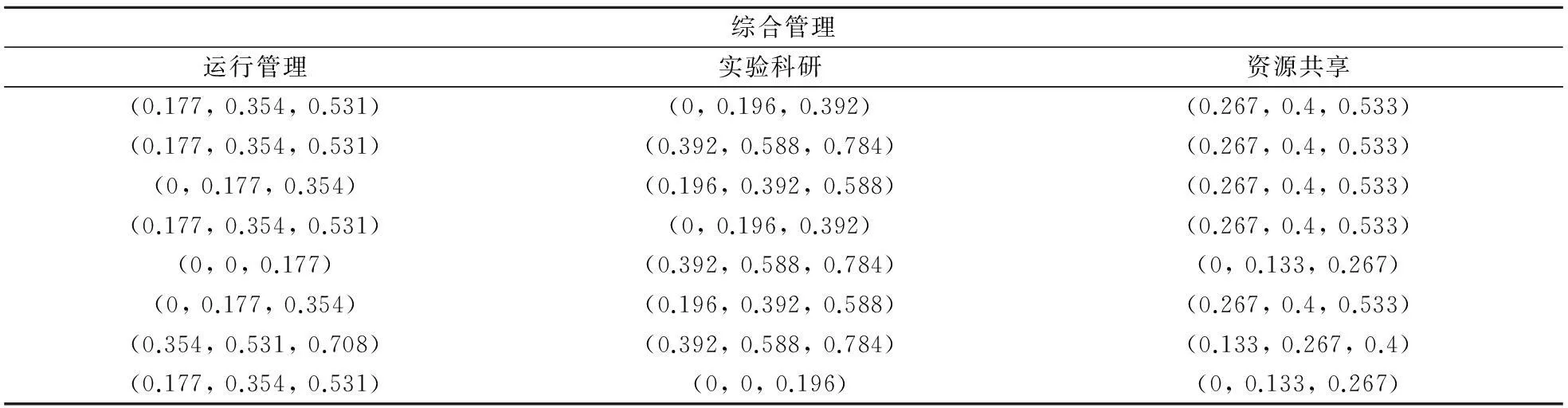
表4　非量化指标评价规范化矩阵

利用式(8)求得非量化指标(综合管理)三个分指标权重分别为：0.313，0.435，0.252。带入得加权规范化矩阵即为非量化指标最终处理结果。

表5　非量化指标最终评价隶属函数

结合表3最后一列量化指标处理结果和上表非量化指标处理结果，再重复上述步骤，按照公式(6)和(7)规范化，求得量化指标与非量化指标权重为0.65，0.35。

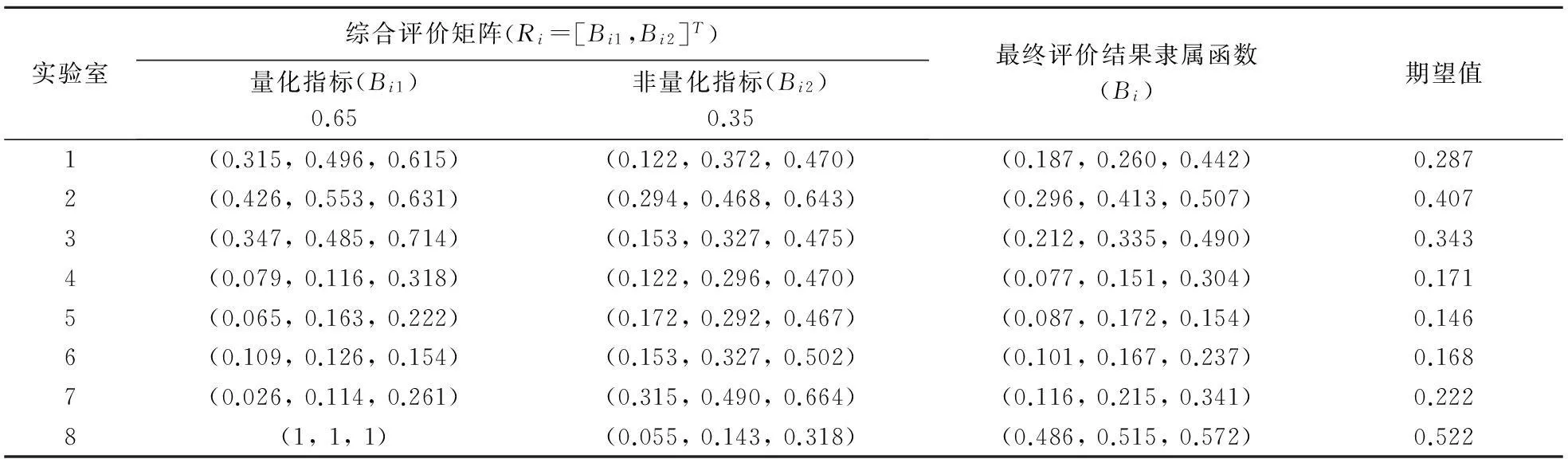
表6　 最终综合总评结果

根据三角模糊数的期望公式，选择最终评价结果Bj的期望值作为最终的评价决策依据。按最终评价结果的期望值，各实验室从优到劣依次为8，2，3，1，7，4，6，5，最佳为实验室8。

4结论

本文针对评价系统内既有客观数据，又有主观数据，且属性权重完全未知的情况，给出了处理方法。将量化指标用DEA交叉评价方法处理，并将之模糊化；非量化指标采用模糊综合评价，最后再一起进行最终评价。引入离差最大化方法确定各属性的权重。该方法充分避免了由决策人员人为指定权重造成的主观性，使最终结果更加合理。

参考文献：

[1]彭熠.基于多目标规划的模糊DEA有效性[J].系统工程学报，2004，19(5)：548-552.

[2]Mei L W, Huai S L. Fuzzy data envelopment analysis(DEA): model and ranking method[J]. Journal of Computer and Applied Mathematics, 2009, 223(2): 872-878.

[3]Mohamed D. A model of fuzzy data envelopment analysis[J]. Information Systems and Operation Research, 2004, 42(4): 267-279.

[4]丁德臣，龚艳冰，何建敏.基于模糊C-OWG算子的模糊DEA模型求解[J].模糊系统与数学，2009，23(2)：131-135．

[5]廖东升，沈永平，陈英武等.基于模糊综合评价的DEA方法在心理战评估中的应用研究[J].运筹与管理，2008，17(1)：131-136．

[6]段绍伟，沈浦生.模糊综合评价与数据包络分析在工程方案设计选择中的应用[J].水利学报，2004，5(5)：116-121．

[7]张熠，王先甲.基于数据包络分析和模糊理论的投资项目评价方法研究[J].技术经济，2010，29(2)：64-67．

[8]柳顺，杜树新.基于数据包络分析的模糊综合评价方法[J].模糊系统与数学，2010，24(2)：93-98．

[9]郭清娥，王雪青，位珍.基于DEA交叉评价的模糊综合评价模型及其应用[J].控制与决策，2012，27(4)：575-578.

[10]刑会歌，王卓甫，尹红莲.基于DEA的决策单元排序方法研究[J].系统工程与电子技术，2009，31(11)：2648-2651．

[11]王金祥.基于超效率DEA模型的交叉效率评价方法[J].系统工程，2009，27(6)：115-118．

[12]王洁方，刘思峰.基于交叉评价和竞争视野优化的多属性决策方法[J].控制与决策，2009，24(10)：1495-1503．

[13]黄宗盛，胡培，聂佳佳.基于离差最大化的交叉效率评价方法[J].运筹与管理，2012，21(6)：177-181．

[14]Sexton T R, Silkman R H, Hogan A J. Data envelopment analysis: critique and extensions[M]. San Francisco: Jossey Bass, 1986.

[15]Chen C T. Extensions of the TOPSIS for group decision-making under fuzzy environment[J]. Fuzzy Sets and Systems, 2000, 114(1): 1-9．

[16]吕翔昊，李登峰.基于模糊信息的群体多维偏好分析决策模型[J].系统工程与电子技术，2004，26(5)：605-607．

[17]王洁方，刘思峰，刘牧远．不完全信息下基于交叉评价的灰色关联决策模型[J]．系统工程理论与实践，2010，30(4)：732-737．