博弈方的行动集合变化的博弈运动研究——以稀土出口贸易为例

博弈方的行动集合变化的博弈运动研究——以稀土出口贸易为例

徐寅峰1,2,文生威

(1.四川大学商学院，四川成都610065；2.机械制造系统工程国家重点实验室，陕西西安710049)

摘要：文章以稀土出口贸易为背景，分析了博弈方的行动集合随时间变化的博弈运动。首先定义了行动集合的三种变化情形：集合变大、集合变小和集合变化不确定。然后针对单个博弈方行动集合的三种变化情形，分别讨论了均衡解的运动轨迹，分析表明：在行动集合变大和变小两种情形下，均衡解的轨迹呈现互逆的运动特性；在行动集合变化不确定的情形下，保守和冒险策略等价，固定策略严格优于保守、冒险策略。在此基础上，将模型推广到博弈双方的行动集合均发生变化的博弈运动模型，分析表明上述结论仍然成立。最后，以中国同马来西亚在2012年6月到2013年3月间的稀土出口贸易为例，验证了本文模型和求解方法的合理性与可行性。

关键词：稀土贸易;寡头竞争;行动集合;博弈运动;运动轨迹

收稿日期：2013-07-14

基金项目：国家自然科学基金资助项目(71371129,61221063);长江学者和创新团队发展计划(IRT1173)

作者简介：徐寅峰(1962-)，男，吉林人，教授，研究方向：运筹与控制；文生威(1987-)，男，河南人，硕士研究生。

中图分类号：F224文章标识码：A

Research on the Gaming of the Players’ Action Sets Changing:

A Case Study of the Rare Earth Trade

XU Yin-feng1,2, WEN Sheng-wei

(1.BusinessSchoolofSiChuanUniversity,Chengdu610064,China; 2.StateKeyLabforManufacturingSystemsEngineering,Xi’an710049,China)

Abstract:Considering the export of rare earth as background, this paper analyzes the gaming model in which the players’ action sets are changing over time. First, we define three changing styles for action set: action set heightening, action set shrinking, and action set changing indeterminacy. Then we investigate the track of the equilibrium solution in which only one player’s action set will change over time. The results show that the tracks of the equilibrium solution when the action set heightening and shrinking are opposite, and the stationary strategy is strictly superior to conservative strategy and risky strategy which are equivalent in this situation. Moreover, this single action set changing model is applied to both two action sets changing over time and the results still hold trne for the new model. Finally, the rationality and feasibility of the gaming model and solution are validated by a case study of the rare earth export of China and Malaysia from June 2012 to March 2013.

Key words:rare earth trade; oligopoly competition; action sets; gaming; motion trial

0引言

一般认为对博弈论的研究开始于Zermelo和Neumann等人。1913年，Zermelo提出了选择公理[1]。1928年，Neumann证明了最大最小定理，标志着博弈论的正式诞生[2]。1944年，Neumann和Morgenstern合著《Theory of games and economic behavior》，将两人博弈模型推广到N人博弈并系统地应用于经济领域，构建了博弈论的理论体系[3]。1951年，Nash提出和论述了纳什均衡的概念，奠定了非合作博弈的理论基础[4]。1966年，Selten深入研究了动态博弈中策略的交互作用，提出子博弈精炼纳什均衡，随后，Aumann和Maschler建立了不完全信息的重复博弈模型[1]。1973年，Smith和Price将生物理论中的进化思想引入到博弈论中，提出了演化博弈的思想和演化稳定策略的概念[5]。除此之外，还有许多国内外学者的研究工作对博弈论的发展起到推动作用。现今，博弈论已经成为经济学和管理学的核心内容。

通常情况下，把以Nash为代表的博弈论称为经典博弈论，经典博弈论假设博弈结构和环境在博弈发生前事先给定。然而在现实的世界中，信息、物质、能量处于一个快速变化的过程中，人类世界信息量的增加、自然环境和社会环境的运动变化导致博弈的各要素处于变化之中。博弈方、行动集合、博弈次序和得益函数等要素在博弈的过程中发生变化，博弈不是在静态的环境和固有的结构下进行的，而是在运动发展的环境和结构中进行的，称这种运动变化的博弈为博弈运动(Gaming)。它不是某些博弈简单的重复或交替，而是考虑博弈要素随时间运动变化。社会经济活动中的博弈运动现象有很多，例如国际稀土贸易活动就是一个典型的博弈运动。长期以来，中国的稀土出口量在国际稀土贸易总量中占90%的比重[6]。2013年1月，稀土生产商Lynas宣布在马来西亚建设稀土提炼厂，该厂竣工后将是世界最大的稀土提炼厂。随着马来西亚稀土产量的变化，该国的行动集合也随之发生变化，那么，中国同马来西亚的稀土出口博弈具有博弈运动的特征，随着这种运动变化，国际稀土市场的贸易格局将发生重大转变，研究各国如何在这种新形势下进行稀土出口博弈具有一定的理论和现实意义。

目前，从博弈论的角度对稀土出口的研究还比较少，并且都是从经典博弈论出发的。王正明等[7]从税收转嫁的角度分析了寡头国家的稀土资源税对出口市场势力的影响，研究了市场出清条件下的价格转移弹性。裴文琳等[8]利用灰色关联度模型评估稀土出口总量分别对出口价格、进口价格、进口总量的相关程度, 提出了我国稀土贸易的相关建议。本文从博弈运动的角度对稀土贸易的寡头市场进行分析，讨论行动集合变化的稀土出口寡头博弈。国内外有不少学者从不同的角度对寡头模型进行了研究，Elsadany[9]和Agiza[10]从动态博弈的角度讨论了企业序贯博弈和有限理性等因素对博弈方的影响，给出了相应情形下动态模型的决策值。卢亚丽[11]和闫安等[12]从系统动力学的角度分析了寡头竞争的均衡解，并分析了系统的稳定性。Mallard[13]从演化博弈的角度出发，探讨了有限理性在的产量调整过程中所起的作用，并从环境与组织本身的影响因素出发，研究了学习型企业的动态调整策略。此外，廖萍康[14]、Anufriev[15]和Zschocke[16]等学者放宽原模型的条件对寡头模型进行了研究。这些文献的研究工作对博弈论的发展起到积极的作用，可是尚未考虑行动集合随时间变化的情形，也不满足行动集合的变化不改变均衡解的隐含条件。本文考虑行动集合这一个因素发生变化的博弈运动模型，从运动变化的角度研究稀土出口博弈，讨论了均衡状态的运动形式和博弈方的行动选择，这是以往文献没有研究过的，也是本文的创新点和价值所在。

1问题的描述与模型的建立

定义3行动集合变化的博弈运动模型为G(t)=[{A,B},{Sj(t)},{πj(t)}]，其中{A,B}表示博弈方的集合，t=0,1,2,…,T，j=1,2,j=1时表示博弈方A，j=2表示博弈方B，Sj(t)表示t时刻博弈方j的行动集合，πj(t)表示t时刻博弈方j在t时刻的收益。

定义4博弈运动的轨迹可以用相继的收益和实现该收益的行动选择组成，从初始时刻直到t时刻的轨迹记为H(t)=(q1(0),q2(0),π1(0),π2(0);q1(1),q2(1),π1(1),π2(1);…;q1(t),q2(t),π1(t),π2(t))，将这种记录博弈方的行动选择和收益的序列称为0到t时刻的运动轨迹。

H(t)是对整个博弈运动而言的，它包含从初始时刻直到t时刻的博弈运动信息，记录和反映了博弈方的行动和收益。特别的，当博弈方的策略是均衡策略时，H(t)可以反映均衡解的运动转移情况。当博弈方{A,B}的产能很大时，行动集合Sj(t)就很大，即为任意时刻博弈方的行动不受产能的制约，则模型G(t)=[{A,B},{S(t)},{π}]退化为寡头模型G0=[{A,B},{S},{π}]。本文考虑行动集合的变化是博弈运动模型G(t)与模型G0的主要不同。

2行动集合变化的博弈模型分析

(1)

博弈方B的收益函数为：

(2)

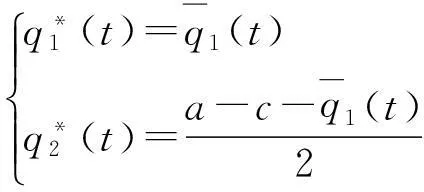
性质2在模型G(t)中，如果在t时刻博弈方A的产能小于模型G0均衡解，那么博弈方B不会同博弈方A联合。

(3)

(4)

令Δπj(t)表示t时刻博弈方j的产能信息未知时的收益减去其的产能已知时的收益，则有：

(5)

2.1行动集合逐渐变大

定理1在博弈运动模型G(t)中，如果满足S1(t)⊆S1(t+1)，那么博弈方B的决策值是从联合生产均衡状态向模型G0均衡状态的转移过程。

证明博弈方A的产能逐步增加且没有达到模型G0均衡解时，由性质1知A的决策值为其产能。当A的行动集合变大且已知时，则B的收益函数表示：

(6)

(7)

定理1表明：当稀土出口国A的产能和出口量逐步增加时，稀土出口国B的出口量不是稳定的，而是一个运动转移的过程，意味着B在每个时刻都要对出口量进行修正。B对出口量进行修正时依赖于A的行动集合的变化，分析B的决策可得以下推论：

推论1在博弈运动模型G(t)中，如果满足S(t)⊆S(t+1)，那么博弈方B采取保守策略将会促使博弈方A声明其行动集合。

(8)

可知B采取冒险策略时Δπ1(t)>0，A的收益增加；又因为Δπ2(t)<0，即只要B对A行动集合的大小的预估出现偏差，B的收益就会减少，所以B希望正确的估计A的产能。综上所述：B采取保守策略，这对A构成威胁并将导致A的收益减少，那么A为了避免收益的减少，将会声明其行动集合，使B可以观察到A的产能。证毕。

2.2行动集合逐渐变小

定理2在博弈运动模型G(t)中，如果S(t+1)⊆S(t)，那么博弈方B的决策值的转移过程是博弈方A的行动集合变大情形时的逆过程。

推论2在博弈运动模型G(t)中，如果满足S(t+1)⊆S(t)，那么博弈方B采取冒险策略将会促使博弈方声明其行动集合。

(9)

2.3行动集合变化情形不确定

定理3在博弈运动模型G(t)中，博弈方A行动集合变化情况不确定，则博弈方B采取保守策略和冒险策略等效，固定策略严格优于保守策略和冒险策略。

(10)

(11)

(12)

(13)

定理3表明：当博弈方A的行动集合变化情形不确定时，博弈方希望得到的均衡策略适用于任意一个可能初始产能。所以在实际的问题中，博弈方可能只需要知道在某些或者某一个特定情形下如何进行策略选择的就足够了，也就是说博弈方可以采取相对稳定的出口策略。

3模型进一步讨论

Step 1初始化并设置参数a,c,T,q1(0),q2(0)，计算π1(0),π2(0)，并令t=1；

Step 4计算t时刻的收益πj(t)；

Step 5更新H(t)。执行t:t+1，然后返回到step2。

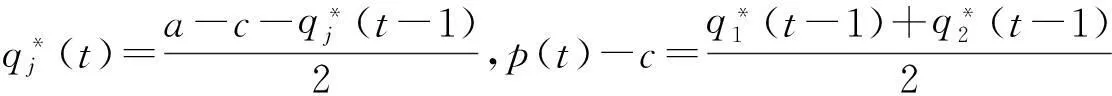
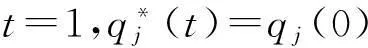
Step 4计算t时刻的收益πj(t)；

Step 5更新H(t)。执行t:t+1，然后返回到step 2。

4算例分析

依据统计数据，对模型参数进行赋值，通过算例来直观反映博弈双方行动集合都发生变化时的博弈运动模型。国际市场2012年稀土需求量约13万吨，平均每月需求量1.038万吨，出口成本大概21万元/吨。对数据进行预处理，A=1038(十吨)，C=210(万元/十吨)。另外2012年6月到2013年3月马来西亚和中国的稀土产能如表5-1，令2012年6月为博弈运动模型的初始时刻，有q1(0)=186.0，q2(0)=303.6，T=9，将这些参数作为初始输入，计算得π1(0)=57920.4，π2(0)=102948.8

有

H(0)=((186.0),(303.6)(57920.4)(102948.8))

然后进入t=1时刻，博弈方选择此时的出口量。依据冒险策略的计算步骤Step 3，可以得出马来西亚和中国采取冒险策略时的稀土出口量分别为

此时π1(1)=81501.0，π2(1)=59862.1，有

H(1)=((186.0),(303.6),(57920.4),(102948.8);(338.6),(248.7),(81501.0),(59862.1))

依次可以计算出直到T时刻博弈方的各期决策值，绘制表5-2。依据表5-2中博弈双方的决策值便可计算博弈方采取不同策略时各期的收益值，同时，可以得到运动轨迹H(t)。冒险策略下总收益分别为661898.6万元和703489.0万元。同样道理，依据保守策略计算方法可得双方的各期决策值和收益，总收益分别为661530.3万元和703603.6万元。博弈双方依据固定策略选择出口量时，总收益分别为679762.4万元和734437.6万元。另外，计算博弈方按实际产能进行决策时的总收益分别为630233.1万元和683388.5万元，作为参照，对比博弈方采取不同策略的总收益，绘制成图5。

表5-1　马来西亚和中国稀土产能(单位/十吨)

注：A表示马来西亚，B表示中国，AC表示实际产能(Actual Capacity)

表5-2　不同策略下马来西亚和中国的出口量(单位/十吨)

注：RS表示冒险策略(Risky Strategy)，CS表示保守策略(Conservative Strategy)，SS表示固定策略(Stationary Strategy)

图1　不同策略下博弈方的总收益

从图1中可以看出，当博弈双方的行动集合变化不确定时，马来西亚和中国采取冒险策略、保守策略或固定策略的总收益都大于按产能出口时的总收益，这说明文中给出的策略是可行的。图1中冒险策略和保守策略总收益基本相同，与理论分析的冒险策略与保守策略等价的结论一致，并且可以看出，博弈方采取固定策略时的总收益明显大于冒险策略和保守策略，说明文中构建的博弈运动模型和求解方法是合理、有效的。这可以为稀土出口贸易提供一些启示，出口国应该采取相对稳定的稀土出口量，可以构建稀土贸易平台、定期发布产能和出口信息，这些措施有利于稀土出口国获得更多的收益和避免恶性竞争。另外，当单个博弈方的行动集合变大、变小或者变化情形不确定时，可以看作是双方行动集合都发生变化的特殊情境，不再赘述。

5结语

本文首先分析了马来西亚的出口行动集合变化的博弈运动模型，发现均衡状态与经典的纳什均衡有很大的不同，在博弈运动模型中均衡状态是一个运动转移的过程。然后文章分析了博弈双方的稀土生产不稳定情形，探讨了博弈双方的行动集合都发生变化的博弈运动，给出稀土出口国应该采取相对稳定的出口量和发布的稀土产能等信息的应对措施，这对于稀土贸易出口国应对博弈对手行动集合变化的新情况具有指导意义。当然，本文只考虑了两个博弈方的稀土出口竞争，对多个博弈方的行动集合变化的博弈运动模型还要做进一步研究。

参考文献：

[1] Schwalbe U, Walker P. Zermelo and the early history of game theory[J]. Games and Economic Behavior, 2001, 34(09): 123-137.

[2]Neumann J V, Zur theorie der gesellschaftsspiele[J]. Mathematische Annalen, 1928, 100(1): 295-320.

[3]Von Neumann J, Morgenstern O. Theory of games and economic behavior(commemorative edition)[M]. Princeton university press, 2007.

[4]Nash J. Non-cooperative games[J]. The Annals of Mathematics, 1951, 54(2): 286-295.

[5]Smith J M, Price G R. The logic of animal conflict[J]. Nature, 1973, 246: 15.

[6]Tse P K. China’s rare-earth industry[M]. US Department of the Interior, US Geological Survey, 2011.

[7]王正明,张许静.稀土资源税对“寡头”国出口市场势力的影响研究[J].经济经纬,2012,2(2):52-55.

[8]裴文琳, 孔锐. 我国稀土进出口量与价格关联度状况分析[J].资源开发与市场, 2011, 7: 613-616.

[9]Elsadany A A. Competition analysis of a triopoly game with bounded rationality[J]. Chaos, Solitons & Fractals, 2012, 45(11): 1343-1348.

[10]Elsadany A A, Agiza H N, Elabbasy E M. Complex dynamics and chaos control of heterogeneous quadropoly game[J]. Applied Mathematics and Computation, 2013, 219(24): 11110-11118.

[11]卢亚丽.主从型Bertrand价格博弈模型及其动力学分析[J].系统工程,2012,30(002):91-94.

[12]闫安,达庆利,裴凤.多个企业同时博弈的动态古诺模型的长期产量解研究[J].管理工程学报,2013,(1):94-98.

[13]Mallard G. Modelling cognitively bounded rationality: an evaluative taxonomy[J]. Journal of Economic Surveys, 2012, 26(4): 674-704.

[14]廖萍康,张卫国,谢百帅,闫杜娟.相异成本和广义非线性需求下多寡头古诺模型及应用[J].运筹与管理,2013,22(2):172-179.

[15]Anufriev M, Kopányi D, Tuinstra J. Learning cycles in Bertrand competition with differentiated commodities and competing learning rules[J]. Journal of Economic Dynamics and Control, 2013, 37(12): 2562-2581.

[16]Zschocke M S, Mantin B, Jewkes E M. Mature or emerging markets: competitive duopoly investment decisions[J]. European Journal of Operational Research, 2013, 228(2): 612-622.